Shanghai University
Article Information
- Haoyuan GUO, Liyuan ZHANG, YajunYIN, Yongxin GAO. 2015.
- Relations between cubic equation, stress tensor decomposition, and von Mises yield criterion
- Appl. Math. Mech. -Engl. Ed., 36(10): 1359-1370
- http://dx.doi.org/10.1007/s10483-015-1988-9
Article History
- Received Oct.8,2014;
- Revised Mar.4,2015
2. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
3. Department of Mathematics, Tianjin University, Tianjin 300072, China
The well known von Mises yield criterion is widely used to predict the occurrence of plastic deformation of ductile metal materials,such as steel and aluminum[1, 2, 3].To derive this criterion,the stress state is always decomposed into two states,as shown in Fig. 1.One is named as the spherical stress state,and the other is the deviatoric state[4].This additive decomposition seems natural and was introduced insipidly in many textbooks of solid mechanics[5, 6, 7, 8, 9].However,when having a deeper understanding of it,we find that such a decomposition operation is of essential importance to the whole theoretical system of plastic mechanics.Following the above decomposition scheme,the key point of the problem can be caught successfully.
 |
| Fig. 1 DSDT,where σ1,σ2,and σ3 are three principal stresses,and σm is their average value |
Accordingly,one may encounter the following questions.In the mathematical field,where does the decomposition of spherical/deviatoric tensor (DSDT) come from?What is the relationship between the DSDT and the energy decoupling property?How is the DSDT introduced into the explorations of plastic phenomena?With the inspiration of Cardano's method for cubic scalar equation,we try to answer the above questions in this article and give a comprehensiveview on the relations of the cubic tensor equation,the DSDT,the energy decoupling,and the von Mises yield criterion.For the simplicity of statements,our discussion is limited to the field of small strain deformation.
2 Cardano's method for cubic scalar equationWe first give a brief review of Cardano's method for cubic scalar equation.This method is based on a two-step additive decomposition,which was proposed by Cardano in the 16th century[10, 11, 12].
The general form of a cubic scalar equation can be written as
The first step of Cardano's method is to eliminate the quadratic term in Eq.(1) by the variable substitution
Substituting Eq.(2) into Eq.(1) yields the standard form of the cubic scalar equation,that is, where 
In the second step,Eq.(3) is then transformed into a quadratic equation with another additive decomposition.The relation
produces z3=u3+v3+3uv(u+v),which is further converted to Comparing Eq.(5) with Eq.(3) leads to two equations:3uv+p=0 and u3+v3+q=0.Let U=u3 and V=v3.One has Equations (6) and (7) are further transformed into a quadratic equation,whose roots can be readily calculated using the standard formula.Then,the initial cubic scalar equation is finally solved.In the above two steps,we consider the first one to be of essential importance.Inspired by Cardano's method for the cubic scalar equation,we examine the additive decomposition of a tensor in the simplification of a cubic tensor equation in the next section.
3 Simplification of cubic tensor equation and DSDTIn most solid mechanics textbooks,the concept of the DSDT is introduced either in the section of the Cauchy stress or at the beginning of the plastic yield criterion.These introductions generally directly illustrate how to calculate this additive decomposition and how it produces the energy decoupling property.However,a clear mathematical origin of the DSDT is usually missed.To understand where the DSDT comes from,we refer to Cardano's method for the cubic scalar equation.In the pure mathematical field,we prove that the DSDT can be derived from the simplification of cubic tensor equation.
To generate a cubic tensor equation,we use the Caylay-Hamilton theorem,which is well applicable for tensor analysis[4]and matrix algebra problems[13, 14, 15].For a second-order tensor A in the three-dimensional Euclidean space,its characteristic polynomial is defined as
where det(·) denotes the determinant of a tensor,the scalar λ is the eigenvalue of A,and JA1,JA2,and JA3 are the first,second,and third principal invariants of A,respectively.All tensors discussed in this paper are assumed to be symmetric.Using the tensor A to replace the scalar λ in Eq.(8),one has the following characteristic tensor equation: where An A·A·· · ··A(n=1,2,3).Equation (9) is a cubic tensor equation with the variable of tensor A,which is regarded as the initial cubic tensor equation in our following analysis.
A·A·· · ··A(n=1,2,3).Equation (9) is a cubic tensor equation with the variable of tensor A,which is regarded as the initial cubic tensor equation in our following analysis.
To simplify Eq.(9),Cardano's method for the cubic scalar equation is used in a similar way.As mentioned above,the key point of Cardano's method is the elimination of the quadratic term using the first-step additive decomposition (see Eq.(2)).To eliminate the quadratic term of cubic tensor equation,an additive decomposition is proposed accordingly.
To start with,a general form of additive decomposition is expressed as
Commonly,A1 and A2 are not independent.Without loss of generality,we specify A1=f(A2),where the function f(·) can be either isotropic or anisotropic.It should be mentioned that unlike the scalar situation,the exact form of A1=f(A2) and the decomposition for tensor A are not easy to obtain.This is due to the significant difference between the complexity of the scalar and tensor functions.The details are as follows.For the cubic scalar equation (1),the first-step decomposition can be written as x=x1+x2 with a polynomial describing the relation between x1 and x2 as x1= .After a simple calculation,a unique decomposition is obtained as x1=k1x2−b/3,regardless of the value of k1(except k1=−1 producing constant x=−b/3).For the tensor equation,however,we cannot have such a series form of function without preconditions.The tensor series A1=f(A2)=
.After a simple calculation,a unique decomposition is obtained as x1=k1x2−b/3,regardless of the value of k1(except k1=−1 producing constant x=−b/3).For the tensor equation,however,we cannot have such a series form of function without preconditions.The tensor series A1=f(A2)= indicates the relation A1· A2=A2·A1,which does not always hold.In order toget the explicit form of tensor function f(A2) and complete the following derivation,we need an additional condition:the decomposition method is required to have the mathematically simplest form.With this condition,we finally determine that the simplest decomposition is just the DSDT.
indicates the relation A1· A2=A2·A1,which does not always hold.In order toget the explicit form of tensor function f(A2) and complete the following derivation,we need an additional condition:the decomposition method is required to have the mathematically simplest form.With this condition,we finally determine that the simplest decomposition is just the DSDT.
In this paper,we define the simplest form to be the least terms in the final explicit expression.Following this definition,an isotropic function is simpler than an anisotropic one,since it has fewer terms[4].The function f(·) is thus assumed to have the isotropic property,and A1=f(A2) is then written as[4]
where G is the metric tensor,and the coefficient kn (n=0,1,2) is a function of JA21,JA22,and JA23.Substituting Eqs.(10) and (11) into Eq.(9),we obtain a new equation with the variable A2.To keep its cubic order,the coefficient k2 in Eq.(11) must be zero.Then,the simplified substitution becomes
One readily calculates that the coefficient of the quadratic term in Eq.(12) equals 3k0(k1+1)2 − JA1(k1+1)2.With k1+1 ≠ 0 ensuring the cubic term non-zero,the quadratic term is eliminated only when k0=JA1/3.With this relation,we haveIt can be found that the arbitrary value of k1(≠ −1) makes no essential difference for the simplification in Eq.(13).For simplicity,we set k1 to be zero.In this special case,we finally get the explicit expressions of A1 and A2 as
which are exactly the same as the well-known definitions of the spherical and deviatoric tensors.In the above derivation,we introduce two conditions for the undetermined decomposition to be the DSDT.First,the tensor function A1=f(A2) is isotropic.Second,the coefficient of A2 in this function is zero.
As shown above,we provide a possible mathematical origin for the DSDT.Besides,we find that the DSDT can be derived as an extension of Cardano's method for the cubic scalar equation to the tensor case.
4 DSDT and energy decouplingThe DSDT is not only useful for equation simplification in mathematics but also has important applications in physics and mechanics.For example,if the variable in the tensor equation becomes the stress tensor in mechanics,the DSDT has a clear physical meaning,which is the decoupling of elastic deformation energy density under the conditions of general loading and small deformation[6, 7, 8].Actually,this conclusion is just a direct deduction of the simplified form of cubic tensor equation.To derive this property,we introduce the linear elastic constitutive relations,
where E and ν denote Young's modulus and Poisson's ratio,respectively.The DSDT requires the stress tensor σ to decompose into a spherical part σS and a deviatoric part σD.Similarly,the strain tensor ε is decomposed as ε=εS+εD,where εS=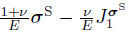 G and εD=
G and εD=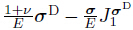 G are solved by the constitutive relations in Eq.(16).Then,the coupling term of the strain energy density is calculated as
where':'represents the double-inner product.With the relation σS:σD=
G are solved by the constitutive relations in Eq.(16).Then,the coupling term of the strain energy density is calculated as
where':'represents the double-inner product.With the relation σS:σD=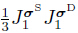 ,we finally get
,we finally get
To find the relation between the tensor equation and energy decoupling,the tensors A and A2 in Eqs.(9) and (12) are regarded to be σ and σD,respectively.Since the quadratic term in Eq.(12) is eliminated by the DSDT,JσD1 becomes zero according to the Caylay-Hamilton theorem.Therefore,the coupling energy wc in Eq.(18) is also zero,indicating that the mathematical simplification of cubic tensor equation induces the mechanical property of strain energy decoupling.
Furthermore,it should be noticed that the energy decoupling is not limited by the condition of linear elastic property.For arbitrary solids subjected to external forces,the stress σ and the strain rate  are generated.Decomposing σ and
are generated.Decomposing σ and  into the spherical and deviatoric parts,one has σ=σS+σD and
into the spherical and deviatoric parts,one has σ=σS+σD and  =
= .To analyze the coupling strain energy power density,for example,we only calculate the energy Wc done by the deviatoric stress on the spherical strain rate as follows:
.To analyze the coupling strain energy power density,for example,we only calculate the energy Wc done by the deviatoric stress on the spherical strain rate as follows:
Regard the deviatoric tensor σD to be A2 in the previous cubic tensor equation.Since the quadratic term has been eliminated,according to the Caylay-Hamilton theorem,one directly has
which shows that the coupling strain energy power density contributed by the deviatoric stress on the spherical strain rate is zero.Similarly,the coupling power density by the spherical stress on the deviatoric strain rate is also zero.These results indicate that the strain energy power density finally decouples into two parts,σD: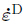 and σS:
and σS: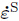 .
.
Note that the relation JσD1=0(or JA21=0) is very important for the above derivation,because it links the mathematical simplification and the mechanical energy decoupling property.After the DSDT process,the quadratic term is eliminated in the new cubic tensor equation (13).Then,the relation JA21=0 can be derived according to the Caylay-Hamilton theorem.Since the coupling energy is proportional to JσD1(or JA21),the conclusion can be drawn that the energy decouples with the elimination of quadratic term.
In most textbooks,the energy decoupling is introduced with the requirement of linear elastic property.Our above analysis is of more universal significance since it does not have to obey such strong constraint of material constitutive relation.Besides,our derivation mainly focuses on the energy power density rather than the energy density.Actually,the time integration of the energy power density can directly generate the energy density.When the deformation is small enough,the difference between the reference configuration and the current configuration can be ignored reasonably,and then the strain tensor is obtained via multiplying the strain rateby the time increment.In this case,the property of energy decoupling is immediately realized.In addition,it should be mentioned that in the large deformation case,one needs to consider more situations,e.g.,the configuration,the definition of strain tensor,and the constitutive relations,which are beyond the scope of this paper.
5 Simplest form and choice of natureEven for a deformed material with linear elastic property,the elastic strain energy is still proportional to a quadratic form of the generated stress (strain).It is amazing to see that the nonlinear quadratic energy density can be linearly decoupled by a simple additive decomposition.Therefore,the decoupling property is unusual and needs to be carefully explored.
Another question arises immediately.Since the DSDT ensures the energy decoupling property,can the condition of energy decoupling lead to the DSDT?Or,does there exist a one-to-one correspondence between the DSDT and the energy decoupling?Unfortunately,the answer is no.
One counter-example is given as follows.For simplicity,it is assumed that the deformed material has the linear elastic property,as expressed in Eq.(16).After decomposing σ linearly into σ1 and σ2,the decomposition of ε=ε1+ε2 can be obtained accordingly.The corresponding energy decoupling property is equal to the validation of two equations,σ2:ε1=0 and σ1:ε2=0.With the constitutive relation in Eq.(16),the above two equations are then transformed into
Equation (21) should keep its validation for arbitrary value of ν,which requires
The necessary and sufficient condition for Eq.(23) is either Jσ11=0 or Jσ21.Without loss of generality,we assume
It is clear that only with Eqs.(22) and (24),one cannot judge whether σ1 is the deviatoric part of the stress tensor σ,because the total number of available equations is less than the total number of the variables in the tensor.Similarly,whether σ2 is a spherical tensor or not cannot be determined.Thus,the scheme of the additive decomposition leading to the energy decoupling is not unique.This non-unique result is similar to the case of simplification of cubic tensor equation (Section 3).Countless schemes of additive decomposition can produce the decoupling property,if no condition is added.With a requirement of the simplest form,however,this problem can only be solved by a unique decomposition scheme,that is,the DSDT.
The derivation is somewhat similar to the proof for the tensor equation in Section 3.Assume that σ2 is a function of tensor σ1,where σ2=g(σ1).The function g(·) can be either anisotropic or isotropic.The isotropic property is chosen for g(·) for simplicity.As shown in Eq.(11),this isotropic function is expressed as
where tn (n=0,1,2) is the function of Jσ11,Jσ12,and Jσ13.Double-inner multiplying the tensor σ1 at both sides of Eq.(25) and using Eqs.(22) and (24),one has Obviously,the simplest solution of this equation is t1=t2=0.Therefore,the final expression of the tensor decomposition becomes σ2=t0G and σ1=σ − t0G.Using Eq.(24) again,t0 is determined as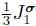 .Immediately,it is clear that the tensors σ1 and σ2 are just the deviatoric and spherical parts of the tenor σ,respectively.In mathematics,the above simplest form requires two conditions.First,the function σ2=g(σ1) is isotropic.Second,the coefficients of σ1 and σ21 in this function are zero.
.Immediately,it is clear that the tensors σ1 and σ2 are just the deviatoric and spherical parts of the tenor σ,respectively.In mathematics,the above simplest form requires two conditions.First,the function σ2=g(σ1) is isotropic.Second,the coefficients of σ1 and σ21 in this function are zero.
Summarizing the results of Sections 3,4,and 5,we can infer that the mathematical simplification and the mechanical energy decoupe complement each other.To simplify the cubic tensor equation,the additive decomposition is introduced with the inspiration of Cardano's method for the cubic scalar equation.However,the quadratic term in the tensor equation can be eliminated with countless schemes of additive decomposition.Besides,there also exist countless decomposition schemes that can decouple the elastic energy.If the condition of the simplest form is added,for both situations,a unique decomposition is remained,which is just the DSDT.Therefore,a one-to-one correspondence exists between the additive decomposition and energy decoupling when the requirement of the simplest mathematical form is only supplied.
For the mathematical form,this uniqueness of additive decomposition is very special.Does it possess a more significant physical meaning than other ordinary choices of decomposition?Fortunately,the answer is yes,since nature also obeys the minimalist principle.In other words,the mathematical simplicity of the DSDT is not only the choice of mankind,but also the choice of nature in some fields.The establishment of von Mises yield criterion is a good example to support these statements.
The von Mises yield criterion is one of the most important bases of plastic mechanics.During the demonstration of this criterion,the spherical/deviatoric stress decomposition plays an essential role[1, 2, 3].Learning from the history of mechanics,one knows that the starting point of von Mises yield criterion is the tensile-torsion test of thin-walled metal tube.In this test,it is found that the plastic deformation does not accompany any volume change.This special phenomenon has caught great attention of the researchers.They were acutely aware of a significant point that the volume strain and its related stress and energy probably have no contribution to the development of plastic deformation.Since the volume deformation is of no use,it should be removed from the plastic analysis using certain methods.
In the hydrostatic (or spherical) stress state,the volume changes while the shape remains unchanged.On the contrary,in the deviatoric situation,the shape is distorted while the volume remains unchanged.Since the volume change has nothing to do with the plastic deformation,the shape distortion should be the only decisive factor for plastic property.Therefore,the researchers (e.g.,von Mises,Hencky,and Huber et al.) tried to choose an additive decomposition to decompose the general stress state in order to eliminate the effect of volume change.On the basis of this result,they captured the key point for the establishment of von Mises yield criterion.
We can also analyze this problem from the energy viewpoint.Because of the energy decoupling property,the strain energy density is equal to a sum of the volume deformation energy density and the distortion energy density.Since the volume deformation energy density is independent of plastic deformation,the distortion energy becomes the only dominating one.As mentioned above,the energy decoupling condition alone (see Eqs.(22) and (23)) cannot determine the exact expression of the stress tensor decomposition.Naturally,one wants to select the simplest mathematical form,which just decomposes the initial stress tensor into the hydrostatic and deviatoric parts.Fortunately,this simple decomposition is also confirmed by the experiments:to the first approximation,a moderate hydrostatic pressure state cannot affect theplastic deformation[1].The consistency of the selections of human and nature shows that,sometimes,the simplicity is not only the choice of human but also the choice of nature.Although only the simplest decomposition is not enough to fully explain all mechanical phenomena,it indeed provides a useful way to have some deeper understandings of some mechanical behaviors.Finally,this mathematical simplest decomposition finds an important application in the field of physics and plastic mechanics.
It should be noticed that the conclusion at the beginning of this section (Eqs.(21) to (26)) can be directly used in the demonstration of von Mises yield criterion.The conclusion initially derived for the elastic problem is still valid here,because the von Mises yield criterion is for the critical transition between the elastic and plastic behaviors.
6 Discussion 6.1 Other application of DSDT in natureBesides the application in von Mises yield criterion,the physical phenomenon of the prime and secondary waves in the stress wave theory also stands for the significance of the DSDT.If the body force is neglected,the dynamics Lame-Navier equation can be written as
where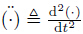 ,∇ denotes the gradient operator,G and λ are two material constants,and ρ is the density of the media.Operating both sides of Eq.(27) with the dot product of ∇,one has
where θ=∇·u,and c2p=
,∇ denotes the gradient operator,G and λ are two material constants,and ρ is the density of the media.Operating both sides of Eq.(27) with the dot product of ∇,one has
where θ=∇·u,and c2p=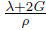 .The variable θ represents the spherical part of the strain tensor
.The variable θ represents the spherical part of the strain tensor 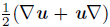 .Equation (28) is the control equation of the prime wave.After the spherical part is removed from the strain tensor in the initial Lame-Navier equation of Eq.(27),the equation of the secondary wave can be obtained in a similar way,where the deviatoric strain tensor dominates the wave propagation.Based on the above demonstration,two types of waves propagate in the elastic materials with different velocities.The longitudinal wave,also called the expansion wave and dominated by the spherical tensor,induces a volume change in the media.The transverse wave,also called the shear wave and dominated by the deviatoric tensor,induces a shape distortion without any volume change[5].Therefore,the DSDT also shows its physical power in the field of wave behavior.
6.2 No further decomposition for deviatoric tensors
.Equation (28) is the control equation of the prime wave.After the spherical part is removed from the strain tensor in the initial Lame-Navier equation of Eq.(27),the equation of the secondary wave can be obtained in a similar way,where the deviatoric strain tensor dominates the wave propagation.Based on the above demonstration,two types of waves propagate in the elastic materials with different velocities.The longitudinal wave,also called the expansion wave and dominated by the spherical tensor,induces a volume change in the media.The transverse wave,also called the shear wave and dominated by the deviatoric tensor,induces a shape distortion without any volume change[5].Therefore,the DSDT also shows its physical power in the field of wave behavior.
6.2 No further decomposition for deviatoric tensors
Cardano's method has two steps of additive decomposition,implying that the spherical/deviatoric tensors might have further decomposition.After clarifying the DSDT,it is natural to consider whether the tensor decomposition can go further or not.Obviously,the spherical tensor is the simplest form,and it cannot be decomposed any more.Therefore,is it possible to further simplify the deviatoric tensor by using a second-step additive decomposition?In Appendices A and B,we prove that no further additive decomposition can satisfy the basic physical requirement of the tensors generated from the decomposition to be real symmetric.Specifically,for the general stress state σ1 ≠ σ2 ≠ σ3,the decomposed tensors cannot have real value components.For the special case σ1=σ2 ≠ σ3,the symmetric requirement cannot be satisfied,where σ1,σ2,and σ3 denote three principal stresses of the tensor σ.In summary,the negative answer to this question indicates that the simplest elements obtained by the additive decomposition are indeed the spherical and deviatoric tensors.
7 ConclusionsIn history,Cardano's method has shown its power in solving the cubic scalar equation.Inspired by the scalar situation,we introduce an extended Cardano's method for the simplification of cubic tensor equation.Based on the theorems of tensor functions,we reveal an important scheme of tensor additive decomposition,that is,the DSDT.In the field of mathematics,choosing the DSDT makes the cubic tensor equation eliminate its quadratic term.For mechanics,it is found that the simplification of cubic tensor equation leads to the energy decoupling property.Cardano's method for the scalar case consists of two steps of additive decomposition.However,we prove that the second-step decomposition does not exist for the tensor case.Therefore,the simplest elements of the additive decomposition for tensor are indeed the spherical and deviatoric tensors.
Although the DSDT ensures the energy decoupling,it is not clear whether the energy decoupling can guarantee the additive decomposition to be the DSDT.We prove that the single condition of energy decoupling cannot determine the above case.When the requirement of the simplest form is added as another condition,the countless additive decomposition schemes degenerate to the unique DSDT.Thus,the relations between the DSDT and energy decoupling are uncovered from both sides.
For plastic problems,the von Mises yield criterion introduces the decomposition of spherical/deviatoric tensor as its first analysis step to capture the property of no volume change in plastic deformation.How this mathematical decomposition is extracted from mechanical behaviors deserves deeper consideration.Other than the reason that the DSDT makes a good prediction of plastic behavior,we suggest another potential explanation:the DSDT is the simplest form in the mathematical field with a validation by nature.
In summary,the decomposition of spherical/deviatoric tensor,the energy decoupling property,and the establishment of von Mises yield criterion are intrinsically and profoundly linked to each other.Our findings show that sometimes not only human beings but also nature prefer to simplicity.This result may bring inspiration to our scientific explorations:the paths for seeking simplicity and pursuing truth are consistent.
Acknowledgements Haoyang GUO and Liyuan ZHANG thank Prof.Xiqiao FENG and Dr.Zheng CHANG for providing useful guidance on this paper.The authors also thank the anonymous reviewers for the comments and suggestions to this work. Appendix A Proof of non-existence of further additive decomposition for deviatoric tensorIn Section 3,Eq.(12) is obtained with the elimination of its quadratic term.If we continue this problem following Cardano's method,the deviatoric tensor D might have a further additive decomposition,
Here,u and v are assumed to have the physical meaning of the stress (strain) tensor.We first give the conclusion:for a stress (strain) decomposition problem,there is no second-step additive decomposition.Namely,no real symmetric tensor of u or v can exist after a further decomposition.Its demonstration is as follows.
One of the key differences between a scalar quantity and a tensor is that whether the quantity satisfies the commutative law of multiplication or not.To utilize Cardano's method,the two tensors u and v in Eq.(A1) are required to satisfy the following relationship as the scalar does:
Under the condition (A2),Eq.(A1) is substituted into the tensor equation D3+JD2D−JD3G=0.Completely imitating Cardano's process in Section 2,a similar result is obtained after a continued utilization of the commutative law and the associative law,
where U=u3,V=v3,and α1 and α2 are constants with respect to JD2 and JD3,Since u and v have the mechanical property of stress or strain,their components should be real and symmetric.According to U=u3 and V=v3,the components and determinants of U and V should also have real values.
Denote the three principal stresses of tensor σ as σ1,σ2,and σ3,respectively.The non-zero principal invariants of deviatoric stress D are calculated as
Also,U and V have to satisfy the following equation:
With the relation W=U − V,one has
Since the determinants of both U and V are real values,the determinant of W2 must be nonnegative.To prove our conclusion that no further decomposition exists,according to the results of Eq.(A7),we introduce an intermediate variable Δ,that is,
Δ can also be expressed with the following principal invariants:

However,after substituting Eqs.(A4) and (A5) into Eq.(A8),we obtain an entirely contradictory result
The combination of Eqs.(A9) and (A10) shows that no matter under any coordinate system,the discriminant Δ is never larger than zero.However,according to the requirements of Δ in Eq.(A8),the discriminant Δ should be non-negative to give the decomposed tensors real eigenvalues.To satisfy both requirements of Eqs.(A8) and (A10),the only possible solution is Δ=0,indicating that at least two of the three principal invariants should be equal.Therefore,for the general stress state σ1 ≠ σ2 ≠ σ3,the principal invariants of U and V must be complex values since Δ < 0.Furthermore,all values of the determinants of U,V,u,and v are complex,which conflicts with the basic requirements that their determinants are real.
Therefore,for a general problem of physics,the deviatoric tensor is the final expression for the additive decomposition.
Actually,the above conclusion is consistent with that of the cubic scalar equation.Combining Eqs.(6) and (7) in Section 2,the discriminant Δs for the scalar equation is obtained as
The scalar equation has one real value root and one pair of complex value roots if Δs is positive.There are three different real value roots if Δs is negative.One pair of repeated real roots and another different real roots can be obtained if Δs is zero.It should be noticed that the roots mentioned here are the solutions of variable x in Eq.(1),but they are not the solutions of intermediate variables u and v.For the scalar equation whose roots are all real,the discriminant Δs must be non-positive.With the comparison of scalar equation,since the deviatoric tensor D has three real principle stresses,the discriminant Δ in Eq.(A10) is proved to be non-positive,too.Consistent again with the above conclusion of tensor u and v,scalars u and v cannot have three real value roots at the same time.Therefore,the situations for scalar and tensor equations are unified based on the hypothesis that the tensor product is exchangeable.In a special case,for example σ1=σ2 ≠ σ3 or σ2=σ3 ≠ σ1,the zero determinant offers tensor u or v a real value.However,further investigation shows that the tensor is not symmetric (see details in Appendix B).The non-symmetric property is a confliction with the basic requirement that the stress tensor should also be symmetric.Therefore,for a tensor with physical meaning,such as the stress or the strain tensor,the deviatoric tensor is the final and simplest form for the additive decomposition.
Appendix B Proof of non-existence of further additive decomposition when deviatoric tensor has two equal eigenvaluesWhen the three principle stresses are not all equal,a zero Δ is obtained and then both the tensors U and V have real value components.Hence,the deviatoric tensor D can be further decomposed with real value determinants.Without loss of generality,in the case σ1 = σ2 ≠ σ3,we strictly prove that meaningful decomposition does not exist,if the resulting tensor is required to be symmetric.In the Cartesian coordinate,a tensor can be written into a form of matrix after the base vectors are ignored.Then,the tensors P and D are expressed as
where the components of D on the diagonal line are 
With the assumption of σ1 = σ2 ≠ σ3,Eq.(A3) can be transformed into
If the tensors U and V are required to be symmetric,one can have unique solution with exclusion of the orthogonal similarity,that is,U=V= .In the principal coordinates,tensors U and V can be rewritten in a matrix form,
.In the principal coordinates,tensors U and V can be rewritten in a matrix form,
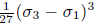 as the three main diagonal elements of tensors u and v.At the same time,by guaranteeing u+v=D,we have
where t=
as the three main diagonal elements of tensors u and v.At the same time,by guaranteeing u+v=D,we have
where t=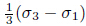 ,and i2=−1.
,and i2=−1.
Now via the orthogonal similarity transformation,the real component matrices u' and v' can be obtained.Although real value solutions with similarities are not unique,none of them is symmetric.For example,
This result conflicts with the common sense that the stress (strain) tensor always has a symmetry property.Thus,even in a special case σ1 = σ2 ≠ σ3,the decomposition of deviatoric tensor cannot meet the basic requirement.It implies that neither u nor v can be suitably taken as a stress or strain tensor.Although the additive decomposition exists mathematically,it still lacks physical meaning.
Summarizing the derivations in Appendices A and B,we know that,for the general stress state σ1 ≠ σ2 ≠ σ3,the decomposed tensor cannot have a real value.For the special case σ1 = σ2 ≠ σ2,the symmetric requirement cannot be satisfied.In other words,there does not exist physically meaningful decomposition for the deviatoric tensor.
| [1] | Hill, R. The Mathematical Theory of Plasticity, Oxford University Press, New York, 15-23(1998) |
| [2] | Xu, B. Y. and Liu X. S. Applied Elastic-Plastic Mechanics (in Chinese), Tsinghua University Press, Beijin, 88-97(1995) |
| [3] | Han, W. and Reddy, B. D. Plasticity:Mathematical Theory and Numerical Analysis, Springer, New York, 61-62(2012) |
| [4] | Huang, K. Z., Xue, M. D., and Lu, M. W. Tensor Analysis (in Chinese), Tsinghua University Press, Beijing, 101-102(2003) |
| [5] | Lu, M. W. and Luo, X. F. Basis of Elastic Theory (in Chinese), Tsinghua University Press, Beijing, 226-228(2001) |
| [6] | Fung, Y. C. Foundations of Solid Mechanics, Prentice-Hall, New Jersey, 80-81(1965) |
| [7] | Fung, Y. C. A First Course in Continuum Mechanics, Prentice-Hall, New Jersey, 99-101(1994) |
| [8] | Karasudhi, P. Foundations of Solid Mechanics, Kluwer Academic Publishers, The Netherlands, 59-61(1991) |
| [9] | Asaro, R. and Lubarda, V. Mechanics of Solids and Materials, Cambridge University Press, New York, 463-465(2006) |
| [10] | Guilbeau, L. The history of the solution of the cubic equation. Mathematics News Letter, 5, 8-12(1930) |
| [11] | Nickalls, R. W. D. A new approach to solving the cubic:Cardan's solution revealed. The Mathematical Gazette, 77, 354-359(1993) |
| [12] | Nahin, P. J. An imaginary tale:the story of √-1. Notices of the AMS, 46, 1233-1236(1998) |
| [13] | Atiyah, M. F. and MacDonald, I. G. Introduction to Commutative Algebra, Westview Press, New York, 27-30(1969) |
| [14] | Friedberg, S. H. and Insel, A. J. Linear Algebra, Prentice Hall, New Jersey, 258-259(2003) |
| [15] | Bhatia, R. Matrix Analysis, Springer-Verlag, New York, 7-9(1997) |
 2015, Vol. 36
2015, Vol. 36











































