Nomenclature

x, streamwise coordinate;	ρ, density;
y, normal coordinate;	μ, viscosity coefficient;
z, spanwise coordinate;	A, amplitude;
X, streamwise coordinate variation;	F, frequency;
Ma, Machnumber;	α, streamwise wavenumber;
u, streamwise velocity;	β, spanwise wavenumber;
v, normalvelocity;	c, phase speed;
w, spanwise velocity;	σ, growthrate.
T, temperature;

1 Introduction

With the improvement of computing power, the direct numerical simulation (DNS) is used to investigate the transition mechanism. In engineering, the practical transition method is the e-N method. The growth rate of the e-N method is provided by the linear stability theory (LST). A drawback of the LST is the parallel hypothesis. When non-parallelism is strong, the e-N method has limitations. Then, a new method calculating the growth rate which also considers non-parallelism and can make local stability analysis is required to replace the LST.

The local parallel hypothesis simplifies the initial boundary value problem of partial differential equation for the disturbances to an eigenvalue problem of ordinary differential equation. At large Reynolds numbers, the neutral curve predicted by the LST agrees the results of experiments. When the Reynolds number is small, it is different from the experimental results of Schubauer and Skramstad^[1]. The researches think that the difference is caused by nonparallelism. Gaster^{[2, 3]} took the increase of the boundary layer thickness as a small parameter and introduced it into the stability equations. He found the effect of the boundary layer thickness increasing on the growth rate. His results approached the experimental results of Barry and Ross^[4]. Yu and Zhou^[5] improved Gaster’s methods and got better results. Utilizing the method of multiple scales, Saric and Nayfeh^[6] obtained the higher order correction to the growth rate of disturbance. These results indicated the non-parallel effect on the stability, but these method could not be popularized and applied in practical engineering. Considering that the flow field is slowly varying in the streamwise direction, Herbert and Bertolotti^[7] and Herbert^[8] proposed the parabolized stability equations (PSEs) to predict the evolution of the disturbance. Chang et al.^[9], Zhang and Zhou^{[10, 11, 12]}, Dong et al.^[13], and Zhang and Su^[14] extended them to compressible flows. Zhou et al.^[15] investigated the non-parallel effect of flow stability using the PSE method. Because of the parabolic feature, the PSE needs an initial condition and marches downstream to be solved. It is not like the LST which can only perform a local stability analysis to give the amplitude growth rate of disturbances.

In engineering, a local stability analysis method considering non-parallelism is a better method than the LST or the PSE. The LST is a local method without non-parallelism. The PSE considers non-parallelism without locality. Therefore, we propose a new method called an expansion of the PSE method (the EPSE method), which contains characteristics of both locality and non-parallelism. While expanding the PSE in the streamwise direction, an eigenvalue problem can be obtained, which is only related to the local flow profiles and their streamwise derivatives. Therefore, the EPSE method can make local stability analysis like the LST. The results of the EPSE are checked by the DNS and the PSE in this paper.

In this paper, we first give the derivation process of the EPSE and introduce the application of the EPSE in the stability analysis and the mode change problem in a non-parallel boundary layer on a flat plate.

2 PSE

Consider the compressible flat plate boundary layer, where the coordinates x^*, y^*, and z^* stand for the streamwise, normal, and spanwise directions of the flow, respectively. The characteristic length is the boundary layer displacement thickness δ^*. The density, the velocity, the temperature, the pressure, and the viscosity are non-demensinalized by the infinity freestream ρ_∞^* , u_∞^*, T_∞^* , ρ_∞^*u_∞^*2 , and μ_∞^*, respectively. The Reynolds number is defined by Re = ρ_∞^*u_∞^*δ^*/μ_∞^*. The instantaneous variables can be expressed as

where φ = (ρ, u, v, w, T). When the instantaneous Navier-Stokes equation subtracts the steady equation, the disturbance equation is obtained. Neglecting the second-order and higher order disturbance terms, the linear disturbance equation is obtained. For convenience of deduction, the linear disturbance equation is expressed using the operator L, where ${\partial _t} = {\partial \over {\partial t}}, {\partial _x} = {\partial \over {\partial x}}, {\partial _y} = {\partial \over {\partial y}},$ and ${\partial _z} = {\partial \over {\partial z}}, $. where ${\hat \phi }$ is the disturbance shape function, and α, β, and ω are the streamwise wavenumber, the spanwise wavenumber, and the frequency, respectively. ${\hat \phi }$ and α are the slow variables of x. Substituting (2) into the disturbance equation (1) yields the stability equation The highest order of ${\hat \phi }$ with respect to x is the second derivative. Therefore, the operator L can be expressed as Because the flow is slow with respect to x, the terms about ∂_x² can be neglected. Then, the parabolized stability equation is obtained, If the first-order derivative terms are also neglected, the stability equation including the base flow streamwise derivation is obtained, which is called the extended O-S equation, If the base flow streamwise derivation in the operator L is neglected, the stability equation with parallel hypothesis is obtained, which is called the O-S equation. According to (3), there is

3 EPSE

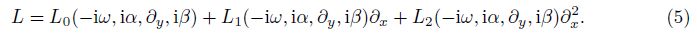
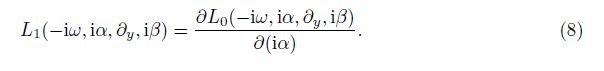
If the flow is slow on x, the basic flow and the disturbance can be expanded in the Taylor series in the vicinity of x₀. According to the parabolic principle, the second-order and the higher order are neglected. Substituting them to the PSE, the first-order expansion equations of the PSE are obtained. To see this, (4) is recasted as

Assume that x = x₀ + X, where X is a small variable. Expand the operators L₀, L₁ and the shape function ${\hat \phi }$ in the Taylor series, substitute them into (9), and neglect the terms including X² and higher order. The following equation can be obtained: According to the arbitrariness of X, there is which is the EPSE. It does not have the parabolic feature, and it is only related to the local velocity profiles and their streamwise derivatives. The EPSE and the homogeneous boundary condition constitute the eigenvalue problem. It can be used to perform the stability analysis. It reflects the non-parallel effect on the growth rate and the shape function, where A₀ stands for the amplitude at x₀. When the shape function ${\hat \phi }$₀(x₀, y) + ${\hat \phi }$₁(x₀, y)X is normalized, the disturbance is expressed as where Q(x) is the normalized coefficient, A₀Q(x)e^i(α(x₀)X) is the complex amplitude, and the change rate of the complex amplitude is The complex wavenumber is and the growth rate is where the subscript i implicates the imaginary part. It is observed that the growth rate is related to the normalized coefficient. The different normalized methods can obtain different growth rates. When the growth rates obtained by the different methods are compared, the normalized method must be consistent. Generally, the maximum of disturbance u is chosen to normalize the shape function. Especially, for the parallel flow, the normalized coefficient Q = 1, and there is σ = -α_i(x₀).

4 Application of EPSE in stability

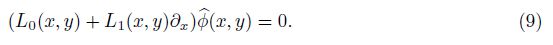
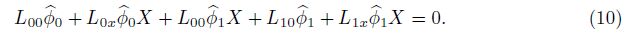
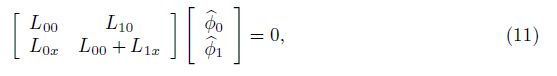
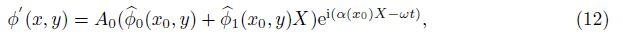
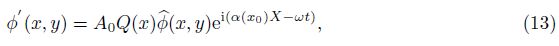
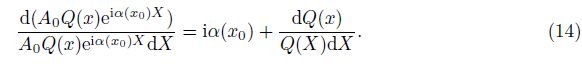
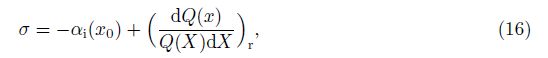
In order to verify the EPSE method, we give three applications: (i) the non-parallel effect on the stability; (ii) the non-parallel effect on the neutral curve; (iii) mode exchange caused by the dispersion relationship changing rapidly.

4.1 Non-parallel effect on stability

For investigating the suitability of the EPSE method, we analyze the stability in two cases, which are near the leading edge and far away from the leading edge, respectively. The Mach number is 4.5, the freestream temperature is 255.7 K, the freestream density is 0.736 kg/m³, and the viscosity coefficient is 1.628 × 10^-5 Pa·s. The non-dimensional frequency F is defined as

The computing parameters are given in Table 1.

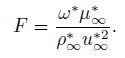
Table 2 shows the stability results of the LST, the PSE, and the EPSE at two different locations. When the location is far away from the leading edge x = 16.318 m, the wavenumber and the growth rate obtained from the three methods are comparable. The percentage difference between the results of the EPSE and the LST is 0.163%. Near the leading edge x = 0.514 m, the percentage difference between the results of the EPSE and the LST is 11.4%.

Figure 1(a) shows the amplitude evolution given by the DNS of Case 1, and it also shows the prediction results by the LST, the PSE, and the EPSE. Figure 1(b) gives the growth rate. It is indicated that when the location is far away from the leading edge, non-parallelism is weak, and the results of three prediction methods agree well with that of the DNS.

Figure 2 shows the results of Case 2. It is observed that the result of the EPSE approaches those of the PSE and the DNS, and it greatly differs from the result of the LST. It is indicated that when the location is near the leading edge, non-parallelism is strong, and the result of the EPSE is better than that of the LST. It reflects the non-parallelism effect on the growth rate.

According to the results, we know that far away from the leading edge, the EPSE considering non-parallelism has the same prediction results as the LST. Near the leading edge, it is better than the LST, and it approaches the PSE. Therefore, the EPSE can be used to do the stability analysis.

4.2 Non-parallel effect on neutral curve

For investigating the non-parallel effect on the neutral curve, we find that the normalized method can affect the growth rate. Generally, we use the maximum of disturbance u in the normal direction to normalize the shape function. In some cases, the disturbance u profiles have two peaks, and the maximum peak jumps from one peak to the other with the change of the location. Figure 3 shows the peaks of the disturbance u changing with the Reynolds number. Figure 3(a) shows the result of the first mode. It is observed that there are two peaks in the disturbance u profiles. With the Reynolds number increasing, the outside peak decreases. When the Reynolds number is Re < 9 100, the outside peak is larger than the inside peak. In the vicinity of Re = 9 100, both of the peaks are close to each other. When the Reynolds number is Re > 9 100, the inside peak exceeds the outside peak. The profile of the disturbance u of the second mode has the similar phenomena, as shown in Fig. 3(b).

If the maximum of the disturbance u is always used to normalize, the calculated growth rate jumps with the maximum peak location changing. Therefore, a reasonable normalized method is required. From the results of Fig. 3, it is found that when the length scale is nondimensionalized by the local boundary layer displacement thickness, the locations of the peaks are not changed with the Reynolds number. Therefore, we can use the value of the disturbance u of a certain location of peaks to normalize. Here, we use two peaks to normalize, respectively, and two neutral curves are obtained as shown in Fig. 4. Besides, the results of the LST are given. Figure 4(a) shows the first mode neutral curve. It is found that the neutral curve obtained by the EPSE is lifted. Neutral curves obtained by two normalized methods have some differences. The unstable range obtained by the outside peak is larger than that obtained by the inside peak. The critical Reynolds numbers obtained by the outside peak and the inside peak are Re = 7 300, 7 784, respectively. The critical Reynolds number predicted by the LST is Re = 8 147. It indicates that non-parallelism makes the critical Reynolds number in advance. Figure 4(b) shows the second mode neutral curve. It is found that there is little difference between two normalized methods. Compared to the result of the LST, the result of the EPSE is lifted slightly, and the critical Reynolds number is delayed.

4.3 Application in mode exchange

Generally, the effect of non-parallelism on stability is small for large Reynolds numbers. While there are some locations in the hypersonic boundary layer, non-parallelism has great effects on the disturbance dispersion relationship^{[16, 17]}. Thus, it affects the evolution of the disturbance. For this case, the prediction result by the LST may be not correct, and the prediction method must consider non-parallelism. Numerical examples are as follows.

The calculation parameters are chosen such that the Mach number is 7.0, the freestream temperature is 226.5 K, the freestream density is 1.843 kg/m³, the viscosity coefficient is 1.476×10^-5 Pa·s, and the Reynolds number is 2.0 × 10⁵. Figs. 5 and 6 show the phase speed c_r and the growth rate in different frequencies. It is found that there are two different modes. In the upstream, the smaller phase speed is called the slow mode (Mode S), and the larger one is called the fast mode (Mode F)^{[18, 19, 20]}. When they develop toward downstream, the phase speeds of slow and fast modes approach each other gradually. At the synchronization point, they are at their nearest proximity. Further downstream, they separate from each other. Before the synchronization point, the slow mode is the increasing mode, which is the first mode. After the synchronization point, according to the difference of frequencies, the slow mode may be the increasing mode called the second mode, and it may be the decreasing mode called the conjugated mode of the second mode. The fast mode is damped before the synchronization point. After the synchronization point, the development of the fast mode is contrary to that of the slow mode. For the higher frequency F = 8.0×10^-6, the slow mode evolves into the second mode, and the fast mode evolves into the conjugated mode of the second mode, as shown in Fig. 5. For the lower frequency F = 6.0 × 10^-6, the fast mode evolves into the second mode, and the slow mode evolves into the conjugated mode, as shown in Fig. 6.

The above results are based on the LST. Next, we give the evolution when disturbances go through the synchronization point using the DNS, the PSE, and the EPSE, respectively. Figure 7 shows the results of slow mode for F = 8.0×10^-6, and Fig. 8 shows the results of fast mode for F = 6.0 × 10^-6. The results of the LST indicate that the upstream modes link with the second mode after the synchronization point. It is observed that the disturbance evolution is consistent with the prediction result of the LST, but they do not agree well as shown in Figs. 7(a) and 8(a). However, the result of the EPSE is the same as that of the PSE, and it agrees well with the result of the DNS. The LST underestimates the growth rate in the vicinity of the synchronization point as shown in Figs. 7(b) and 8(b).

Figure 9 shows the evolution of fast mode for F = 8.0 × 10^-6, and Fig. 10 shows the result of slow mode for F = 6.0 × 10^-6. The results of the LST indicate that the upstream modes link with the damped conjugated mode after the synchronization point, while the results of the DNS indicate that the disturbance grows like the second mode when it goes through the the synchronization point. In this case, the results of the EPSE still agree well with those of the DNS and the PSE. It can be explained by the mode propagating in the non-parallel flow. When the mode propagates in the non-parallel flow, the upstream shape function deviates from the local shape function, and it projects to the local shape function. This is the scattering effect caused by non-parallelism. In the vicinity of the synchronization point, the dispersion relationships of two modes are close. The scattering effect makes one mode energy transfer to another. The weight of projecting to the second mode grows by its own instability.

It is found that the disturbance evolution is sensitive to non-parallelism in some situations. The prediction result of the LST may be incorrect, while the result of the EPSE considering non-parallelism is consistent with that of the DNS.

5 Conclusions

In this paper, a stability analysis method considering non-parallelism is proposed, which is called the EPSE method. Compared with the LST and the PSE, the EPSE has the characteristics of considering non-parallelism and making local stability analysis. Therefore, the EPSE is not like the PSE requiring the initial condition to march downstream, and it can do stability analysis like the LST at the local location.

When the EPSE method is used for leading edge stability analysis, calculating neutral curves, and mode exchange problems, the results agree well with those of the PSE and the DNS. Combining the EPSE and the e-N method, a new transition prediction method falling in between the LST and the PSE is formed, which contains characteristics of both. It is also found that the growth rate is related to the normalized method in the non-parallel flow. When the results obtained by different methods are compared, the normalized method must be consistent.