Shanghai University
Article Information
- R. ALASSAR. 2016.
- Fully developed forced convection through semi-elliptic ducts
- Appl. Math. Mech. -Engl. Ed., 37(1): 37-44
- http://dx.doi.org/10.1007/s10483-016-2020-9
Article History
- Received Mar. 11, 2015;
- in final form Jul. 7, 2015
Ducts are used in numerous industrial applications such as connecting devices,biochemical reaction chambers,physical particle separation,inkjet print heads,infrared detectors,diode lasers,and cooling computer chips. Industrial techniques produce channels of several cross-sections. In addition to the classical circular cross-sections,non-circular channels such as rectangular,elliptic,and trapezoidal,which have wide practical applications in micro-electromechanical systems (MEMS)[1, 2],are also produced. The third most common microchannel geometry may be the semi-circular profile,which occurs naturally in hard micromachining with isotropic etching[3, 4]. The semi-circular microchannels that are fabricated using hard or soft micromachining have,in fact,semi-elliptic cross-sections instead. In several cases,the axis ratio of such semi-elliptic sections is far from unity.
Several attempts have been made to solve the problem of flow and heat transfer in semicircular ducts. These studies are relevant to our problem since they stand as the limiting case when the axis ratio of a semi-elliptic channel approaches unity. Date[5] numerically solved the problem of fully-developed,laminar and turbulent,uniform-property flow in a tube containing a twisted-tape. Hong and Bergles[6] numerically investigated the laminar flow heat transfer in the entrance region of a semi-circular tube with the uniform heat flux. Two different thermal boundary conditions were considered. The first was the axially constant heat flux and uniform wall temperature around the entire semi-circular tube at each axial location,while the second was the axially constant heat flux and uniform wall temperature around the semi-circular portion and an insulated wall at the flat portion. Other relevant studies include those by Shah and London[7],Manglik and Bergles[8],and Sparrow and Haji-Sheikh[9].
Moreover,as the axis ratio tends to zero,a semi-elliptic channel degenerates to an infinitesimally narrow lenticular passage. The degenerate semi-elliptic channel is also a degenerate full elliptic channel. We refer to two important studies that deal with fully developed convection in elliptic channels,namely,those by Tao[10] and Bhatti[11],which are compared with the present results. Fully developed forced convection in ducts of semi-elliptic cross section was numerically studied by Velusamy et al.[12] who used a control volume-based procedure. Both the isothermal and uniform axial heat flux conditions on the duct walls were considered. With the availability of the exact velocity profile in a semi-elliptic channel provided recently by Alassar and Abushoshah[13] and Wang[14],we believe that an exact solution for the case of constant axial heat flux,numerically treated by Velusamy et al.[12],is possible.
In this paper,an exact solution of the problem of fully developed forced convection through semi-elliptic ducts,under constant axial heat flux and peripherally uniform temperature,is obtained. The solution is validated by comparing the local and average Nusselt numbers with the published approximate and asymptotic values.
2 Problem statement and solutionConsider a channel having a semi-elliptic cross-sectional area with the base length 2a,the height b,and the focal distance c ($c=\sqrt{{{a}^{2}}-{{b}^{2}}}$) (see Fig. 1). We assume thermally and hydrodynamically fully developed steady laminar forced convection. We also assume that a constant axial heat flux per unit area q is applied through the wall.The problem is hosted well in the elliptic cylindrical coordinates system (ξ,θ,z),whose transformation equations are
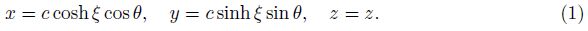
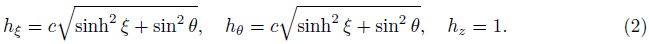
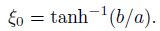

|
| Fig. 1 Problem configuration |
The governing equations of the problem under consideration are given in the elliptic cylindrical coordinates as
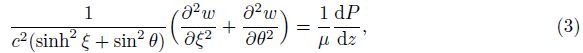
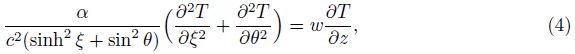
Under the constant axial heat flux,a simple energy balance over a segment of the duct of length dz shows[15] that
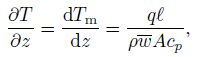
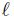 is the perimeter,and cp is the specific heat capacity. The mean temperature is defined as
is the perimeter,and cp is the specific heat capacity. The mean temperature is defined as



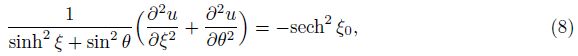
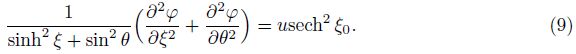
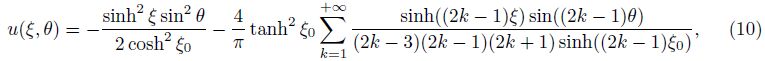
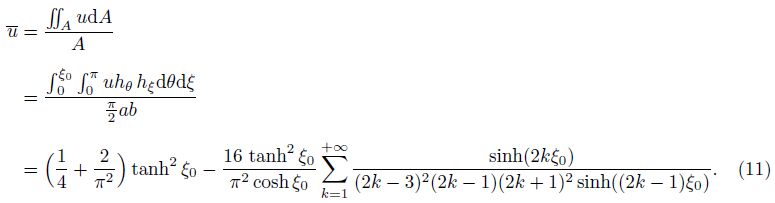
Using Eq. (10),Eq. (9) may now be rewritten as
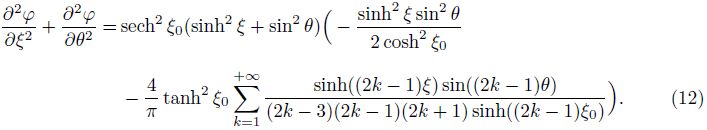
An obvious particular solution corresponding to the first term on the right-hand side of Eq. (12) is $-\frac{1}{24}$ sech4 ξ0 sinh4 ξ sin4 θ. To determine a particular solution of the second term on the right-hand side,we note that the product (sinh2 ξ+sin2 θ) sinh((2k−1)ξ) sin((2k−1)θ) can be expanded into sums of terms of the form sinh(iξ) sin(jθ). Observing that to each of these terms,a corresponding particular solution assumes the form sinh(iξ) sin(jθ)/(i2 − j2),where i ≠ j. In other words,
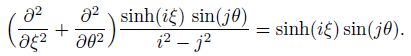
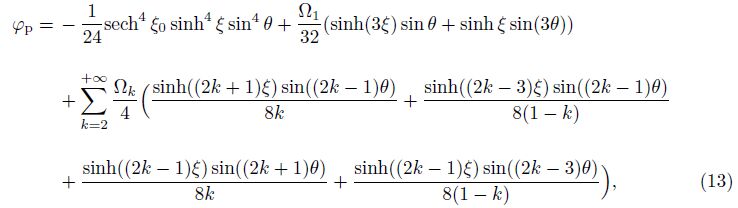
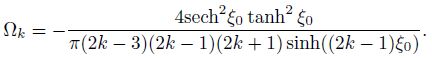
The symmetry of the problem at θ = π/2 and the conditions at θ = 0 and ξ = 0 make it necessary to assume a general solution in the form of
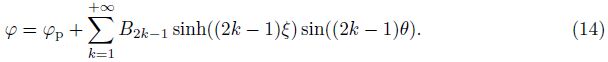
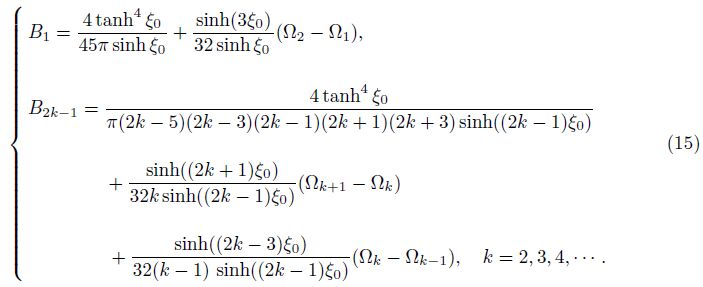

|
| Fig. 2 Temperature distribution for case b/a = 1/2 |
The dimensionless local Nusselt number is defined as
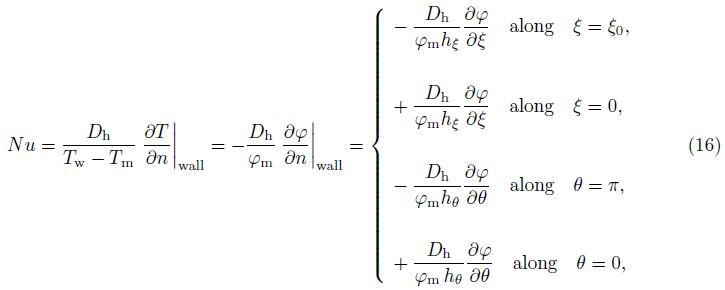
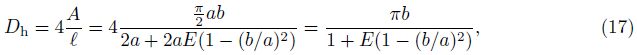
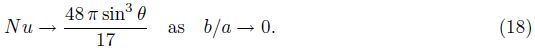
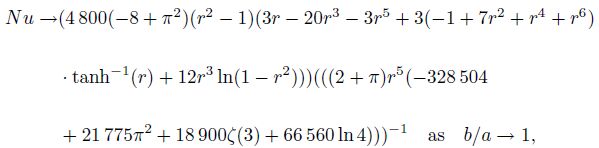

|
| Fig. 3 Local Nusselt number on flat bottom wall |
Figure 4 shows the local Nusselt number distribution on the curved wall. As b/a → 0,the curved and the flat surfaces coincide,and the same local Nusselt number distribution is expected. As b/a → 1,however,the Nusselt number can be shown to follow the distribution
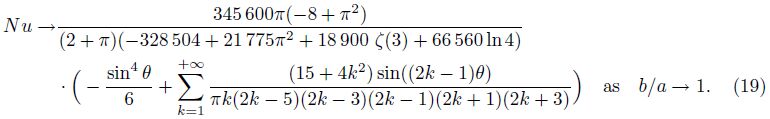

|
| Fig. 4 Local Nusselt number on curved wall |
Figure 4 shows that there are two symmetrical meeting points along the elliptic wall with the Nusselt number independent of b/a. These points are at the inflection of the Nusselt number curves and can be shown to occur at $\theta ={{\cos }^{-1}}\left( \mp \frac{1}{\sqrt{3}} \right)$. Figure 3,although not quite visible,also exhibits the same behavior.
Finally,we calculate the average Nusselt number,Nu,by averaging the local Nusselt number over the perimeter of the channel. It is easy to show that Nu may be given by the expression

Figure 5 shows the variation of Nu with the axis ratio. The two limiting values,namely,as the axis ratio tends to zero and as the axis ratio tends to 1,are $\frac{9{{\pi }^{2}}}{17}$ and $\frac{43200{{\left( {{\pi }^{2}}-8 \right)}^{2}}}{{{\left( 2+\pi \right)}^{2}}\left( -328504+21775{{\pi }^{2}}+18900\zeta \left( 3 \right)+66560\ln 4 \right)}$ ,respectively. These two results are usually reported in the literature as the approximate values of 5.225 and 4.088,respectively. The first,$\frac{9{{\pi }^{2}}}{17}$ ,was obtained by Tao[10] as a limiting value for a degenerate full ellipse. Of course,a degenerate full ellipse is identical to a degenerate semi-ellipse. We obtain the same value $\frac{9{{\pi }^{2}}}{17}$ by observing that as b/a → 0 (or equivalently ξ0 → 0),the curved top wall coincides with the bottom flat wall. One can then average the local Nusselt number given by Eq. (18) over the curved surface and then take the limit as ξ0 → 0,i.e.,
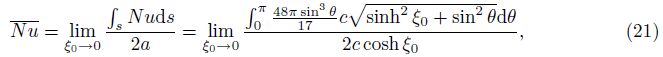

|
| Fig. 5 Average Nusselt number |
Table 1 compares the present exact values of Nu with those approximate values obtained numerically by Velusamy et al.[12] and few others.
| [1] | Wang G. J., Hsueh, C. C., Hsu, S. H., and Hung, H. S. Fabrication of PLGA microvessel scaffolds with circular microchannels using soft lithography. Journal of Micromechanics and Microengineering, 17, 2000-2005(2007) |
| [2] | Ziaie, B., Baldi, A., Lei, M., Gu, Y., and Siegel, R. A. Hard and soft micromachining for BioMEMS:review of techniques and examples of applications in microfluidics and drug delivery. Advanced Drug Delivery Reviews, 56, 145-172(2004) |
| [3] | Wang, C. Y., Liu, Y. H., and Chang, C. C. Analytical solution of electro-osmotic flow in a semicircular microchannel. Physics of Fluids, 20, 063105(2008) |
| [4] | Duan, Z. and Muzychka, Y. S. Slip flow in non-circular microchannels. Microfluid Nanofluid, 3, 473-484(2007) |
| [5] | Date, A. W. Prediction of fully-developed flow in a tube containing a twisted-tape. International Journal of Heat and Mass Transfer, 17, 845-859(1974) |
| [6] | Hong, S. W. and Bergles, A. E. Laminar flow heat transfer in the entrance region of semi-circular ducts with uniform heat flux. International Journal of Heat and Mass Transfer, 19, 123-124(1976) |
| [7] | Shah, R. K. and London, A. L. Laminar Flow Forced Convection in Ducts, Academic Press, New York (1978) |
| [8] | Manglik, R. M. and Bergles, A. E. Laminar flow heat transfer in a semi-circular duct with uniform wall temperature. International Journal of Heat and Mass Transfer, 31, 625-636(1988) |
| [9] | Sparrow, E. M. and Haji-Sheikh, A. Flow and heat transfer in ducts of arbitrary shape with arbitrary thermal boundary conditions. Jounal of Heat Transfer, 88, 351-357(1966) |
| [10] | Tao, L. N. On some laminar forced convection problems. Journal of Heat Transfer, 83, 466-473(1961) |
| [11] | Bhatti, M. S. Heat transfer in the fully developed region of elliptical ducts with uniform wall heat flux. Journal of Heat Transfer, 106, 895-898(1984) |
| [12] | Velusamy, K., Garg, V. K., and Vaidyanthan, G. Fully developed flow and heat transfer in semielliptical ducts. International Journal of Heat and Fluid Flow, 16, 145-152(1995) |
| [13] | Alassar, R. S. and Abushoshah, M. Hagen-Poiseuille flow in semi-elliptic microchannels. Journal of Fluids Engineering, 134, 124502(2012) |
| [14] | Wang, C. Y. On viscous flow in semi-elliptic ducts. Journal of Fluids Engineering, 137, 114502(2015) |
| [15] | Kays, W. M. and Crawford, M. E. Convective Heat and Mass Transfer, McGraw-Hill, New York (1993) |
 2016, Vol. 37
2016, Vol. 37



