Shanghai University
Article Information
- Jiangping HU, Bofu WANG, Dejun SUN. 2016.
- Numerical investigation of viscous fingering in Hele-Shaw cell with spatially periodic variation of depth
- Appl. Math. Mech. -Engl. Ed., 37(1): 45-58
- http://dx.doi.org/10.1007/s10483-016-2017-9
Article History
- Received Mar. 25, 2015;
- in final form Jun. 17, 2015
2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430071, China
When one fluid of low viscosity displaces another of high viscosity in a porous medium or a Hele-Shaw cell,the interface between the two fluids is unstable and will lead to the formation of finger-like pattern. This interface instability is called viscous fingering or Saffman-Taylor instability which is attributed to the remarkable work done by Saffman and Taylor[1]. The original motivation for studying this instability lies in the secondary oil recovery from the porous medium,and it is the petroleum engineers who first introduced the term viscous fingering in the experimental investigation of the displacement of oil by water from packs of granular material[2]. This interfacial instability has been studied in great detail from different points of view for more than sixty years since then. Physicists are attracted by its close relation to a wide range of phenomena,such as the dendritic crystal growth,directional solidification,diffusionlimited aggregation,electrochemical growth[3],the printer’s and ribbing instabilities[4, 5, 6],the dynamics of fractures[7],the Darrieus-Landau instability of flame fronts[8],the growth of bacterial colonies[9],filtration combustion[10],and void electromigration[11]. In mathematics,the Hele-Shaw problem is a relatively simple and sometimes solvable free-boundary problem. Thus, viscous fingering is regarded as a paradigm of morphological instability leading to interfacial pattern formation.
Since most porous materials are opaque,which brings many difficulties for observations when performing experiments on oil reservoirs,quite a few experiments were carried out in a Hele- Shaw cell[12] formed by two parallel plane plates with a gap between them. Generally,there are three geometries of the Hele-Shaw cell[13]: the rectangular Hele-Shaw cell,the radial Hele-Shaw cell,and the five-spot Hele-Shaw cell. In this paper,we only deal with the rectangular one with modification of one plate,as shown in Fig. 1. The fluids flow in the direction (the x-direction in Fig. 1) along the length of the cell. The length is denoted by L,the width by W,and the depth by b. It should have L >> W >> b. The depth-averaged equations that describe the flow in a Hele-Shaw cell are


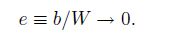
$\bar U$ and $\bar P$ represent the averaged velocity and pressure,respectively,and μ is the viscosity of the fluid. Taking b2/12 as the permeability of the porous medium,the flow satisfies Darcy’s law. Thus,the flow in a Hele-Shaw cell is analogous to the two-dimensional incompressible flow in porous media. There are plenty of theoretical and numerical studies based on the depthaveraged equations,and the depth b in experiments or simulations is regarded as a constant, but for the corresponding permeability of the porous medium,it should be variable.

|
| Fig. 1 Schematic of Hele-Shaw cells |
Ben-Jacob et al.[14] firstly introduced anisotropy in a modified radial Hele-Shaw cell by engraving a lattice on one of the plates and demonstrated the formation of dendritic pattern with anisotropy. Inspired by their experiments,many follow-up experiments with anisotropy have been performed,and various flow patterns that were never observed in the classical Saffman- Taylor instability have been reported. Rabaud et al.[15] once engraved a thin groove in the middle of each plate and stretched a thread from one end of the cell to the other. When the groove or the thread lay in the middle of the cell,the shape of finger they got was very well fitted by the analytical solutions of Saffman and Taylor[1] with the exception of a slightly sharper fingertip. The groove had a triangular profile and was of the scale of the gap of the cell. This local heterogeneity around the fingertip resulted in a sharper fingertip. When the thread was purposefully placed far from the center line of the cell,an asymmetrical finger could be obtained. McCloud and Maher[16] reviewed a wide variety of experiments that added perturbations or nonuniformity to the classical Saffman-Taylor problem including those mentioned above. The story of viscous fingering in the Hele-Shaw cell with heterogeneity continued. Recently,Al- Housseiny et al.[17] conducted a series of experiments of the two-fluid displacement in a Hele- Shaw cell with a small depth gradient along the flow direction. Fingering in a cell with positive gradient was inhibited provided that the invading less viscous fluid was wetting and the capillary number was below a critical value. In the cell with negative gradient,the finger could be triggered for wetting silicon oil displacing non-wetting water at a low capillary number.
In the experiments of two-phase displacement flow in the tubes with partially centered occlusion,de Lózar et al.[18] found new families of asymmetrical fingers localized in the leastconstricted regions of cross section. With the same geometry,Pailha et al.[19] captured the oscillatory propagation finger at relatively low capillary numbers,where the finger propagated at a constant speed with one edge exhibiting spatial oscillatory sideways motion of its interface behind fingertip. They proposed a surface tension-based mechanism for the oscillations. As one edge of the finger passed over the edge of the obstacle,there was a sudden decrease in the local transverse curvature because of the increased vertical space. This decrease in the curvature induced a local increase in the pressure,which drove the expanding interface moving sideways towards the sidewall of the cell,until it was constrained by the sidewalls. Though many experiments have been conducted to explore the finger patterns in unconventional Hele-Shaw cells,there is less numerical simulation on this. Thompson et al.[20] performed the numerical simulation of air into a wide fluid-filled cell with a smoothed step-like occlusion based on the depth-averaged model to reproduce all the finger modes observed experimentally and revealed new modes for symmetric finger propagation. They found that the oscillations occur only when the edges of the finger are close to and parallel to the edge of the obstacle and only when the transverse curvature is included,which confirms the surface tension-driven mechanism proposed by Pailha et al.[19].
In this work,the viscous fingering in a modified Hele-Shaw cell with spatially periodic variation of depth is numerically investigated by performing the three-dimensional simulation dealing with the full version of the Navier-Stokes equations directly using OpenFOAM. For the modified Hele-Shaw cell we present below,the depth varies continuously,and the depth gradient changes its direction only at the maximum and minimum depthes. This would induce the critical changes in the transverse curvature. Besides,the number of the maximum and minimum depthes is related to the wavenumber of depth perturbation,and this would bring more richness to the finger patterns. The remainder of the paper is organized as follows. The modified Hele-Shaw cell is introduced in Section 2,together with a brief introduction of the present numerical method. In Section 3,the results are presented,followed by the summary in Section 4.
2 Mathematical model and numerical methodThe modified Hele-Shaw cell with spatially periodic variation of depth is obtained by changing one of the plates with a non-flat one which allows the sinusoidal perturbation along the lateral (y) direction (see Fig. 1(b)). Thus,the depth b can be written as
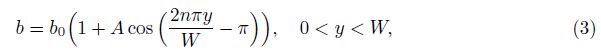
We use the solver interFoam of the open source CFD toolbox—OpenFOAM to perform our simulations. The multiphase flow solver,interFoam,used for two incompressible,isothermal immiscible fluids,is based on a modified volume of fluid (VOF) approach,which incorporates an interfacial compression flux term to mitigate the effects of numerical smearing of the interface. Different from the previous numerical simulation based on the depth-averaged equations[21, 22, 23], interFoam deals with the full version of the Navier-Stokes equations directly by the finite volume discretization on collocated grids. The two immiscible fluids are considered as one effective fluid throughout the domain,of which the physical properties are calculated as weighted averages based on the distribution of the liquid volume fraction,




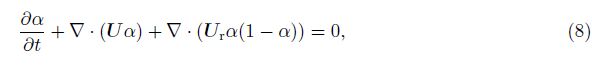
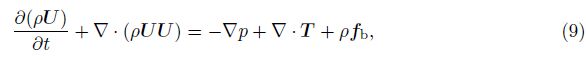
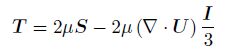
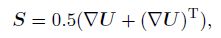
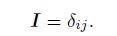


The relative velocity
Ur = U1 - U2
is designated as the compression velocity. From (8),only the value of Ur on the grid cell faces will be needed,and for the discretization,the compression term is determined from the gradient of phase fraction
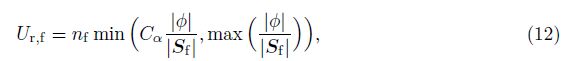


The algorithm used for the governing equations is based on the PIMPLE method which combines the algorithms SIMPLE and PISO. PIMPLE uses two loops. The inner one which takes several corrections for the pressure equations is performed to update pressure and velocity as PISO usually does. The other one is the outer corrector,which further ensures convergence. Deshpande et al.[25] performed a thorough investigation of the solver performance and concluded that the algorithm of interFoam ensures a consistent formulation of pressure and surface tension, and the curvatures computed by the solver converge to a value very close to the analytical one.
In the present simulation,the Hele-Shaw cell is assumed to be horizontal. Therefore,the effect of gravity can be ignored. The prescribed boundary conditions are such that the fluid can only enter and leave the channel through the inlet and outlet along the x-direction,respectively. The constant velocity condition is applied to the inlet boundary,and the outflow condition is applied to the outlet boundary. The top and bottom boundary conditions are naturally wall boundary conditions. The slip boundary conditions are applied to the sidewall boundaries, as suggested by Bensimon et al.[26]. To speed up the development of fingering,we impose a sinusoidal perturbation on the initially flat interface,
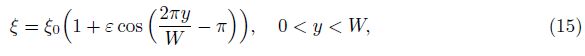


|
| Fig. 2 Comparison of numerical simulation (solid line) with analytical solutions (square) given by Pitts[27] in conventional Hele-Shaw cell,where relative width of finger is approximately 0.642 and results fit very well |
Then,the relative width λ of viscous finger as a function of the parameter 1/B∗ is examined and compared with the previous theory and experiments,as shown in Fig. 3. The parameter 1/B∗ is defined as
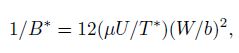

|
| Fig. 3 Relative size λ of finger as function of parameter 1/B ∗ |
The numerical simulation is conducted in a cell of size W =30 cm,b=2.54 cm,and b0 = 0.08 cm with the sinusoidal perturbation in depth. Attention is mainly focused on finger patterns at perturbation numbers n = 1,2,3,4,and the width of viscous fingering is also calculated. The effects of the ratio of the perturbation amplitude to the average depth A and the capillary number C are examined.
3.1 Fingering patternsFor n = 1 and A = 0.3,when the cell geometry is symmetric about the vertical center plane, a symmetric finger is obtained at C = 0.229×10-1,as shown in Fig. 4(a). The gray part located on the left of Fig. 4(a) shows the cross section of the cell in the yz-plane. The distribution of the pressure field is also symmetric,as shown in Fig. 4(b). The air pressure inside the finger is nearly constant. The oil pressure increases on passing along the interface from the fingertip,and the oil pressure gradient is uniform except for the area around the fingertip. However,when the cell geometry is asymmetric,an asymmetric finger can be obtained at the same displacement velocity,as shown in Fig. 4(c). The distribution of the pressure field of the asymmetric finger pattern is also asymmetric,as shown in Fig. 4(d). For both distributions of the pressure field, the oil pressure in the area ahead of the fingertip is lower than the air pressure,and the pressure in the area behind the fingertip is slightly higher than the air pressure. This pressure difference drives the viscous finger moving forward. Figure 5 shows that the finger propagates at the same constant velocity for both types of fingers. It means that the pressure difference across the interface is balanced by the surface tension. Therefore,the pressure difference attributed to the surface tension must decrease on passing along the interface from the fingertip towards the parallel portion. The symmetry of the cell about the vertical center plane does not affect the finger advancing velocity.

|
| Fig. 4 Finger patterns at C = 0.229 × 10 -1 for n = 1 |
For n = 2 and A = 0.3,we obtain four different fingering modes under different capillary numbers,as shown in Fig. 6. At a very low capillary number (C = 5.947×10-4),air is symmetric about the vertical center plane of the cell and occupies the entire width of the cell,as shown in Fig. 6(a). The double-tipped feature may attribute to the shape of the cross section. In the present cross section,there are two expanded regions. As the capillary number increases,when the finger forms,it tends to propagate in one of the regions. Then,the finger will propagate asymmetrically,as shown in Fig. 6(b)-6(d). At a low capillary number C = 9.974 × 10-3, one edge of the finger exhibits spacial oscillatory sideways motion behind its tip,as shown in Fig. 6(b). The figure also shows the contour of pressure distribution. The air pressure is now a little higher than the oil pressure out of the oscillation interface. For a higher capillary number (C = 2.394 × 10-2),the finger still propagates asymmetrically but without oscillation. Pailha et al.[19] also captured the oscillation propagation finger,and they ascribed this to the sudden decrease in the transverse curvature. However,in the present cell,the depth varies continuously, and so does the transverse curvature. From the fingertip,the interface moves sideways towards the wall,and the finger width increases. When the interface passes the minimum depth,the transverse curvature turns to decrease,and then the pressure difference across the interface cannot be balanced by the pressure difference provided by the surface tension. Thus,the interface is driven to move sideways towards the wall by air,and this movement increases the local oil pressure until the pressure difference between the two fluids is rebalanced by the surface tension. Then,the interface bulges locally. For the region around the bulge,the induced increase of the oil pressure drives the interface moving sideways against the wall until the pressure is balanced. The spacial oscillation is then formed by the alternating sideways movements,as shown in Fig. 6(b). At C = 2.394×10-2,the finger is narrower than that of C = 9.974×10-3. Though the interface passes the minimum depth,and the transverse curvature decreases,the decrease is not sufficient to drive the interface to move. Thus,the pressure difference across the interface is still balanced,and no oscillation occurs on the edge of finger. As the capillary number increases (C = 2.177 × 10-1),the finger continues narrowing,and the two edges of finger can be both contained in one of the expanded regions. Then,there is a shift from a wide finger to a narrow one,as shown in Fig. 6(d). Finally,the asymmetric finger propagates in one of the expanded regions of the cell.

|
| Fig. 5 Location of fingertip versus time at C = 0.229 × 10 -1 for both symmetric (square) and asymmetric (circle) fingers,together with linear fitting lines (solid lines),which shows that fingertips propagate at same constant speed |

|
| Fig. 6 Finger patterns of n = 2 and A = 0.3 |
For n = 3 and A = 0.3,several typical patterns at different capillary numbers are shown in Fig. 7. At a very low capillary number (C = 5.947 × 10-4),air occupies the entire width of the cell and is symmetric about the vertical center plane of the cell but with triple-tipped feature (see Fig. 7(a)). As the capillary number increases (C = 3.687 × 10-3),the decrease of the transverse curvature induces the movement of the interface towards the sidewall. Until the interface reaches one of the minimum depths,the pressure difference is not balanced. Therefore, the interface continues to move sideways. When it reaches one of the minimum depths,the induced increase in the oil pressure balances the pressure across the interface. Finally,the interface is bounded by the two central minimum depths (see Fig. 7(b)). As the capillary number increases (C = 8.820 × 10-3),oscillation occurs on two edges of the finger,and the pressure difference drives the interface moving further sideways until constrained by the sidewalls. Thus, a symmetric finger with two-edge oscillation forms (see Fig. 7(c)). As the capillary number increases further (C = 1.616 × 10-2),the strength of the oscillation is reduced,the distance between the fingertip and the first place where oscillation emerges after fingertip is lengthened, and the amplitude of the oscillation is diminished (see Fig. 7(d)). The oscillation occurs over a wide range of capillary numbers. At C = 2.834× 10-2,the oscillation ceases,and the fingertip and the two edges of the finger are located in the three expanding region,respectively (see Fig. 7(e)). As the capillary number increases (C = 1.526 × 10-1),the finger narrows,and then the two edges both reach the minimum depth and the oscillations reemerge (see Fig. 7(f)). The reoccurring oscillations occur over a narrow range of capillary numbers this time. As the capillary number increases further,the edges pass over the minimum depths,and an apparent shift from the wide finger to the narrow finger can be recognized (see Fig. 7(g)). Then,after the shift,the finger propagates wholly in one of the expanding regions of the cell for a higher capillary number (see Fig. 7(h)). All the finger patterns are obtained on the 600 × 51 × 10 grid except for Fig. 7(c),in which the oscillation is severe,and the pattern converges on the 660 × 56 × 12 grid.
Different from the asymmetric finger with the one-edge oscillation for n = 2 and the symmetric finger with the two-edge oscillation for n = 3,when n = 4,we obtain the asymmetric finger with the two-edge oscillation,and the evolution of the profile shape of finger with different capillary numbers is presented in Fig. 8. For a very low capillary number (C = 5.946 × 10-4), an almost straight interface is obtained (see Fig. 8(a)). As the capillary number increases (C = 2.773× 10-3),the oscillation occurs on one edge of the finger and is bounded by the two minimum depths (see Fig. 8(b)). As the capillary number increases (C = 5.715 × 10-3),an almost symmetric finger forms with the oscillation on the two edges of the finger,and the oscillation is constrained by the sidewalls (see Fig. 8(c)). As the capillary number increases further (1.169 × 10-2),the finger and the oscillation both lose their symmetry,one edge bulges of the finger and the other dents,and the wavelength of the oscillation reduces (see Fig. 8(d)). The strength of the oscillation is reduced with the increasing capillary number (C = 2.447× 10-2), as shown in Fig. 8(e). The oscillation always occurs in a wide range of capillary numbers. At C = 8.765 × 10-2,the oscillation ceases (see Fig. 8(f)). As the capillary number increases further to C = 1.477 × 10-1,the oscillation reoccurs,which may attribute to the decrease in

|
| Fig. 7 When n = 3 and A = 0.3,profile shapes of finger under different values of capillary number |

|
| Fig. 8 When A = 0.3 and n = 4,profile shapes of finger under different values of capillary number |
the transverse curvature when the interface extends backward from the fingertip (see Fig. 8(g)). The oscillation does not cease until the capillary number is high enough that the finger intends to shift from a wider one to a narrower one (see Fig. 8(i)). After that,the asymmetrical finger propagates at the highest capillary number (see Fig. 8(i)).
3.2 Finger widthThe above research shows that the introduction of the spatially periodic variation of depth brings a variety of finger patterns. For convenience of quantitative measurement,we define the relative width of the finger λ as the ratio of the area displaced by air to the total area, irrespective of the finger patterns. From the relation between the finger velocity U,the velocity at infinity V ,and the relative width,V = λU,it can be concluded that this definition is consistent with the classical one which is defined as the ratio of the finger width to the cell width.
For n = 1,the finger pattern at λ = 0.524 is given in the above section. Substitute λ = 0.524 into the Pitts’s solutions to obtain the finger shape in the conventional Hele-Shaw cell. Then, the shape profiles are superposed in Fig. 9. It shows that at λ = 0.524,the finger shape from the Pitts’s solutions is wider than the simulated finger in the modified Hele-Shaw cell. The reason for this is that the finger in the modified cell with n = 1 is thicker than that of the conventional cell. Therefore,with the same air occupation,the finger in the modified cell is narrower.

|
| Fig. 9 Comparison of superposed front part of computed finger shape (solid line) in modified Hele- Shaw cell with analytical solution (square) given by Pitts for conventional Hele-Shaw cell |
Then,the finger widths for n = 3,4 and A = 0.3,0.4 are examined at different capillary numbers,as shown in Fig. 10. In general,the finger width decreases with the increasing capillary number. When the capillary number is very low,as exemplified by the case shown in Fig. 7,the oil is displaced completely,and the relative finger width is approximately one. As the capillary number increases,the emergence of finger results in a sudden decrease in the finger width. After that,the finger width decreases slowly with the increasing capillary number and tends to be constant until the oscillations occur again. The reoccurring oscillations cause small increase in the finger width as the capillary number increases. After the reoccurring oscillations,the shift from the wide finger to the narrow finger results in a sudden decrease in the finger width and a sudden increase in the capillary number. This is because the shift of finger causes the shift of the propagating velocity of the fingertip,as shown in Fig. 11. Both the capillary number and the finger width are related to the velocity of fingertip,which is obtained from the gradient of the fitted lines in Fig. 11. The sudden increase of the gradient at 1.8 s results in a sudden change of the finger width and the capillary number. The shift occurs over a narrow range of capillary numbers. After the shift,there is another sudden decrease in the finger width and another sudden increase in the capillary number. Then,the finger width decreases slowly with the increasing capillary number. The finger width is slightly affected by the amplitude of depth perturbation. Before the reoccurring oscillations,the smaller amplitude of depth perturbation results in a little higher finger width. After that,there is no apparent difference for each other. The wavenumber of perturbation depth has little influence on the finger width.

|
| Fig. 10 Finger width R as function of capillary number C for A = 0.3 (triangle) and A = 0.4 (circle) of cell with b0 = 0.08 cm,W = 2.54 cm,and L = 30 cm when n = 3 (filled symbols) and n = 4 (open symbols) |

|
| Fig. 11 Location of fingertip versus time for C = 2.151 ×10 -1 for n = 3 and A = 0.3,together with linear fitting lines,where gradient of lines represents velocity of fingertip,and square and circle are locations before and after shift,respectively |
We study the viscous fingering instability in a modified Hele-Shaw cell by numerical simulation with the package OpenFOAM. One of the plates of the Hele-Shaw cell is changed to a wavy one so that the depth of the cell varies periodically. We mainly focus on the cell with spatially periodic variation of depth along the lateral direction. The results show that the wavenumber n of the depth perturbation and the capillary number C have great influence on the finger patterns. For n = 1,the finger pattern remains the same as that in a conventional cell,except for the narrower width. For n = 2,four different finger patterns are obtained at different capillary numbers,which are similar to those experimentally reported in the cell with the partial centered occlusion. When n increases further,new oscillatory finger patterns are captured,i.e., an asymmetric two-edge oscillatory one for n = 3 and an asymmetric two-edge oscillatory one for n = 4,respectively. Furthermore,we find for the first time that the oscillations occur over two ranges of C,and the oscillations disappear between the two ranges. The relation between the finger width and the capillary number has also been investigated for n = 3,4. As C increases, the finger width tends to a value far below 0.5,which is very different from the viscous fingering in a conventional Hele-Shaw cell. The wavenumber and the amplitude of the depth perturbation have relatively little effect on the finger width.
AcknowledgementsThe authors thank the OpenFOAM Foundation and OpenCFD Ltd. for the free and open source CFD software package—OpenFOAM.
| [1] | Saffman, P. G. and Taylor, G. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 245, 312-329(1958) |
| [2] | Engelberts, W. F. and Klinkenberg, L. J. Laboratory experiments on the displacement of oil by water from packs of granular material. The 3rd World Petroleum Congress, 28 May-6 June, The Hague, the Netherlands (1951) |
| [3] | Kessler, D. A., Koplik, J., and Levine, H. Pattern selection in fingered growth phenomena. Advances in Physics, 37(3), 255-339(1988) |
| [4] | Taylor, G. Cavitation of a viscous fluid in narrow passages. Journal of Fluid Mechanics, 16, 595-619(1963). |
| [5] | Ruschak, K. J. Coating flows. Annual Review of Fluid Mechanics, 17, 65-89(1985) |
| [6] | Reinelt, D. The primary and inverse instabilities of directional viscous fingering. Journal of Fluid Mechanics, 285, 303-327(1995) |
| [7] | Hull, D. Fractography:Observing, Measuring and Interpreting Fracture Surface Topography, Cambridge University Press, Cambridge (1999) |
| [8] | Clanet, C. and Searby, G. First experimental study of the Darrieus-Landau instability. Physical Review Letters, 80, 3867-3870(1998) |
| [9] | Ben-Jacob, E., Shmueli, H., Shochet, O., and Tenenbaum, A. Adaptive self-organization during growth of bacterial colonies. Physica A:Statistical Mechanics and Its Applications, 187, 378-424(1992) |
| [10] | Aldushin, A. and Matkowsky, B. Instabilities, fingering and the Saffman-Taylor problem in filtration combustion. Combustion Science and Technology, 133, 293-341(1998) |
| [11] | Ben Amar, M. Void electromigration as a moving free-boundary value problem. Physica D:Nonlinear Phenomena, 134, 275-286(1999) |
| [12] | Hele-Shaw, H. S. On the motion of a viscous fluid between two parallel plates. nature, 58, 34-36(1898) |
| [13] | Homsy, G. M. Viscous fingering in porous media. Annual Review of Fluid Mechanics, 19, 271-311(1987) |
| [14] | Ben-Jacob, E., Godbey, R., Goldenfeld, N., Levine, H., Mueller, T., and Sander, L. M. Experimental demonstration of the role of anisotropy in interfacial pattern formation. Physical Review Letters, 55, 1315-1318(1985) |
| [15] | Rabaud, M., Couder, Y., and Gerard, N. Dynamics and stability of anomalous Saffman-Taylor fingers. Physical Review A, 37, 935-947(1988) |
| [16] | McCloud, K. V. and Maher, J. V. Experimental perturbations to Saffman-Taylor flow. Physics Reports, 260, 139-185(1995) |
| [17] | Al-Housseiny, T. T., Tsai, P. A., and Stone, H. A. Control of interfacial instabilities using flow geometry. Nature Physics, 8, 747-750(2012) |
| [18] | De Lózar, A., Heap, A., Box, F., Hazel, A. L., and Juel, A. Tube geometry can force switchlike transitions in the behavior of propagating bubbles. Physics of Fluids (1994-present), 21, 101702(2009) |
| [19] | Pailha, M., Hazel, A. L., Glendinning, P. A., and Juel, A. Oscillatory bubbles induced by geometrical constraint. Physics of Fluids (1994-present), 24, 021702(2012) |
| [20] | Thompson, A. B., Juel, A., and Hazel, A. L. Multiple finger propagation modes in Hele-Shaw channels of variable depth. Journal of Fluid Mechanics, 746, 123-164(2014) |
| [21] | McLean, J. and Saffman, P. The effect of surface tension on the shape of fingers in a Hele Shaw cell. Journal of Fluid Mechanics, 102, 455-469(1981) |
| [22] | Tryggvason, G. and Aref, H. Numerical experiments on Hele Shaw flow with a sharp interface. Journal of Fluid Mechanics, 136, 1-30(1983) |
| [23] | DeGregoria, A. and Schwartz, L. A boundary-integral method for two-phase displacement in HeleShaw cells. Journal of Fluid Mechanics, 164, 383-400(1986) |
| [24] | Brackbill, J. U., Kothe, D. B., and Zemach, C. A continuum method for modeling surface tension. Journal of Computational Physics, 100, 335-354(1992) |
| [25] | Deshpande, S. S., Anumolu, L., and Trujillo, M. F. Evaluating the performance of the two-phase flow solver interFoam. Computational Science and Discovery, 5, 014016(2012) |
| [26] | Bensimon, D., Kadanoff, L. P., Liang, S., Shraiman, B. I., and Tang, C. Viscous flows in two dimensions. Review of Modern Physics, 58, 977-999(1986) |
| [27] | Pitts, E. Penetration of fluid into a Hele-Shaw cell:the Saffman-Taylor experiment. Journal of Fluid Mechanics, 97, 53-64(1980) |
| [28] | Tabeling, P. and Libchaber, A. Film draining and the Saffman-Taylor problem. Physical Review A, 33, 794-796(1986) |
 2016, Vol. 37
2016, Vol. 37


