Shanghai University
Article Information
- Xingzhe WANG, Longfei LI, Youhe ZHOU. 2016.
- Aeroelastic dynamics stability of rotating sandwich annular plate with viscoelastic core layer
- Appl. Math. Mech. -Engl. Ed., 37(1): 107-120
- http://dx.doi.org/10.1007/s10483-016-2012-9
Article History
- Received Jan. 9, 2015;
- in final form May 11, 2015
2. Department of Theoretical and Applied Mechanics, School of Mining and Safety Engineering, Shandong University of Science and Technology, Qingdao 266510, Shandong Province, China
As the basic elements, rotating structures such as beams, disks or plates, and shells are widely utilized in various machines such as floppy disks, VCDs/DVDs, hard disks, turbines, gyroscopes, and annular saw-blades. With the new generation of hard disk drives (HDDs) of high productivity and high capacity, and the high-speed annular saw-blades of precision machining being expected, the rotation speeds of the annular plates tend to be higher and higher so that the dynamic stability of them has become an important research topic[1].
The rotating disks may lose stability by buckling at a high speed, which is related to the natural frequency of backward traveling wave (BTW) of a rotating disk. Resonance will be excited under a stationary transverse load at a critical speed where the frequency of BTW is vanished. Lamb and Southwell[2] were the first to investigate the free vibration of a rotating disk. Since then, the free and forced vibrations, as well as the buckling stability related to the rotating thin-walled structures like shells, plates or disks, and beams, have attracted attention from many authors[3, 4, 5, 6, 7, 8, 9]. Lee and Waas[10] and Lee et al.[11] studied the vibration characteristics and dynamic instability of a rotating laminated annular plate by considering the effect of a frictional loading. Furthermore, many investigations on the three-layer sandwich structures with the viscoelastic core embedded between two elastic face layers have been performed[12, 13, 14, 15, 16]. Wang and Chen[17] studied the dynamic characters of a sandwich plate with two laminated face layers, in which the extensional and shear modules of viscoelastic central layer are described by complex constants. Chen and Chen[18] studied dynamic instability of the orthotropic sandwich circular plate subjected to a radial loading by Bolotin’s method. Based on Reddy’s refined highorder shear deformation theory, Meunier and Shenoi[19] analyzed the forced vibration of a fiber reinforced plastic sandwich plate under a transverse force. There are also a few works carried out on the subject of the dynamic characteristic of a rotating sandwich plate. Chen et al.[20] and Chen and Chen[21] studied dynamic instability and critical speeds of a rotating orthotropic sandwich circular plate undergoing a periodic radial loading by Bolotin’s method. In their investigations, the simple model with complex constants for extensional and shear modules of the viscoelastic core was used. The authors recently investigated the dynamic characteristics of frequencies and damping of the traveling waves for the rotating laminated plate with the viscoelastic core. In the above works, the extensional and shear modules of the viscoelastic central layer were described by complex constants, which was not reasonable for a rotating structure. Because the behavior of viscoelastic material strongly depends on the frequency as the rotating speed increases, in our research, we introduce the frequency-dependent complex modulus for the viscoelastic layer[22].
There is another kind of aeroelastic instability, besides the buckling instability, which is called disk flutter for a disk rotating in air at a higher speed beyond the critical one. The rotating disk may be unstable aerodynamically arising from the coupling with surrounding airflow to induce the disk vibration with the larger amplitude. Some empirical models which are related to the air pressure loadings acting on the disk vibration and the flutter have been proposed. Hosaka and Crandall[23] and Hansen[24] predicted flutter characters in enclosed and unenclosed disks by a rotating damping model. The acoustic coupling in disk stacks was modeled by some discrete springs[25, 26]. These models may explain certain instability and vibration coupling characters in the rotating disks, but some coefficients in these models have to be determined by experiment. Kim et al.[27] and Hansen et al.[28] suggested an experimental method to predict the disk flutter based on the generalized rotating damping model in which the damping force varying with the speed of the disk was estimated experimentally. In these aeroelastic models, the parameters are dependent on the disk rotation speed, the viscosity of the fluid, the mode frequencies, and the disk-enclosure configuration, which may limit the use of the model. Wang and Huang[29] further simplified the above aeroelastic model by some nondimensional constants instead of the coefficient operators according to the experimental data. The results showed that the predicted values of the mode frequencies, critical speeds, and flutter speeds agree well with the experimental ones. Based on the rotating damping model, Wang and Huang[30] proposed the acoustic feedback control method to decrease the flutter speeds of a rotating disk in an enclosure and studied the effect of the sizes and placements of the distributed piezoelectric actuators on the performance of feedback control. In the present work, the sandwich plate with a viscoelastic core layer is introduced to increase the aeroelastic stability due to the high energy dissipation performance of viscoelastic materials.
In this paper, we suggest a traveling wave dynamic model for a rotating sandwich annular plate with a viscoelastic core layer taking into account the surrounding airflow. The all governing and boundary condition equations of the aeroelastic system are obtained based on Hamilton’s principle. In the modeling, the viscoelastic behavior is simulated by the frequencydependent complex modulus model[31], and the aerodynamic loading exerted to the rotating annular plate is described by the simplified rotating damping model[29, 30]. Galerkin’s methodis used to obtain the solutions of fundamental equations for the dynamics and stability of the rotating sandwich plate. The frequencies and damping of forward and backward traveling waves of the rotating plate, which are dependent upon the geometrical and material parameters of the plate, are obtained numerically. The critical speed and the flutter speed varying with the geometrical and material parameters of the sandwich plate are discussed.
2 Fundamental equationsA three-layer symmetrical sandwich annular plate is sketched in Fig. 1 with the inner and outer radii ri and ro, respectively, rotating in air with a constant rotation speed Ω. The sandwich plate is composed of the constraining layer and the host plate layer, which are assumed to be homogeneous, isotropically elastic, and viscoelastic layers. A space-fixed coordinate system (r, θ, z) is introduced in the modeling. The rotating annular plate with small transverse motion is modeled with the linear Kirchhoff’s plate theory. The displacements of the constraining and host plate layers can be expressed by[32]
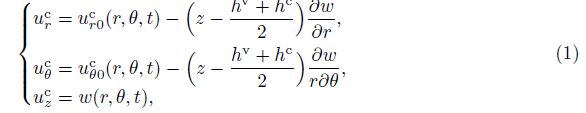
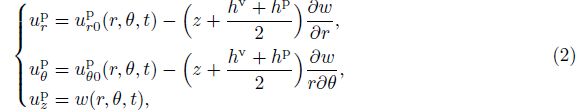
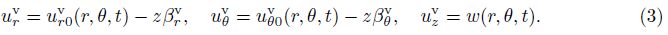

|
| Fig. 1 Sketch of rotating sandwich annular plate with viscoelastic core layer |
To comply with no-slip constrains between layers[32], one can get the displacements of the viscoelastic layer by applying the displacement continuity condition at the interface of layers to Eqs. (1)-(3),
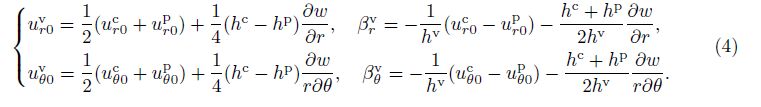
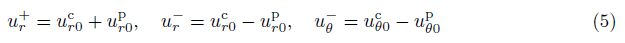
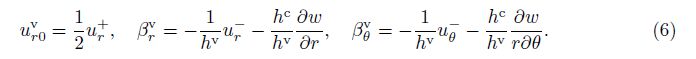
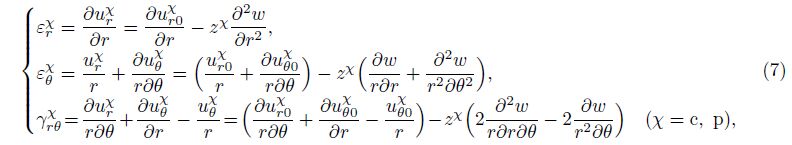
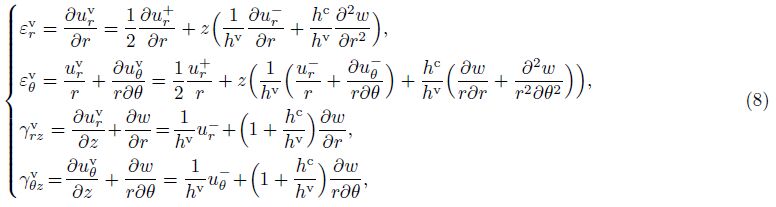
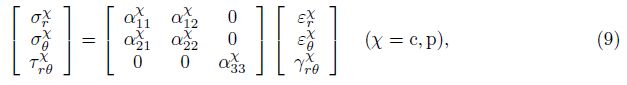
For the middle viscoelastic layer, the frequency-dependent constitutive relationship with complex modulus is adopted[15],
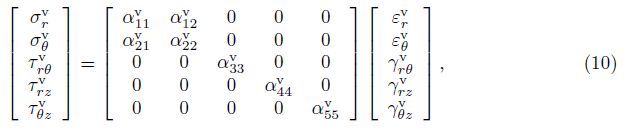
For the rotating sandwich annular plate, the variation of the kinetic energy of K gives
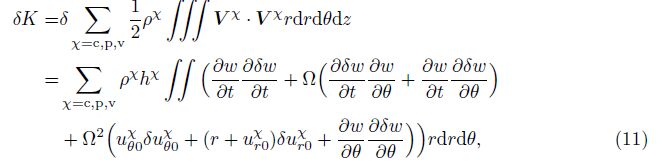
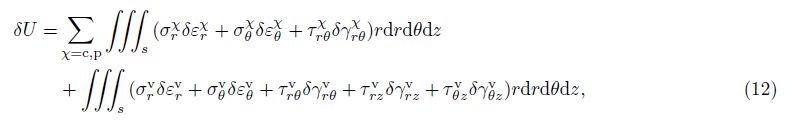
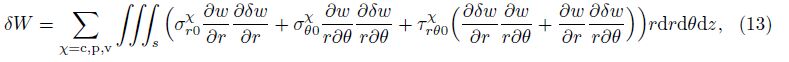
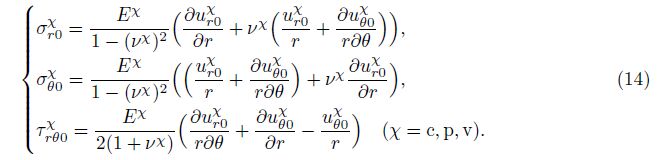
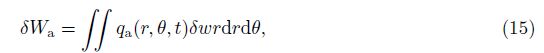
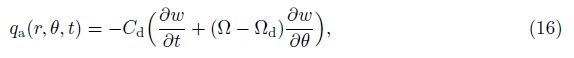
For convenience of analysis, the following nondimensional variables are introduced:
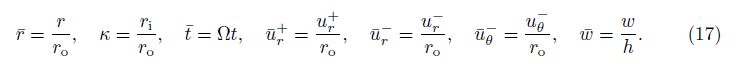
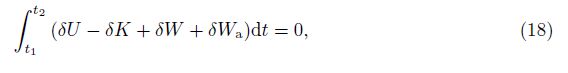
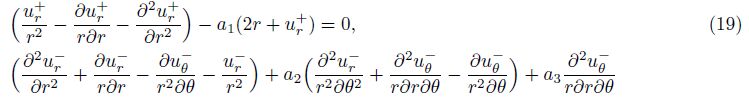
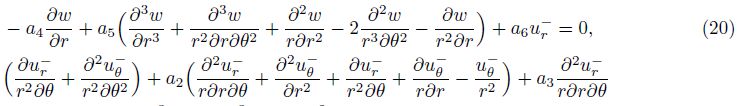
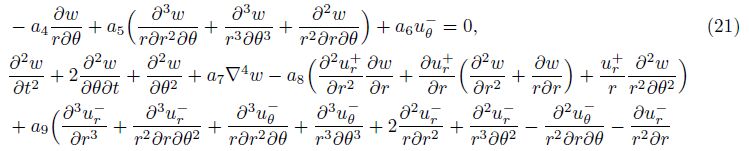
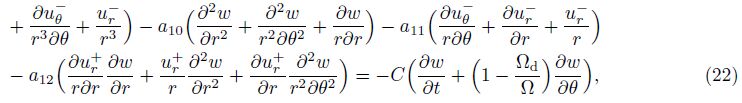
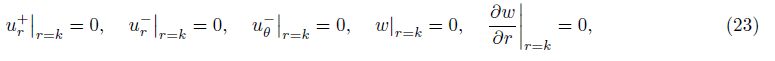
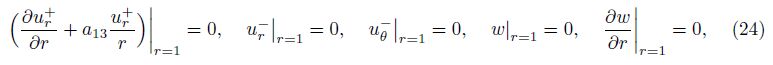
To solve the dynamic equations, we use an approximation method and assume that the displacements are in the forms of
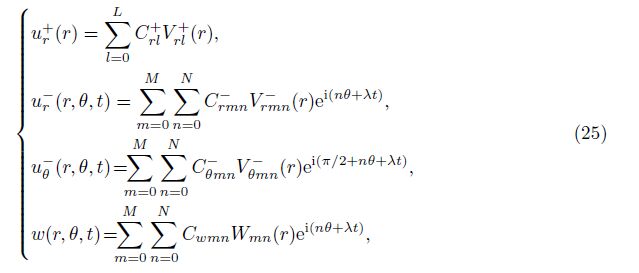
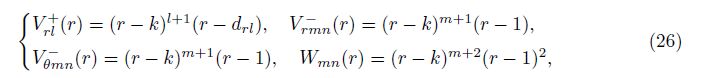
With Galerkin’s method, we substitute the first equation of Eq. (25) into the nondimensional Eq. (19) and calculate the inner product withVr$\hat{l}$+(r) ($\hat{l}$ = 0, 1, · · · , L)to get ACL = D, in which CL = [Cr0+, Cr1+, · · · , CrL+]T.A and D are, respectively, an (L+1)×(L+1) matrix and an (L+1) column matrix whose entries are the same as those in Ref. [22]. Upon substituting the last three equations of Eq. (25) into Eqs. (20)-(22) and calculating the inner products withVr $hat{m}$n−(r)e−i(nθ+λt), Vθ $hat{m}$n−(r)e−i(π2+nθ+λt), andW$hat{m}$n(r)e−i(nθ+λt)( $hat{m}$ = 0, 1, · · · , M), respectively, as well as eliminating the coefficients Crmn− and Cθmn, − one can get a matrix equation forthe coefficients Cwmn as
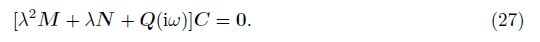
The characteristic equation for the condition of nontrivial solutions for Eq. (27) is
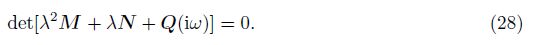
Case studies are conducted to show the dynamic characteristics of a sandwich annular plate rotating in air. First, we take all layers of the plate the same material so that it can be compared with the results of a monolayer plate for verification. The natural frequencies of the stationary plate (i.e., Ω = 0 r·min-1) and rotating plate (i.e., Ω = 1 000 r·min-1) with and without surrounding airflow are obtained to compare with the results in Refs. [30] and [31]. There shows good agreement between them even as the truncation number takes small ones like L = 5 and M = 5. Then, we study the dynamic character of a sandwich annular plate with the viscoelastic core layer. Young’s modulus, Poisson’s ratio, and the density of the constraining layer and the host layer are Ec = 200 GPa, νc = 0.3, and ρc = 7 840 kg·m−3, respectively.The density and Poisson’s ratio of the viscoelastic core layer are chosen as ρv = 500 kg·m−3 and νv =0.3, respectively. The frequency-dependent complex Young’s modulus and shearing modulus of the viscoelastic core are used by[31]
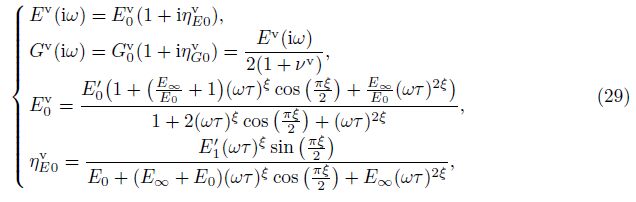
The frequencies for all FTW modes increase with the rotation speed of the sandwich annular plate. The frequencies of BTWs decrease at first and vanish at a critical speed where the buckling occurs, finally increase beyond that speed, as shown in Fig. 2(a). In the simulation, the thickness ratio δ = hv/h = 0.6. A stationary transverse force may excite resonance of the plate at critical speeds. The dampings for some higher BTW modes, as shown in Fig. 2(b), are initially positive and increase and then decrease to reach a negative value as the rotation speed increases. The negative value of the damping for BTW modes, Im(λ)<0, means that the plate loses stability aeroelastically, and flutter occurs. The speed at which Im(λ) equals zero is defined as the flutter speed. The plate is stable at modes (m = 0 and n = 0, 1, 2) due to the positive values of the frequencies and damping at these modes. Furthermore, Fig. 3 shows that the critical speed and the flutter speed depend on the vibration modes. We can see that the critical and flutter speeds decrease with the nodal diameter n and increase thereafter. They reach the minimum values of the critical speed for the mode (0, 22) and the flutter speed for the mode (0, 14), respectively. The modes, at which buckling and flutter take place and the corresponding speeds are the minimums, are named as the critical and flutter modes of the rotating plate, respectively. The critical mode and the flutter mode are also found to vary with the geometrical and material parameters of the sandwich annular plate.

|
| Fig. 2 Mode frequencies and damping of BTWs varying with rotating speed (δ = 0.6) |

|
| Fig. 3 Critical and flutter speeds varying with vibration modes |
There shows obvious influence of the thickness and material parameters on the frequencies and damping and the stability character of the rotating sandwich plate. The mode frequency and the critical speed varying with the thickness ratio δ are shown in Fig. 4. The mode frequencies increase with the thickness of the viscoelastic core layer, reach the maximum values at δ = 0.85, and then decrease lightly, as shown in Fig. 4(a). The results of the critical speeds are plotted in Fig. 4(b), in which the minimum values for different modes are obtained at about δ = 0.5. By comparisons on all the modes, we can see that for different thickness ratios δ, it shows different critical modes. For example, at the ranges of 0.1 < δ < 0.4 and 0.82 < δ < 0.9, the mode (0, 10) is the critical mode, and at 0.4 < δ < 0.6 and 0.6 < δ < 0.82, the critical modes are (0, 20) and (0, 30), respectively. The minimum rotation speeds of buckling and flutter instability for the sandwich plate are plotted in Fig. 4(c). One can see that, for the buckling instability, the critical speed reaches the minimum value at δ = 0.45 and the maximum value at δ = 0.9. As for the flutter instability, the minimum flutter speed reaches at δ = 0.3, and the maximum value reaches at δ = 0.88. With the increase of δ, the critical and flutter speeds are improved obviously. The flutter mode and the flutter frequency where flutter occurs varying with the thickness ratio are listed in Table 1. It can be seen that, different thickness ratios δ for the sandwich plate are always associated with different flutter modes and flutter frequencies, and the frequency gets the maximum value at about δ = 0.6. Figures 5(a) and 5(b) show the mode frequencies and damping of the rotating sandwich plate for different Young’s modulus ratios. In the simulation, we choose δ = 0.6 and Ec = 200 GPa. From the figure, the frequencies of the FTW and BTW modes increase with the ratio of Young’s modulus RE =E' 0/Ec, while the mode damping decreases. The critical and flutter speeds depending on the Young’s modulus ratio are shown in Fig. 5(c). It shows that the critical and flutter speeds increase with the ratio. These may be explained by the enhanced bending stiffness. Furthermore, the flutter mode and the flutter frequency for different ratios of Young’s modulus are listed in Table 2. The effect of the loss factor coefficient is obtained in Fig. 6. Figures 6(a) and6(b) indicate that the mode frequencies and damping increase with the loss factor coefficientE'1. Figures 6(c) and6(d) plot the critical speed and the flutter speed varying with the loss factor coefficient E'1, respectively. It is shown that the critical and flutter speeds are improved as the loss factor coefficient increases due to the increase of damping of the rotating plate system, which improves the dynamic stability of the plate. More details on the flutter modes and flutter frequencies with the loss factor coefficient are listed in Table 3.

|
| Fig. 4 Effect of thickness ratio δ on dynamic behaviors of rotating sandwich annular plate (Ω = 2 000 r·min−1) |

|
| Fig. 5 Effect of Young’s modulus ratio on dynamic behaviors of rotating sandwich annular plate (δ = 0.6 and Ω = 2 000 r·min−1) |

|
| Fig. 6 Effect of loss factor coefficient on dynamic behaviors of rotating sandwich annular plate (δ = 0.6 and Ω = 2 000 r·min−1) |
The dynamic and stabilization characteristics of a rotating sandwich plate with a frequencydependent viscoelastic core are analyzed quantificationally. The effect of the thickness and material parameters on frequencies and damping of FTWs and BTWs of the rotating plate and the dynamic stability are discussed. The numerical results show that the dynamic stability can be enhanced due to the increased critical and flutter speeds at some particular values of the thickness ratio as well as Young’s modulus ratio and the loss factor coefficient.
Appendix AThe entries for matrices M, N, and Q are

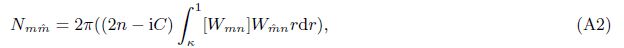
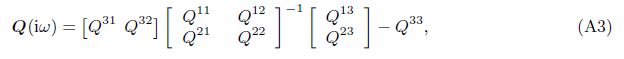
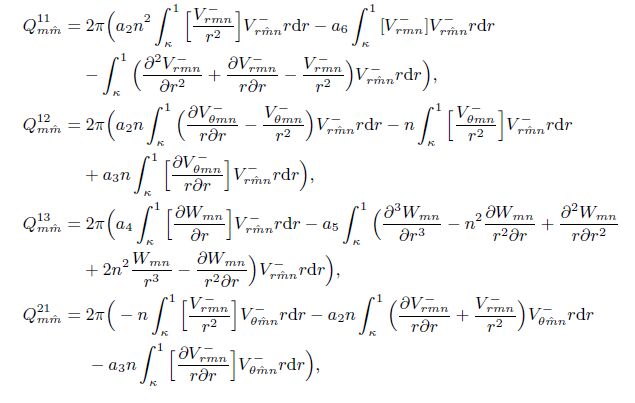
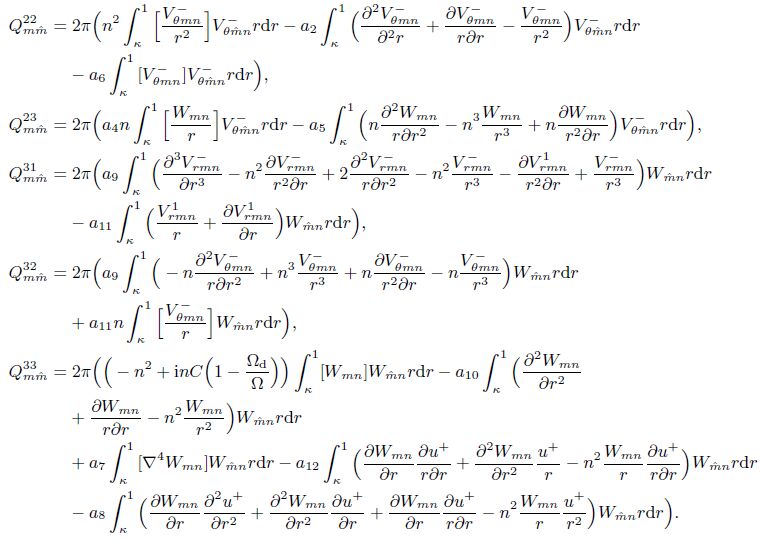
| [1] | Shen, I. Y. Vibration of flexible rotating disks. The Shock and Vibration Digest, 32, 267–272(2000) |
| [2] | Lamb, H. and Southwell, R. V. The vibration of a spinning disk. Proceedings of the Royal Society,99, 272–280 (1921) |
| [3] | Eversman, W. and Dodson, R. O. Free vibration of a centrally clamped spinning circular disk.American Institute of Aeronautics and Astronautics Journal, 7, 2010–2012 (1969) |
| [4] | Bauer, H. Vibration of a rotating uniform beam. Journal of Sound and Vibration, 72, 177–189(1980) |
| [5] | Chen, J. S. Stability analysis of a spinning elastic disk under a stationary concentrated edge load.Journal of Applied Mechanics, 61, 788–792 (1994) |
| [6] | Shiau, T. N., Yu, Y. D., and Kuo, C. O. Vibration and optimum design of rotating laminated blades. Composites Part B: Engineering, 27, 173–183 (1996) |
| [7] | Lam, K. Y., and Li, H. On free vibration of a rotating truncated circular orthotropic conical shell. Composites Part B: Engineering, 30, 135–144 (1999) |
| [8] | Li, H. Influence of boundary conditions on the free vibration of rotating truncated circular multilayered conical shells. Composites Part B: Engineering, 31, 265–275 (2000) |
| [9] | Liew, K. M., Hu, Y. G., Ng, T. Y., and Zhao, X. Dynamic stability of rotating cylindrical shells subjected to periodic axial loads. International Journal of Solids and Structures, 43, 7553–7570(2006) |
| [10] | Lee, D. andWaas, A. M. Stability analysis of a rotating multi-layer annular plate with a stationary frictional follower load. International Journal of Mechanical Sciences, 39, 1117–1138 (1997) |
| [11] | Lee, D., Waas, A. M., and Karnopp, B. H. Analysis of a rotating multi-layer annular plate modeled via layerwise zig-zag theory: free vibration and transient analysis. Computer and Structures, 63,313–335 (1998) |
| [12] | Mead, D. J. and Markus, S. The forced vibrations of a three-layer damped sandwich beam with arbitrary boundary conditions. Institute of Aeronautics and Astronautics Journal, 10, 163–175(1969) |
| [13] | Douglas, B. E. and Yang, J. C. S. Transverse compressional damping in the vibratory response of elastic-viscoelastic-elastic beams. Institute of Aeronautics and Astronautics Journal, 16, 925–930 (1978) |
| [14] | Rao, M. D., Echempati, R., and Nadella, S. Dynamic analysis and damping of composite structures embedded with viscoelastic layers. Composites Part B: Engineering, 28, 547–554 (1997) |
| [15] | Meunier, M. and Shenoi, R. A. Dynamic analysis of composite sandwich plates with damping modeled using high-order shear deformation theory. Composite Structure, 54, 243–254 (2001) |
| [16] | Nayak, A. K., Moy, S. S. J., and Shenoi, R. A. Free vibration analysis of composite sandwich plates based on Reddy’s higher-order theory. Composites Part B: Engineering, 33, 505–519 (2002) |
| [17] | Wang, H. J. and Chen, L. W. Vibration and damping analysis of a three-layered composite annular plate with a viscoelastic mid-layer. Composite Structures, 58, 563–570 (2002) |
| [18] | Chen, Y. R. and Chen, L. W. Axisymmetric parametric resonance of polar orthotropic sandwich annular plates. Composite Structures, 65, 269–277 (2004) |
| [19] | Meunier, M. and Shenoi, R. A. Forced response of FRP sandwich panels with viscoelastic materials. Chen,Y. R., Chen, L. W., and Wang, C. C. Axisymmetric dynamic instability of rotating polar orthotropic sandwich annular plates with a constrained damping layer. Composite Structures, 73, 290–302 (2006) |
| [20] | Chen, Y. R., Chen, L. W., and Wang, C. C. Axisymmetric dynamic instability of rotating polar orthotropic sandwich annular plates with a constrained damping layer. Composite Structures, 73, 290–302 (2006) |
| [21] | Chen, Y. R. and Chen, L. W. Vibration and stability of rotating polar orthotropic sandwich annular plates with a viscoelastic core layer. Composite Structures, 78, 45–57 (2007) |
| [22] | Li, L. F., Wang, X. Z., and Zhou, Y. H. Dynamic characteristics of traveling waves for a rotating laminated circular plate with viscoelastic core layer. Journal of Sound and Vibration, 330, 2836–2847 (2011) |
| [23] | Hosaka, H. and Crandall, S. Self-excited vibrations of a flexible disk rotating on an air film above a flat surface. Acta Mechanica, 3, 115–127 (1992) |
| [24] | Hansen, M. Aeroelasticity and Dynamics of Spinning Disks, Ph. D. dissertation, Technical University of Denmark (1999) |
| [25] | Orgun, C. O. and Tongue, B. H. On localization in coupled, spinning, circular plates. ASME Journal of Vibration and Acoustics, 116, 555–561 (1994) |
| [26] | Park, J. S. and Shen, I. Y. Aerodynamically and structurally coupled vibration of multiple corotating disks. ASME Journal of Vibration and Acoustics, 126, 220–228 (2004) |
| [27] | Kim, B. C., Raman, A., and Mote, C. D., Jr. Prediction of aeroelastic flutter in a hard disk drive. Journal of Sound and Vibration, 238, 309–325 (2000) |
| [28] | Hansen, M. H., Raman, A., and Mote, C. D., Jr. Estimation of nonconservative aerodynamic pressure leading to flutter of spinning disks. Journal of Fluids and Structures, 15, 39–57 (2001) |
| [29] | Wang, X. Z. and Huang, X. Y. A simple modeling and experiment on dynamic stability of a disk rotating in air. International Journal of Structural Stability and Dynamics, 8, 41–60 (2008) |
| [30] | Wang, X. Z. and Huang, X. Y. Feedback control and optimization for rotating disk flutter suppression with actuator patches. Institute of Aeronautics and Astronautics Journal, 44, 892–900(2006) |
| [31] | Galucio, A. C., Deu, J. F., and Ohayon, R. Finite element formulation of viscoelastic sandwich beams using fractional derivative operators. Computational Mechanics, 33, 282–291 (2004) |
| [32] | Yu, S. C. and Huang, S. C. Vibration of a three-layered viscoelastic sandwich circular plate. International Journal of Mechanical Sciences, 43, 2215–2236 (2001) |
 2016, Vol. 37
2016, Vol. 37





