Shanghai University
Article Information
- Boyang DING, A. H. D. CHENG, Zhanglong CHEN. 2016.
- Decoupling coefficients of dilatational wave for Biot's dynamic equation and its Green's functions in frequency domain
- Appl. Math. Mech. -Engl. Ed., 37(1): 121-136
- http://dx.doi.org/10.1007/s10483-016-2015-9
Article History
- Received Mar. 16, 2015;
- in final form Jun. 6, 2015
2. Department of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China;
3. College of Civil Engineering and Architecture, University of Mississippi, Mississippi 38677-1848, U. S. A
Saturated soil can be modeled as a two-phase medium (a poroelastic medium). Researchers and engineers have used the poroelastodynamics theory to study seismicity,earthquake engineering,geophysics,and acoustics for several decades. The development of the theory and its applications can be found in the standard literature[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].
The poroelastodynamics theory was pioneered by Biot[1, 2]. The theory assumes a linear elastic porous solid undergoing small deformation with a fluid flow governed by Darcy’s law. Biot predicted the propagation of two dilatational waves and one distortional wave in this two-phase porous medium. The prediction has been observed in the laboratory by Plona[11],Ding[12],and Plona and Johnson[13].
Most of the studies of poroelastodynamics were done in the frequency domain,because the results are easier to be obtained,and the time domain solution can be constructed using the Fourier transform. Previous works include Refs. [14]-[23].
The benefits of the computational methods applied to poroelastodynamics have been reviewed by Schanz[24]. The boundary element method (BEM) has the advantage of reducing the number of dimensions in the computation,and using Green’s functions as the weighing function of the integral equations produces more accurate results. The superposition of Green’s functions also satisfies the radiation condition at the far field. Hence,the BEM provides a useful and effective tool for computational soil dynamics. For a specified group of problems,the BEM is also amenable for treatment of computational technology such as the object-oriented programming[25].
Cheng et al.[4] presented Green’s functions of poroelastodynamics utilizing an analogy between the dynamic thermoelasticity and the dynamic poroelasticity in the frequency domain. The solution was presented as the u-p formulation,as the corresponding quantity to the temperature was the pore pressure. In this work,we present a new methodology for deriving Green’s functions,which has the advantage of decoupling the fast and slow dilatational waves. The methodology is the same as that presented by Ding et al.[26]. However,a special term “decoupling coefficient” (for the fast and slow dilatational waves) is proposed and expressed in this paper. Based on the formulation,we then carry out the numerical implementation and plot these curves based on a set of parameters. The correctness of the solution is demonstrated by numerically comparing the current solution with Cheng’s previous solution. The separation of the two dilatational waves in the present methodology allows them to be more accurately evaluated than they are combined. This accuracy is particularly useful for the slow wave,whose magnitude decay is much quicker than that of the fast wave. This can be advantageous for numerical implementation in methods like the BEM and in other applications.
2 Governing equations and Green’s functions of dynamic poroelasticityBiot’s governing equations for the dynamic poroelasticity are as follows[1, 2]:
The constitutive equations are
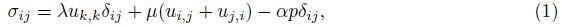

The equilibrium equation is

The generalized Darcy’s law of the fluid phase is
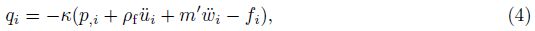

The continuity equation of the fluid phase is

In the above,λ and μ are Lam$\overset{'}{\mathop{e}}\,$ constants,α is Biot’s effective stress coefficient,and M is Biot’s modulus,which is the inverse of a storage coefficient,u and w are the displacement of the solid phase and the average displacement vector of the fluid phase relative to the solid phase,respectively ($\ddot u$ = d2u/dt2,$\ddot w$ = d2w/dt2),ρ and ρf are the total mass density (combined solid and fluid phases) and the fluid mass density,respectively (ρ = (1−β0)ρs+β0ρf,where ρs is the mass density of the solid phase). ρa is the apparent mass density. β0 is the porosity. λc,μ,α,and M are four independent poroelastic constants. We also note that eij = (ui,j + uj,i)/2 is the strain tensor of the solid phase,and e = eii is the volumetric strain of the solid phase. The relative volumetric strain of the fluid phase is wi,i. ui and wi are components of u and w in the ith direction,respectively. If a medium is always in a saturated situation in the dynamic process,we have $\dot w$ i,i = qi,i in Eq. (6). ζ = −wi,i is the variation in the fluid content,and χ is a fluid source. Other terms include: σij ,the total stress; p,i,the gradient of the pore pressure in the ith direction; Fi and fi,the body forces of the solid and fluid phases in the ith direction,respectively; κ = k/η,where k is the permeability,and η is the dynamic viscosity of the fluid; and δij ,the Kronecker delta with i,j = 1,2,3. For Biot’s parameters α and M,we find the following relations:
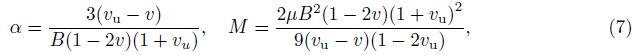
The above equations can be combined to give the following two coupled equations for the dynamic poroelasticity[4]:
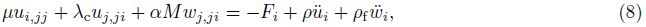
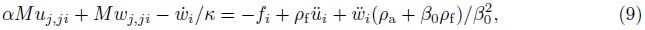
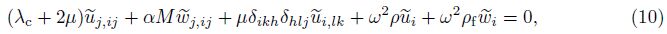
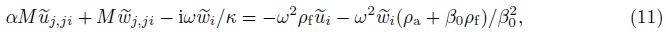
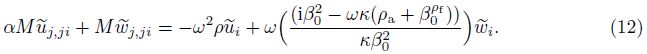
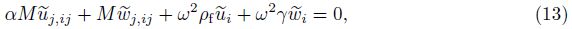
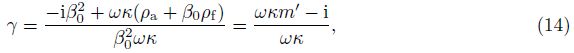
(i) Components of non-divergence field
If $\tilde{u}$ and $\tilde{w}$ in Eq. (11) are the components of the non-divergence field,we can derive the following:


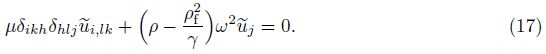


(ii) Components of irrotational field
If $\tilde{u}$ and $\tilde{w}$ are the components of the irrotational field,we can suppose



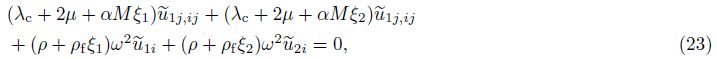
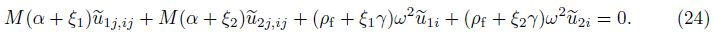
Equations (23) and (24) can be put into the forms that are more suitable for describing the wave equations as follows:
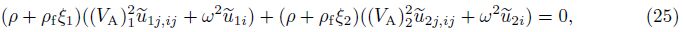
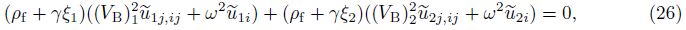
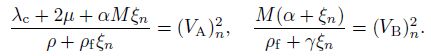
As analyzed by Biot[1],there exist only two irrotational waves,i.e.,one fast dilatational wave and one slow dilatational wave. Therefore,we have
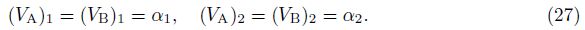
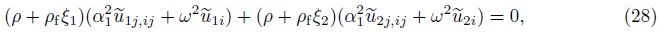
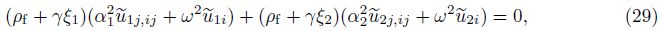
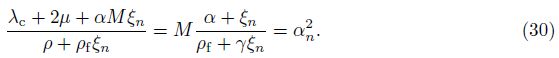
If a concentrated force${{\tilde{F}}_{j}}$ = F0δ(x − ς)ej (where F0 is the magnitude of force,ej is a unit vector in the jth direction,and δ is the Dirac delta function) is assumed to act at a point ς in a poroelastic medium,Eq. (28) can be written as
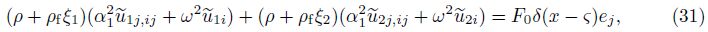
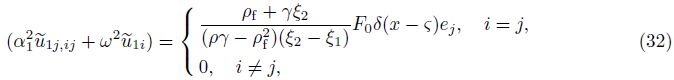
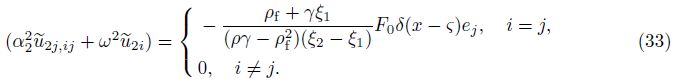
Hence,we have the following familiar classical solutions:
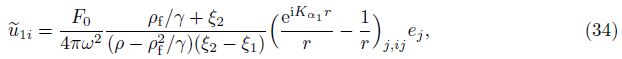
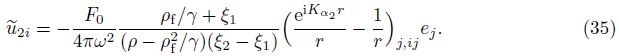
In Eqs. (34) and (35),Kαn = ω/αn are the wave numbers of the fast or slow dilatational wave,and r = |r| = |x − ς| is the distance between the source point and the field point.
Similarly,we can obtain the solution of the distortional wave from Eq. (18)[23],
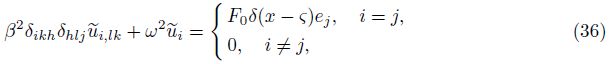
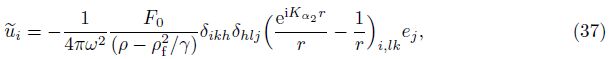
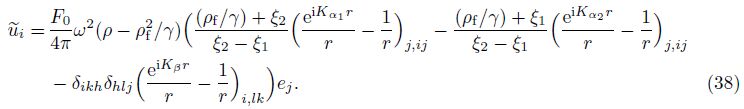
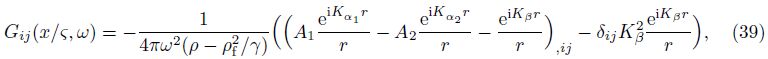
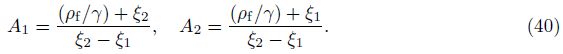
We can define A1 and A2 in Eq. (40) as “decoupling coefficients” for decomposition of the fast and slow dilatational waves of Eq. (12). Equation (40) is also the expression of “decoupling coefficients”. The form of Gij(x/ς,ω) was written as $\tilde{u}_{ij}^{f}$ by Cheng et al.[4]. Based on a deduction procedure shown in Appendix A,Eq. (40) can be recast as
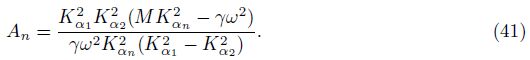
G4i(x/ς,ω) (as $\tilde{p}_{j}^{f}$ in Cheng et al.[4]) is defined as the pore pressure at the field point x due to a unit concentrated force acting at the source point ς in the ith direction. From Eqs. (11) and (3),we have[25]
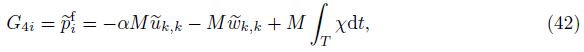

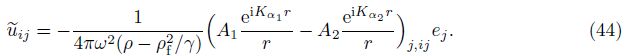
Employing Eq. (21),we obtain the component of the irrotational field $\tilde{w}$ subjected to a unit force as follows:
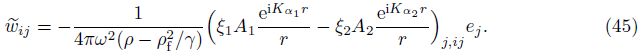
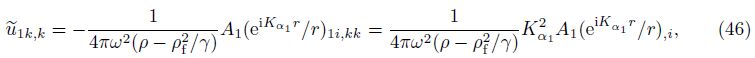
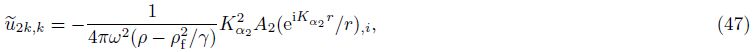
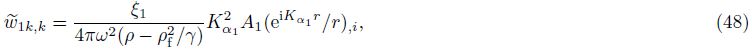
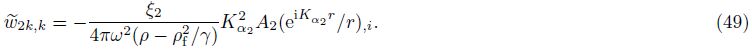
Substituting Eqs. (46)-(49) into Eq. (43),we are ready to write a concise result,
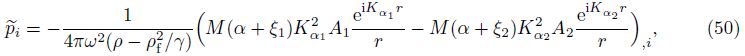
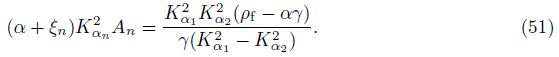
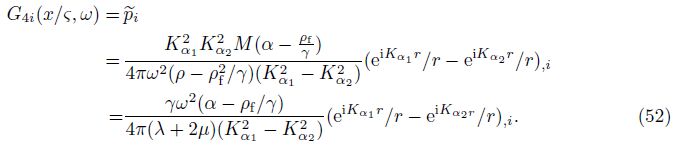
Gi4(x/ς,ω) is defined as the displacement at the field point x in the ith direction due to the injection of a unit volume of fluid into the pore at the field point ς. There is a simple expression derived from Betti’s theorem of reciprocity as follows:
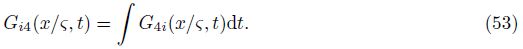

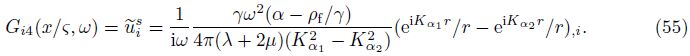
Similar to Gi4(x/ς,ω),G44(x/ς,ω) is defined as the pore-fluid pressure at the field point x due to the injection of a unit volume fluid at the source point ς. Employing the definition of Gi4 and Eq. (43),we can obtain
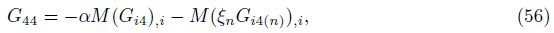
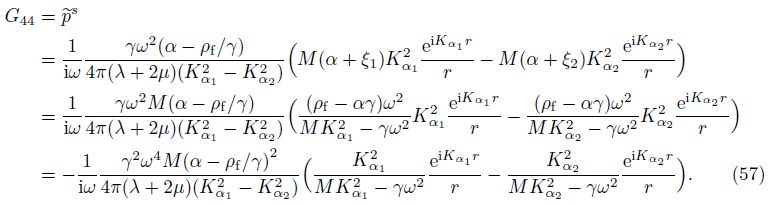
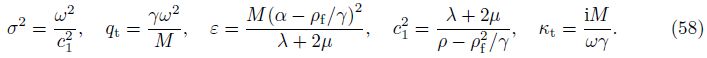
As the approaches and the various notations are different in the current paper and Ref. [4],it is important to compare the numerical results of the two solutions. For convenience,the dimensionless displacement,the pore pressure,and the relevant physical parameters are defined as follows[27, 28]:
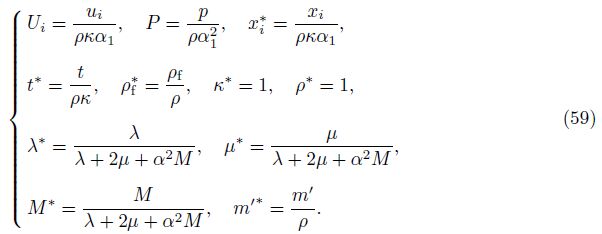
The original dimensional parameters and the corresponding values are shown in Table 2. The dimensionless homologous parameters substituted into formulas for computation are λ* = 0.171 5,μ* = 0.300 7,M* = 0.374 2,α = 0.779,κ* = 1,ρ* = 1,and ρf* = 0.432 5[27, 28]. For the source point ς* = (0,0,0) and the field point x* = (0.1,0.15,0.2) ,the results of numerical implementation are shown in Figs. 1-6. The dashed lines are the results in Ref. [4]. Good agreement between the corresponding curves can be easily assessed.

|
| Fig. 1 G11 versus frequency at ς∗= (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 2 |

|
| Fig. 2 G22 versus frequency at ς∗= (0, 0, 0) and x∗= (0.1, 0.15, 0.2) for case in Table 2 |

|
| Fig. 3 G33 versus frequency at ς∗ = (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 2 |

|
| Fig. 4 G41 versus frequency at ς∗ = (0, 0, 0) and x∗= (0.1, 0.15, 0.2) for case in Table 2 |

|
| Fig. 5 G14 versus frequency at ς∗= (0, 0, 0)and x∗ = (0.1, 0.15, 0.2) for case in Table 2 |

|
| Fig. 6 G44 versus frequency at ς∗= (0, 0, 0) and x∗ = (0.1, 0.15, 0.2) for case in Table 2 |
In order to further confirm the stability of the numerical implementation,we change the dimensionless parameters to λ* = 0.128 6,μ* = 0.274 6,M* = 0.467 9,α = 0.83,and ${{m}^{'*}}$ = 2.256. The dimensionless parameters ρ*,ρf* ,κ*,and the coordinates of the source point and the field point are maintained. The computational results are shown in Figs. 7-12. The dashed lines are results obtained by Cheng et al.[4]. Similarly,good agreement between the corresponding curves can be easily assessed.

|
| Fig. 7 G11 versus frequency at ς∗= (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 3 |

|
| Fig. 8 G22 versus frequency at ς∗= (0, 0, 0) and x∗= (0.1, 0.15, 0.2) for case in Table 3 |

|
| Fig. 9 G33 versus frequency at ς∗ = (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 3 |

|
| Fig. 10 G41 versus frequency at ς∗ = (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 3 |

|
| Fig. 11 G14 versus frequency at ς∗ =(0, 0, 0) and x∗= (0.1, 0.15, 0.2) for case in Table 3 |

|
| Fig. 12 G44 versus frequency at ς∗ = (0, 0, 0)and x∗= (0.1, 0.15, 0.2) for case in Table 3 |
(i) The above presented results are three-dimensional. The two-dimensional (plan strain) Green’s functions can also be useful in many applications. De Hoop[29] proposed that the two-dimensional Green’s function can be obtained by integrating of the three-dimensional Green’s function over the x3-axis (z-axis). Manolis[30] proved that De Hoop’s method was feasible and accurate. Ding et al.[31] integrated the three-dimensional Green’s functions with respect to the x3-axis in (−∞,+∞) to obtain the two-dimensional Green’s functions of solid phase. In fact,for the two-dimensional Green’s functions,we should pay attention to the following identity:
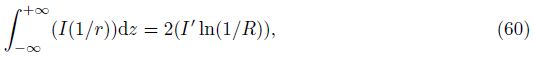
(ii) Equations (38) and (39) are the solutions of Philippacopoulos’s paper[21] also,but these are not Green’s functions of the fluid source as claimed by Philippacopoulos. The solutions in Ref. [4] are the complete results for the u-p formulation of solutions of Biot’s dynamic equation.
6 ConclusionsBased on Green’s functions of the displacement field for the solid and fluid phases of poroelastodynamics presented in this paper,we can make the following conclusions:
(i) The solutions of Green’s functions with the concentrated force which is provided by Cheng et al.[4] are valid and concise. They can be effectively used in the frequency domain for the numerical implementation of dynamic poroelastic problems.
(ii) Analogy between the dynamic thermoelasticity and the dynamic poroelasticity in the frequency domain may be an important approach to solve complex problems pertaining to the corresponding poroelastic governing differential equations.
(iii) The expressions associated with the decoupling of the fast and slow dilatational waves in this paper (Eq. (40)) (decoupling coefficients) will be beneficial in the research of poroelastodynamics.
Appendix AEmploying Eqs. (25) and (26),we have
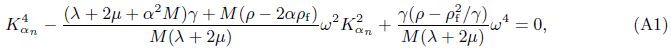

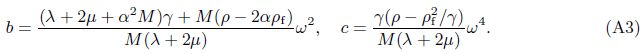
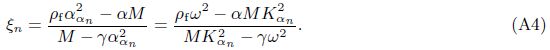
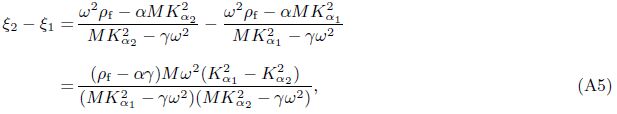
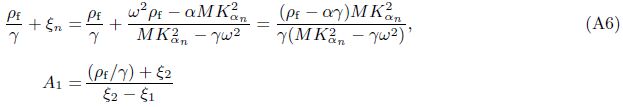
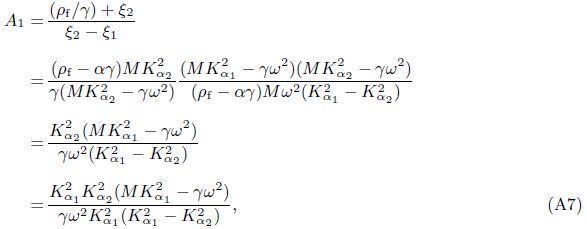
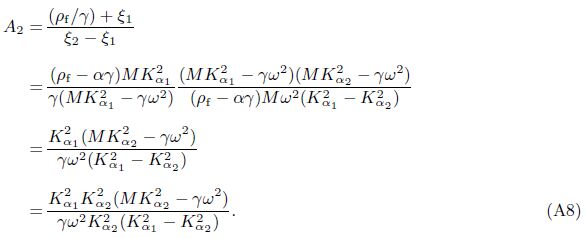

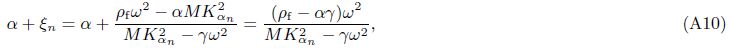
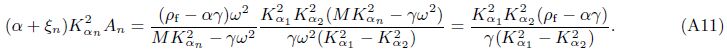
The solutions of Green’s functions deduced in the current paper differ in forms from the results obtained by Cheng et al.[4] ,but they are in fact identical.
We can define
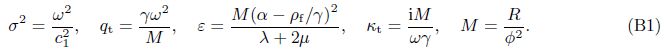
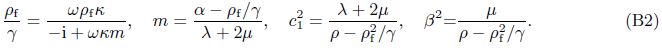
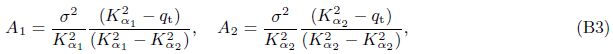
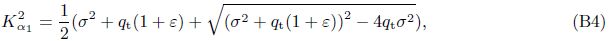
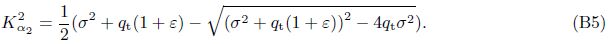
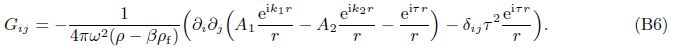
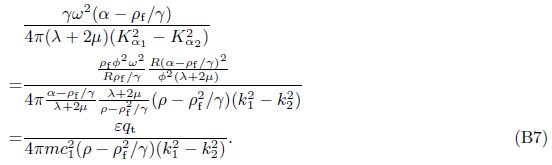
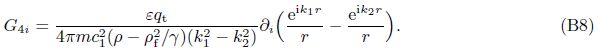
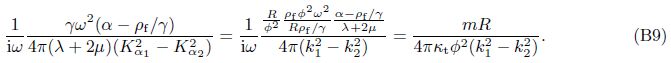
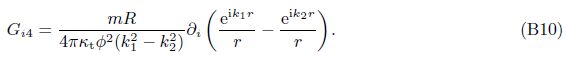
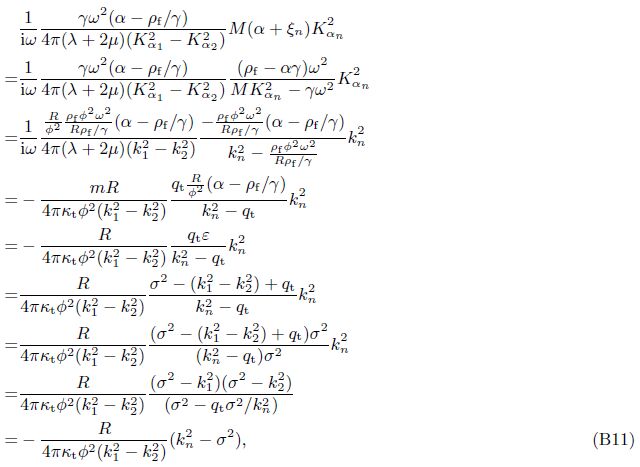
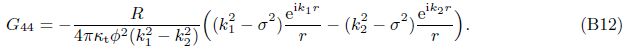
| [1] | Biot, M. A. Theory of propagation of elastic wave in a fluid-saturated soil, 1:low-frequency range, 2:higher frequency range. Journal of the Acoustical Society of America, 28, 168-191(1956) |
| [2] | Biot, M. A. Generalized theory of acoustic propagation in porous dissipative medium. Journal of the Acoustical Society of America, 34, 1254-1264(1962) |
| [3] | Deresiewicz, H. The effect of boundaries on wave propagation in a liquid-filled porous solid, part I:reflection of plane waves at a free plane boundary (non-dissipative case). Bulletin of the Seismological Society of America, 50, 599-607(1960) |
| [4] | Cheng, A. H. D., Badmus, T., and Beskos, D. E. Integral equation for dynamic poroelasticity in frequency domain with BEM solution. Journal of Engineering Mechanics, 117(5), 1136-1157(1991) |
| [5] | Sahay, P. N. Dynamic Green's function for homogeneous and isotropic porous media. Geophysical Journal International, 147, 622-699(2001) |
| [6] | Schanz, M. Dynamic fundamental solutions for compressible and incompressible modeled poroelastic continua. International Journal of Solids and Structures, 41, 4047-4073(2004) |
| [7] | Celebi, E. Three-dimensional modelling of train-track and sub-soil analysis for surface vibrations due to moving loads. Applied Mathematics and Computation, 1(179), 209-230(2006) |
| [8] | Galvín, P. and Domínguez, J. High-speed train-induced ground motion and interaction with structures. Journal of Sound Vibration, 307, 755-777(2007) |
| [9] | Lu, J. F., Jeng, D. S., and Williams, S. J. A 2.5-D dynamic model for a saturated porous medium, part Ⅱ:boundary element method. International Journal of Solids and Structures, 45, 359-377(2008) |
| [10] | Lu, J. F., Jeng, D. S., and Williams, S. J. A 2.5-D dynamic model for a saturated porous medium, part I:Green's function. International Journal of Solids and Structures, 45, 378-391(2008) |
| [11] | Plona, T. J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Applied Physics Letters, 36(4), 259-261(1980) |
| [12] | Ding, B. Y. Experimental study and theoretical analysis of seismic wave characteristics before the crack of cracks and pore medium. Northwestern Seismological Journal, Supplement 1, 18-33(1984) |
| [13] | Plona, T. J. and Johnson, D. L. Acoustic properties of porous systems, I:phenomenological description. AIP Conference Proceedings, 107, 89-104(1984) |
| [14] | Geertsma, J. and Smit, D. C. Some aspects of elastic wave propagation in fluid-saturated porous solids. Geophysics, 26, 169-181(1961) |
| [15] | Burridge, R. and Vargas, C. A. The fundamental solution in dynamic poroelasticity. Geophysical Journal of the Royal Astronomical Society, 58, 61-90(1979) |
| [16] | Mei, C. C. and Foda, M. A. Wave-induced responses in a fluid filled poro-elastic solid with a free surface-a boundary layer theory. Geophysical Journal of the Royal Astronomical Society, 66, 597-631(1981) |
| [17] | Norris, A. N. Radiation from a point source and scattering theory in a fluid saturated porous solid. Journal of the Acoustical Soeiety of America, 77, 2012-2023(1985) |
| [18] | Halpern, M. R. and Christiano, P. Response of poroelastic halfspace to steady-state harmonic surface tractions. International Journal for Numerical Analytical Methods Geomechanics, 10(6), 609-632(1986) |
| [19] | Manolis, G. D. and Beskos, D. E. Integral formulation and fundamental solutions of dynamic poroelasticity and thermoelasticity. Acta Mechanica, 76, 89-104(1989) |
| [20] | Philippacopoulos, A. J. Waves in a partially saturated layered half-space analytic formulation. Bulletin of the Seismological Society of America, 77(5), 1838-1853(1987) |
| [21] | Philippacopoulos, A. J. Spectral Green's dyadic for point sources in poroelastic media. Journal of Engineering Mechanics, 124(1), 24-31(1998) |
| [22] | Kaynia, A. M. and Banerjee, P. K. Fundamental solutions of Biot's equation of dynamic poroelasticity. International Journal of Engineering Sciences, 31(5), 817-830(1993) |
| [23] | Ding, B. Y. and Yuan, J. H. Dynamic Green's functions of a two-phase saturated medium subjected to a concentrated force. Internatioal Journal of Solids and Structures, 48, 2288-2303(2011) |
| [24] | Schanz, M. Poroelastodynamics:linear models, analytical solutions, and numerical methods. Applied Mechanics Reviews, 62(3), 030803(2009) |
| [25] | Ding, B. Y., Yuan, J. H., and Pan, X. D. The abstracted and integrated Green functions and OOP of BEM in soil dynamics. Science in China Serits G:Physics Mechanics and Astronomy, 51(12), 1926-1937(2008) |
| [26] | Ding, B. Y., Cheng, A. H. D., and Chen, Z. L. Fundamental solutions of poroelastodynamics in frequency domain based on wave decomposition. Journal of Applied Mechanics, 80(6), 061021(2013) |
| [27] | Chen, J. Time domain fundamental solution to Boit's complete equations of dynamic poroelasticity, part I. International Journal of Solids and Structures, 31(10), 1447-1490(1994) |
| [28] | Chen, J. Time domain fundamental solution to Boit's complete equations of dynamic poroelasticity, part Ⅱ. International Journal of Solids and Structures, 31(2), 169-202(1994) |
| [29] | De Hoop, A. T. Representation Theorems for the Displacement in an Elastic Solid and Their Application to Elastodynamic Diffraction Theory, Ph. D. dissertation, Delft University of Technology, (1958) |
| [30] | Manolis, G. D. A comparative study on three boundary element method approaches to problems in elastodynamics. International Journal for Numerical Methods in Engineering, 19(1), 73-91(1983) |
| [31] | Ding, B. Y., Ding, C. H., and Chen, Y. Green function on two-phase saturated medium by concentrated force in two-dimensional displacement field. Applied Mathematics and Mechanics (English Edition), 25(8), 951-956(2004) DOI 10.1007/BF02438804 |
 2016, Vol. 37
2016, Vol. 37





