1 Introduction

Non-Newtonian fluids have been a famous topic of research for their diverse use in many industrial processes, such as polymer solutions, blood, and heavy oils. These fluids have been modeled in a number of diverse manners with their constitutive equations varying greatly in complexity, among which the viscoelastic Maxwell fluid model has been studied widely^{[1, 2, 3]}. The Maxwell fluid has achieved some successes in describing polymeric liquids, in which case it is more amenable to analysis and more important to experiments.

The fractional calculus has been used successfully for describing behavior of viscoelastic fluids^{[4, 5]}. The first application of fractional derivatives was given by Abel who applied the fractional calculus in the solution of an integral equation. Bagley and Torvik^[6] showed that fractional calculus models of viscoelastic materials were in harmony with the molecular theory and obtained the fractional differential equation of order 1/2. The relaxation and retarda- tion functions were determined for the four-parameter Maxwell model by Friedrich^[7]. Song and Jiang^[8] used the fractional calculus to analyze the experimental data of viscoelastic gum and obtained satisfactory results. In general, the constitutive equations for generalized non- Newtonian fluids are modified from the well-known fluid models by replacing the time derivative

of an integer order with the so-called Riemann-Liouville fractional calculus operators. Qi and Xu^{[9, 10]} considered Stokes’ first problem and some unsteady unidirectional flows for a vis- coelastic fluid with the generalized Oldroyd-B model. Fetecau et al.^{[11, 12, 13, 14]} investigated some accelerated flows of a generalized Oldroyd-B fluid. Khan et al.^[15] studied the magnetohydro- dynamic (MHD) flow of a generalized Oldroyd-B fluid with modified Darcy’s law in a circular pipe. Zheng et al.^{[16, 17]} considered some MHD flows of the generalized viscoelastic fluid. Shen et al.^{[18, 19]} studied the decay of vortex velocity and diffusion of temperature in a generalized second grade fluid and a Reyleigh-Stokes problem for a heated generalized second grade fluid with the fractional derivative. Recently, some new energy constitutive equation models have been proposed by Ezzat^[20] and Qi and Liu^[21] who took the time fractional derivative into account, and the associated flow and heat transfer characteristics were analyzed. Jiang and Qi^[22] built a new fractional thermal wave model of the bioheat transfer and used it to examine the heat transfer in biological tissues. Xu and Jiang^[23] proposed a fractional dual-phase-lag model and the corresponding bioheat transfer equation. The inverse problem of estimating the fractional model parameters was also studied based on the non-linear least square method.

Motivated by the above-mentioned works, this paper considers a new model for the Fourier law of heat conduction with time-fractional order to the generalized Maxwell fluid. The flow is induced by a moving plane and influenced by the magnetic field, the radiation heat, and the heat source. We use the Laplace transform and solve the ordinary differential equations with the matrix form to obtain the velocity and temperature in the Laplace domain. In order to obtain solutions from the Laplace space back to the original space, we use the numerical inversion of the Laplace transform. Some graphs are presented for various parameters, and the corresponding flow and heat transfer characteristics are discussed.

2 Governing equations

The governing equations for an incompressible fluid are given by

where T is the Cauchy stress tensor, V is the velocity vector, ρ is the constant density of the fluid, and b is the body force field.

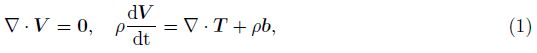
We consider that the fluid is permeated by an imposed magnetic field B₀ which acts in the positive x-direction. The Lorentz force with one component in the x-direction is

where σ₀ is the electrical conductivity, B₀ is the magnetic induction, k₀ is the Seebeck coefficient, and T is the absolute temperature, which is a function of the coordinate y and the time t.

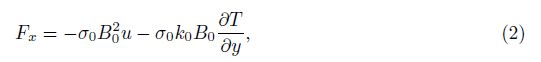
Assume the velocity and shear stress in the forms of

where u is the velocity, and i is the unit vector in the x-direction. Taking account of the initial condition S(y, 0) = 0, the motion equations of the generalized Maxwell fluid with modified Ohm’s law in the absence of the pressure gradient in the x-direction are where τ(y, t) = S_xy(y, t) is the shear stress that is nonzero, υ = μ/ρ is the kinematic viscosity, λ is a material constant, and D_t^α is the Riemann-Liouville fractional differential operator of the order α with respect to t defined as^{[4, 5]} where Γ(·) is the Gamma function.

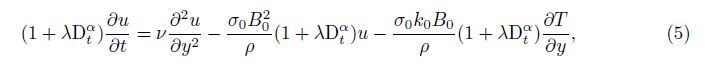
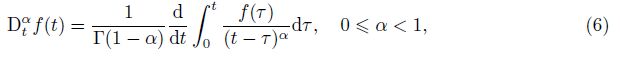
The energy equation in terms of the heat conduction vector q is

where c_p is the specific heat of a fluid at the constant pressure, φ is the internal heat, and the operator D/Dt is defined as The generalized Fourier law of the heat conduction including the current density effect and the radiation heat effect q_r can be considered as where kT is the thermal conductivity, λr is the relaxation time, П is the Peltier coefficient, and J is the conduction current density vector.

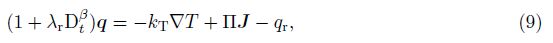
The generalized energy equation^{[16, 24, 25]} with the time fractional derivative of the order β (0 < β 6 1) is

With the Lorentz force F_x and the heat source Q(y, t), the energy equation is where π₀ is the Peltier coefficient at T₀, which is a reference temperature.

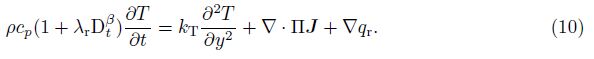
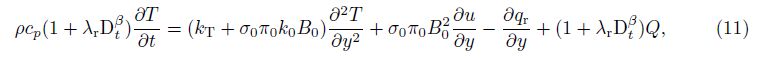
With the Rosseland approximation for the radiation, the radiation heat flux is simplified as^{[26, 27]}

where σ^∗ and k^∗ are the Stefan-Boltzmann constant and the mean absorption coefficient, re- spectively. We assume that the temperature difference within the flow is sufficiently small such that the term T⁴ can be expressed as a linear function of temperature. Hence, expanding T⁴ in a Taylor series about a free stream temperature T_∞ and neglecting higher-order terms yield It should be noted that the above radiation transfer pertains to an optically thick model.

In view of Eqs. (12) and (13), Eq. (11) reduces to

where N_R =$\frac{{{k^*}{k_T}}}{{4{\sigma ^*}T_\infty ^3}}$.

3 Flow due to uniformly accelerated plate

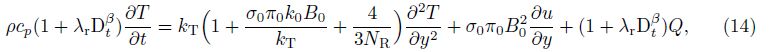
Consider an incompressible fractional Maxwell fluid lying over an infinitely extended plate which is situated in the xz-plane. Initially, the fluid is at rest, and at the time t = 0⁺, the infinite plate begins to slide in its own plane with a uniform acceleration Ut (U is a constant). Let T_w denote the temperature of the plate for t > 0. Suppose that the temperature of the fluid at the moment t = 0 is T_∞, and there is a plane distribution of continuous heat sources located at the plane y = 0. By the influence of shear, the fluid above the plate is gradually set in motion. Therefore, the governing equations will be of the forms of Eqs. (5) and (14).

To simplify the algebra, we introduce the following non-dimensional quantities:

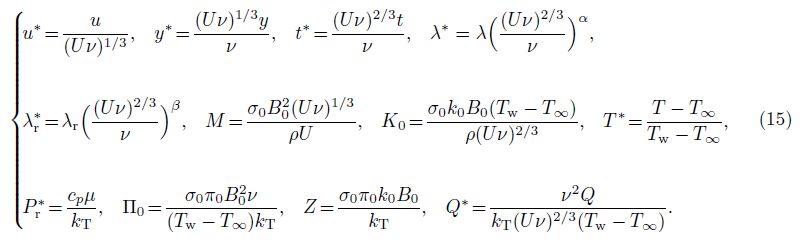
Dimensionless governing equations can be given (for brevity, the dimensionless mark “∗” is omitted here) as follows:

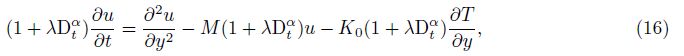
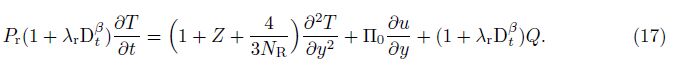
Here, we consider a heat source of the form Q = Q₀δ(y)H(t)(Q₀ is a constant). Initially, the dimensionless velocity is u(y, 0) = 0, and the temperature is T (y, 0) = 0. In order to solve the above problem, we use the Laplace transform principle of sequential fractional derivatives on both sides of Eqs. (16)-(17), and write the resulting equations in a matrix form of^{[28, 29, 30, 31, 32, 33, 34]}

where s is a transform parameter, C =$\frac{{{P_r}s(1 + {\lambda _r}{s^\beta })}}{{1 + Z + \frac{4}{{3{N_R}}}}}$, D =$\frac{{{\prod _0}}}{{1 + Z + \frac{4}{{3{N_R}}}}}$, and γ=$\frac{{1 + {\lambda _r}{s^\beta }}}{{1 + Z + \frac{4}{{3{N_R}}}}}$.

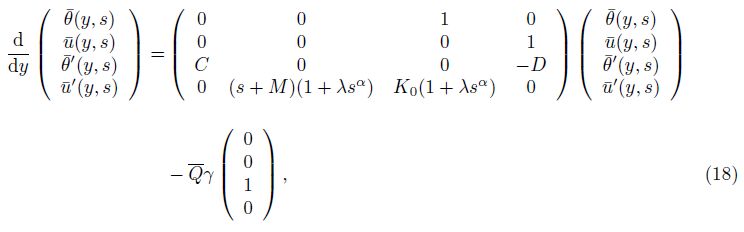
Equation (18) can be written in the constricted form as

where $\bar G$(y, s) denotes the state vector in the transform domain whose components consist of the transformed temperature, velocity, as well as their gradients.

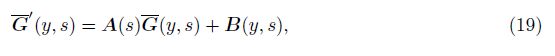
We shall use the well-known Cayley-Hamilton theorem to find the form of the matrix exp(A(s)y). The characteristic equation of the matrix A(s) can be written as

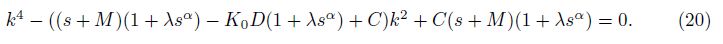
The roots of this equation, ±k₁ and ±k₂, satisfy the relations

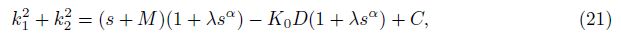
The Taylor series expansion of the matrix exponential in exp(A(s)y) has the form

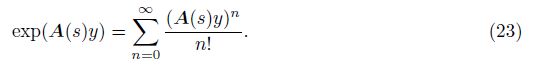
Using the Cayley-Hamilton theorem, we can express A₄ and all higher powers of A in terms of A₃, A₂, A, and I, where I is the unit matrix of order 4. The matrix exponential can now be written in the form of

where a₀, a₁, a₂, and a₃ are coefficients depending on y and s, which leads to the following equations:

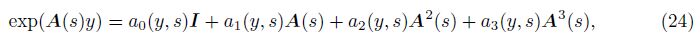
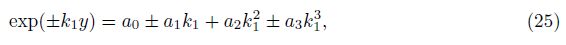
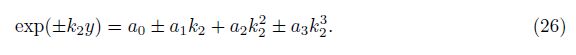
The solutions of the above system are given by

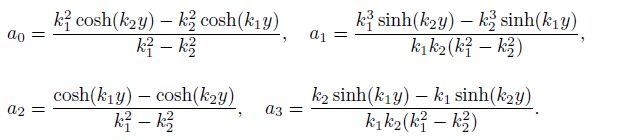
Hence, we have

where the elements l_ij (y, s) are given in Appendix A.

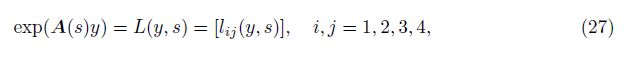
In the actual physical problem, the space is divided into two regions accordingly as y > 0 and y ≤ 0. Inside the region 0 ≤ y < ∞, the positive exponential terms are not bounded at infinity. Thus, for y > 0, we replace each sinh(ky) and cosh(ky) by −exp(−ky)/2 and exp(−ky)/2, respectively. In the region y 6 0, the negative exponential terms are suppressed instead.

The formal solution of Eqs. (19) can be written in the form of

where $\bar G$(0, s) $\left({\begin{array}{*{20}{c}}{\bar \theta (0, s)}\\{\bar u(0, s)}\\{\bar \theta '(0, s)}\\{\bar u'(0, s)} \end{array}} \right)$.Using the integral prosperities of the Dirac delta function, we obtain where

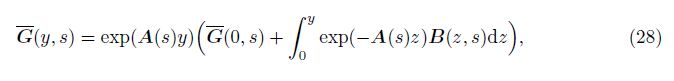
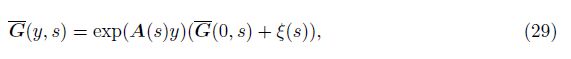
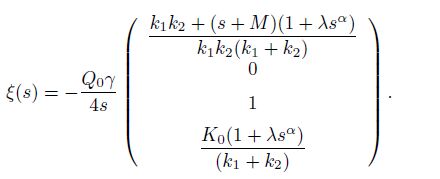
Initially, the plate is at rest. At t > 0, the plate moves with the velocity t, and we have

For the heat source located in y = 0, the temperature is symmetric with respect to y. Then, Use Fourier’s law of heat conduction in the non-dimensional form, namely,

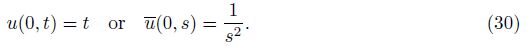
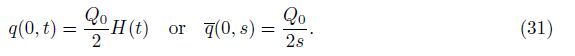
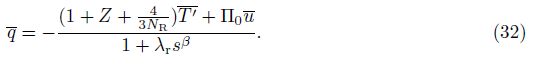
Thus, we obtain the condition

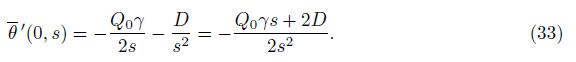
Equations (30) and (33) are two components of the initial state vector $\bar G$(0, s). To obtain the remaining two components, we substitute y = 0 on both sides of Eq. (29) to obtain the following two solutions:

Substituting the above equations into the right-hand side of Eq. (29), we obtain This completes the solution in the Laplace domain.

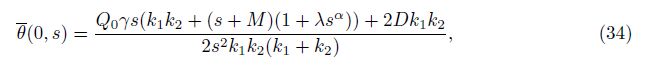
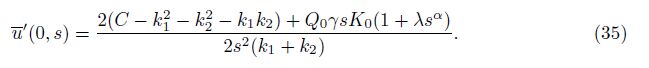
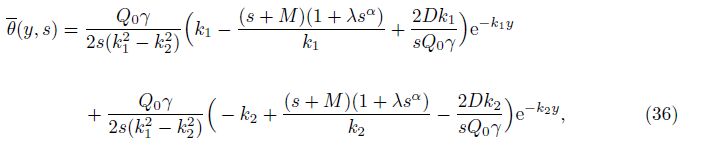
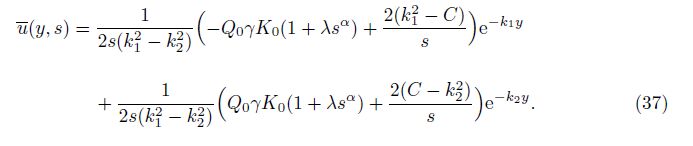
In order to invert the Laplace transform in the above equations, we adopt a numerical inversion method based on a Fourier series expansion^[35] as follow:

where F(v) is the Laplace transform of f(t), v > 0 is an arbitrary constant, and N is sufficiently large integer.

4 Flow due to variably accelerated plate

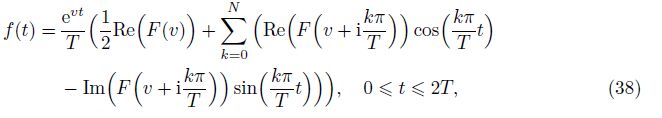
Here, the fluid and the plate are considered at rest for t 6 0, and the infinitely extended plate starts to move in its own plane with the variable acceleration Vt² (V is a constant). The governing equations, the initial and a part of the boundary conditions are the same. In this case, we replace the first equation of (30) as follows:

Here, the non-dimensional quantities are

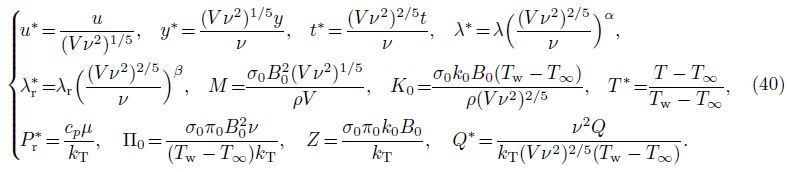
The non-dimensional governing equations are Eqs. (16)-(17), and the initial condition of the velocity field in the Laplace domain is $\bar u$(0, s) = 2/s³.

Adopting a similar procedure as before, we have

We obtain the expressions for the velocity field and the temperature field in the transform plane as follows:

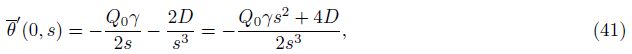
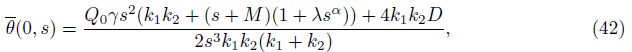
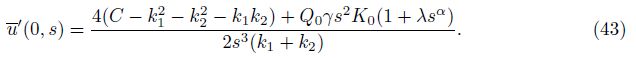
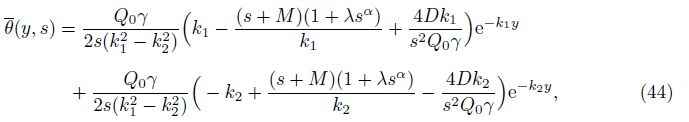
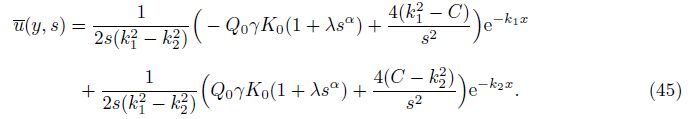
This completes the solution in the Laplace domain. Now, we obtain the solution in the original space by performing the inverse of the Laplace transform numerically using Eq. (38)^[35].

5 Results and discussion

In Sections 3 and 4, we consider the flow of a Maxwell fluid with the uniform acceleration boundary condition and the variable accelerating boundary condition, respectively. Graphical results show the velocity profiles and the temperature profiles for different values of M, N_R, α, β, and Q₀.

Figures 1 and 2 show the velocity changes with the fractional parameters α and β at the time t = 5. It is clearly seen that the smaller the values of α and β are, the more steadily the velocity changes. The boundary layer region around the surface is dependent on the fractional order α. The fractional parameter β has the quite opposite effect to α. Figures 3 and 4 are the temperature profiles for fractional parameters α and β, which have the same effect as the velocity profile. Figures 5 and 6 depict the influence of the magnetic body for the velocity field and the temperature field. As expected, the magnetic force M is favorable to the decay of the velocity, and the temperature profiles have a marked decrease with the increase in M. This is due to the fact that the applied transverse magnetic field produces a drag in the form of the Lorentz force, thereby decreasing the magnitude of velocity. Figures 7-10 demonstrate the influence of N_R and Q₀ for the velocity field and the temperature field. It is clear that near the plate, the velocity and temperature increase with the increasing radiation heat effect NR and heat source Q₀. The increase of the temperature results in the increasing velocity. As the radiation heat is a radiating process, the radiation parameter increases, and the temperature decreases rapidly in the y-direction. Figures 11-Figures 20 are plotted to demonstrate the effects of different parameters on the velocity and temperature fields by using the solution obtained in Section 4. As the plane is moving with the variable acceleration V t₂ with the increasing timet, the velocity and temperature are increasing remarkably.

6 Conclusion

The purpose of this paper is to introduce a new model for the Fourier law of heat conduction with the time-fractional order to a generalized Maxwell fluid. The motion equation and energy equation are coupled with each other. We use the Laplace transform and numerical inverse Laplace transform to analyze the velocity field and temperature field. The effect of increasing the magnetic force M is to decrease the velocity and temperature. However, the effect of heat source Q₀ has the opposite effect, and increasing the radiation heat N_R can decrease the temperature rapidly. This fluid is related to the magnetic field, the radiation heat effect, and the heat source, which plays an important role in engineering, petroleum industries, and heat transform.