Nomenclature

u,v,w,velocity components/(m·s−1);	A,unsteadiness parameter;
x,y,z,direction components;	S,ratio parameter;
U0,V0,reference velocities/(m·s−1);	Pr,Prandtl number;
L,characteristics length/m;	Ec,Eckert number;
g,acceleration due to gravity/(m·s−2);	M,Hartman number;
k∗,thermal conductivity /(W·K−1·m−1);	K,porosity parameter;
cp,specific heat/(m2·s−2);	Cfx,Cfy,local skin friction coefficients;
T,temperature/K;	qw,surface heat flux/(W·m−2);
T∞,ambient fluid temperature/K;	Nux,local Nusselt number;
Tw,surface temperature;	Rexy,local Reynolds number;
T0,reference temperature;	B0,uniform magnetic field;
Uw,Vw,stretching surface velocities;	f0,g0,initial approximations for ve-locity;
S,ratio parameter;	Ci(i = 1,2,· · · ,8),constants;
k,porous medium permeability;	q,embedded parameter;
α1,α2,α3,velocity and thermal slip fac-tors;	f∗,g∗,particular solution for veloc-ity field.

Greek symbols

σ,thermal diffusivity/(m2·s−1);	L1,L2,L3,linear operators for velocity and temperature;
ρ,density/(kg·m−3);	Rmf,Rmg,Rmθ,mth-order nonlinear operators;
μ,viscosity/(kg·m−2·s−1);	ħf ,ħg,ħθ,non-zero auxiliary parameters;
θ,dimensionless temperature;	θ0,initial approximation for temperature;
η,transformed coordinate;	θ∗,particular solution for temperature field.
γ1,γ2,γ3,velocity and thermal slip pa-rameters;
τxz,τyz,τ,wall shear stresses;

Subscripts

w,f,∞,represents conditions at wall,fluid and in free stream,respectively;	p,constant pressure;
	m,mth-order derivative with respect to η.

Superscripts:

′,prime represents derivative with respect to η.

1 Introduction

Boundary layer flows by a stretching surface have importance in the process of extrusion, crystal growth,glass-fiber,electronic chips,paper production,etc. Sakiadis^[1] first explored behavior of viscous fluid due to a moving surface. Flows in porous media also arise in several industrial processes. In addition,such flows contribute to widespread industrial applications and many natural phenomena which exist in the field of geothermodynamics for the energy recovery, grain storage,storage thermal energy,chemical catalytic reactors,oil extraction,solar power collectors,regenerative heat exchangers,flow through filtering devices,electrochemical process, food processing,cooling of electronic compartments,packed-bed reactors,casting and welding during manufacturing processes,soil pollution,and fibrous insulation,etc. The investigation of flow and heat transfer through porous media is further significant particularly in contemporary technologies where the boundary-layer control is important. Porous materials were used to enhance the rate of heat transfer from stretching surfaces^[2]. Mandal and Mukhopadhyay^[3] numerically analyzed the boundary layer flow with the heat transfer towards a porous stretched surface saturated with the porous medium. The variable heat flux at the surface is taken. The analytic solution for the flow of micropolar fluid in the presence of thermal radiation was developed by Rashidi et al.^[4]. Here,the fluid saturates the porous medium. Sheikholeslami et al.^[5] performed an analysis to scrutinize the boundary layer flow of nanofluid over a permeable stretched wall. Four different types of nanoparticles with water as the base fluid in a porous medium are considered. Hayat et al.^[6] reported the steady magnetohydrodynamic (MHD) flow of nanofluid over a stretching surface saturated with a porous medium. The problem of mixed convection flow by an inclined flat surface through the porous medium was discussed by Rashidi et al.^[7]. Hatami and Ganji^[8] used the least square method for the development of flow analysis in microchannel heat sink (MCHS) cooled by Cu-water nanofluid with thermal effects. Parand et al.^[9] carried out the analysis for heat transfer equations in a porous medium. The two-dimensional MHD stagnation point flow towards a radiating stretching surface through a porous medium was investigated by Hayat et al.^[10] in the presence of buoyancy effects. The flow of an incompressible Jeffery fluid saturating a porous medium was investigated by Hayat et al.^[11].

It should be noted that no-slip conditions are employed in all the above mentioned attempts. However,in a microelectro mechanical system and some coated surfaces (such as Teflon,re- sist adhesion),the no-slip boundary condition is not valid. Hence,the slip phenomenon must be considered. The fluids with the slip phenomenon at the boundary have significant techno- logical applications including polishing of artificial heart valves and internal cavities. Many models have been proposed for analyzing the slip effect at solid boundaries. The slip flow model describes a relation between the tangential component of the velocity at the surface and the velocity gradient normal to the surface. Thus,a new dimension is added to the above mentioned study by considering the effects of partial slip at the stretching wall. Many re- searchers at present have focused on the flow and heat transfer analysis at micro-scale with slip effects. Turkyilmazoglu^[12] obtained multiple solutions for the heat and mass transfer anal- ysis of viscoelastic fluids due to a stretching surface with slip conditions. Freidoonimehr et al.^[13] presented the MHD stagnation point flow towards a porous rotating surface with the velocity slip condition. Turkyilmazoglu^[14] performed an analysis to study the characteristics of heat and mass transfer in the viscous flow towards a stretching surface with velocity and thermal slip conditions. Mukhopadhyay^[15] studied the slip effects in MHD flow past a porous stretchable surface with the thermal radiation. Malvandi et al.^[16] numerically investigated the two-dimensional stagnation point flow of a nanofluid induced by a stretchable sheet with Navier’s slip condition. Turkyilmazoglu^[17] considered the MHD slip flow of an electrically conducting non-Newtonian fluid towards a shrinking surface. The slip effect in the mixed con- vective boundary layer flow over a flat plate was reported by Bhattacharyya et al.^[18]. Rashidi et al.^[19] numerically presented the effects of magnetic,slip,and relative temperature difference on the velocity and temperature field in the flow by a rotating disk. The entropy generation with variable properties over a rotating disk was also analyzed. Mukhopadhyay^[20] examined the MHD axisymmetric flow of a viscous fluid by a stretched cylinder heat transfer. The partial slip effect was studied by the flow analysis.

The motivation of the present study is to analyze the effects of velocity and thermal slip conditions in the unsteady three-dimensional flow by an exponential stretchable sheet. The fluid is electrically conducting with the magnetic field. The relevant formulation for the con- sidered problems is made. Analytical solutions are developed by utilizing homotopy analysis method^{[21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32]}. The effects of the velocity,temperature,coefficient of skin friction,and Nusselt number have been determined for various physical parameters.

2 Problem formulation

Consider the unsteady three-dimensional flow of the viscous and electrically permeable fluid induced by a stretching surface. The fluid saturates the porous medium. It is assumed that the sheet is stretched along the η-plane,while the fluid is placed parallel to the z-axis. Moreover,a magnetic field of uniform strength B₀ is applied. The assumption of very low magnetic Reynolds number is considered to neglect the induced magnetic field. Here,we assume that the sheet has stretched with the linear velocities u = and v = in the xy-plane,respec- tively. With the application of the velocity V = [u(x,y,z,t),v(x,y,z,t),w(x,y,z,t)] and the temperature T = T (x,y,z,t),the governing three-dimensional boundary layer equations are

Here,u,v,and w denote the velocity components corresponding to x-,y-,and z-directions, respectively,ρ represents the fluid density,υ is kinematic viscosity,σ represents the electrical conductivity of fluid,c_p represents the specific heat,T represents the temperature of fluid,k∗ represents the thermal conductivity,and k represents the porous medium permeability. The associated conditions at the wall can be expressed as in which U_w and V_w are the stretching velocities,T_w is the surface temperature,T₀ is the reference temperature,T_∞ is the ambient temperature,α1 and α2 are hydrodynamic slip factors, and α3 is the thermal slip factor. These slip factors are of the dimension of length.

With the consideration of the following dimensionless variables:

the governing transformed equations can be written as follows: in which prime denotes the differentiation with respect to the similarity variable η,A represents the unsteadiness parameter,S represents the ratio parameter,M represents the Hartman num- ber,K represents the porosity parameter,Pr represents the Prandtl number,Ec represents the Eckert number, γ1 and γ2 are the velocity slip parameters,and γ3 is the thermal slip parameter. Values of these parameters are The coefficients of the skin friction C_fx,C_fy and the local Nusselt number N_ux are in which the expressions of the skin friction at the wall (τ_w) and the heat flux at the wall (q_w) are given by  Using Eq. 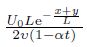(5),we have where Re_xy = denotes the local Reynolds number.

3 Solutions derivation

For series solutions by the homotopic technique,we choose the base functions for velocity and temperature fields,which are expressed as

with where a_m,n^k,b_m,n^k,and c_m,n^k are the arbitrary constants. We have chosen the following initial guesses f₀(η),g₀(η),θ0(η) and the auxiliary linear operators Li (i = 1,2,3) : The chosen auxiliary linear operators satisfy the following properties: ` in which C_i (i = 1,2,· · · ,8) are the arbitrary constants.

3.1 Zeroth-order deformation problems

The zeroth-order deformed problems can be put into the forms

The above expressions q ∈ [0, 1] and ħ_f ≠ 0, ħ_g ≠ 0, ħ_θ ≠ 0 represent the embedded and auxiliary parameters,respectively. The non-linear operators are given by In the form of Taylor series,we can write The convergence of the series (33)-(35) is strictly based upon ħ_f ,ħ_g,and ħ_θ. The values of ~f ,ħ_g,and ħ_θ are chosen in such a way that the series (33)-(35) show convergent behavior at q = 1,and hence

3.2 mth-order deformation problems

The mth-order deformation problems are

where  The general solutions corresponding to mth-order deformation problems are The above expressions f^∗,g^∗,and θ^∗ represent the particular/special solutions,and C_i (i = 1,2, · · · ,8) denote the arbitrary constants.

4 Convergence of homotopic solutions

The auxiliary parameters ħ_f ,ħ_g,and ħ_θ are highly responsible for convergence of analytical solutions obtained by the homotopy analysis method. To achieve the permissible numerical values of auxiliary parameters,the so-called ħ-curves are plotted at 18th-order of approximation in Fig. 1. The allowable values of ħ_f ,ħ_g,and ħ_θ lie along the line parallel to ħ_f -,ħ_g-,and ħ_θ- axes. Ranges for admissible values of ħ_f ,ħ_g,and ħ_θ are −0.7≤ħ_f≤−0.2,−0.7≤ħ_g≤−0.1, and −0.75≤ħ_θ≤−0.1.

5 Results and discussion

The objective here is to analyze the impact of different pertinent physical parameters on the distributions of velocities and temperature. Figure 2 shows the characteristics of unsteadiness parameter A on the horizontal velocity component f′(η). Here,the velocity profile shows de- creasing behavior for larger values of A. The further momentum boundary layer is thinner for the larger unsteadiness parameter. The effect of permeability parameter K on the velocity field is displayed in Fig. 3. The Velocity profile and the associated thickness of the boundary layer increase for the larger permeability parameter. Behavior of the Hartman number M on the horizontal velocity component f′(η) is sketched in Fig. 4. The velocity profile is a decreasing function of the Hartman number M. For larger values of the magnetic parameter,the Lorentz force enhances,leading to more resistance to the motion of fluid,and hence a reduction of the velocity distribution. Figure 5 is illustrated to view behavior of ratio parameter S on the component of velocity profile f′(η). Here,both the velocity and thickness of the momentum boundary layer decrease for S = 0,0.4,0.8,1.3. Obviously,an increment in S measures the stretching velocity component in the y-direction dominant over the x-component of velocity, and as a result,f′(η) shows decreasing behavior. The effects of the velocity slip parameter 1 on the velocity profile f′(η) are demonstrated in Fig. 6. It is reported that horizontal ve- locity component and momentum thickness boundary layer are smaller with an increment in 1. Clearly,for higher values of velocity slip parameter ( 1),the stretching velocity is partially transferred to the fluid,and consequently the velocity profile decreases. Figure 7 illustrates the impact of velocity slip parameter γ2 on the velocity field f′(η). The velocity distribution and the associated thickness of the boundary layer increase for the larger velocity slip parameter γ2. The analysis of unsteadiness parameter A on the velocity profile g′(η) is examined in Fig. 8. Similar behavior has been noticeable for g′(η),as shown in Fig. 2. Figure 9 is exemplified for the variation of permeability parameter (K) on the distribution of velocity component g′(η). It is revealed that the velocity field g′(η) is lower for higher K. Figure 10 shows behavior of magnetic parameter M on the velocity profile g′(η). Obviously,the higher magnetic parameter results in the reduction of boundary layer thickness. Figure 11 gives the insight for the effect of ratio parameter S on the component of velocity g′(η). It is analyzed that higher values of S result in the increases with of velocity and the associated boundary layer. The increment in the parameter S leads to the fact that the velocity field in the y-direction has higher im- pact than the reference velocity in the x-direction. Therefore,the component of velocity g′(η) increases. The effect of velocity slip parameter γ1 on the velocity component g′(η) is demon strated in Fig. 12. The velocity profile g′(η) increases with the velocity slip 1. The momentum boundary layer is also increased. Behavior of slip parameter γ2 on the velocity profile g′(η) is demonstrated in Fig. 13. Both the velocity and the associated thickness of boundary layer are decreased for higher values of slip parameter γ2. In fact,for the increment in the velocity slips parameter γ2,the stretching velocity is partially transferred to the fluid,and thus the velocity field decreases.

The impact of unsteadiness parameter A on the temperature profile θ(η) is demonstrated in Fig. 14. The temperature distribution has decreasing behavior for the higher unsteadiness parameter A. Figure 15 demonstrates the impact of permeability parameter (K) on the tem- perature profile θ(η). The temperature profile θ(η) is an increasing function of K. The char- acteristics of magnetic parameter M on the temperature profile θ(η) is plotted in Fig. 16. The temperature distribution increases with an increment in M. Physically,for the increment in the magnetic parameter M,the Lorentz force enhances,which offers more resistance to the fluid flow. Hence,more heat generates,which results in the enhancement of temperature field θ(η). Figure 17 displays the influence of α on the temperature distribution. It is evident that the thickness of the thermal boundary layer and the temperature profile decrease when α increases. Behavior of the ratio parameter S on the temperature profile is shown in Fig. 18. The temperature distribution shows decreasing behavior when the ratio parameter S is increased. Further, the thickness of thermal boundary layer also diminishes. Figure 19 illustrates the effects of velocity slip parameter γ1 on the temperature field θ(η). It is analyzed that the temperature increases with increasing 1. The effect of velocity slip parameter γ2 on the distribution of temperature is demonstrated in Fig. 20. Here,we note that the temperature profile shows in- creasing the effects for the larger velocity slip parameter γ2. Figure 21 is drawn to see the effects of thermal slip parameter γ3 on the temperature field γ3. The temperature field decreases for larger values of thermal slip parameter 3. The incremented values of thermal slip parameterγ3 show a decrease in the rate of heat transfer from the surface to the adjacent fluid. Hence, the temperature of the fluid decreases. The variation of Pr on θ(η) is illustrated in Fig. 22. The temperature field shows increasing behavior for small values of Pr. When Pr increases, the thermal diffusivity decreases,and as a result the temperature reduces. Figures 23 and 24 indicate the effects of A and M on Re_xy^1/2 C_fx and Re_xy^1/2 C_fy. It is concluded that both Re_xy^1/2 C_fx and Re_xy^1/2 C_fy increase when A and M are increased. Figure 25 is plotted to see the influence of heat transfer rate Re_x^-1/2 N_ux for the parameters A and M. The higher rate of heat transfer is achieved in the absence and presence of the porous medium. Figure 26 is plotted to see the influence of heat transfer rate Re_x^-1/2 N_ux for the parameters A and Pr. The higher rate of heat transfer is achieved in the absence and presence of the porous medium.

Table 1 represents the convergence analysis for the system of series solutions. It is noted that 13th-order of approximations for f′′(0),10th-order of approximations for g′′(0),and 15th- order of approximations for θ′(0) are sufficient for the convergence. Table 2 presents behavior of coefficients of skin friction f′′(0) and g′′(0) for various physical parameters. It is noted that f′′(0) and g′′(0) increase for larger values of A,M,and S,while they decrease when K, 1,andγ2 are increased. Negative values of the skin friction coefficients represent that the drag force is exerted by the surface on the fluid. Skin friction coefficients can be reduced for smaller values of S,A,and M. Table 3 displays the effect of pertinent parameters on the Nusselt number. The higher Nusselt number is noted for larger values of A,K,α,S,and Pr. However,M, γ1,γ2,and γ3 reduce the Nusselt number. The comparison of Nusselt number with the published work obtained by Liu et al.^[33] is presented in the Table 4. The previously published data and the present results match well,which enhances the validity of the obtained results.

6 Conclusions

The three-dimensional MHD flow of viscous fluid by an exponentially stretched surface embedded in a porous medium is studied. Both velocity and thermal slip conditions are taken into account. The key points of this work are mentioned below.

The velocity component f′(η) decreases while g′(η) increases with the velocity slip parameter γ1. The unsteadiness parameter A has similar behavior for the velocity components f′(η) and g′(η),whereas opposite behavior is noted for the temperature. An increment in the value of Prandtl number diminishes the thickness of thermal boundary layer,and at the bounding surface,the rate of heat transfer enhances. Velocity profiles f′(η) and g′(η) decrease,and the temperature profile increases with the magnetic parameter. The thermal slip causes a reduction in the temperature field and the associated thickness of thermal boundary layer. The temperature profile is an increasing function of K,M, γ1,and γ2. The skin friction coefficients are smaller for higher values of K,γ1,and γ2.