1 Introduction

We shall consider exact solutions of the magnetohydrodynamic (MHD) equations^{[1, 2, 3]}

where u = (u₁,u₂,· · · ,u_N)^T,v = (v₁,v₂,· · · ,v_N)^T,and p = p(x,y,t) represent the unknown velocity field,the magnetic field,and the pressure,respectively,and υ = (υ1,υ2,· · · ,υN) and η = (η1,η2,· · · ,ηN) are parameters. In Eqs. (1)-(3),some notations are used for simplification in context. The inner product between two vectors is defined by u·v = u₁v₁+u₂v₂+· · ·+u_Nv_N, and the Hadamard product between two vectors is defined by u ∗ v = (u₁v₁,u₂v₂,· · · ,u_Nv_N).

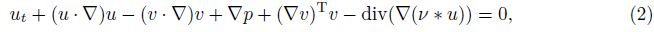
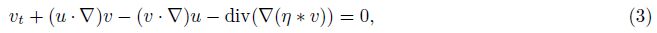
The dynamics of fluids in electromagnetic fields such as plasma,liquid metals,and salt water can be described by the MHD equations. Such flows may arise both in laboratory and astrophysical situations and can be often assumed to have an axial symmetry. This system is of interest for various reasons. For example,it includes some known equations,such as incompressible Navier-Stokes equations for v = 0^{[4, 5, 6, 7]},and incompressible Euler equations for v = 0,υ = 0^[8]. Therefore,the study of systems (1)-(3) can help the understanding of the Navier-Stokes equations and the Euler equations. A set of exact analytical solutions of the axisymmetric MHD equations was given for stationary and incompressible flows^[9]. Global existence of strong solutions of the regularized MHD system was proved^[10]. The regularity criteria to the 2D generalized MHD equations with zero magnetic diffusivity were considered^[11]. However,due to the complexity of MHD equations,it is still difficult to find exact solutions for general time-dependent MHD equations.

The purpose of this paper is to find a sufficient and necessary condition for existence of a class of vector exact solutions of time-dependent MHD equations (1)-(3) as follows:

where the N-dimensional vector functions a(t) and b(t) and the N × N matrix functions A(t) and B(t) are defined by and the elements a_i(t),b_i(t),a_ij (t),and b_ij(t) (i,j = 1,2,· · · ,N) are functions about t. Based on the algebraic technique on vectors,matrices,and curve integration,we theoretically show existence of the vector solutions (4) for the general N-dimensional incompressible MHD equa- tions. Such solutions are global and can be explicitly expressed by appropriate formulae,from which we find a series of exact solutions previously unknown.

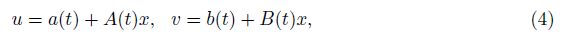
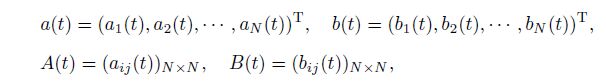
This paper is arranged as follows. In Section 2,we present a main result to show that the N-dimensional incompressible MHD equations admit the Cartesian solutions. Some illustrative examples are provided in Section 3 as applications of the main result.

2 Main results

Our main results on existence of solutions are stated as follows. Theorem 1 If the matrices A,B,and C = (A_t + A₂ + B^TB − B²B)/2 satisfy

then the N-dimensional incompressible MHD equations (1)-(3) admit explicit exact solutions in the forms of where c(t) is an arbitrary function of time variable t,at is the derivative of the function a(t) with respect to the variable t,and the trace of matrix A is defined by Proof We only need to verify that the functions (7) and (8) satisfy the MHD systems (1)-(3) under conditions (5)-(6). Substituting (7) into (1) gives In the same way,we have Substituting (7) into (3) yields which implies that We prove how to get the solution (8) through solving Eq. (2). Substituting (7) into (2) produces For the simplicity of expressions,we introduce an auxiliary matrix and rewrite Eq. (12) into the form of components In order to solve p(x) from Eq. (13),these N equations should be compatible with each other, that is,the vector functions (Q1,Q2,· · · ,QN) should constitute a potential filed of scalar field p,whose sufficient and necessary conditions are which holds if and only if This condition means that C is a symmetric matrix,which together with Eq. (10) gives the condition (5).

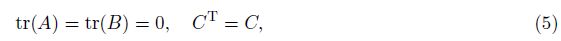
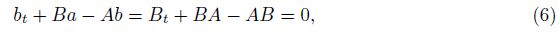
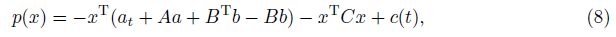
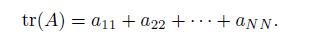
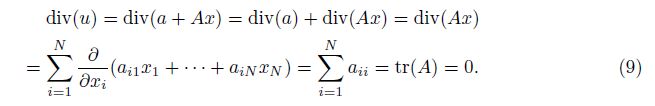
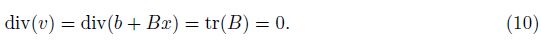
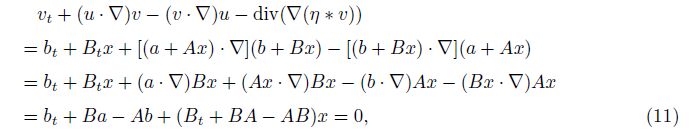
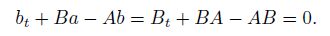
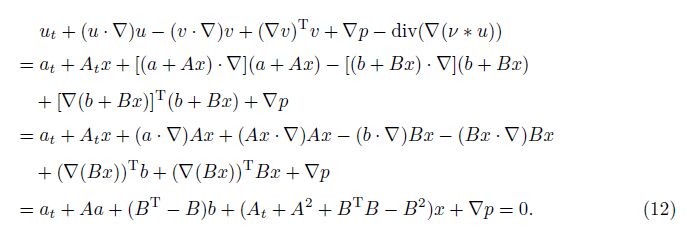
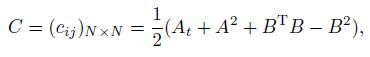
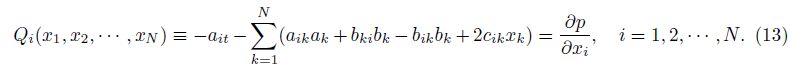
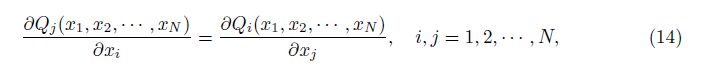
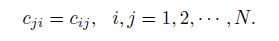
It follows from the condition (14),the function p is a complete differential,that is,

Therefore,the second kind of curvilinear integral of p(x) is independent of its integration route. In this way,we can take the special integration route and directly obtain Therefore,we have proved existence of the solutions (7) and (8) for N-dimensional MHD equa- tions (1)-(3).

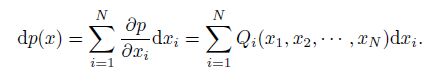
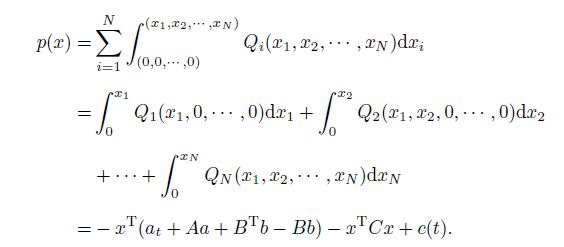
Remark 1 From (10) and (14) in the proof of this theorem,we may find that the conditions (5)-(6) actually are sufficient and necessary conditions for existence of solutions (7)-(8).

Remark 2 For the linear solution (4),it naturally holds that

which corresponds to the nonviscous case of the MHD equations (1)-(3). Therefore,Theorem 1 holds for both viscous MHD equations and inviscid MHD equations.

3 Applications

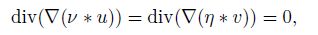
Let us consider the 2D MHD equations as a special case of Theorem 1. Example 1 Let

where a₁₁(t),a₁₂(t),b₁₁(t),b₁₂(t),a₁(t),a₂(t),b₁(t),and b₂(t) are functions to be determined. Therefore,the conditions (5)-(6) are satisfied. It is obvious that and Therefore,the condition (5) is directly satisfied. Substituting (15) into the second equation of (6) leads to which has a general solution A class of exact solutions for N-dimensional incompressible magnetohydrodynamic equations 213 where c₁,c₂ are two arbitrary constants,and a₁₁,a₁₂ are two arbitrary functions of t. With A and B so obtained,from the first equation,we take where b is an arbitrary vector function with respect to t.

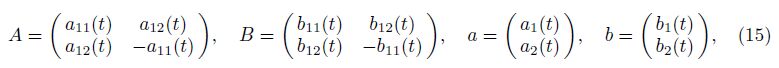
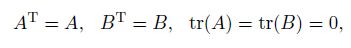
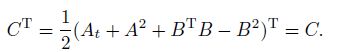
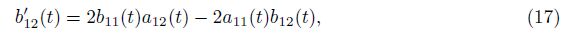
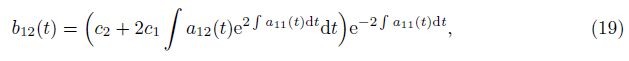
Specially,we take

Then,we get a solution

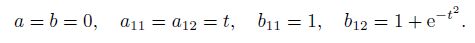
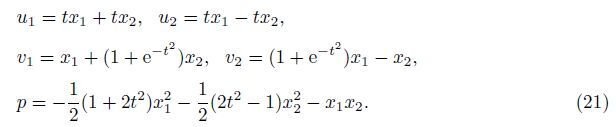
As a special case of Theorem 1,we give a simple corollary. Corollary 1 If the symmetric constant matrices A,B satisfy

and the vector functions a(t),b(t) satisfy then the incompressible MHD equations (1)-(3) admit the solutions (7)-(8).

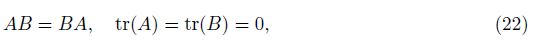
Proof It is easy to verify that the conditions (5)-(6) in Theorem 1 are satisfied under the conditions (22)-(23). Therefore,the incompressible MHD equations (1)-(3) admit the solutions (7)-(8).

From this corollary,we just take a,b,A,and B to satisfy Corollary 1,then,all functions (7)-(8) are solutions of the incompressible MHD equations (1)-(3). There are infinite such solutions to be directly constructed very easily. Let us see an example.

Example 2 As a special case of Corollary 1,set

Then,formulae (7)-(8) immediately give the rotational solutions for the 3D incompressible MHD equations where c(t) is an arbitrary function about t.

4 Concluding remarks

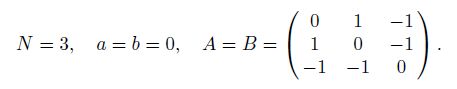
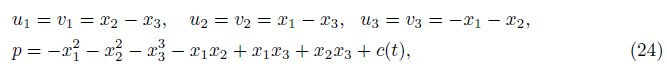
In this paper,based on algebraic techniques of vectors,matrices and curve integration,we have found necessary and sufficient conditions for existence of vector solutions for the general N- dimensional incompressible MHD equations. Among the solutions,to the best of our knowledge, some should be previously unknown. In addition,for incompressible MHD equations,the obtained solutions are still of linear forms about the spatial variable x. Therefore,a natural question is for the appropriate p,whether we could find solutions u,v in the nonlinear form about x. This question is difficult and worthy to be considered.