Nomenclature

C,solute concentration;	p,pressure;
Rm,basic density Rayleigh number;	g,acceleration due to gravity;
K,permeability of medium;	Le,thermo-solutal Lewis number;
d,depth of fluid layer;	Ln,thermo-nanofluid Lewis number;
kT,porous medium’s effective thermal conductivity;	NA,modified diffusivity ratio;
km,porous medium’s thermal diffusivity;	NB,modified nanoparticle-density increment;
Ra,thermal Rayleigh-Darcy number;	NCT,Soret parameter;
Rn,nanoparticle concentration Rayleigh number;	NTC,Dufour parameter;
Rs,solute concentration Rayleigh number;	T,temperature of the nanofluid;
Ta,Taylor’s number;	Tc,upper wall’s temperature;
DT,thermophoretic diffusion coefficient;	Th,lower wall’s temperature;
DB,Brownian diffusion coefficient;	t,time;
	v,velocity of the nanofluid.

Greek symbols

μ,fluid viscosity;	βT,thermal volumetric coefficient;
ρf ,fluid density;	βC,solutal volumetric coefficient;
ρp,nanoparticle mass density;	ε,porosity of the medium;
γ,thermal capacity ratio;	ψ,stream function;
Φ,volume fraction of the nanoparticle;	α,wave number;
	ω,frequency of oscillations.

Subscripts

f,fluid;	p,particle.
b,quiescent solution;

Superscripts

′,perturbed variable;

∗,dimensional variable.

Operators

1 Introduction

The current persisting scenarios of the industries,including the transportation,heating,ventilating, and air conditioning,paper and textiles,geothermal energy extraction,have started using nanofluids as coolants extensively owing to their property of high thermal capacity,as compared to the classical heat transfer fluids. The potential benefits of using nanofluids over normal coolants include increased surface area of nanoparticles for heat exchange,reduction in pumping power due to the increased heat transfer,minimization in clogging,development of miniaturized systems resulting in savings in energy and capital.

The term “nanofluid” was christened by Choi and Eastman^[1]. The reason for the thermal con- ductivity and high heat transfer for these special fluid was studied by Buongiorno^[2] ,who proposed a comparatively satisfactory slip mechanism based on the model including the effects of Brownian motion and Thermophoresis of the nanoparticles suspended. His suggested mathematical model was later uti- lized and modified by Nield and Kuznetsov^{[3, 4]},Kuznetsov and Nield^{[5, 6]},Bhadauria et al.^[7] ,Agarwal and Bhadauria^[8] with the assumption that the value of the nanoparticle fraction at the boundary can be controlled as the temperature thereat. Since the porous medium is one of the key participants in many heat transfer situations,based on the same assumptions,studies were carried out by Bhadauria and Agarwal^{[9, 10]} and Agarwal and Bhadauria^[11] pertaining to rotating porous media saturated by a nanofluid. The problem of double diffusive convective transport where the base fluid is itself a solution, like salt solution,was examined by Kim et al.^[12] ,Kuznetsov and Nield^[13],Agarwal et al.^[14] ,and Yadav et al.^[15] . Binary nanofluids have wide applications as follows: (i) working fluids in absorption refrig- eration,i.e.,in absorption systems using water based Lithium Bromide and Ammonia solution with both magnetic and non-magnetic metal nanoparticles sufficiently enhance the heat transfer and also help in improving the mass transfer due to high rate of mixing; (ii) a medium for electro or electroless plating; (iii) transfer medium in medical treatments; (iv) geological processes such as crustal heat and solute transport,metamorphism,the diagenetic evolution of sedimentary basins and ore genesis; (v) geotechnical applications like underground disposal of nuclear wastes,liquid re-injection,contaminant transport in saturated soil,movement of moisture in fibrous insulation,and electro-chemical and drying processes.

These fields have initiated the utilization of nanofluids,which turn out to be binary nanofluids in the presence of other salts. Also these involve rotating porous media in the form of the Earth crust.

The above studies assumed that the nanoparticle concentration can be controlled manually at the boundaries which is a physical situation quite hard to achieve,resulting in the need to modify the boundary conditions assumed. In their very recent work,Nield and Kuznetsov^[3] considered a new set of boundary conditions where the nanoparticle volume fraction value adjusts automatically under the assumption of no nanoparticle flux at the surface. With such an assumption,the presence of oscillatory convection turns oblivious due to the absence of the two opposing agencies affecting instability. The study was further promoted by Agarwal^[16] and Agarwal et al.^[17] . In spite of this,we encounter the oscillatory convection in the present case due to the presence of solute particles under rotational effects.

In the present article,we study the Horton-Rogers-Lapwood problem for double diffusive convection in a rotating porous medium with revised boundary conditions,obeying Darcy’s Model.

2 Mathematical formulation

Assume an infinite stretch of binary nanofluid layer sandwiched in a rotating porous medium,with edges at z = 0 and z = d,heated from below and cooled from above. The edges permit free movement of heat and nanoparticle concentration. The nanofluid layer extends infinitely in x- and y-directions, with the z-direction extending vertically upward originating from the lower boundary. The porous layer rotates uniformly about the z-direction with the uniform angular velocity . The centrifugal force term is considered to be absorbed into the pressure term,while the momentum equation contains the Coriolis force term. T_h and T_c are the temperatures at the lower and upper walls,respectively, such that T_h > T_c. The resulting equations describing the flow problem are^{[2, 3]}

where v_D = (u,v,w) is the fluid velocity. Here,c_p is the specific heat (at the constant pressure),D_sm is the solutal diffusivity for the porous medium,and D_CT is a diffusivity of Soret type. Assuming the temperature and the solutal concentrations to be constant,and the nanoparticle flux to be zero at the edges,we get the boundary conditions as follows: The dimensionless variables are considered as where k_T = k_m/ (ρc_p)f ,and γ= (ρc_p)m/(ρc_p)f . Then,Eqs. (1)-(7) on non-dimensionalization take the following forms (after dropping the asterisk sign): Here,the non-dimensional numbers appearing follow their contemporary definitions.

3 Basic solution

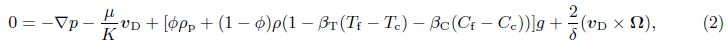
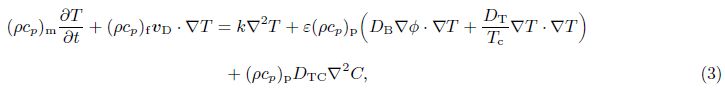
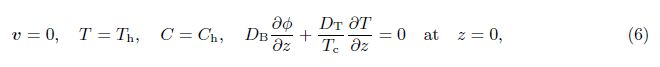
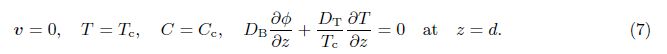
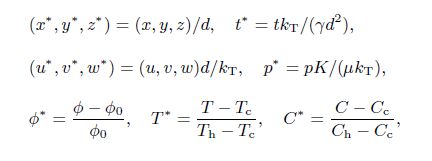
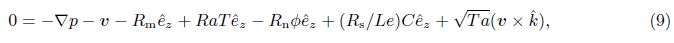
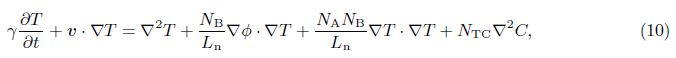
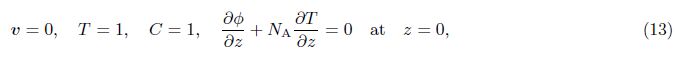
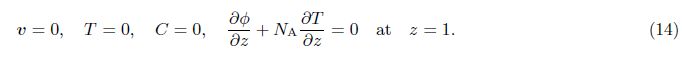
The quantities at the quiescent state vary only in the z-direction and will be given by

Substituting Eq. (15) into Eqs. (11)-(14),we get Under the boundary conditions (13) and (14),the integration of Eq. (18) can be obtained as Using this to solve Eqs. (16) and (17),we obtain Then,Eq. (19),now on integration,along with the boundary conditions assumed,leads to

4 Stability analysis

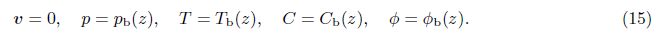
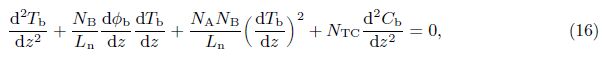
For small disturbances onto the quiescent state,i.e.,

assuming all physical quantities of the form (x,0,z) leading to the case of two dimensional rolls,we further substitute the above variables of Eq. (23) into Eqs. (9)-(12),and use the quiescent state results to obtain the following equations under linearity: − subject to the following boundary conditions:

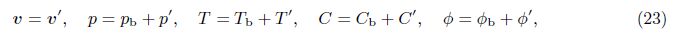
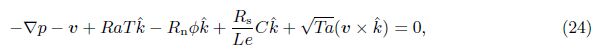
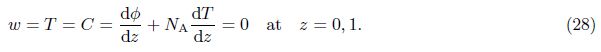
The parameter R_m is not carried over in the subsequent equations since it is part of the hydrostatic equilibrium. Operate the curl on Eq. (24) for its vertical component as

Re-operating the curl on Eq. (24),and writing the vertical component,we obtain where ζ = ∇ × v. The operator ∇²,is the contemporary two-dimensional Laplacian operator in the horizontal plane. Combining the above two equations yields To find the solution for the unknown fields in Eqs. (31) and (25)-(27),we use the normal mode technique, and thus obtain where l and m are the wave numbers in the x- and y-directions,respectively,and s = ζ¹ + iζ² is the growth rate. The system with ζ¹ < 0 is always stable,while it is unstable when ζ¹ > 0. For the neutral stability state,ζ¹ = 0. Hence,considering s = iζ² and rearranging the above equation yield The expressions for ℵ1 and ℵ₂ are not given here to save the space. R_a being a physical quantity needs to be real compulsorily. Hence,from Eq. (33) it follows that either ζ² = 0 (stationary/aperiodic onset) or ℵ₂ = 0 (ζ² ≠ 0,oscillatory/periodic onset). Substituting these expressions into the differential equations (31) and (25)-(27),we get where D = d/dz ,and α = (l² + m²)^1/2 is the non-dimensionalized horizontal wavenumber. We use the expressions below to approximate a solution of Eqs. (34)-(38) using the Galerkin-type method where satisfy the boundary condition (38). Putting the expressions of Eq. (39) into Eqs. (34)-(37),we obtain a system of 4N linear algebraic equations in the unknowns,namely,A_n,B_n,C_n,D_n,n = 1,2,· · · ,N. For a non-trivial solution for the equations in the system,equating the determinants of the coefficients of the linear equations to zero leads to a solution for R_a in terms of the other parameters.

5 Onset of instability 5.1 Stationary/aperiodic convection

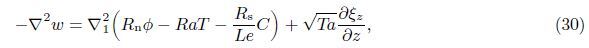
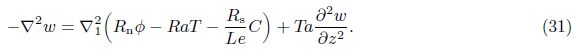
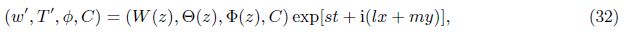
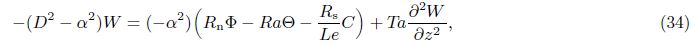
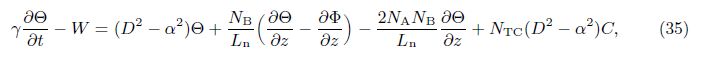
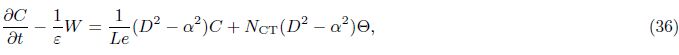
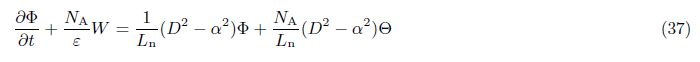
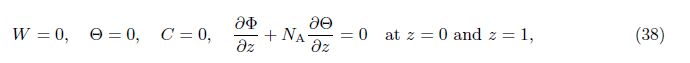
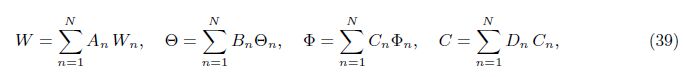
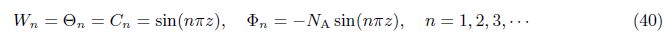
In the case of neutral stability,we take ζ¹ = 0 in our analysis. For the aperiodic convection ζ² = 0, we take N = 1 and get the value of Ra^st as

where δ2 = α2 + π2.

5.2 Oscillatory/periodic convection

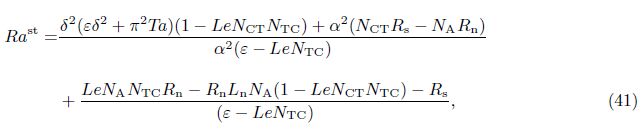
For the oscillatory onset ℵ₂ = 0 (ζ² ≠ 0) in Eq. (33),we can obtain

with the frequency of oscillations ζ² given by (on dropping the subscript 2) where

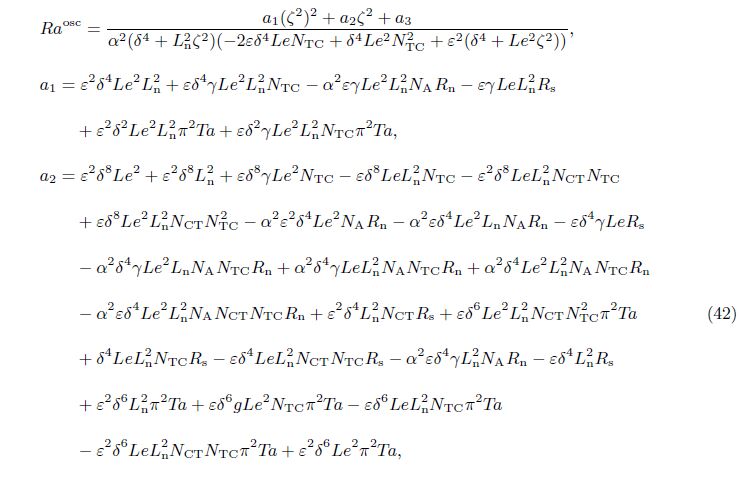
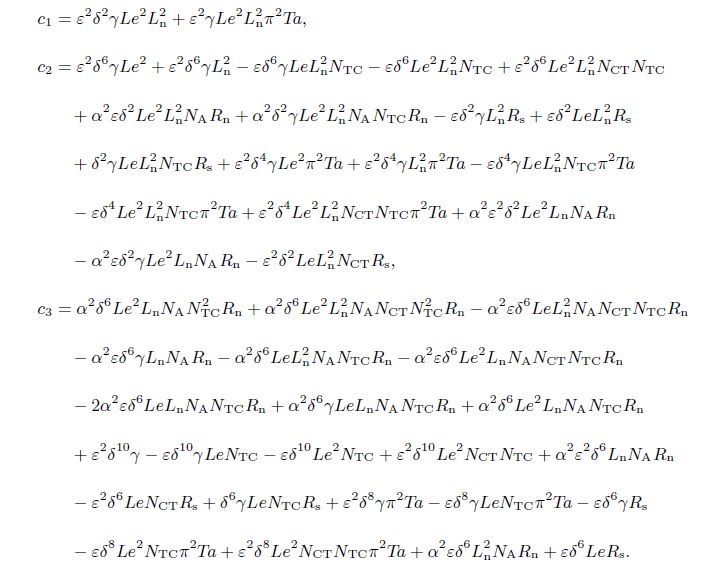
For the periodic convection to be achievable,ζ² needs to be positive and real,thus,c₂² − 4c₁c₃ > 0 while for ζ² < 0,though real valued,no periodic instability is possible.

6 Results and discussion

The thermal convection in a binary nanofluid saturated rotating porous layer in the linear case has been analyzed. The zero nanoparticle flux including thermophoretic effects is considered at the edges. T_hough with the current choice of boundary conditions the possibility of existence of overstability is negated under normal situations,it exists in the present case due to the presence of solute particles along with the nanoparticles. The analytic expressions for periodic and aperiodic modes of convection have been obtained as Eqs. (41) and (42),respectively. We shall discuss various limiting cases for this. When it is a non-rotating system,T_a = 0,which results in

Reducing the system of Eq. (41) from the triple component phase to the double component phase,the parameters

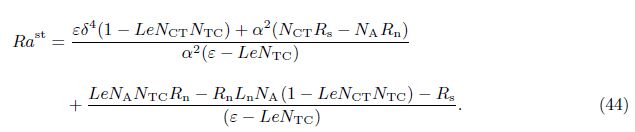
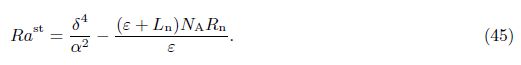
In the case of ordinary fluid,L_n = 0 =

which is in general true for double diffusive convection of an ordinary Newtonian fluid.

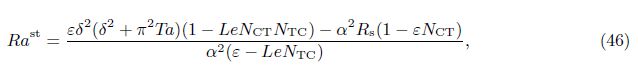
Now for a single component phase,we shall obtain from the above system as follows:

which coincides with the result of Vadasz. In the absence of rotation,as α varies,we acquire the following minimum value of R_ast at α = π: which is a result obtained by Nield and Kuznetsov^[3]. Hence,it is evident that,nanoparticles being absent,we shall get an already established value for the critical R_ayleigh-Darcy number of 4π2.

We can rearrange the above result as

to get the value of the sum of thermal R_ayleigh number R_a and the concentration R_ayleigh number R_n as 4π2,we get an alike result reported by Nield and Bejan^[18] on the classical double diffusive convection. Also it is worth considering that the application of a single term Galerkin approximation results to the same standard results without any overestimates. It is important to observe here that we get an upper bound of the value from the above expressions.

The nanoparticle flux does not contribute to the thermal energy conservation evident from the disappearance of the parameter N_B from the subsequent equations due to the orthogonality of the first-order trial functions and their first derivatives in the approximation theory employed.

Figure 1 deals with the comparative study of onset of convection between a binary nanofluid and a simple nanofluid,i.e,between two-phase state and a three-phase state. It is to be noticed that convection sets in earlier in the two-phase state than that in the triple-phase. T_his may be attributed to the presence of ordinary sized particles in the base fluid of a binary nanofluid along with the nano sized particles,which have a thermal conductivity lower than the nano particles. Because this convection gets delayed. According to Chandrashekhar^[19] and Drazin and Reid^[20],for the “Exchange of Stabilities” to hold good,oscillatory should be the mode of onset of convection which should transmit to the case of damped oscillations for a classical R_ayleigh-B´enard problem. The current problem follows the latter concept documented by Fig. 2,where convection sets in with oscillatory mode and finally grows aperiodically as damped oscillations.

In Figs. 3-11,we draw the neutral stability curves depicting the variation of thermal R_ayleigh number R_a with the wave number α. The results shown in Figs. 3-5 and Fig. 11 indicate that the concentration R_ayleigh number R_n,thermo-nanofluid Lewis number L_n,modified diffusivity ratio N_A and porosity of the medium ε have destabilizing effects on the system. A_n increase in the value of any of these parameters leads to the decrease in the value of critical thermal R_ayleigh number R_acr, indicating an advancement in the onset of convection. The effect of these graphically supports what can be concluded by looking at the expression of the thermal R_ayleigh number in Eq. (41). The proceeding figures,Figure 6-Figure 10 depict a stabilizing effect on the conformity of the remaining parameters,T_aylor’s number T_a,solutal-R_ayleigh number R_s,thermo-solutal Lewis number Le,Soret parameter N_CT and Dufour parameter N_TC. A_n increase in their values delays the onset of convection just as expected.

7 Conclusions

The problem of thermal instability in a binary nanofluid saturated a rotating porous medium has been studied analytically for the linear case. The porous layer is heated from below and cooled from above. The considered Darcy model includes the Brownian diffusion and thermophoresis effects. The expressions for the aperiodic and periodic convection are obtained analytically. Various limiting cases have been validated. The following conclusions are drawn graphically:

(i) The convection is delayed in binary nanofluids than ordinary nanofluids.

(ii) Oscillation is the preferred mode for onset of convection which transforms to the stationary mode at a later stage.

(iii) The parameters R_n,L_n,N_A,ε have a diminishing effect on the system,since they enhance the onset of convection. (iv) The parameters T_a,R_s,Le,N_CT,N_TC stabilize the system by leading to a delay in the onset of convection.