Article Information
- Haibo WANG, Ruirui LIU, Jialing YANG, Hua LIU, Yuxin SUN. 2016.
- Theoretical model for elliptical tube laterally impacted by two parallel rigid plates
- Appl. Math. Mech. -Engl. Ed., 37(2): 227-236
- http://dx.doi.org/10.1007/s10483-016-2027-8
Article History
- Received Jan. 6, 2015;
- in final form Jun. 29, 2015
2. Jiuquan Satellite Launch Centre, Jiuquan 732750, Gansu Province, China
| a, initial horizontal semi-axis; | E, elastic modulus of material; |
| λ, effective length of plastic hinge; | d, thickness of tube wall; |
| b, initial vertical semi-axis; | μ, Poisson’s ratio of material; |
| ρ, mass density of material; | l, breadth of tube wall; |
| R, initial radius of circular tube; | σ0, yield stress of material; |
| γ, linear density of material; | δ, displacement of plate; |
| h = b/a , ovality of elliptical tube; | EP, linear hardening modulus of material. |
The energy absorption or crashworthiness of materials and structures under impact is an important problem in engineering. Circular rings and tubes are one of the most commonly used structural elements due to their low cost and easy manufacturability. They can dissipate the input kinetic energy into the plastic energy and frictional work through different modes of deformation, resulting in different energy absorption responses. Deformation modes of short circular tubes include axial crushing, tube splitting, and tube inversion[1, 2, 3, 4, 5]. Since the deformation modes of tubes and rings are different, the energy absorption characteristics as well as the LOAd-displacement curves are different. As a result, they are used in different equipments, and relative investigations have been conducted by researchers[6, 7].
Circular rings are usually LOAded laterally. Zhang and Guo[8] theoretically analyzed the behavior of a circular ring between two rigid plates, with one of them subjected to the lateral impact. The model was based on the six-hinge mechanism presented by Burton and Craig[4], which was employed to study the quasi-static lateral compression of a circular tube between two parallel rigid plates. Since a quasi-static deformation mode is adopted, the system has only one degree-of-freedom, and it is easy to derive the deformation prOCess of the system. The calculation results indicate that the strain rate effect can improve the reaction force clearly at the initial stage of the motion, while the strain hardening effect and large deformation can affect the reaction force significantly at the final stage of the motion.
Compared with circular tubes, elliptical tubes have particular characteristics as energy absorbers on account of their different semi-axes. Vertical elliptical tubes can get longer stroke when laterally compressed, while horizontal elliptical tubes can get stable reaction forces. Morris et al.[9] and Olabi et al.[10] examined the quasi-static behavior of nested circular and elliptical type energy absorbers using experimental and numerical techniques. The LOAd-deflection curves were analyzed, and it was demonstrated that the elliptical tubes exhibit greater crush efficiency and more stable reaction force than the circular ones. They suggested that such energy absorbers may find applications where the structures are subjected to compressive impulsive LOAds, examples being crash barriers, aircraft fuselages, and oil tankers. Wu and Carney[11, 12] investigated the initial collapse behavior of braced elliptical tubes under the lateral compression through the theoretical analysis, experimental test, and finite element simulation. The ovality of the elliptical tubes varied from 0.5 to 2. They found that elliptical tubes provided a distinct advantage over their original circular tube counterparts.
By reviewing the existing literature, both the quasi-static and dynamic behavior of circular tube between two plates under the lateral compression has been investigated in detail. The elliptical tube under the quasi-static lateral compression was theoretically analyzed recently by Liu et al.[13]. However, no attempt has been made to investigate the dynamic behavior of elliptical tubes under the lateral compression theoretically. In this paper, we try to develop an analytical model to study the crushing behavior and energy absorption capability of a single elliptical tube, with and without considering the effect of strain hardening. The results will be compared with finite element results.
2 Plastic large deformation analysis for elliptical tube 2.1 Theoretical modelConsider an elliptical tube under the lateral impact by two parallel rigid plates, with the initial horizontal semi-axis a, the vertical semi-axis b, the ovality h = b/a, the width l, the thickness d, the volume density ρ, and the linear density γ, as shown in Fig. 1(a). Initially, two parallel rigid plates with the mass G strike on the top and bottom of the elliptical tube at the veLOCity v0. Then, the two plates move together with the elliptical tube. That is to say, the elliptical tube is subjected to the impulse I0 = Gv0 on the top and bottom surfaces, respectively, and in the opposite sense, four plastic hinges OCcur at points A, B, C, and D. The collapse mode of the elliptical tube is shown in Fig. 1(b), where δ is the displacement of the plate. The plastic deformation appears at the plastic hinges A, B, C, and D, while the arcs BA, BD, CD, and CA remain rigid during the impact prOCess. Different from the quasi-static compression problem, the active forces are the moments on the plastic hinges M1 and M2. Two coordinate systeMs are utilized to study the motion of the arc AC, as illustrated in Fig. 2. The fixed coordinate system Oxy is attached to the earth ground, and the moving coordinate system O1x0y0 is attached to the arc AC and moves together with it. Assume that the arc AC rotates in the anticLOCkwise direction by an angle θ. Then, the upper plate is in contact with the arc AC at the point V , with the vertical coordinate component in the fixed coordinate system of[13]
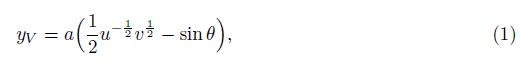

|
| Fig. 1 Collapse mechanism of elliptical tube impacted by two parallel rigid plates |
Fig. 2 Illustration of two coordinate systeMs for arc AC
The veLOCity and acceleration of the plate are $\dot y$V and y$\ddot V$ , respectively, and their expressions can be obtained from the time derivative and second time derivative of Eq. (1), respectively,
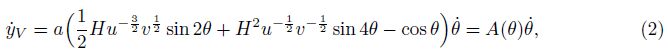

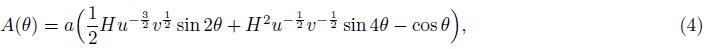
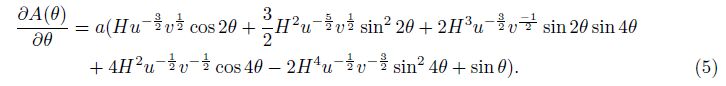
It is shown in Fig. 2 that the instantaneous center of zero veLOCity of the arc AC is the point p. For an arbitrary point K on the arc AC, the coordinate components in the coordinate system O1x0y0 attached to the arc are

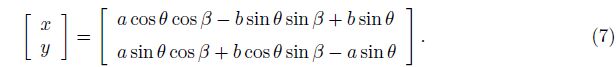
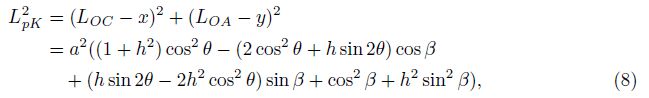
The differential length along the arc AC is ds = a . Then, the moment
of the inertia of the arc AC about the point p can be obtained as
. Then, the moment
of the inertia of the arc AC about the point p can be obtained as
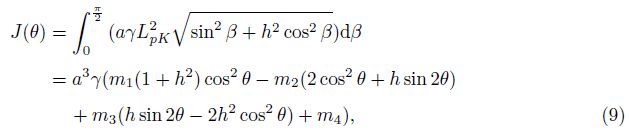
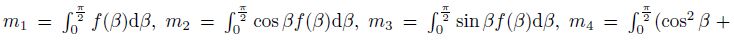
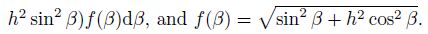
The system composed by the elliptical tube and the two rigid plates has one degree-offreedom, and the position of the system can be determined using the coordinate θ. The kinetic energy of the system is
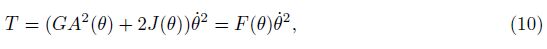

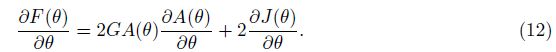

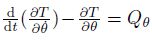 yields the differential equation of the problem as
yields the differential equation of the problem as
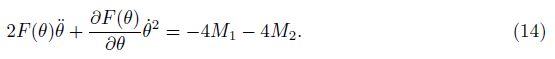
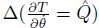 is the generalized momentum, and
is the generalized momentum, and 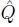 = 2aI0 is the generalized
impulse. It is known that θ0 = 0 when t = 0. Therefore, the initial kinetic energy of the system
T0 is
= 2aI0 is the generalized
impulse. It is known that θ0 = 0 when t = 0. Therefore, the initial kinetic energy of the system
T0 is
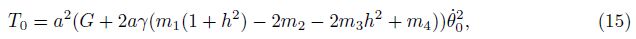
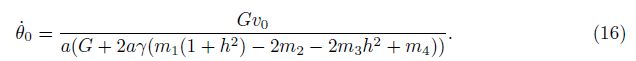
In the present model, the following assumptions are made: (1) The kinetic energy of the plate is much larger than the plastic limit strain energy of the elliptical tube; (2) A rigid-plastic idealization of the material is considered; (3) d/(2a) ≪ 1, the effects of the axial and shearing forces on the buckling are ignored.
Both the strain rate effect and strain hardening effect for the elliptical tube are considered to describe the deformation during the lateral impact period. The strain rate effect is described by Cowper-Symonds model, in which a rigid-perfectly plastic material model is adopted, and the relationship between the dynamic limit yielding stress σd and strain rate "˙ is described as

For linear hardening materials, the above relationship can be changed into

It can be obtained from Eqs. (17) and (18) that
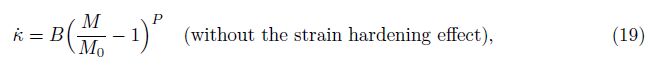
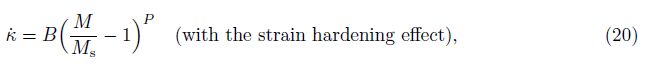
Assume that the effective length of the plastic hinge, λ, remains constant during the deformation of the elliptical tube, and let λ = id, where d is the thickness of the elliptical tube, and i is a constant coefficient. The relationship between the angular veLOCity θ and $\dot k$ is θ = λ$\dot k$ .
With the consideration of the linear strain hardening effect, the moment is
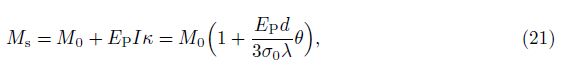
For the linear strain hardening rigid-plastic materials, the moments of the plastic hinges are
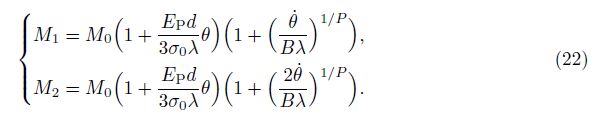
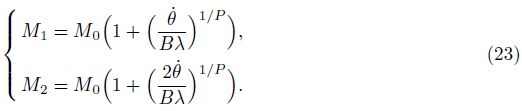
The relationship between the volume density ρ and the length density for the elliptical tube is given by

Now, the governing equation of this problem together with the initial conditions is derived as
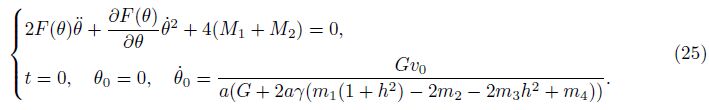

Finite element models in accordance with the theoretical analysis are constructed in order to verify the accuracy of the theoretical model. The explicit code LS-DYNA is employed.
The finite element model is shown in Fig. 3, which is composed of three parts: the upper plate, the elliptical tube, and the lower plate. The two plates are meshed using 3D rigid body elements with the vertical displacement component only, and the elliptical tube is meshed using the constant stress 3D solid element. The contact between the upper plate and the elliptical tube and that between the elliptical tube and the lower plate are both set as the ‘automatic surface to surface contact’ with the friction coefficient of 0.2, which can prevent the horizontal motion of the elliptical tube when it is compressed. The two plates have the same mass of G = 32.2 kg and are moving at the same initial veLOCity of v0 = 4.5 m/s. The material parameters of the elliptical tube are shown in Table 1.

|
| Fig. 3 Numerical model for finite element analysis |
Figure 4 compares the results predicted by the FEM and the analytical model without considering the strain hardening effect. The horizontal semi-axis a is 40 mm, the thickness d is 1.5 mm, and the width l is 5 mm. The force-displacement curve and the displacement-time curve of two cases related to the ovality h are shown, and the values of h are 1.4 and 1.6, respectively.

|
| Fig. 4 Comparison of numerical and theoretical results without considering strain hardening effect |
When an elastic body is subjected to an instantaneous impact LOAd, its displacement as well as the acceleration will vibrate. Since the rigid plate moves together with the elliptical tube after it strikes on the tube, the reaction force is proportional to the acceleration, as shown in Eq. (26). As a result, the reaction force will vibrate. In numerical simulation of the FEM, the elasticplastic material model is adopted. Because elastic behavior is considered, the reaction force exerted on the plate vibrates at the initial deformation stage of the elliptical tube, as shown in Figs. 4(a) and 4(c). In addition, since the strain hardening effect is ignored, the reaction force exerted on the plate increases slowly and even has a tendency of dropping down when the elliptical tube fully enters the plastic stage. When the deformation of the elliptical tube is large enough, the reaction force on the plate continues to increase. In the theoretical analysis, the constant length of the plastic hinge is adopted as λ = 1.5d. Therefore, the numerical results of the reaction force-displacement curve is in good agreement with the analytical results when δ/a < 0.88. However, the numerical result increases faster than the theoretical result when δ/a > 0.88. It is shown in Figs. 4(b) and 4(d) that the displacement-time curves obtained from the two methods are in good agreement.
3.3 Calculation results with considering strain hardening effectFigure 5 shows the comparison of the results from the FEM and analytical results with the strain hardening effect considered. The parameters of the elliptical tube are the same as those used in Subsection 3.2 excEPt that the linear hardening modulus is EP = 4 500 MPa. Similar to Fig. 4, excellent agreement between the results from the FEM and analytical results of the displacement-time curve is obtained, as shown in Figs. 5(b) and 5(d). In the theoretical analysis, the constant length of the plastic hinge is adopted as λ = 7d. The numerical results of the reaction-displacement curve are in good agreement with analytical results when δ/a < 0.88. However, the numerical result increases faster than that of the theoretical prediction when δ/a > 0.88. It should be noted that the reaction force exerted on the plate continues to increase when the strain hardening effect is considered. This is different from the case without considering the strain hardening effect.

|
| Fig. 5 Comparison of numerical and theoretical results when EP = 4 500 MPa |
The four-hinge collapse mode is used in the theoretical analysis of dynamic behavior of elliptical tube impacted by two parallel rigid plates, and the strain rate effect as well as the strain hardening effect is considered. The system is simplified to one degree-of-freedom, and the governing equations are derived from Lagrange equations of the second kind. The dynamic response of the elliptical tube is obtained. The analytical results are compared with the numerical results of finite element analysis. It is shown that the dynamic responses of the system are different with and without considering the strain hardening effect when the elliptical tube fully enters the plastic stage. The reaction force exerted on the plate increases slowly and even has a tendency of dropping down if the strain hardening effect is ignored, while it continues to increase when the strain hardening effect is considered.
| [1] | Kinkead, A. N. Analysis for inversion load and energy absorption of a circular tube. Journal of Strain Analysis, 18(3), 177-188(1983) |
| [2] | Yang, J. L., Luo, M., Hua, Y. L., and Lu, G. X. Energy absorption of expansion tubes using a conical-cylindrical die: experiments and numerical simulation. International Journal of Mechanic Sciences, 52(5), 716-725(2010) |
| [3] | Deruntz, J. A. and Hodge, P. G. Crushing of a tube between rigid plates. Journal of Applied Mechanics, 30, 391-395(1963) |
| [4] | Burton, R. H. and Craig, J. M. An investigation into the energy absorbing properties of metal tubes loaded in the transverse direction, B. Sc. dissertation, University of Bristol, England (1963) |
| [5] | Huang, X., Lu, G., and Yu, T. X. On the axial splitting and curling of circular metal tubes. International Journal of Mechanical Sciences, 44(11), 2369-2391(2002) |
| [6] | Yu, T. X. and Lu, G. X. Energy Absorption of Structures and Materials (in Chinese), Chemical Industry Press, Beijing (2006) |
| [7] | Olabi, A. G., Morris, E., and Hashmi, M. S. J. Metallic tube type energy absorbers: a synopsis. Thin-Walled Structures, 45, 706-726(2007) |
| [8] | Zhang, T. G. and Guo, X. G. The large viscoplastic deformation of a ring subjected to lateral impulsive loading (in Chinese). Explosion and Shock Waves, 10(1), 55-61(1990) |
| [9] | Morris, E., Olabi, A. G., and Hashmi, M. S. J. Lateral crushing of circular and non-circular tube systems under quasi-static conditions. Journal of Materials Processing Technology, 191(1-3), 132-135(2007) |
| [10] | Olabi, A. G., Morris, E., and Hashmi, M. S. J. Optimised design of nested oblong tube energy absorbers under lateral impact loading. International Journal of Impact Engineering, 35(1), 10-26(2008) |
| [11] | Wu, L. and Carney, J. F., III. Initial collapse of braced elliptical tubes under lateral compression. International Journal of Mechanical Sciences, 39(9), 1023-1036(1997) |
| [12] | Wu, L. and Carney, J. F., III. Experimental analyses of collapse behaviors of braced elliptical tubes under lateral compression. International Journal of Mechanical Sciences, 40(8), 761-777(1998) |
| [13] | Liu, R. R., Wang, H. B., Yang, J. L., Liu, H., and Sun, Y. X. Theoretical analysis on the quasi-static lateral compression of elliptical tube between two rigid plates. Applied Mathematics and Mechanics (English Edition), 36, 1005-1016(2015) DOI 10.1007/s10483-015-1962-7 |
 2016, Vol. 37
2016, Vol. 37



