1 Introduction

Carbon nanotubes (CNTs) are allotropes of carbon with a cylindrical nanostructure. Nanotubes have been constructed with the length-to-diameter ratio, which is up to 132 000 000:1^[1], much larger than that for any other materials. These cylindrical carbon molecules have unusual properties, which are valuable for nanotechnology, electronics, optics, and other fields of materials science and technology. In particular, owing to their extraordinary thermal conductivity and mechanical and electrical properties, CNTs can be used as additives to various structural materials. For instance, nanotubes form a tiny portion of the material in some (primarily carbon fiber) baseball bats, golf clubs, or car parts^[2]. Nanotubes are members of the fullerene structural family. Their name is derived from their long and hollow structure with the walls formed by one-atom-thick sheets of carbon, called graphene. These sheets are rolled at specific and discrete (“chiral”) angles, and the combination of the rolling angle and radius decides the nanotube properties, for example, whether the individual nanotube shell is a metal or semiconductor. Nanotubes are categorized as single-walled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs).

Sometimes, the classical theory cannot describe some phenomena of the material at the atomic level. The classical (local) theory assumes that the stress at a defined point depends uniquely on the strain at the same point. But there are theories that are capable for considering small scale effects such as Eringen, couple stress, modified couple stress theory (MCST), and strain gradient. The MCST has been used by many researchers in order to analyze sizedependent structures. For instance, Simsek and Reddy^[3] investigated the bending and vibration of functionally graded (FG) micro beams using a new higher order beam theory and the MCST. Wang et al.^[4] presented the size-dependent vibration analysis of three-dimensional cylindrical micro beams based on the MCST.

In present, mechanical behavior of beams is studied by applying various beam theories. It should be noted that the Euler-Bernoulli beam theory (EBT) is only applicable for slender beams, and the shear deformation effect is not considered. The Timoshenko beam theory (TBT) accounts for the shear deformation effect for short beams by assuming a constant shear strain through the height of the beam. To avoid the use of shear correction factor, higher order shear deformation theories were developed based on the assumption of the higher order variation of axial displacement through the height of the beam such as the sinusoidal shear deformation beam theory (SSDBT)^[5]. Yoon et al.^[6] carried out the vibration and instability of CNTs conveying fluid. Kiani^[7] studied the effects of the small-scale parameter, inclination angle, speed, and density of the fluid flow on the maximum dynamic amplitude factors of longitudinal and transverse displacements. Based on the nonlocal TBT, the buckling analysis of an SWCNT embedded in an elastic medium was reported by Murmu and Pradhan^[8]. Results show the dependency of critical dynamic load on the nonlocal parameter and surrounding medium. Applying the nonlocal elasticity field theory in nanomechanics and an exact variational principal approach, Lim^[9] derived the new equilibrium conditions, domain governing differential equations, and boundary conditions for bending of nanobeams. Mirramezani et al.^[10] showed that based on their result, they could have developed an innovative model for one dimensional coupled vibrations of CNTs conveying fluid using the slip velocity of the fluid flow on the CNT walls as well as utilizing size-dependent continuum theories to consider the size effects of nanoflow and nano-structure. Kaviani and Mirdamadi^[11] showed that considering the small-size effects of the flow field on the dynamic characteristics of CNTs conveying the fluid is essential. They investigated the wave propagation analysis of CNTs conveying the fluid including the slip boundary condition and the strain/inertial gradient theory. Ghorbanpour Arani et al.^[12] carried out the surface effects on the frequency analysis of nanotubes using the nonlocal TBT. Gheshlaghi and Hasheminejad^[13] investigated the surface effects on the nonlinear free vibration of nanobeams. Malekzadeh and Shojaee^[14] presented the surface and nonlocal effects on the nonlinear free vibration of non-uniform nanobeams. They found that the increase of the amplitude ratio causes the reduction of the surface effects. The longitudinal free vibration analysis of axially FG microbars was investigated by Akg$\ddot o$z and Civalek^[15] on the basis of strain gradient elasticity theory. They utilized the Rayleigh-Ritz solution technique to obtain an approximate solution to the free longitudinal vibration problem of strain gradient microbars for clamped-clamped and clamped-free boundary conditions. In another work by Akg$\ddot o$z and Civalek^[16], buckling behavior of size-dependent microbeams made of functionally graded materials (FGMs) for different boundary conditions was investigated on the basis of EBT and modified strain gradient theory. Based on the nonlocal continuum theory, Wang et al.^[17] investigated the nonlinear vibration of an embedded SWCNT subjected to a harmonic load. Xu and Deng^[18] established variational principles for the buckling and vibration of MWCNTs with the aid of the semi-inverse method. The size-dependent stability behavior of nano-sandwich plates was investigated by Ghorbanpour Arani et al.^[19] using the MCST. Akg$\ddot o$z and Civalek^[20] performed the thermo-mechanical size-dependent buckling analysis of embedded FG microbeams based on the SSDBT and the MCST. The effects of the thickness-to-material length scale parameter ratio, material property gradient index, slenderness ratio, temperature change, and Winkler parameter on critical buckling loads of embedded FG microbeams were discussed in detail.

Based on the best knowledge of the authors, the dynamic instability of SWCNTs has not been reported based on the SSDBT. In the present work, the dynamic stability of the SWCNTs subjected to the harmonic load is investigated based on the SSDBT. The size effects are considered using the MCST. The SWCNTs are embedded in a realistic visco-Pasternak medium. Motion equations of system are derived using the energy method and Hamilton’s principle. The differential quadrature method (DQM) in conjunction with the Bolotin method is applied for obtaining the dynamic instability region (DIR) of the SWCNTs. The effects of the nonlocal parameter, visco-Pasternak foundation, mode numbers, and geometrical parameters on the DIR of SWCNTs are discussed in details.

2 Basic equations

A schematic figure for the SWCNT embedded in a visco-Pasternak foundation is shown in Fig. 1, where the geometrical parameters of the length (L), the thickness (h), and the radius (R) are also indicated.

2.1 SSDBT

The displacement fields of SWCNTs based on the SSDBT can be described as^[3]

in which where h is the beam thickness, u and w are the axial and the transverse displacements of any point on the neutral axis, respectively, t denotes the time, ' and  are the transverse shear strain of any point on the neutral axis and the total bending rotation of the cross-sections at any point on the neutral axis, respectively, and Φ(z) is a function of z, which characterizes the transverse shear stress distribution along the thickness of the beam.

2.2 MCST

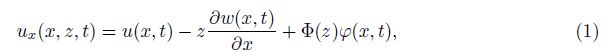
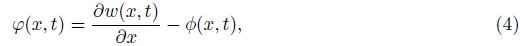
By considering the MCST, the strain energy density is related to the strain tensor and the curvature tensor. Thus, the strain energy of the bulk U_s in a deformed isotropic linear elastic material occupying the region Ω is given as follows^[4]:

where ε_ij and X_ij represent the strain and the symmetric rotation gradient tensors, respectively, which are defined by where u_i and e_ijk are the displacement vector and the alternate tensor, respectively. The classical stress tensor σ_ij and the higher order stress mij are given by where δij is the Kronecker product, $\bar E$ and $\bar G$ are the Lame constants, and l2 is the independent material length scale parameter. It is recalled that $\bar E$ = Eυ/(1+υ)(1−2υ), and $\bar G$ = $\bar E$/2(1+υ), where $\bar E$ and υ are Young’s modulus and Poisson’s ratio, respectively.

3 Energy method

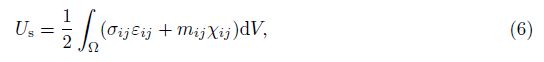
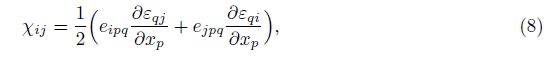
Substitution Eqs. (1)-(3) into Eq. (7), the strains are

where

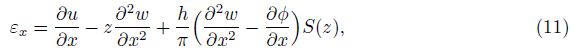
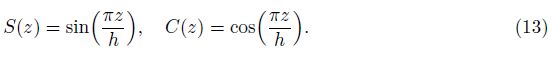
Substituting Eqs. (11) and (12) into Eq. (8) gives the symmetric rotation gradient tensors as 

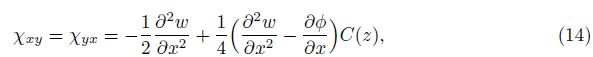
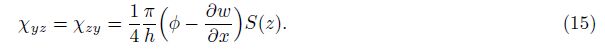
By using the above relations, the stresses and higher order stresses are

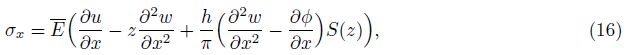
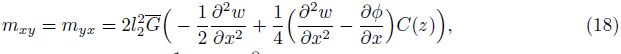
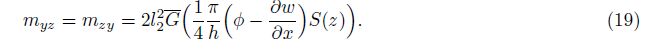
Substituting Eqs. (16)-(19) into Eq. (6) leads to

where

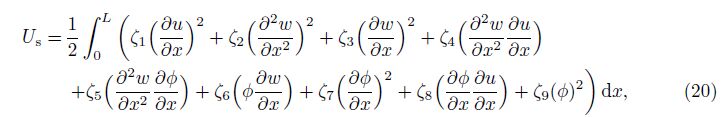
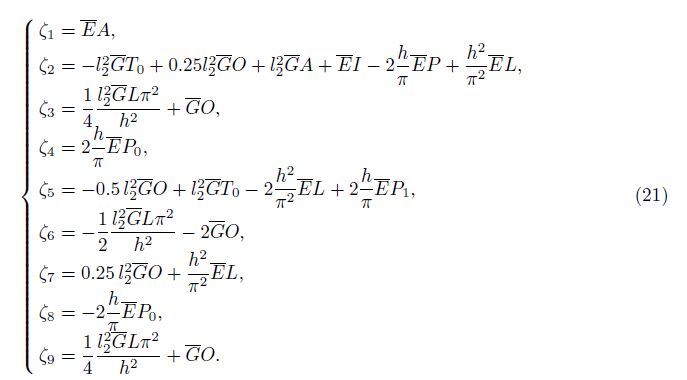
The following integrals are defined by

where

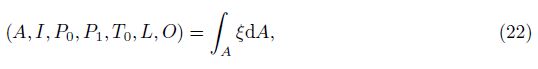
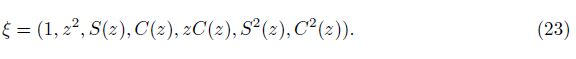
The total kinetic energy of nanotubes can be expressed as

where ρ_t is the density of nanotube. The external work due to a visco-Pasternak foundation is written as where K_w, C_d, and G_P are Winkler’s spring modulus, damper, and Pasternak’s shear modulus of an elastic medium, respectively.

3.1 Hamilton’s principle

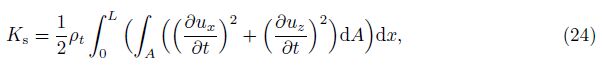
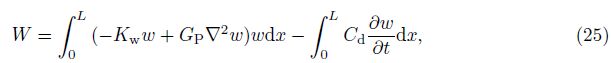
Hamilton’s principle is used to derive the motion equations of system as follows:

Integrating Eq. (26) by parts and setting the coefficients of δu, δw, and δ to zero lead to the following motion equations:

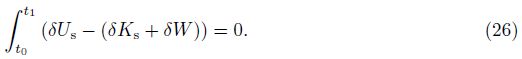
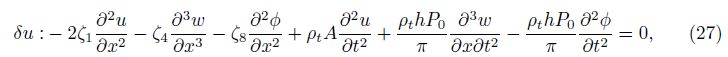
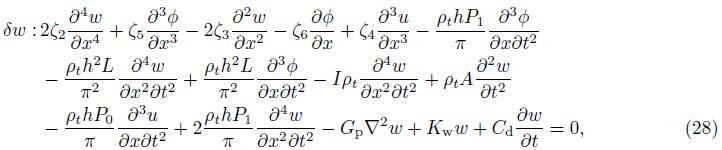
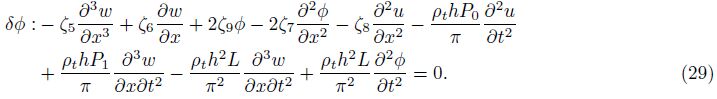
Furthermore, the boundary conditions at x = 0 and x = L can be obtained as

4 Solution procedure 4.1 DQM

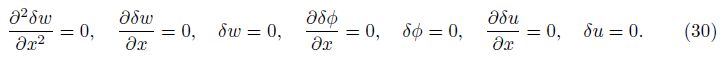
The DQM is employed in this section which in essence approximates the partial derivative of a function, with respect to a spatial variable at a given discrete point, as a weighted linear sum of the function values at all discrete points chosen in the solution domain of the spatial variable. Let F be a function representing u1, u2, w1, w2, 1, and 2, with respect to the variable x, in the domain of (0 < x < L) having Nx grid points along these variables. The nth-order partial derivative of F(x) with respect to x may be expressed discretely as

where A_ik⁽ⁿ⁾ is the weighting coefficient, whose recursive formula was described in Ref. ^[8]. The Chebyshev-Gauss-Lobatto polynomial^[8] is used to determine the unequally spaced position of the grid points as follows:

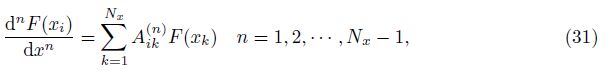
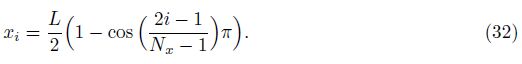
Combining all the motion equations along with the corresponding boundary conditions, using the DQM, and rewriting them in the matrix form yield

where M, C, and K are the mass, damping, and stiffness matrices, respectively, K_G is the geometrical stiffness matrix, d is the displacement vector (i.e., d = [u, v, w]), and in which ω is the frequency of excitation, Pcr is the static buckling load, α and α may be defined as static and dynamic load factors, respectively.

4.2 Bolotin method

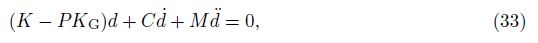
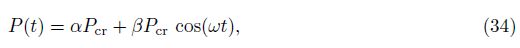
In order to determine the DIR of SWCNTs, the method suggested by Bolotin^[21] is applied. Hence, the component of d can be written in the Fourier series with the period 2T as

where ak and bk are undetermined constants according to this method.

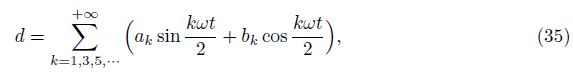
According to this method, The first instability region is usually the most important in studies of structures. It is due to the fact that the first DIR is wider than other DIRs, and the structural damping in higher regions becomes neutralized^[22]. Substituting Eq. (35) into Eq. (33) and setting the coefficients of each sine and cosine as well as the sum of the constant terms to zero, yield

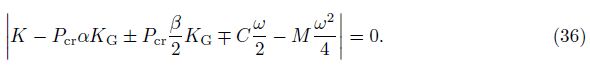
Solving the above equation based on the eigenvalue problem, the variation of ω with respect to α can be plotted as the DIR.

5 Results and discussion

In this approach, the effects of nonlocal parameter, visco-Pasternak foundation, mode numbers, and geometrical parameters on the DIR of SWCNTs are investigated. The material properties of the SWCNTs related to bulk are as follows: Young’s modulus E = 1 TPa, Poisson’s ratio  = 0.27, the density ρ = 2 300 kg/m³, the radius R = 0.5 nm, and the thickness h = 0.34 nm^{[17, 23]}.

To demonstrate the efficiency and accuracy of the present solution, the results are compared with the existing data available in literature. By neglecting the harmonic load and elastic foundation, the nonlocal natural frequency of a microbeam is obtained based on the SSDBT and the MCST. Considering the material properties, which are the same as those in Ref. ^[24] and the dimensionless frequency as , the results of validation are shown in Table 1 for different mode numbers and slenderness ratios based on the EBT, the TBT, and the SSDBT for both classical theory (CT) and MCST. It is evident that the results of the present work are in good agreement with those of Ref. ^[24], indicating the validity of the present study. It is also concluded that the difference between the present theory with the EBT and the TBT is significant for higher modes and smaller L/h. Therefore, the present beam should be used to predict the responses of shorter beams and higher modes where the shear deformation effect is significant.

Figure 2 illustrates the effect of various surrounding foundation on the dimensionless pulsation frequency. Four different elastic media are considered, namely, the visco-Pasternak (i.e., K_w = 1 × 10¹⁷, G_p=4, C_d=10), the Pasternak (i.e., K_w=1 × 10¹⁷, G_p=4, C_d = 0), the visco- Winkler (i.e., K_w=1×10¹⁷, G_p=0, C_d=10), and the Winkler (i.e., K_w=1×10¹⁷, G_p=0, C_d = 0) media. It is understood that the elastic foundation increases the dimensionless pulsation frequency, and the DIR shifts to the right. It is due to the fact that putting the SWCNT in an elastic medium makes the system more stable and stiffer. It is also concluded that the DIR of the Pasternak or visco-Pasternak model is higher than that of Winkler or visco-Winkler one. It is because the Pasternak model considers not only the normal stresses but also the transverse shear deformation and continuity among the spring elements. Furthermore, the DIRs predicted by the visco-Pasternak and visco-Winkler media are lower than those predicted by the Pasternak and Winkler models, respectively.

Figure 3 shows the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude for different mode numbers. Increasing the mode numbers, the dimensionless pulsation frequency and the DIR will increase.

Figure 4 depicts the effect of the ratio of length to thickness on the dimensionless pulsation frequency with respect to the dimensionless pulsation amplitude. It is obvious that increasing length to thickness ratio causes the DIR and dimensionless pulsation frequency to shift to the left and decrease, respectively. This is due to the fact that decreasing length to thickness ratio makes the system more stable.

Figure 5 demonstrates variations of the dimensionless pulsation frequency versus the dimensionless pulsation amplitude for different values of nonlocal parameters. It can be observed that the increment of nonlocal parameter in the MCST makes the DIR and dimensionless pulsation frequency shift to the right and increase. This is because the MCST expresses the one additional rotation gradient tensor.

6 Conclusion

The dynamic response of SWCNTs has applications in designing many NEMS/MEMS devices such as sensors, actuators, fluid storage, and solar cell. The dynamic stability of SWCNTs is studied in this paper. The size effects are considered based on the MCST. With the application of the SSDBT and Hamilton’s principle, the motion equations are derived. The DIR of the SWCNT is obtained using the DQM in conjunction with the Bolotin method. The effects of nonlocal parameter, visco-Pasternak foundation, mode numbers, and aspect ratio are shown in the dynamic response of system. Results indicate that the MCST is higher than the classical one. In addition, considering the elastic medium causes the DIR and dimensionless pulsation frequency to shift to right and increase. Furthermore, increasing length to thickness ratio causes the DIR and dimensionless pulsation frequency to shift to the left and decrease, respectively.