Article Information
- M. AREFI. 2016.
- Surface effect and non-local elasticity in wave propagation of functionally graded piezoelectric nano-rod excited to applied voltage
- Appl. Math. Mech. -Engl. Ed., 37(3): 289-302
- http://dx.doi.org/10.1007/s10483-016-2039-6
Article History
- Received Jun. 16, 2015;
- in final form Aug. 29, 2015
| u, v, w, displacement components; | lm, ls, non-local parameters; |
| x1, x2, x3, Cartesian coordinates; | φ, electric potential; |
| Tij , stress components; | V0, applied voltage; |
| εij , strain components; | b, h, dimensions of rod; |
| Bi, body force components; | ταβ, surface stress; |
| ai, acceleration components; | τ0, residual surface tension; |
| ρ, density; | μ0, λ0, surface Lame’s constants; |
| μ, λ, Lame’s constants; | U, total energies; |
| E, modulus of elasticity; | Us, surface energies; |
| υ, Poisson’s ratio; | Eek, kinetic energy; |
| Ek, electric field; | Di, electric displacement; |
| eijk, piezoelectric constants; | c, phase velocity; |
| ∇2, Laplacian operator; | k, wave number. |
Many theories have been proposed to consider a continuum environment. The classical models assumed that materials are continuous and the size of the constituted submaterials has no effect on the mechanical behaviors of the materials. Recently, numerous researchers have focused on the structures with very small size. They used new continuum mechanical models accounting size dependency. A non-local model based on Eringen’s theory of non-local continuum mechanics has been proposed for the effects of the size dependency in very small structures[1]. The results show that the effects of surface elasticity and residual stress are very important in the analysis of thin film and nano-scale structures. This condition becomes important when the thickness of the structure reduces to nano-scale[2, 3].
This paper tries to present the wave propagation solution for a functionally graded piezoelectric nano-rod by use of the non-local model excited by a two-dimensional (2D) electric potential. A literature review can present the necessity of this research. Hsu[4] studied the electromechanical behavior of piezoelectric laminated composite beams by use of the differential quadrature method (DQM). The Chebyshev-Gauss-Lobatto sample point equation was used to select the sample points, and the electromechanical responses of the piezoelectric laminated composite beams with various boundary conditions were determined. Lu et al.[5] used a non-local plate model for the Kirchhoff and the Mindlin plate models. The assumed theories were based on Eringen’s theory of non-local continuum. Wang et al.[6] employed the non-local elasticity solution for the evaluation of the length-dependent in-plane stiffness of achiral and chiral single-walled carbon nano-tubes. The length-dependent stiffness was revealed from the non-local elasticity. Song et al.[7] investigated the wave propagating in one-dimensional (1D) nano-structures with the initial axial stress. They used a non-local elastic model to incorporate with the strain gradient theory. The governing equations for the longitudinal and transverse waves in the bars and beams were derived by use of two scale parameters for introducing the size effect. The phase and group velocities of the wave propagation were obtained analytically. Ru[8] presented the linearized Gurtin-Murdoch model of surface elasticity. The proposed derivation offered a simple explanation for all unique features of the model and its simplified/modified versions.
Ke et al.[9] studied the non-linear free vibration of the functionally graded nano-composite beams reinforced by the single-walled carbon nano-tubes (SWCNTs) based on the Timoshenko beam theory and von K´arm´an geometric non-linearity. The Ritz method was employed to derive the governing eigenvalue equation. The effects of different parameters such as the nanotube volume fraction, the vibration amplitude, and the slenderness ratio were evaluated on the non-linear free vibration characteristics of the beams. S¸im¸sek[10] performed a non-linear dynamic analysis of a Flattened-Gaussian (FG) beam with a power law distribution due to a moving harmonic load by use of the Timoshenko beam theory. The fundamental equations were derived by use of the Lagrange equations. The effects of some parameters such as the material distribution and the speed of load were evaluated. Lu et al.[11] employed the Gurtin-Murdoch continuum surface elasticity model to study the buckling delamination of the ultra thin film-substrate system. The effects of the surface deformation and residual stress on the large deflection of the ultra thin film were considered.
Ke et al.[12] employed the non-local theory for the non-linear vibration of the piezoelectric Timoshenko nano-beam. The beam was subjected to an applied voltage and a uniform temperature change. The effects of various parameters such as the non-local parameter, the temperature change, and the external electric voltage were studied on the size-dependent nonlinear vibration characteristics of the piezoelectric nano-beam.
Ghorbanpour Arani et al.[13] analyzed the vibration of the coupled system of double-layered graphene sheets (CS-DLGSs). They assumed that the structure was embedded in a visco-Pasternak foundation, and employed the non-local elasticity theory of orthotropic plate. Ghorbanpour Arani et al.[14] studied the electro-thermal transverse vibration of fluid-conveying double-walled boron nitride nano-tubes (DWBNNTs). The elastic medium was described by spring and van der Waals (vdW) forces between the inner nano-tube and the outer nano-tube.
Rahimi et al.[15] presented an electroelastic analysis of a cylindrical shell by use of the energy method and the first-order shear deformation theory. Wu and Hui[16] evaluated the analytical and numerical solutions of a non-local elastic bar in the tension. Yan and Jiang[17] studied the effect of the surface elasticity on the vibration and buckling behavior of a simply supported piezoelectric nano-plate (PNP) by use of a modified Kirchhoff plate model. Two kinds of in-plane constraints were defined for the PNP, and the surface effects were accounted in the modified plate theory through the surface piezoelectricity model and the generalized Young-Laplace equations. Hadi et al.[18] studied the stresses and strains of a functionally graded Timoshenko beam subjected to an arbitrary transverse loading by the energy method. Nami and Janghorban[19] developed a new higher order shear deformation theory based on the trigonometric shear deformation theory for considering the size effects with the non-local elasticity theory. Hosseini-Hashemi et al.[20] considered the surface effects on the free vibration analysis of the Euler-Bernoulli and Timoshenko nano-beams by use of the non-local elasticity theory. The problem was solved for different types of boundary conditions. G$\ddot u$ven[21] presented the one-dimensional propagation wave in a nano-bar. The local and non-local solutions were evaluated for the wave velocity. Some electromechanical analyses of the functionally graded piezoelectric materials were performed[22, 23, 24, 25, 26, 27, 28, 29]. Ghorbanpour Arani and Jafari[30] employed the DGM to derive the equations of non-local and non-linear vibrations of the embedded laminated microplates resting on an orthotropic Pasternak medium. Non-linearity was considered by use of the von Karman relation. The effects of different parameters such as the non-local parameters, the elastic media, the aspect ratios, and the boundary conditions were considered on the non-linear vibration of the micro-plate.
Zenkour and Abouelregal[31] investigated a vibration analysis of a nano-beam made of the functionally graded material with the exponential distribution law by use of the non-local generalized thermoelasticity theory. Zare et al.[32] studied the natural frequencies of a functionally graded nano-plate for different combinations of boundary conditions. The material properties were considered to be variable along the thickness direction based on the power function. The effects of different boundary conditions were considered on the natural frequencies of the system.
The purpose of this study is to derive the fundamental governing differential equations of wave propagation in a functionally graded piezoelectric nano-rod excited by 2D electric potential and applied voltage at the top of the rod. For constituting the governing differential equations of the system, the unified non-local elasticity model and theory for the surface elasticity are used. The effects of some important parameters such as the material gradation and the applied voltage are considered on the characteristics of the wave propagation.
2 FormulationBased on the Love rod model, the displacement field is presented as follows[21]:
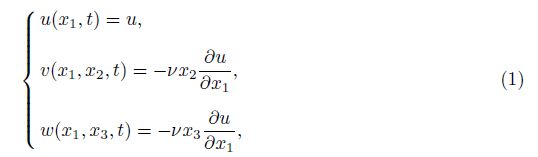
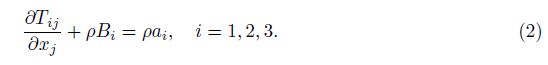
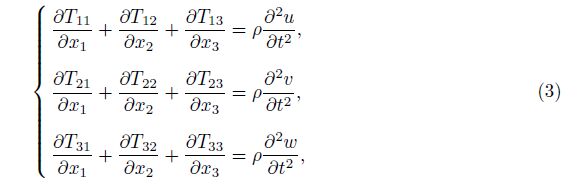
Referring to the assumed displacement field in Eq. (1), we can derive the strain components as follows:
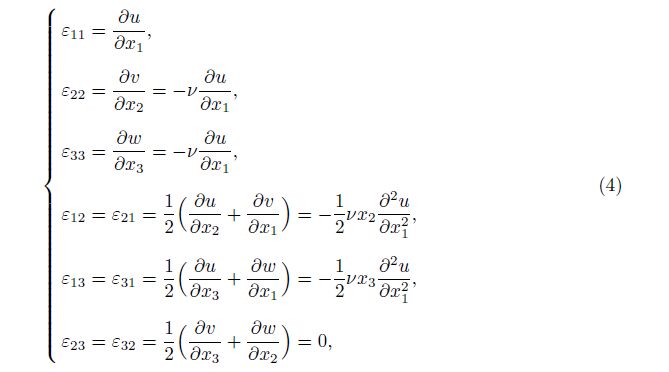
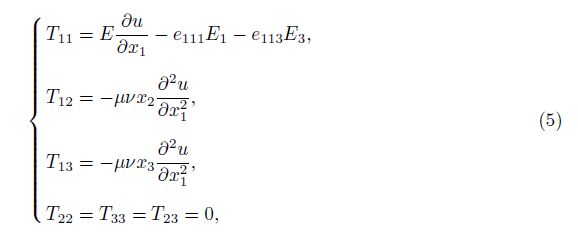
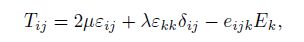
Substituting the non-zero components of the stress into the motion equations yields
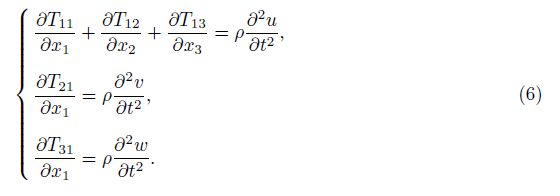
The unified non-local elasticity model is[1, 13, 21]
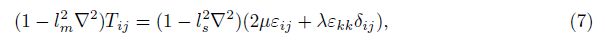
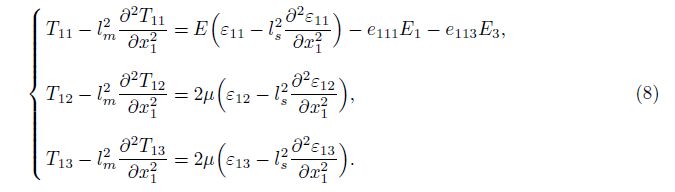
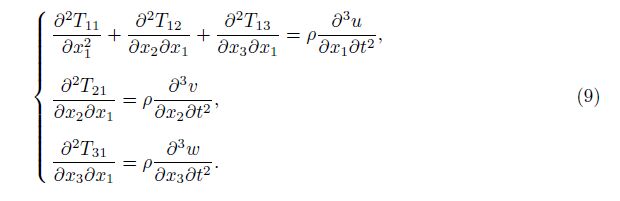
Substitute the shear stress in the first line of Eq. (9) from Eq. (6) in terms of the displacement components. Then, Eq. (9) can be rewritten as follows:
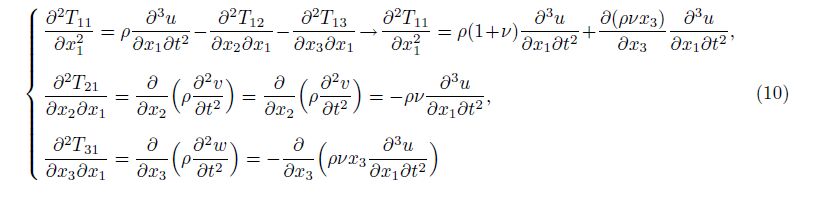
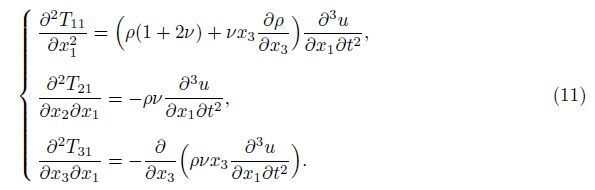
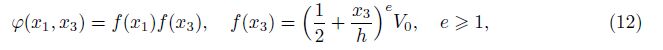
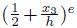 is the assumed distribution
for the electric potential along the transverse direction. For example, e = 1 corresponds to a
linear distribution electric potential, and e > 1 presents a higher order distribution electric
potential. For the above electric potential defined by Eq. (12), we have the electric field as
follows[22, 23]:
is the assumed distribution
for the electric potential along the transverse direction. For example, e = 1 corresponds to a
linear distribution electric potential, and e > 1 presents a higher order distribution electric
potential. For the above electric potential defined by Eq. (12), we have the electric field as
follows[22, 23]:
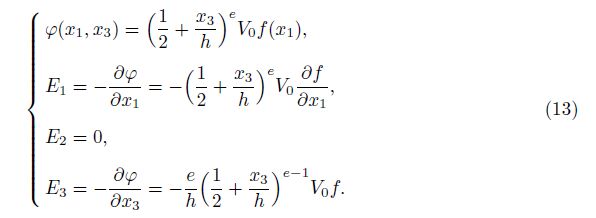
For more simplification in the derivation of equations, f(x1) is replaced with f. By considering the electric field components derived in Eq. (13), we can derive the three components of the stress as follows:
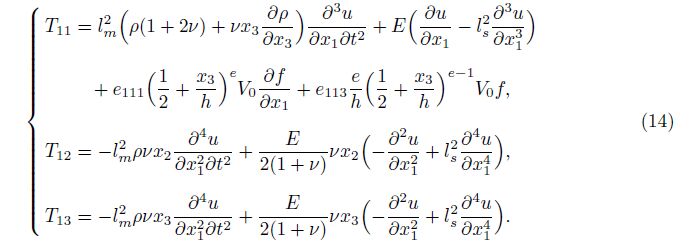
For an electromechanical system, the electric displacement is defined by[22, 23]
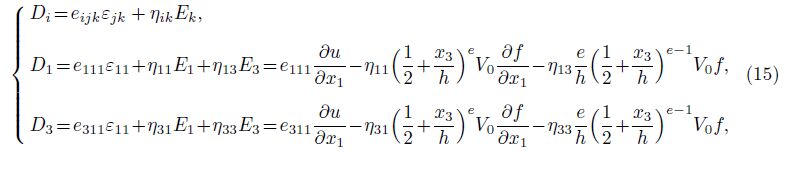
For a symbolic material property Ξ(x3), we have
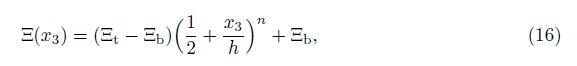
As we know, in sub-structures, the surface properties differ from the bulk properties. Due to this difference, the surface elasticity is used by introducing the surface stress as follows[11]:
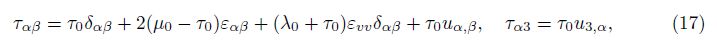
Then, we can evaluate the energy corresponding to the surface stress, i.e.,
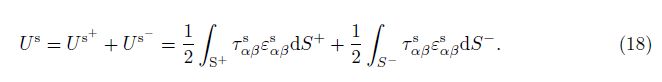
The obtained surface energy can be presented as follows:
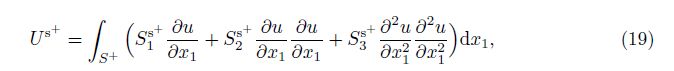
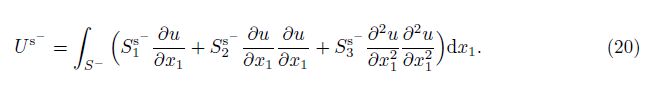
The kinetic energy of the system is evaluated as follows:
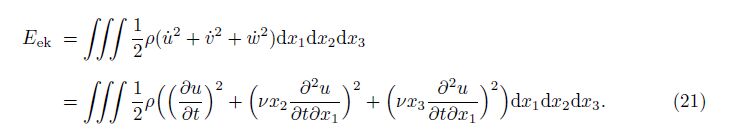
The strain energy of the system including the mechanical and electrical energies is introduced as follows[15]:
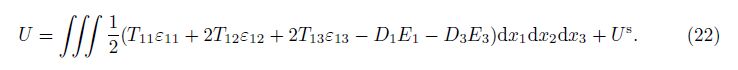
Substituting the corresponding equations for the stress, the strain, the electric displacement, and the electric field from Eqs. (1), (13), (14), and (15) yields the potential energy as follows:
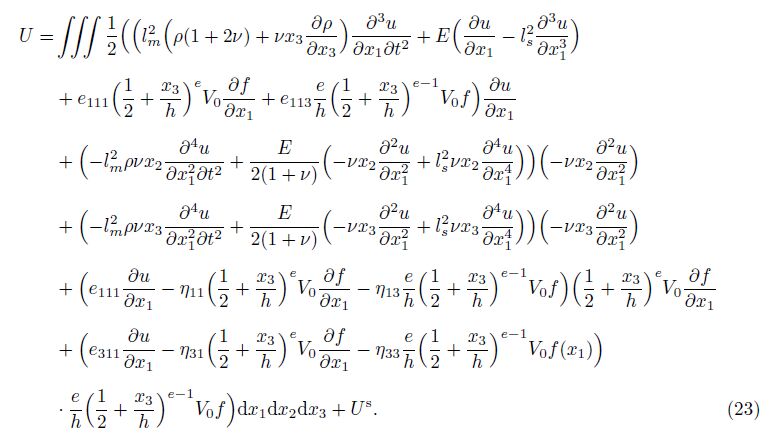
In order to evaluate the final differential equation of the system, the Hamilton principle is used. This principle implies that

Considering both the kinetic energy and the potential energy in the Hamilton principle and performing the integration by part operations yield two final differential equations as follows:
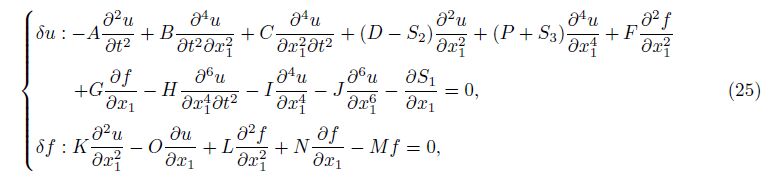
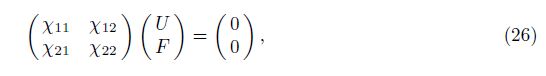

This section presents the numerical results of the problem in terms of different parameters of the electromechanical system. The obtained results contain the real and imaginary parts of the phase velocity c.
Figure 1 shows the distribution of the real part of the phase velocity c in terms of the wave number for different values of the non-homogeneous index when V0 = 10. When the wave number increases, the real part decreases considerably. Furthermore, it can be observed that when the non-homogeneous index increases, the real part of the phase velocity decreases considerably. This is due to the decrease in the stiffness of the structure along the axial direction.

|
| Fig. 1 Real part of c in terms of wave number for different values of nonhomogeneous index when V0 = 10 |
Figure 2 shows the distribution of the imaginary part of the phase velocity c in terms of the wave number for different values of the non-homogeneous index when V0 = 10.

|
| Fig. 2 Imaginary part of c in terms of wave number for different values of nonhomogeneous index when V0 = 10 |
The investigation on the effects of the used parameters indicates that when the wave number increases, the imaginary part tends to an asymptotic value. Furthermore, when the nonhomogeneous index increases, the imaginary part of the phase velocity increases. It can be concluded that for large values of the wave number, the values of the non-homogeneous index have no considerable effect on the imaginary part of the phase velocity.
3.1 Comparison between cases with and without surface effectThis section presents the numerical results considering the surface effect. For this consideration, the phase velocity is valuated in terms of different values of the wave number for two cases, i.e., with and without the surface effect. Figure 3 shows the distribution of the real part of the phase velocity c in terms of the wave number when V0 = 100. It can be concluded that when the wave number increases, the difference between the results increases considerably.

|
| Fig. 3 Comparison between real part of c in terms of wave number with and without surface effect when V0 = 100 |
Figure 4 shows the distribution of the real part of the phase velocity c in terms of the wave number when V0 = 10. The same conclusion presented for Fig. 3 can be found. It can be concluded from Figs. 3 and 4 that the surface elasticity in the derivation of the relations decreases the phase velocity of the nano-rod, especially for large values of the wave number.

|
| Fig. 4 Comparison between real part of c in terms of wave number with and without surface effect when V0 = 10 |
In order to study the effect of the applied voltage on the phase velocity, the obtained results are evaluated for different values of the applied voltage. Figures. 5 and 6 show the distributions of the imaginary and real parts of the phase velocity in terms of different values of the wave number for different values of the applied voltage, respectively.

|
| Fig. 5 Imaginary part of c in terms of wave number for different applied voltages |

|
| Fig. 6 Real part of c in terms of wave number for different non-homogeneous indexes |
The obtained results indicate that when the applied voltage increases, the imaginary part decreases considerably. The investigation on the obtained results in Fig. 6 indicates that the applied voltage has no considerable effect on the real part of the phase velocity.
3.3 Effect of non-local parametersIn this section, the effects of the non-local parameter are considered on the results of the problem. Figures. 7 and 8 show the real and imaginary parts of the phase velocity in terms of the non-local parameter ls or lm, where ls = lm.

|
| Fig. 7 Real part of c in terms of non-local parameter ls (lm) |

|
| Fig. 8 Imaginary part of c in terms of non-local parameter ls (lm) |
The obtained results in Figs. 7 and 8 indicate that when the non-local parameter increases, both the real and imaginary parts of c decrease. This behavior agrees with the obtained results in Ref. [14].
4 ConclusionsIn this study, the non-local elasticity solution and the surface elasticity effect are developed for the analysis of the wave propagation in a functionally graded piezoelectric nano-rod excited by a 2D electric potential and an applied voltage at the top of the rod. The effects of different important parameters such as the surface effect, the applied voltage, the non-local parameter, and the non-homogeneous index are investigated on the real and imaginary parts of the phase velocity. Some important results are expressed as follows:
(i) The wave number plays an important role in the real and imaginary parts of the phase velocity. The real part decreases considerably while the imaginary part tends to an asymptotic value when the wave number increases.
(ii) The obtained results with and without the surface effect show that the difference between the two considered cases increases considerably when the wave number increases, and the phase velocity with the surface effect is smaller than that without the surface effect.
(iii) When the applied voltage increases, the imaginary part decreases considerably while the real part changes little.
(iv) The non-local parameter used in the non-local elasticity solution has a decreasing trend on the phase velocity of the nano-rod when the non-local parameter increases.
Appendix A
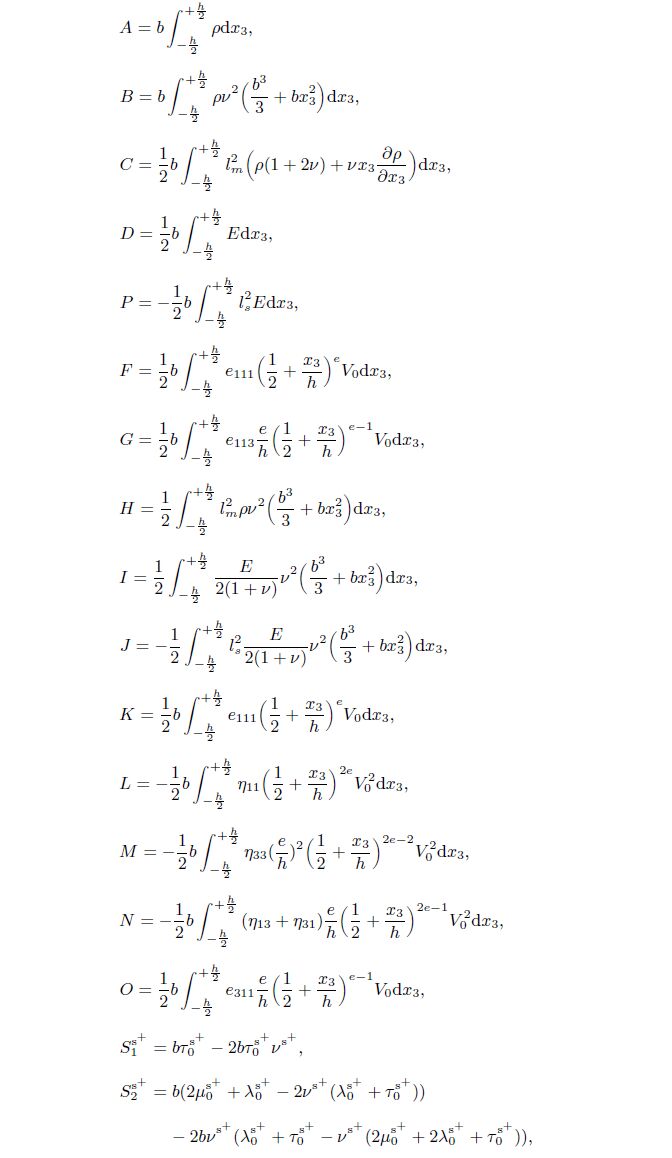
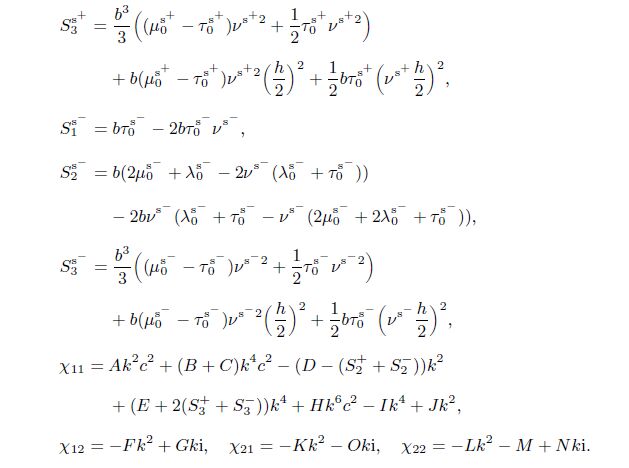
| [1] | Eringen, A. C. On differential equations of non-local elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54, 4703-4710 (1983) |
| [2] | Gurtin, M. E. and Murdoch, A. A. Continuum theory of elastic material surfaces. Archive for Rational Mechanics and Analysis, 57, 291-323 (1975) |
| [3] | Gurtin, M. E. and Murdoch, A. Surface stress in solids. International Journal of Solids and Structures, 14, 431-440 (1978) |
| [4] | Hsu, M. H. Electromechanical analysis of piezoelectric laminated composite beams. Journal of Marine Science and Technology, 13, 148-155 (2005) |
| [5] | Lu, B. P., Zhang, P. Q., Lee, H. P., Wang, C. M., and Reddy, J. N. Non-local elastic plate theories. Proceedings of the Royal Society A, 463, 3225-3240 (2007) |
| [6] | Wang, Q., Han, Q. K., and Wen, B. C. Estimate of material property of carbon nano-tubes via non-local elasticity. Advances in Theoretical and Applied Mechanics, 1, 1-10 (2008) |
| [7] | Song, J., Shen, J., and Li, X. F. Effects of initial axial stress on waves propagating in carbon nano-tubes using a generalized non-local model. Computational Materials Science, 49, 518-523 (2010) |
| [8] | Ru, C. Q. Simple geometrical explanation of Gurtin-Murdoch model of surface elasticity with clarification of its related versions. Science China: Physics, Mechanics and Astronomy, 53, 536- 544 (2010) |
| [9] | Ke, L. L., Yang, J., and Kitipornchai, S. Non-linear free vibration of functionally graded carbon nano-tube-reinforced composite beams. Composite Structures, 92, 676-683 (2010) |
| [10] | Şimşek, M. Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Composite Structures, 92, 2532-2546 (2010) |
| [11] | Lu, T. Q., Zhang, W. X., and Wang, T. J. The surface effect on the strain energy release rate of buckling delamination in thin film-substrate systems. International Journal of Engineering Science, 49, 967-975 (2011) |
| [12] | Ke, L. L., Wang, Y. S., and Wang, Z. D. Non-linear vibration of the piezoelectric nano-beams based on the non-local theory. Composite Structures, 94, 2038-2047 (2012) |
| [13] | Ghorbanpour Arani, A., Shiravand, A., Rahi, M., and Kolahchi, R. Non-local vibration of coupled DLGS systems embedded on visco-Pasternak foundation. Physica B, 407, 4123-4131 (2012) |
| [14] | Ghorbanpour Arani, A., Shokravi, M., Amir, S., and Mozdianfard, M. R. Non-local electrothermal transverse vibration of embedded fluid-conveying DWBNNTs. Journal of Mechanical Science and Technology, 26, 1455-1462 (2012) |
| [15] | Rahimi, G. H., Arefi, M., and Khoshgoftar, M. J. Electro elastic analysis of a pressurized thickwalled functionally graded piezoelectric cylinder using the first order shear deformation theory and energy method. Mechanika, 18, 292-300 (2012) |
| [16] | Wu, Z. X. and Hui, D. H. Solution for a non-local elastic bar in tension. Science China: Physics, Mechanics and Astronomy, 55, 1059-1065 (2012) |
| [17] | Yan, B. Z. and Jiang, L. Y. Vibration and buckling analysis of a piezoelectric nano-plate considering surface effects and in-plane constraints. Proceedings of the Royal Society A, 468, 3458-3475 (2012) |
| [18] | Hadi, A., Daneshmehr, A. R. N., Mehrian, S. M., Hosseini, M., and Ehsani, F. Elastic analysis of functionally graded Timoshenko beam subjected to transverse loading. Technical Journal of Engineering and Applied Sciences, 3, 1246-1254 (2013) |
| [19] | Nami, M. R. and Janghorban, M. Static analysis of rectangular nano-plates using trigonometric shear deformation theory based on non-local elasticity theory. Beilstein Journal of Nanotechnology, 4, 968-973 (2013) |
| [20] | Hosseini-Hashemi, S., Fakher, M., and Nazemnezhad, R. Surface effects on free vibration analysis of nano-beams using non-local elasticity: a comparison between Euler-Bernoulli and Timoshenko. Journal of Solid Mechanics, 5, 290-304 (2013) |
| [21] | Güven, U. A generalized non-local elasticity solution for the propagation of longitudinal stress waves in bars. European Journal of Mechanics, A/Solids, 45, 75-79 (2014) |
| [22] | Khoshgoftar, M. J., Arani, A. G., and Arefi, M. Thermoelastic analysis of a thick walled cylinder made of functionally graded piezoelectric material. Smart Materials and Structures, 18, 115007 (2009) |
| [23] | Arefi, M. and Rahimi, G. H. Application of shear deformation theory for two dimensional electroelastic analysis of an FGP cylinder. Smart Structures and Systems, 13, 1-24 (2014) |
| [24] | Arefi, M. and Khoshgoftar, M. J. Comprehensive piezo-thermo-elastic analysis of a thick hollow spherical shell. Smart Structures and Systems, 14, 225-246 (2014) |
| [25] | Arefi, M. and Nsahas, I. Non-linear electro thermo elastic analysis of a thick spherical functionally graded piezoelectric shell. Composite Structures, 118, 510-518 (2014) |
| [26] | Arefi, M. Non-linear thermoelastic analysis of thick-walled functionally graded piezoelectric cylinder. Acta Mechanica, 224, 2771-2783 (2013) |
| [27] | Rahimi, G. H., Arefi, M., and Khoshgoftar, M. J. Application and analysis of functionally graded piezoelectrical rotating cylinder as mechanical sensor subjected to pressure and thermal loads. Applied Mathematics and Mechanics (English Edition), 32, 997-1008 (2011) DOI 10.1007/s10483- 011-1475-6 |
| [28] | Arefi, M. and Rahimi, G. H. Comprehensive thermoelastic analysis of a functionally graded cylinder with different boundary conditions under internal pressure using first-order shear deformation theory. Mechanika, 18, 5-13 (2012) |
| [29] | Arefi, M., Rahimi, G. H., and Khoshgoftar, M. J. Exact solution of a thick walled functionally graded piezoelectric cylinder under mechanical, thermal and electrical loads in the magnetic field. Smart Structures and Systems, 9, 427-439 (2012) |
| [30] | Ghorbanpour Arani, A. and Jafari, G. S. Non-linear vibration analysis of laminated composite Mindlin micro/nano-plates resting on orthotropic Pasternak medium using DQM. Applied Mathematics and Mechanics (English Edition), 36, 1033-1044 (2015) DOI 10.1007/s10483-015-1969-7 |
| [31] | Zenkour, A. M. and Abouelregal, A. E. Thermoelastic interaction in functionally graded nanobeams subjected to time-dependent heat flux. Composite Structures, 18, 909-924 (2015) |
| [32] | Zare, M., Nazemnezhad, R., and Hashemi, H. S. Natural frequency analysis of functionally graded rectangular nano-plates with different boundary conditions via an analytical method. Meccanica, 50, 2391-2408 (2015) |
 2016, Vol. 37
2016, Vol. 37


