Article Information
- S. ASAD, A. ALSAEDI, T. HAYAT. 2016.
- Flow of couple stress fluid with variable thermal conductivity
- Appl. Math. Mech. -Engl. Ed., 37(3): 315-324
- http://dx.doi.org/10.1007/s10483-016-2031-6
Article History
- Received May 29, 2015;
- in final form Sept. 11, 2015
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
Nowadays, many researchers in scientific and engineering fields have shown great interest in non-Newtonian fluids since non-Newtonian fluids play a vital role in industrial processes. The theory for the mechanics of non-Newtonian fluids is necessary due to the insufficiency of Newtonian fluids in predicting the behaviors of many fluids, particularly the fluids with high molecular weight[1, 2, 3, 4, 5]. The boundary layer flow of a non-Newtonian fluid on a moving surface is an important type of flows arising in many technological processes. Akg$\ddot u$l and Pakdemirli[6] studied the unsteady squeezed flow of a power-law fluid over a porous surface. Jalil et al.[7] investigated the analytical solutions for a non-linear problem arising in the boundary layer flow of a power-law fluid over a power-law stretching surface, and observed that the boundary layer thickness and the skin friction coefficient increased when the non-linear parameter decreased. Mishra et al.[8] considered the effects of heat and mass transfer on the free convective boundary layer flow of a viscoelastic fluid, and considered an electrically conducting fluid past a vertical porous plate in the presence of a heat source. Rashad et al.[9] analyzed the effect of the transpiration velocity on the free convection flow of a non-Newtonian fluid over a cone. Sahoo[10] addressed the partial slip effects and heat transfer in the von Karman flow of the Reiner-Rivlin fluid. Zheng et al.[11] examined the boundary layer flow of a pseudo-plastic fluid over a moving surface. Turkyilmazoglu[12] explored the mixed convection flow of a magnetohydrodynamic (MHD) viscoelastic fluid over a stretching surface. Awais et al.[13] discussed the Newtonian heating effects in the steady flow of a thixotropic fluid. Hayat et al.[14, 15] examined the unsteady three-dimensional and stagnation point flow of a couple stress fluid with chemical reactions and melting heat transfer, respectively. Nadeem et al.[16] studied the boundary layer flow of a second-grade fluid due to a moving cylinder with heat transfer.
The aforementioned investigations show that, little has been reported yet to the boundary layer flow of a non-Newtonian fluid by a stretching cylinder with heat transfer. Such attempts for variable thermal conductivity of a fluid have not been presented. There are liquid metals, for which the thermal conductivity varies with the temperature in the range from 0F to 400F[17, 18]. Motivated by such a fact, we aim here to examine the flow of a couple stress fluid by a stretching cylinder. The thermal conductivity is taken to be temperature dependent. The couple stress fluid is assumed to allow the polar effects such as the effects of couple stresses, body couple, and non-symmetric tensors. These effects make the present fluid distinct from other non-Newtonian fluid models. The mathematical problems are formulated and the solutions to the non-linear analysis are computed by a modern technique known as the homotopy analysis method (HAM)[19, 20, 21, 22, 23, 24]. The results are discussed via plots for different parameters.
2 Mathematical formulationWe consider the steady flow of an incompressible couple stress fluid. The flow is generated due to an inclined cylinder. The stretching cylinder makes an angle α with the vertical axis. The velocity component x and r are normal to each other. Thermal radiation effects are taken into account. The thermal conductivity of the fluid is taken to be temperature dependent. The boundary layer equations comprising the conservation laws of mass, linear momentum, and energy can be written as follows:

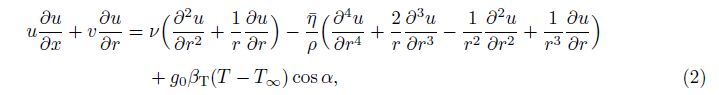
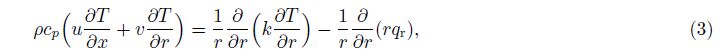
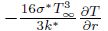 is the radiative heat flux, in which k* is the mean absorption
coefficient. g0 is the acceleration due to gravity. βT is the volumetric coefficient of thermal
expansion. σ* is the Stefan-Boltzmann constant. k is the variable thermal conductivity of the
fluid defined by
is the radiative heat flux, in which k* is the mean absorption
coefficient. g0 is the acceleration due to gravity. βT is the volumetric coefficient of thermal
expansion. σ* is the Stefan-Boltzmann constant. k is the variable thermal conductivity of the
fluid defined by

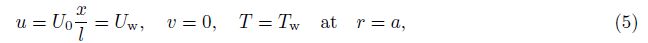
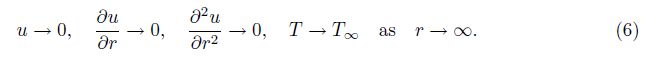
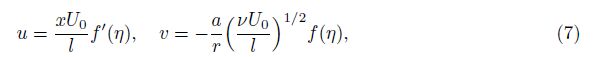
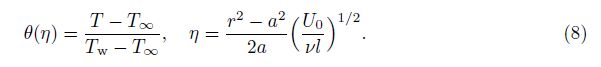
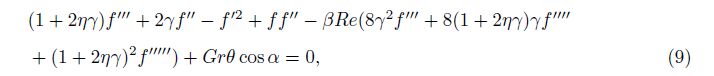
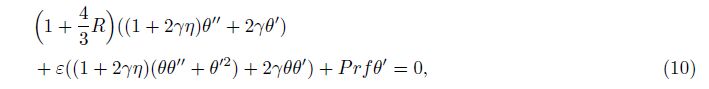

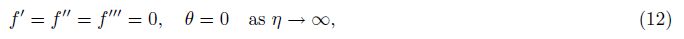
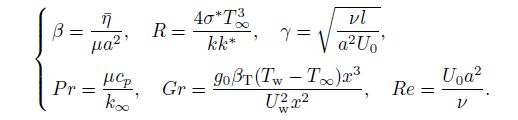
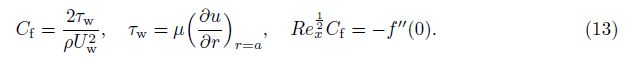
The initial guesses and auxiliary linear operators for the velocity and temperature fields are
The zeroth-order deformation problems can be represented as follows:
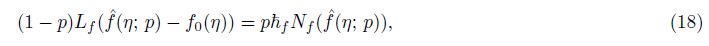
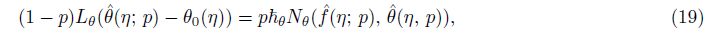
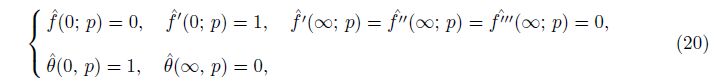
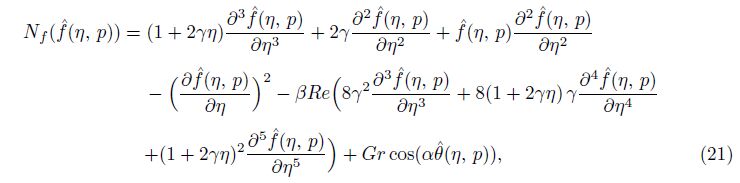
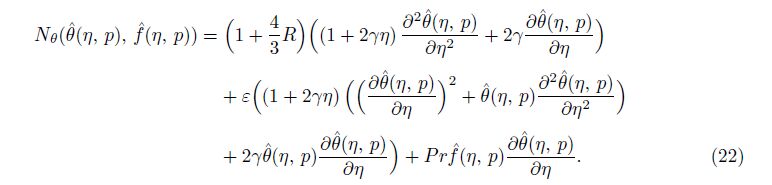
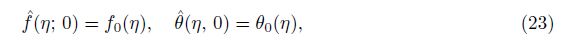
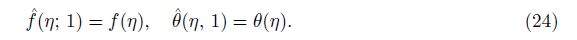
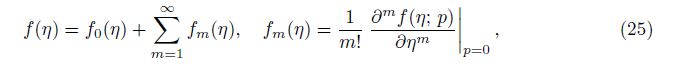
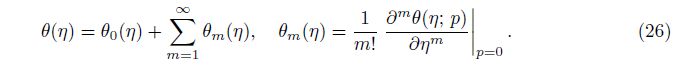


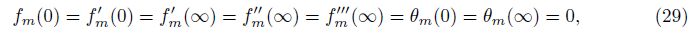
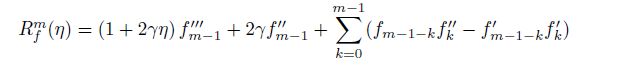
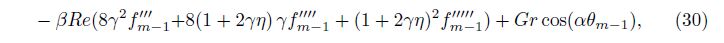
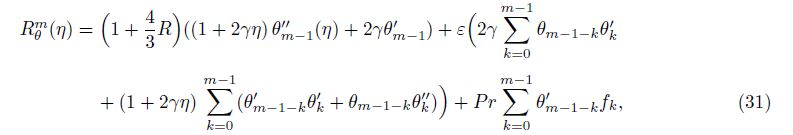

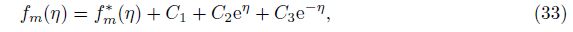
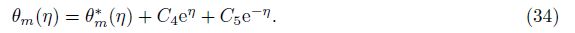
The convergence of the series solutions depends upon the non-zero auxiliary parameter ħ. To find the convergence region of the series (27) and (28), we plot the ħ-curves for the velocity and temperature profiles (see Fig. 1). Figures 1(a) and 1(b) witness that the admissible values of ħf and ħθ are -1.5≤ħf≤-0.3 and -1.4≤ħθ≤-0.4, respectively. These series solutions converge for the whole region of η when ħf = -0.9 and ħθ = -0.75.

|
| Fig. 1 ħ-curves for velocity field and temperature field |
Table 1 depicts the convergence of the series solutions. It is confirmed here that the 20thorder approximations are enough for the convergence of the velocity and temperature profiles.
 |
The results about the effects of the couple stress parameter β, the Reynolds number Re, the Prandtl number Pr, the variable thermal conductivity parameter ε, the radiation parameter R, and the curvature parameter γ are shown in Figs. 2-12. Figures 2-6 show the effects of β, Re, γ , Gr, and α on the velocity field, respectively, while Figs. 7-12 present the effects of β, Re, γ ε, R, and Pr on the temperature field, respectively.
From Figs. 2 and 3, we can see that the velocity decreases when β and Re increase. This is due to the fact that the couple stress parameter depends upon the couple stress viscosity η, and this couple stress viscosity acts as a retarding agent, which makes the fluid denser. Meanwhile, clearly, the Reynolds number is the ratio of the inertia force to the viscous force. Therefore, when the Reynolds number increases, the actual inertial force plays the dominant role in comparison with the viscosity. Therefore, for larger Reynolds numbers, the velocity decreases to zero when η increases, and the flow decays very slowly to the ambient.

|
| Fig. 2 Effects of β on velocity field |

|
| Fig. 3 Effects of Re on velocity field |
From Fig. 4, we can see that the variation of γ near the cylinder wall is negligible when y≤1, and the velocity increases when η > 1. This is due to the fact that the curvature parameter is inversely proportional to the radius of the cylinder.

|
| Fig. 4 Effects of γ on velocity field |
From Fig. 5, we can see that, the velocity increases rapidly initially when the mixed convection parameter (Gr) enhances, while after a large distance from the wall, it vanishes. This is because that larger Gr accompanies stronger buoyancy force, which leads to an increase in the x-component of the velocity. Positive Gr cools the wall or heats the fluid. When Gr ≫ 1, the viscous force is negligible compared with the buoyancy force and the inertial force. When the buoyancy force overcomes the viscous force, the flow starts the transition to the turbulent regime. The boundary layer thickness also increases when Gr increases.

|
| Fig. 5 Effects of Gr on velocity field |
Figure 6 shows that, the effects are negligible when η ∈ [0, 1.5], whereas the velocity increases when η > 1.5. The velocity profiles corresponding to very small α indicate the case of a vertical sheet, for which the fluid experiences the maximum gravitational force. When α changes from π/8 to π/3, the sheet moves from the vertical direction to the horizontal direction. Then, the strength of the buoyancy force decreases, and consequently, the velocity and the boundary layer thickness decrease.

|
| Fig. 6 Effects of α on velocity field |
From Figs. 7 and 8, we can see that, the temperature field increases when β or Re increases. This is due to the fact that larger Re implies that the inertial force plays a dominant role in comparison with the viscous force. From Fig. 9, we can see that the variation in the temperature profile near the wall is negligible, but increases remarkably when 2.5 < η < 8. Figure 10 displays two different cases, i.e., constant thermal conductivity and variable thermal conductivity. It can be seen that the temperature profile increases when " increases. As expected, the temperature increases when R increases (see Fig. 11). Physically, larger R implies larger surface heat flux and thereby warmer fluid, resulting in the increase in the temperature. From Fig. 12, we can see that, the thermal conductivity decreases when Pr increases, and thereby the variations of the thermal characteristics increase. This results in the reduction in the thermal boundary layer thickness and the increase in the heat transfer rate at the bounding surface.

|
| Fig. 7 Effects of β on temperature field |

|
| Fig. 8 Effects of Re on temperature field |

|
| Fig. 9 Effects of γ on temperature field |

|
| Fig. 10 Effects of ε on temperature field |

|
| Fig. 11 Effects of R on temperature field |

|
| Fig. 12 Effects of Pr on temperature field |
The numerical values of the skin friction coefficient and the local Nusselt number are shown in Tables 2 and 3, respectively. It can be seen that the magnitude of the skin friction coefficient increases when β, Re, α, and Gr increase. The effects of β and Re on the heat transfer coefficient are not significant because these parameters do not directly appear in the energy equation. The magnitude of the heat transfer rate at the surface decays when R and ε increase. However, the opposite behavior is observed when Pr increases.
The heat transfer in the couple stress fluid flow due to an inclined stretching cylinder is analyzed in the presence of variable thermal conductivity and radiation effects. The main findings are summarized as follows:
(i) The dimensionless radial velocity f′(η) decays when the couple stress parameter β and the Reynolds number Re increase.
(ii) The effects of the curvature parameter γ and the mixed convection parameter Gr are qualitatively similar.
(iii) The velocity increases when the inclination angle α increases.
(iv) The temperature increases when the couple stress parameter β increases.
(v) The temperature and thermal boundary layer thickness increase when γ and Re increase.
(vi) The temperature and thermal boundary layer thickness increase whereas the heat transfer rate at the surface decreases when ε and R increase.
(vii) The skin friction coefficient in the radial direction decreases when β and Re increase.
| [1] | Fetecaua, C., Mahmood, A., and Jamil, M. Exact solutions for the flow of a viscoelastic fluid induced by a circular cylinder subject to a time dependent shear stress. Communications in Nonlinear Science and Numerical Simulation, 15, 3931-3938 (2010) |
| [2] | Turkyilmazoglua, M. and Pop, I. Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. International Journal of Heat and Mass Transfer, 57, 82-88 (2013) |
| [3] | Malik, M. Y., Hussain, A., and Nadeem, S. Boundary layer flow of an Eyring-Powell model fluid due to a stretching cylinder with variable viscosity. Scientia Iranica, 20, 313-321 (2013) |
| [4] | Hatami, M. and Ganji, D. D. Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders. Journal of Molecular Liquids, 188, 155-161 (2013) |
| [5] | Ellahi, R. and Riaz, A. Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Mathematical and Computer Modelling, 52, 1783-1793 (2010) |
| [6] | Akgül, M. B. and Pakdemirli, M. Lie group analysis of a non-Newtonian fluid flow over a porous surface. Scientia Iranica, 19, 1534-1540 (2012) |
| [7] | Jalil, M., Asghar, S., and Mushtaq, M. Analytical solutions of the boundary layer flow of power-law fluid over a power-law stretching surface. Communications in Nonlinear Science and Numerical Simulation, 18, 1143-1150 (2013) |
| [8] | Mishra, S. R., Dash, G. C., and Acharya, M. Mass and heat transfer effect on MHD flow of a visco-elastic fluid through porous medium with oscillatroy suction and heat source. International Journal of Heat and Mass Transfer, 57, 433-438 (2013) |
| [9] | Rashad, A. M., El-Hakien, M. A., and Abdou, M. M. M. Natural convection boundary layer of a non-Newtonian fluid about a permeable vertical cone embedded in a porous medium saturated with a nanofluid. Computers and Mathematics with Applications, 62, 3140-3151 (2011) |
| [10] | Sahoo, B. Effects of partial slip, viscous dissipation and Joule heating on von Kármán flow and heat transfer of an electrically conducting non-Newtonian fluid. Communications in Nonlinear Science and Numerical Simulation, 14, 2982-2998 (2009) |
| [11] | Zheng, L., Ting, L., and Zhang, X. Boundary layer flow on a moving surface in otherwise quiescent pseudo-plastic non-Newtonian fluid. Journal of University of Science and Technology Beijing, 15, 241-244 (2008) |
| [12] | Turkyilmazoglu, M. The analytic solution of mixed convection heat transfer and fluid flow of an MHD viscoelastic fluid over a permeable stretching surface. International Journal of Mechanical Sciences, 77, 263-268 (2013) |
| [13] | Awais, M., Hayat, T., Qayyum, A., and Alsaedi, A. Newtonian heating in a flow of thixotropic fluid. European Physical Journal-Plus, 128, 144 (2013) |
| [14] | Hayat, T., Awais, M., Safdar, A., and Hendi, A. A. Unsteady three dimensional flow of couple stress fluid over a stretching surface with chemical reaction. Nonlinear Analysis: Modelling and Control, 17, 47-59 (2012) |
| [15] | Hayat, T., Mustafa, M., Iqbal, Z., and Alsaedi, A. Stagnation-point flow of couple stress fluid with melting heat transfer. Applied Mathematics and Mechanics (English Edition), 34, 167-176 (2013) DOI 10.1007/s10483-013-1661-9 |
| [16] | Nadeem, S., Rehman, A., Lee, C., and Lee, J. Boundary layer flow of second grade fluid in a cylinder with heat transfer. Mathematical Problems in Engineering, 2012, 640289 (2012) |
| [17] | Misra, M., Ahmad, N., and Siddiqui, Z. U. Unsteady boundary layer flow past a stretching plate and heat transfer with variable thermal conductivity.World Journal of Mechanics, 2, 35-41 (2012) |
| [18] | Anselm, O. O. and Koriko, K. O. Thermal conductivity and its effects on compressible boundary layer flow over a circular cylinder. International Journal of Recent Research and Applied Studies, 15, 89-96 (2013) |
| [19] | Liao, S. J. Notes on the homotopy analysis method: some definitions and theorems. Communications in Nonlinear Science and Numerical Simulation, 14, 983-997 (2009) |
| [20] | Hayat, T., Qayyum, A., Alsaadi, F., Awais, M., and Dobaie, A. M. Thermal radiation effects in squeezing flow of a Jeffery fluid. European Physical Journal-Plus, 128, 85 (2013) |
| [21] | Ramzan, M., Farooq, M., Alsaedi, A., and Hayat, T. MHD three-dimensional flow of couple stress fluid with Newtonian heating. European Physical Journal-Plus, 128, 49 (2013) |
| [22] | Abbasbandy, S., Hashemi, M. S., and Hashim, I. On convergence of homotopy analysis method and its application to fractional integro-differential equations. Quaestiones Mathematicae, 36, 93-105 (2013) |
| [23] | Rashidi, M. M., Anwar Bég, O., Kavyani, N., and Islam, M. N. Entropy generation in hydromagnetic convective von Karman swirling flow: homotopy analysis. International Journal of Applied Mathematics and Mechanics, 9, 37-65 (2013) |
| [24] | Noor, N. F. M. and Hashim, I. Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 53, 2044-2051 (2010) |
| [25] | Turkyilmazoglu, M. and Pop, I. Exact analytical solutions for the flow and heat transfer near the stagnation point on a stretching/shrinking sheet in a Jeffrey fluid. International Journal of Heat and Mass Transfer, 57, 82-88 (2013) |
 2016, Vol. 37
2016, Vol. 37




