Article Information
- Yuhong ZENG, Wenxin HUAI, Mingdeng ZHAO. 2016.
- Flow characteristics of rectangular open channels with compound vegetation roughness
- Appl. Math. Mech. -Engl. Ed., 37(3): 341-348
- http://dx.doi.org/10.1007/s10483-016-2035-6
Article History
- Received Mar. 12, 2015;
- in final form Aug. 13, 2015
Vegetation is an important component for natural rivers. Aquatic vegetation can affect the flow characteristics together with the channel geometry and the bed composition[1]. Nowa- days, humans have clearly realized that aquatic vegetation can effectively benefit the ecological restoration, and thus have selectively planted more vegetation into rivers, lakes, and ponds to improve the water quality and the surrounding environments. Vegetation can grow homoge- neously, but more often is found to grow heterogeneously. For example, vegetation gaps or patches are very common in natural channels[2]. Sometimes, vegetation may uniformly cover half of the channel bed, such as riparian vegetation and vegetated flood plain. Under this sit- uation, the variation of the vegetation across the lateral direction of the channel can cause two flow lanes, which we idealize as a parallel flow here.
The most well-known parallel flow occurs in compound channels. With a varied water depth across the channel, there is a fast moving flow in the deeper main channel and a slow moving flow in the shallower flood plain, and the velocity difference can generate mixing layers ad- jacent to the interface between the main channel and the flood plain[3]. In the past years, a large amount of researches have been focused on the flow characteristics of compound channels. Tominaga and Nezu[4] investigated the secondary flow in compound channels, and discussed its effects on the momentum transfer and boundary shear stress. Wang and Cheng[5] investigated the secondary flows generated by longitudinal bedforms, and presented an analytical descrip- tion for different patterns of the secondary flow structures. Spooner and Shiono[6] measured the velocity and boundary shear stress of a meandering overbank flow. Shiono and Feng[7] conducted experiments in both rectangular and compound channels to investigate the effects of the secondary flow on solute mixing. Van Prooijen et al.[8] adopted the eddy viscosity concept to analyze the momentum exchange between the flood plain and the main channel, and pointed out that the lateral momentum transfer was mainly caused by the horizontal coherent vortex and the bottom turbulence, and the effect of the secondary effect could be neglected.
To investigate the lateral transfer of the streamwise momentum caused by different bed compositions, Vermaas et al.[9] conducted laboratory experiments in a rectangular channel, half of which was covered by a homogeneous layer of stone with D50 = 7.6mm, and the other half was covered by polished wooden plates so as to create a smooth bed. After comparing the effects of the turbulent mixing, secondary current, and horizontal coherent vortex on the lateral transfer of the streamwise momentum, they concluded that when the water depth was small, the turbulent mixing was the main factor for the lateral momentum exchange, while when the water depth was large, the secondary current was the dominate factor.
For the parallel flow caused by the lateral vegetation roughness, Darby[10] presented a modi- fied hydraulic model to predict the stage-discharge curves for the channels with riparian vegeta- tion based on the momentum and continuity equations accounting for the lateral shear. White and Nepf[11] analyzed the two-layer-structure of the open channel partially covered with emer- gent vegetation, and observed that the coherent vortices spanned both the flow layers, which were the dominant contributors to the lateral momentum fluxes. Pasche and Rouve[12] inves- tigated the flow in a compound channel with vegetation on the flood plain, and predicted the flow resistance via some basic flow parameters. However, in their study, the vegetation in one of the lanes was at its upper extreme, which inhibited the vertical circulation. In this paper, the characteristics of the parallel flows caused by a lateral bed roughness difference due to the partial submerged vegetation across the channel are experimentally and theoretically studied.
2 Experimental setup 2.1 Flume setupThe experiments are conducted in a straight and rectangular flume constructed in the Hy- draulic Laboratory of Wuhan University. The glass recirculating flume is 0.6m wide (B) and 20m long, and the bed slope is fixed as 0.2%. Water is pumped from an underground reservoir to a 20m high water tank, and then overflows into the flume through a wave suppressor. The discharge is recorded by an electric magnetic valve with an accuracy of 0.1 L·s-1, and the water surface is adjusted by a tail-gate to keep the flow uniform. The widths of the vegetation half and smooth bed half are both 0.3m. The plastic artificial grass with an average height of 4.5 cm is covered on the vegetation half (see Fig. 1), which consists of four branches, and the diameter of each branch with six leaves is about 1mm. The grass are positioned in a parallel pattern with a density m = 2 000 stems per m2.

|
| Fig. 1 Experimental setup |
The instaneous 3D flow velocities are measured by a 16MHz acoustic Doppler velocimeter (micro ADV) system equipped with an upward probe and a downward probe. The velocity data are recorded at 50Hz for 2 minuets at every position, which means that 6 000 data are collected. The ADV measurements range from 0.005m beneath the water surface to 0.005m above the channel bottom.
Shiono and Knight[13] pointed out that the misalignment of the ADV could cause an error in the velocity measurement. Therefore, during the measurement, the appropriate alignment of the ADV is very important, and the x-direction is defined according to the direction of the time- and space-averaged velocity vectors in a cross section with the uniform flow. The measurement uncertainty cannot be avoided because of the Doppler noise, the finite measurement volume, and the limited accuracy in solving the Doppler phase shift[14]. To avoid the measurements with poor correlations, a tiny particle solution is added to improve the measurement accuracy.
2.3 Experimental casesTwo turbulent flow cases are investigated (see Table 1), where the Reynolds number Re is defined by
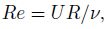
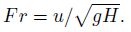
Six cross sections (x = -0.6m, 0.2m, 1.5m, 2.5m, 5.5m, 10.5m) are selected (see Fig. 2). On each cross section, seven vertical lines are measured. The vertical measuring intervals are set to be within the range from 1 cm to 5 cm. For the zones near the channel bottom and the water surface, a finer interval 0.5 cm is adopted.

|
| Fig. 2 Measuring arrangement |
Figure 3 shows the vertical profile of the streamwise velocity u of Case A1 at Line CS-0. The flow is approximately uniform along the lateral direction, and its distribution nearly conforms to a logarithmic law. For most open channel flows, the horizontal maximum velocity occurs at the center of the channel, but here it does not. The velocity on the vegetation side is much larger than that on the non-vegetation side, and it is evident that the vegetation started from x = 0 has effects on the upstream flow (x = -0.6m). Limited by the measuring device, here we have not measured the velocity at the water surface, but we can conclude from the measurement that the velocity begins to decrease at some point below the water surface. This shows that the maximum velocity always occurs at a point below the water surface.

|
| Fig. 3 Vertical profile of streamwise velocity at Line CS-0 |
Figure 4 presents the longitudinal development of u on the vegetation lane (y = 15 cm) and the non-vegetation lane (y = 45 cm). The vegetation retards the flow, and parts of the current are pushed into the non-vegetation half, making the streamwise velocity become larger and larger on the non-vegetation half while become smaller and smaller on the vegetation half. At Line CS-4, the velocity distribution is almost constant, indicating that the flow can be regarded as fully developed. The vertical profile on the vegetation looks similar to that over submerged vegetation. There is a typical exchange zone at the vegetation top (z = 4.5 cm) and a classic wake zone under z = 3 cm.

|
| Fig. 4 Vertical profile of longitudinal velocity u |
According to van Prooijen et al.[8], the width of the mixing layer δ is defined as two times of the distance between y25%, where the depth-averaged streamwise velocity
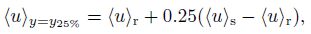
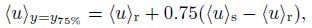
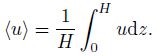
For Line CS-4 of Case A1, δ is estimated as 7.0 cm. From Fig. 5, we can see that the mixing layer is located on the non-vegetation side. Similarly, δ for Case A2 is estimated as 7.4 cm, and is located on the non-vegetation side too. It means that the secondary circulation playing a role in the mixing layer spreads over the non-vegetation side, which agrees with the research of Vermass et al.[9] who concluded that the secondary circulation caused by the lateral roughness transition across the channel was mainly located on the smooth side. Here, the aspect ratio (B/H) is small (3.75 for Case A1 and 3.33 for Case A2). Therefore, the effects of the side wall cannot be ignored. In other words, the mixing layer is the result of the joint action of the secondary currents caused by the side wall and the roughness variation across the channel.

|
| Fig. 5 Lateral variation of depth-averaged longitudinal velocity $\left\langle u \right\rangle $ for Line CS-4 of Case A1 |
The Reynolds stress (-u′w′) of Case A1 at Line CS-4 is plotted in Fig. 6. It can be seen that, on the vegetation bed (y = 15 cm), the maximum value appears at the top of the vegetation, which is similar to the flow over submerged vegetation. On the non-vegetation bed (y = 45 cm), the location of the maximum value of the Reynolds stress is close to the channel bottom (under 2 cm), and it is much smaller than that on the vegetation half, which indicates that the turbulence caused by the vegetation is much stronger than that caused by the channel bottom roughness.

|
| Fig. 6 Vertical variations of Reynolds stress for Case A1 |
Under the combined action of the turbulence and lateral shear caused by the bottom vegeta- tion, large coherent structures occur around the interface between the vegetation lane and the non-vegetation lane, which has larger length and time scales than those of the bottom induced turbulence (see Refs. [8] and [15]). As Fig. 4 shows, there is an exchange zone around the vege- tation top. We use the measured data for Case A1 at z = 4 cm (y = 15 cm) for the analysis, and plot the result in Fig. 7 (both signals have been smoothed by a one-second moving average). The time series of the streamwise and the product of the streamwise and transverse velocity fluctuations show large scale motion with small scale fluctuation. The streamwise velocity oscil- lates strongly at a frequency approximately 0.14Hz, which is close to the result 0.11Hz obtained by Ghisalberti and Nepf[16] for an exchange zone of a flexible experimental canopy. The dif- ference proves that the motion of the vortices can be affected by the vegetation rigidity, density, water depth, etc. In the time series of turbulent momentum transport, a sweep (u′ > 0, w′ < 0) is followed by an ejection (u′ < 0, w′ > 0) such that the momentum transport oscillates as twice of the vortex frequency (0.28Hz). As mentioned above, there is an exchange zone around the vegetation canopy, and the vertical transport is dominated by the highly structured coherent vortices[16].

|
| Fig. 7 Time series of streamwise velocity (u, dashed line) and vertical momentum transport per unit area per unit fluid density (u′w′, solid line) for Line CS-3 of Case A1, where y = 15 cm, and z = 4 cm |
To elucidate the impact of vegetation on the turbulence structure, a quadrant analysis is performed to investigate the contribution of the outward interaction (Q1, u′ > 0, and w′ > 0), the inward interaction (Q3, u′ < 0, and w′ <0), the ejection (Q2, u′ < 0, and w′ > 0), and the sweep (Q4, u′ > 0, and w′ < 0) to the Reynolds stress. Figure 8 shows the Reynolds stress acting on the interface between the vegetation lane and the non-vegetation lane for Case A1. At the entrance of the parallel flow (Line CS-0 in Fig. 8), the four actions are almost the same along the water depth, and the comparative ejection action is the most obvious. At Line CS-4, the sweep action is the dominant under the vegetation, and it achieves its maximum at the top of the vegetation. Above the vegetation top, the ejection action is the dominant. This phenomenon is similar to that investigated by Ghisalberti and Nepf[16] in the open channels with submerged vegetation. Moreover, one can find that around z = 4.5 cm, there is a swing around the vegetation height which may be caused by the waving motion of plants under the action of the streamwise velocity oscillation and the inherent spatial variation of the vegetation.

|
| Fig. 8 Stress contribution from four quadrants |
In this paper, an idealized parallel flow caused by partially submerged vegetation across a channel is investigated experimentally. For the vegetated lane, the vertical distributions of the longitudinal velocity and the Reynolds stress are similar to those in a channel fully covered by submerged vegetation. A quadrant analysis shows that: under the vegetation, the sweep action is the dominant, and achieves its maximum at the top of the vegetation; while above the vegetation top, the ejection action is the dominant. On the non-vegetation lane, the vertical profile of the streamwise velocity approximately conforms to the logarithmic law, and the vertical distributions of the longitudinal velocity and the Reynolds stress are similar to those of a free open channel flow. The mixing layer is located on the non-vegetation lane, and its width is larger than 10% of the channel width, which shows that the effect of vegetation is the dominant compared with the bed roughness. Here, only a qualitative analysis has been made on the characteristics of the parallel flow caused by the lateral vegetation roughness variation, and a quantitative analysis will be conducted to reveal the mechanism of the lateral momentum exchange in the future.
| [1] | Wang, W. J., Huai, W. X., Zeng, Y. H., and Zhou, J. F. Analytical solution of velocity distri- bution for flow through submerged large deflection flexible vegetation. Applied Mathematics and Mechanics (English Edition), 36(1), 107-120 (2015) DOI 10.1007/s10483-015-1897-9 |
| [2] | Folkard, A. M. Flow regimes in gaps within stands of flexible vegetation: laboratory flume simu- lations. Environmental Fluid Mechanics, 11, 289-306 (2011) |
| [3] | Stephenson, D. and Kolovopoulos, P. Effects of momentum transfer in compound channels. Journal of Hydraulic Engineering, 116, 1512-1522 (1990) |
| [4] | Tominaga, A. and Nezu, I. Turbulent structure in compound open-channel flows. Journal of Hydraulic Engineering, 117, 21-41 (1991) |
| [5] | Wang, Z. Q. and Cheng, N. S. Time-mean structure of secondary flows in open channel with longitudinal bed forms. Advances in Water Resources, 29, 1634-1649 (2006) |
| [6] | Spooner, J. and Shiono, K. Modelling of meandering channels for overbank flow. Proceedings of the Institution of Civil Engineers, Water & Maritime Engineering, 156, 225-233 (2003) |
| [7] | Shiono, K. and Feng, T. Turbulence Measurements of dye concentration and effects of secondary flow on distribution in open channel flows. Journal of Hydraulic Engineering, 129, 373-384 (2003) |
| [8] | Van Prooijen, B., Battjes, J., and Uijttewaal, W. Momentum exchange in straight uniform com- pound channel flow. Journal of Hydraulic Engineering, 131, 175-183 (2005) |
| [9] | Vermaas, D. A., Uijttewaal, W. S. J., and Hoitink, A. J. F. Lateral transfer of streamwise mo- mentum caused by a roughness transition across a shallow channel. Water Resources Research, 47, 1-12 (2011) |
| [10] | Darby, S. E. Effect of riparian vegetation on flow resistance and flood potential. Journal of Hydraulic Engineering, 125, 443-454 (1999) |
| [11] | White, B. L. and Nepf, H. M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resources Research, 44, 1-15 (2008) |
| [12] | Pasche, E. and Rouve, G. Overbank flow with vegetatively roughened flood plains. Journal of Hydraulic Engineering, 111, 1262-1278 (1985) |
| [13] | Shiono, K. and Knight, D. W. Turbulent open-channel flows with variable depth across the chan- nel. Journal of Fluid Mechanics, 222, 617-646 (1991) |
| [14] | Voulgaris, G. and Trowbridge, J. H. Evaluation of the acoustic Doppler velocimeter (ADV) for turbulence measurement. Journal of Atmospheric and Oceanic Technology, 15, 272-289 (1998) |
| [15] | Knight, D. W. and Shiono, K. Turbulence measurements in a shear layer region of a compound channel. Journal of Hydraulic Research, 28, 175-196 (1990) |
| [16] | Ghisalberti, M. and Nepf, H. The structure of the shear layer in flows over rigid and flexible canopies. Environmental Fluid Mechanics, 6, 277-301 (2006) |
 2016, Vol. 37
2016, Vol. 37



