Article Information
- Luyu SHEN, Changgen LU. 2016.
- Boundary-layer receptivity under interaction of free-stream turbulence and localized wall roughness
- Appl. Math. Mech. -Engl. Ed., 37(3): 349-360
- http://dx.doi.org/10.1007/s10483-016-2037-6
Article History
- Received Mar. 23, 2015;
- in final form Jul. 10, 2015
2. School of Marine Science, Nanjing University of Information Science and Technology, Nanjing 210044, China
Turbulence is the basic flow state in nature. However, it has still not been well understood. The prediction of the laminar-turbulent transition is very important to the design and man- ufacture of vehicles, ships, and aircrafts. According to the classical stability theory, at low turbulence level, unstable Tollmien-Schlichting (T-S) waves are first excited in the boundary layers, and then grow linearly until a breakdown occurs. Receptivity establishes the initial con- ditions of the amplitude, the frequency, the wave number, and the phase for the breakdown of the laminar flow[1]. Current understanding shows that the boundary-layer receptivity to acous- tic and vortical disturbances occurs in the regions where there is a rapid streamwise variation in the mean-flow such as at the leading edge of the flat-plate[2] and at the wall roughness[3].
Alzin and Polyakov[4] demonstrated the local receptivity mechanism by experiments, and measured a linear increase in the receptivity with the acoustic forcing and roughness height. Goldstein[3] and Ruban[5] independently showed that the local short-scale mean flow distortion due to a roughness element was capable to excite the short-wavelength T-S waves with long- wavelength acoustic waves, i.e., the wavelength conversion mechanism.
For the vortical receptivity, Rogler and Reshotko[6] modeled the free-stream disturbances as an array of counter-rotating convected vortices to analyze the boundary-layer response. Zavol’skii et al.[7] noted that the most effective T-S wave excitation occurred at the resonance condition
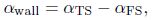
Many studies on vortical receptivity involve single-frequency vortical disturbances[12, 13, 14], whereas the studies on the receptivity to broadband free-stream turbulence (FST) are relatively less. In this paper, the boundary-layer receptivity under the interaction of FST and localized wall roughness is studied by the DNS and fast Fourier transformation. The obtained results agree well with Dietz’s experiments[11, 12] and Zhang and Zhou’s numerical data[14].
2 Governing equations and numerical methods 2.1 Governing equationsThe dimensionless Navier-Stokes equations are
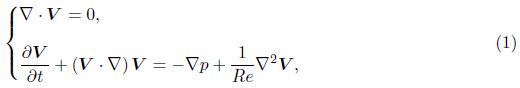
High-order finite difference schemes are introduced to discretize the governing equations (1). For the time integration, a modified fourth-order Runge-Kutta scheme is employed[15]. A spectral method is used for the x-direction discretization, and non-uniform compact finite difference schemes are used for the y-direction discretization. The detail is presented in Ref. [16].
2.3 Free-stream turbulence modelThe mathematical model[17] is introduced to generate the FST, which is represented by
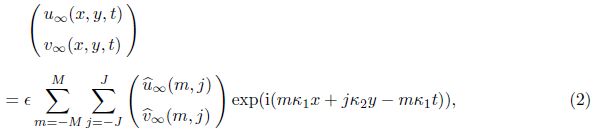
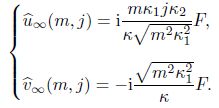
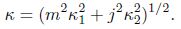
The computational domain is the shadow area in Fig. 1. The length of the domain is X = 2.0 × 2π/κ1 so that the generated waves cannot reach the exit and the height of the domain Y = 14.39 is five times of the boundary-layer thickness:
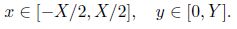

|
| Fig. 1 Computational domain |
The roughness element is placed at the location X/16 from the entrance. 1 024 × 200 grids are arranged in the x-direction and the y-direction, respectively. The grids in the x-direction are uniform. The refined grids are utilized near the wall in the y-direction, which are given by
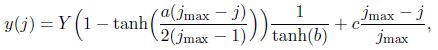
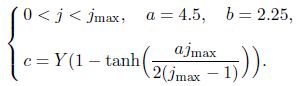
According to Ref. [17], the perturbation velocity of the imposed FST at the upper boundary is
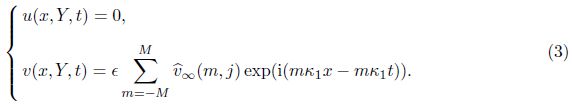
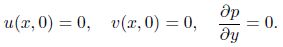

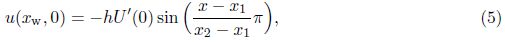
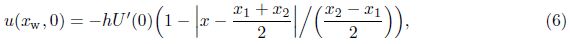
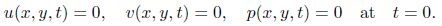
In this section, we focus on the boundary-layer receptivity to the FST interacting with the localized wall roughness. The amplitude of the FST is set to 0.001, and a rectangle hump of the height 0.05 and the width X/128 is added to the surface of the plate. Hereafter, ω and α are the frequency and the streamwise wave number, respectively.
As shown in Fig. 2, a group of generated perturbation wave packets are observed at the Reynolds number 800, which is determined by a subtraction of the result computed above a smooth plate from a similar numerical result with the localized wall roughness, where the arrows in the figures point at the roughness location. Figure 2(a) plots the spatial evolu- tion of the perturbation wave packets in the boundary layer at t = 1 050, and its amplitude increases in the streamwise direction. Figure 2(b) gives the temporal evolution of the wave packet at a fixed point x = -150 in the boundary layer, whose amplitude is constant over time. According to the evolution of the wave packets, the positions of the peaks and valleys are tracked over time to calculate the propagation speed by taking the average. The propagation speed of the wave packets is 0.370.

|
| Fig. 2 Spatial evolution and temporal evolution of wave packets in boundary layer at Re = 800 |
Then, a group of perturbation waves are separated from the wave packets in Fig. 2(a) by the fast Fourier transformation. The spatial evolutions of these stability, neutral, and instability waves are plotted in Figs. 3(a), 3(b), and 3(c), respectively. According to the spatial evolutions, the frequencies, the wavelengths, and the growth rates (or decaying rates) of the isolated waves can be estimated by the averages of the periods, the distances between the peaks/valleys and the neighbor peaks/valleys, and the amplitude ratios of the peaks/valleys to their neighbor peaks/valleys.

|
| Fig. 3 Spatial evolution of generated waves at Re = 800 |
The excited wave packets at the Reynolds numbers 520, 800, and 1 000 are treated in the same way, and the results are presented in Tables 1, 2, and 3. As shown in Tables 1, 2, and 3, the generated perturbation waves in the boundary layer have different dispersion relations from those of the imposed FST. They share the same frequencies, but the gener- ated waves have shorter wavelengths (or larger wave numbers), which confirms the wavelength conversion mechanism for the receptivity[9, 12, 13]. Moreover, the dispersion relations of the excited perturbation waves are identical with the theoretical solutions of the T-S waves ob- tained from the Orr-Sommerfeld (O-S) equation, and the errors between them are less than 10-4. In addition, at the critical Reynolds number 520, only one neutral wave is excited (see Table 1). At the Reynolds number 800, the frequencies of the excited neutral waves are ω = 0.066 20 and ω = 0.136 24, which are exactly on the lower and upper branches of the neutral stability curve, and the frequencies of the excited instability waves are within these two branches (see Table 2). Similarly, at the Reynolds number 1 000, the frequencies of the excited instability waves are ω = 0.054 48 and ω = 0.130 00, which are exactly on the lower and upper branches of the neutral stability curve, and the frequencies of the excited instability waves are within these two branches (see Table 3). These results agree with the theoretical solutions of the neutral stability curve. Furthermore, the parameters of the free-stream turbulence model of the upper and lower branches in Tables 1, 2, and 3 are arbitrarily selected. In theory, an infinite number of small perturbation waves can be chosen. For calculational feasibility, we only consider the free-stream turbulence model consisting of a finite number of small perturbation waves, interacting with the wall roughness to generate T-S waves in the boundary layer. These indirectly validate the randomness of the free-stream turbulence, and also illustrate that the proposed free-stream turbulence model has the features of natural turbulence.

|

|

|
The neutral wave when α = (0.124 00, 0.000 00) and ω = 0.311 25 is selected from Table 1 as an example for the discussion, and Fig. 4 gives a rigorous comparison between the amplitude and phase of the neutral wave and the solutions of the O-S equation. The results agree perfectly with each other.

|
| Fig. 4 Amplitudes and phases of generated perturbation wave when Re = 520, t = 950, and x = −200 |
The frequencies, wave numbers, growth rates (or decaying rates), amplitudes, and phases of the generated perturbation waves do match the theoretical solutions of T-S waves obtained from the O-S equation. It demonstrates that the T-S wave packets superposed by a group of stability, neutral, and instability T-S waves are excited by the FST interacting with the localized wall roughness, thus confirming that boundary-layer receptivity exists.
Furthermore, the computed propagation speed of the T-S wave packets in the boundary layer is 0.391, 0.370, and 0.350 with the Reynolds numbers of 520, 800, and 1 000, respectively, which is approximately one-third of the free-stream velocity, closely matching the propagation speeds of the T-S wave packets measured by Dietz[11]. The phase speed of the neutral T-S waves in Table 1 is 0.398, and the phase speeds of the most unstable T-S wave in Tables 2 and 3 are 0.367 and 0.355, respectively. It indicates that the propagation speeds of the T-S wave packets are largely determined by the phase speeds of the most unstable T-S waves.
3.2 Receptivity response to forcing amplitude, roughness height and widthDietz’s experiment data[12], Wu’s theoretical study[13], and Zhang and Zhou’s numerical results[14] have verified that for single-frequency vortical disturbances interacting with localized wall roughness, the receptivity response is linear within a specific range. The linear receptivity formula is

The Reynolds number is accordingly set to the same as that in Dietz’s experiment[12]. In Figs. 5 and 6, |u0| is the amplitude of the excited T-S wave in the boundary layer when
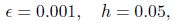

|
| Fig. 5 Variations of amplitude of excited T-S wave with amplitude of imposed free-stream turbulence and non-dimensional roughness height: △ ω = 0.026 62, α = (0.091 63, 0.010 85); ■ ω = 0.053 24, α = (0.165 86, −0.000 56); o ω = 0.079 86, α = (0.232 77, −0.007 25); - - linear variation; × Dietz’s measurements |
The spatial Fourier transformation of the roughness geometry evaluated at (αTS - αFS) for a single rectangle hump is given by
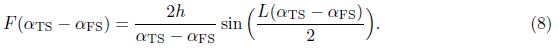

|
| Fig. 6 Variations of amplitude of excited T-S wave with roughness width: - - sin(L(αTS−αFS)/2); △ ω = 0.026 62, α = (0.091 63, 0.010 85); ■ ω = 0.053 24, α = (0.165 86, −0.000 56); o ω = 0.079 86, α = (0.232 77, −0.007 25); × Dietz’s measurements |

|
| Fig. 7 Variations of excited T-S wave ver- sus Fourier transformation of rough- ness geometry at αTS − αFS: - - lin- ear variation; △ ω = 0.026 62, α = (0.091 63, 0.010 85); ■ ω = 0.053 24, α = (0.165 86, −0.000 56); o ω = 0.079 86, α = (0.232 77, −0.007 25) |
In conclusion, Eq. (7) is demonstrated to be also valid for the multi-frequency T-S waves generated by the FST interacting with the localized wall roughness when the forcing amplitude is less than 1% of the free-stream velocity and the non-dimensional height h*/δr is less than 0.2.
3.3 Receptivity response to different roughness geometriesThe receptivity response to different roughness geometries is studied under the FST. Six different roughness geometries (rectangle, sine, and triangle humps/gaps) are solely added on the wall with the same cross-section area. The heights of the rectangle, sine, and triangle hump/gap are
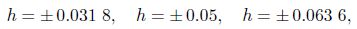
As shown in Table 4, the dispersion relations of the T-S waves excited by the roughness elements of different geometries are almost identical, which also agree well with the solutions of the O-S equation. It indicates that the dispersion relations of the generated T-S waves cannot be changed by varying the geometry of the roughness elements. However, the variations of the roughness geometries are able to change the phases and amplitudes of the generated T-S waves. As seen in Fig. 8, the T-S waves with opposite phases are generated by a sine hump and a sine gap, respectively, and the amplitudes of the T-S waves generated by a sine hump are larger than those generated by a sine gap. Similar conclusions are found with the rectangle and triangle roughness elements.

|

|
| Fig. 8 Spatial evolution of neutral waves (ω = 0.124 00, α = (0.311 20, 0.000 00)) and stability waves (ω = 0.093 00, α = (0.244 54, 0.002 03)) generated by sine hump (solid line) and sine gap (dashed line) when Re = 520 and t = 995.0 |
The boundary-layer receptivity under the interaction of free-stream turbulence and localized wall roughness has been studied by the DNS and fast Fourier transform. The free-stream turbulence model is set up to reflect the nature of real turbulence which is random and consists of multi-frequency and multi-scale fluctuations. As a result, T-S wave packets are observed, which are superposed by a group of stability, neutral, and instability T-S waves excited in the boundary layer. The propagation speeds of the T-S wave packets, which are approximately one-third of the free-stream velocity, are found to be largely determined by the phase speeds of most unstable T-S waves. Rather than the excitation of a single T-S wave[12, 13, 14], the boundary- layer receptivity to the FST in the present study is more universal. The linear receptivity formula is demonstrated to be valid for the multi-frequency T-S waves generated by the free- stream turbulence when the forcing amplitude is up to 1% of the free-stream velocity and the non-dimensional height h*/δr is less than 0.2. These conclusions are similar to those found by Dietz[11, 12] and Zhang and Zhou[14]. Additionally, the effects of the roughness geometries on the receptivity are also studied. It is found that the dispersion relations of the generated T-S waves cannot be changed by varying the geometry of the roughness elements with the same cross-section area and width, whereas the phases and amplitudes of the generated T-S waves are changed.
| [1] | Saric, W. S., Reed, H. L., and Kerschen, E. J. Boundary-layer receptivity to freestream distur- bances. Annual Review of Fluid Mechanics, 34, 291-319 (2002) |
| [2] | Goldstein, M. E. The evolution of Tollmien-Sclichting waves near a leading edge. Journal of Fluid Mechanics, 127, 59-81 (1983) |
| [3] | Goldstein, M. E. Scattering of acoustic waves into Tollmien-Schlichting waves by small streamwise variations in surface geometry. Journal of Fluid Mechanics, 154, 509-529 (1985) |
| [4] | Aizin, L. B. and Polyakov, N. F. Acoustic generation of Tollmien-Schlichting waves over local unevenness of surface immersed in stream. Physics of Fluids, 6, 3705-3716 (1994) |
| [5] | Ruban, A. I. On the generation of Tollmien-Schlichting waves by sound. Fluid Dynamics, 19, 709-717 (1984) |
| [6] | Rogler, H. L. and Reshotko, E. Disturbances in a boundary layer introduced by a low intensity array of vortices. SIAM Journal on Applied Mathematics, 28, 431-462 (1975) |
| [7] | Zavol'skii, N. A., Reutov, V. P., and Rybushkina, G. V. Excitation of Tollmien-Schlichting waves by acoustic and vortex disturbance scattering in boundary layer on a wavy surface. Journal of Applied Mechanics and Technical Physics, 24, 355-361 (1983) |
| [8] | Crouch, J. D. Distributed excitation of Tollmien-Schlichting waves by vortical free-stream distur- bances. Physics of Fluids, 6, 217-223 (1994) |
| [9] | Duck, P. W., Ruban, A. I., and Zhikharev, C. N. The generation of Tollmien-Schlichting waves by free-stream turbulence. Journal of Fluid Mechanics, 312, 341-371 (1996) |
| [10] | Dietz, A. J. Distributed boundary-layer receptivity to convected vorticity. The 27th AIAA Fluid Dynamics Conference, AIAA 1996-2083, New Orleans (1996) |
| [11] | Dietz, A. J. Boundary-layer receptivity to transient convected disturbances. AIAA Journal, 36, 1171-1177 (1998) |
| [12] | Dietz, A. J. Local boundary-layer receptivity to a convected free-stream disturbance. Journal of Fluid Mechanics, 378, 291-317 (1999) |
| [13] | Wu, X. S. Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances: a second-order asymptotic theory and comparison with experiments. Journal of Fluid Mechanics, 431, 91-133 (2001) |
| [14] | Zhang, Y. M. and Zhou, H. Numerical study of local boundary layer receptivity to freestream vortical disturbances. Applied Mathematics and Mechanics (English Edition), 26, 547-554 (2005) DOI 10.1007/BF02466327 |
| [15] | Shen, L. Y., Lu, C. G., Wu, W. G., and Xue, S. F. A high-order numerical method to study three- dimensional hydrodynamics in a natural river. Advances in Applied Mathematics and Mechanics, 7, 180-195 (2015) |
| [16] | Lu, C. G., Cao, W. D., Zhang, Y., and Peng, J. Large eddies induced by local impulse at wall of boundary layer with pressure gradients. Progress in Natural Science, 18, 873-878 (2008) |
| [17] | Zhang, Y. M., Zaki, T., Sherwin, S., and Wu, X. S. Non-linear response of a laminar boundary layer to isotropic and spanwise localized free-stream turbulence. The 6th AIAA Theoretical Fluid Mechanics Conference, AIAA 2011-3292, Hawaii (2011) |
| [18] | Bodonyi, R. J. Non-linear triple-deck studies in boundary-layer receptivity. Applied Mechanics Reviews, 43, S158-S166 (1990) |
| [19] | Saric, W. S., Hoos, J. A., and Radeztsky, R. H. Boundary-layer receptivity of sound with rough- ness. Proceedings of the Symposium, ASME and JSME Joint Fluids Engineering Conference, American Society of Mechanical Engineers, New York (1991) |
| [20] | Zhou, M. D., Liu, D. P., and Blackwelder, R. F. An experimental study of receptivity of acoustic waves in laminar boundary layers. Experiments in Fluids, 17, 1-9 (1994) |
 2016, Vol. 37
2016, Vol. 37


