Shanghai University
Article Information
- Qingkai ZHAO, Hang XU, Longbin TAO, A. RAEES, Qiang SUN. 2016.
- Three-dimensional free bio-convection of nanofluid near stagnation point on general curved isothermal surface
- Appl. Math. Mech. -Engl. Ed., 37(4): 417-432
- http://dx.doi.org/10.1007/s10483-016-2046-9
Article History
- Received Jul. 23, 2015;
- in final form Sept. 18, 2015
2. School of Marine Science and Technology, Newcastle University, Newcastle upon Tyne NE1 7RU, U. K.;
3. Department of Mechanical Engineering, National University of Singapore, 10 Kent Ridge Crescent 119260, Singapore
| a,semi-major radii of curvature tangent | C∞,ambient nanofluid volume fraction; |
| to stagnation point surface; | Cfx,Cfy,local skin friction coefficients along x |
| b,semi-minor radii of curvature tangent | and y-directions,respectively; |
| to stagnation point surface; | DB,Brownian diffusion coefficient; |
| c,ratio of two principal radii of curvature, | DT,thermophoretic diffusion coefficient; |
| c = b/a; | Dm,diffusivity of microorganisms; |
| C,nanoparticle volume fraction; | g,gravitational acceleration; |
| Cw,nanoparticle volume fraction at body | g,vector of gravitational acceleration; |
| surface; | Gr,Grashof number; |
| j,vector of flux of microorganisms; | Qnx,Qny,local wall flux of motile microorgan |
| Le,Lewis number; | microorganisms along x- and y-directions,respec-; |
| N,number density of motile microorgan- | tively; |
| isms; | Rab,bioconvection Rayleigh number; |
| Nw,density of microorganisms at body | Rex,Rey,local Reynolds numbers along x- and |
| surface; | y-directions,respectively; |
| N∞,ambient density of microorganisms; | Sc,Schmidt number; |
| NB,Brownian motion parameter; | T,temperature; |
| Nr,bouncy-ratio parameter; | Tw,temperature at body surface; |
| NT,thermophoresis parameter; | T∞,ambient temperature; |
| Nux,local Nusselt number; | u,v,w,velocity components along x-,y- and |
| p,pressure; | z-axes,respectively; |
| Pr,Prandtl number; | v,velocity vector; |
| Pe, bioconvection P´eclet number; | $\tilde v$,average swimming velocity vector of |
| qwC ,wall mass flux; | gyrotactic microorganisms; |
| qwN ,wall motile microorganism flux; | Wc,maximum cell swimming speed; |
| qwT ,wall heat flux; | x,y,z,Cartesian coordinates; |
| Qmx,Qmy,local wall flux of nanoparticles along | $\tilde v$x,$\tilde v$y,$\tilde v$z,average swimming velocities of gyrotactic |
| x- and y-directions,respectively; | microorganisms. |
| α,thermal diffusivity of nanofluid; | τwx,τwy,local wall skin frictions along x- and y |
| β,volumetric volume expansion coefficient; | directions,respectively; |
| ν,kinematic viscosity,ν = μ/ρf ; | γ,average volume of microorganism; |
| μ,dynamic viscosity; | ε,maximum relative error; |
| ρf ,nanofluid density; | η,similarity variable; |
| ρf∞,ambient base fluid density; | f(η),reduced stream function in x-direction; |
| ρp,nanoparticle density; | s(η),reduced stream function in y-direction; |
| Δρ,density difference between cell and base | θ(η),reduced temperature; |
| fluid,Δρ = ρcell - ρf ; | φ(η),reduced nanoparticle volume fraction; |
| τ ,ratio of effective heat capacity of | ξ(η),reduced density of motile microorgan |
| nanoparticle to that of fluid; | isms. |
In the past several decades,three-dimensional free convection flows in the stagnation point region have received much attention owing to their physical significance and potential industrial applications. Among those studies,Poots[1] found that the flow near a saddle point of attachment is dependent on three factors,namely,the ratio of the two principal radii of curvature at this point,the Prandtl number,and the Grashof number. Based on these findings,the boundary equations were formulated and then solved numerically for a range of values of the ratio of the two principal radii of curvature. Banks[2] made an extension of Poots’s problem[1] to the case where the free convection flows over a nodal point of attachment which corresponds to the negative ratio of the two principal radii of curvature. Ingham et al.[3] considered the time-dependent free convection flow in the stagnation region of a three-dimensional body at large Grashof numbers and presented an approximate series solution valid for small time. Pop and Merkin[4] investigated an unsteady free convection flow near a general three-dimensional stagnation point placed in a fluid-saturated porous medium. They concluded that their solution depends only on the sign of the quantity a+b,where a and b are the principal curvatures of the body at the stagnation point. Slaouti et al.[5] presented an analysis of a time development free convection flow that is caused by a step-change in the wall temperature of a three-dimensional body. Xu et al.[6] formulated an unsteady free convection flow near a three-dimensional stagnation point due to a step-change temperature in the wall using a time-scale which can cover the flow development in the whole time domain.
Recently,many researchers have made efforts to investigate the mechanism of nanofluids [7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17]. Some of them[10, 11, 12, 13, 14, 15, 16, 17] started to consider bioconvection in nanofluids owing to their great potentials in a number of engineering and biotechnological applications,such as in design of biocells and bioconjugates and mass transfer enhancement of microfluids. In such bioconvection applications,insufficient mixing is often a major concern. Traditionally,active mixers have to be used to overcome this flaw,and it is very expensive and high energy-consuming. Moreover,the active mixers can damage biological samples due to the Joule heating generated by themselves. As the next generation of technology,nanofluids are expected to be used for the design of novel microfluidic devices. Hence,bioconvection in nanofluids must be understood at the fundamental level. It is worth noting that Kuznetsov and Avramenko[18] and Kuznetsov and Geng[19] were the first who considered the problem of bioconvection in a suspension containing small solid particles. Their idea was adopted and extended by Geng and Kuznetsov[20, 21] for investigation of diffusivity of small particles suspended in liquids. Very recently,Kuznetsov[10] found that nanofluids can be utilized for enhancement of bioconvection. He therefore proposed a novel theory of nanofluid bioconvection based on the Buongiorno’s mathematical model[11], in which the Brownian diffusion and thermophoresis were taken into account as the important slip mechanisms. Kuznetsov[12] analyzed a bio-thermal convection flow of a nanofluid in suspension of both gyrotactic and oxytactic micro-organisms in a horizontal layer of finite depth. Kuznetsov[13] investigated non-oscillatory and oscillatory bio-thermal convection in a nanofluid suspended with gyrotactic microorganisms. Kuznetsov[14] further discussed the oscillatory instability of the bioconvection of a nanofluid in suspension of both nanoparticles and oxytactic microorganisms. Kuznetsov[15] studied the interaction of oxytactic microorganisms in a shallow horizontal layer of finite depth. Tham et al.[16] considered a mixed bio-convection flow over a sphere embedded in a nanofluid containing both nanoparticles and microorganisms. This idea was further extended by Xu and Pop[17] in their study of mixed nanofluid bioconvection flow past a vertical flat surface.
In this paper,we study the free convection flow in the stagnation region of a three-dimensional body embedded in a nanofluid that contains both nanoparticles and motile gyrotactic microorganisms. By means of Buongiorno’s mathematical model[11],the governing equations describing the conservation of total mass,momentum,thermal energy,nanoparticles,and microorganisms are established and then reduced to a set of fully coupled ordinary differential equations via similarity transformations. The highly efficient HAM-FDM technique (a combination of the homotopy analysis method and the finite difference method) is used to derive the exact solutions to the problem. The influence of various physical parameters on the distribution of motile microorganisms,as well as the physical quantities of practical interest such as the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganism flux are presented and discussed. Several linear regression formulae for estimation of the physical quantities are proposed. It is worth mentioning that the studies involving nanofluid bioconvection are very limited in literature that there is an urgent need to understand the mechanisms of such physical phenomena at a fundamental level.
2 Mathematical descriptionConsider the steady free convection flow of a viscous and incompressible nanofluid that contains both solid particles of nano-size and motile gyrotactic microorganisms in the stagnationpoint region of a three-dimensional body. As shown in Fig. 1,a Cartesian coordinate system (x,y,z) is chosen with its origin O located at the stagnation point,the x- and y-coordinates are measured along the body surface in two directions,respectively,and the z-coordinate is measured normal to the body surface. The stationary surface is kept at the constant distributions for the temperature Tw,the nanoparticle volumetric fraction Cw,and the density of motile microorganisms Nw,while the ambient fluid has the constant values of T∞,C∞,and N∞,respectively. To apply Buongiorno’s mathematical model[11] to this problem,it is assumed that the nanofluid is dilute and the suspended nanoparticles and small microorganisms are kept stable and do not agglomerate in it. Moreover,based on the biological requirement for survival of microorganisms,the base fluid must be water. Furthermore,we assume that the nanoparticles used here have no influence on the swimming direction and the velocity of the microorganisms.

|
| Fig. 1 Physical sketch |
Under the above assumptions,the following five field equations embodying the conservation of total mass,momentum,thermal energy,nanoparticles,and microorganisms are given by

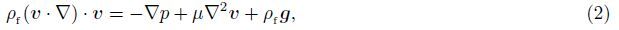
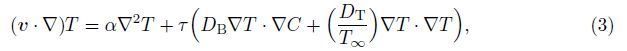
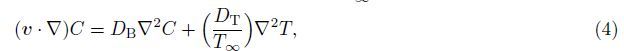




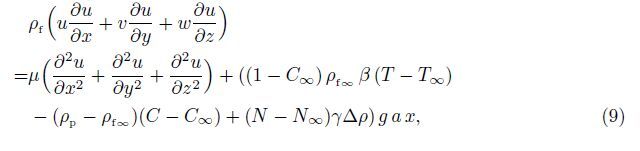
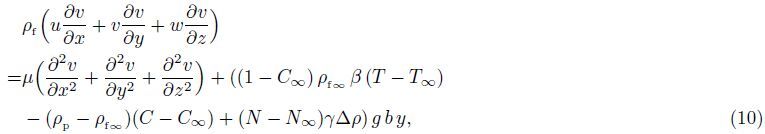
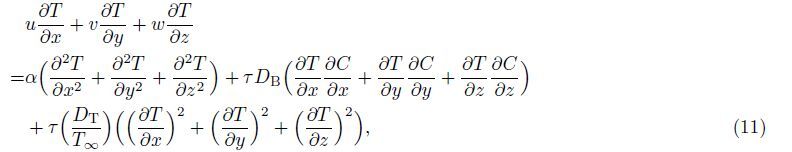
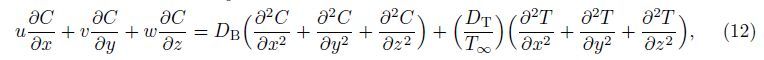

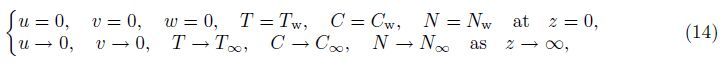
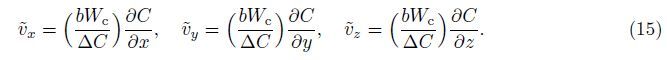
It should be noted here that the direction of gravity g at the lowest stagnation point is perpendicular to the x- and y-directions,while it is inclined to both directions in the vicinity of this key point. This gives rise to the buoyancy induced pressure gradients in the x- and y-directions, but they are negatively small compared to the buoyancy forces in those directions[2, 5]. It should also be noted that the Oberbeck-Boussinesq approximation has been used for linearization of the buoyancy force in Eqs. (9) and (10) with the term ρf∞β(T - T∞) neglected. Therefore,we can just write the components of the buoyancy force in the x-,y-,and z-directions in the forms of
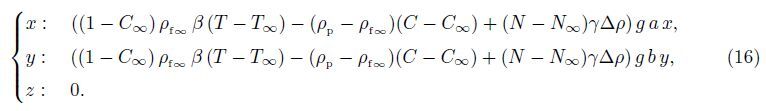
We now define the following similarity variables:
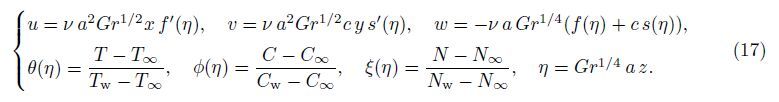
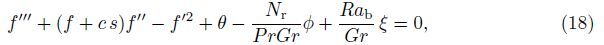
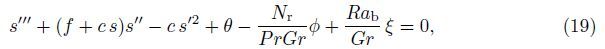
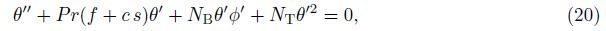
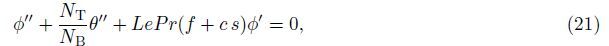
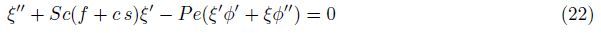
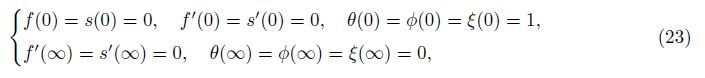
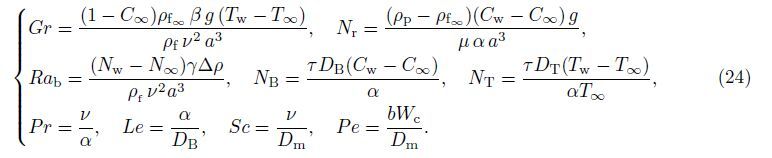
The physically important quantities of practical interest are the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganism flux,which are defined by
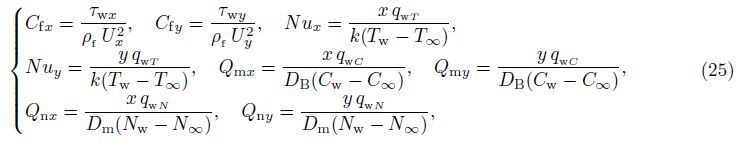
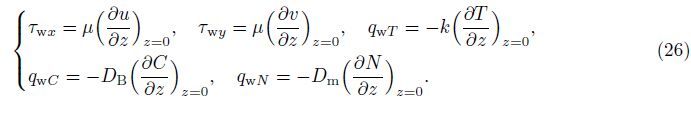
Substituting Eq. (17) into Eq. (25),we obtain
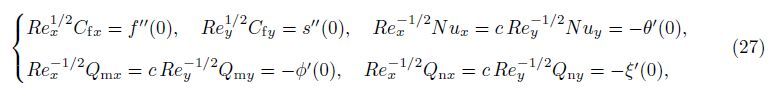
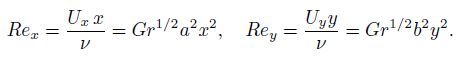
The governing equations (18)-(22) with the associated boundary conditions (23) are solved by the HAM-FDM technique (refer to Appendix A for details). This approach incorporates the merits of high computational efficiency of the FDM and powerful capability for treating strong nonlinearity of the HAM. Therefore,it can be used to simulate nonlinear problems with strong nonlinearity. To check the errors,we define the error function
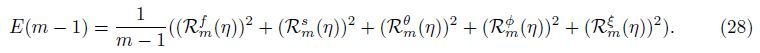

|
| Fig. 2 Comparison of HAM and HAM-FDM results for c = 0.5, NT = 0.3, NB = Nr = 0.1, and Gr = Pr = Le = Rab = Sc = 1.0, where lines are HAM-FDM results (solid line: dimensionless velocity f'(η); dashed line: dimensionless velocity s'(η); dash-dotted line: dimensionless temperature θ(η)), and symbols are HAM results |
 |
We next discuss the influence of various physical parameters on the density of motile microorganisms ξ(η).
As shown in Fig. 3(a),ξ(η) enhances gradually as the buoyancy ratio parameter Nr enlarges. This indicates that either the type of nanoparticle or the difference of nanoparticle volumetric fraction between the wall and the ambient fluid is an important factor to affect the distribution of microorganisms. It is illustrated in Fig. 3(b) that the increase of the thermophoresis parameter NT causes the enhancement of ξ(η). This is to say,the temperature difference between the wall and the ambient fluid has an effect on the distribution of microorganisms,and the larger this value is,the higher the density of microorganisms is. It is also noticed that the inflexion point appears as NT becomes sufficiently large,which moves towards the direction of the longitudinal coordinates with NT continuously increasing. It is found in Fig. 4(a) that the Brownian motion parameter NB exhibits an inverse influence on ξ(η) as compared with NT,its increase leads to the decrease of ξ(η). This can be explained physically that the increase of the difference of nanoparticle volumetric fraction between the wall and the ambient fluid results in the decrease of the density of microorganisms.

|
| Fig. 3 Density of motile microorganisms ξ(η) for various values of bouncy-ratio parameter Nr with NT = NB = 0.1, c = 0.5, and Gr = Pe = Rab = Le = Sc = Pr = 1.0 and for various values of thermophoresis parameter NT with Nr = NB = 0.1, c = 0.5, and Gr = Pe = Rab = Le = Sc = Pr = 1.0 |

|
| Fig. 4 Density of motile microorganisms profile ξ(η) for various values of Brownian motion parameter NB with c = 0.5, Nr = NT = 0.1, and Gr = Pe = Rab = Le = Sc = Pr = 1.0 and for various values of curvature ratio c with Nr = NT = NB = 0.1, and Gr = Pe = Rab = Le = Sc = Pr = 1.0h |
We notice from Fig. 4(b) that ξ(η) reduces monotonously as the curvature ratio c enlarges. This means that one can obtain an appropriate distribution of microorganisms by changing the geometrical shape of the body accordingly. Similarly,it is found from Fig. 5(a) that ξ(η) reduces continuously with the Lewis number Le. As seen in Fig. 5(b),the Prandtl number Pr exhibits different influence on ξ(η) with varying η. When η is small,ξ(η) decreases gradually as Pr increases,while as η becomes sufficiently large,ξ(η) enhances as Pr evolves. The difference of the density of motile microorganisms between the wall and the ambient fluid plays a role on the distribution of microorganisms,which reflects graphically that ξ(η) decreases consecutively as the bioconvection Rayleigh number Rab enlarges,as illustrated in Fig. 6(a). Similar to the effect of Rab on ξ(η),the increase of the Péclet number Pe and the Schmidt number Sc can result in the decrease of ξ(η),as illustrated in Fig. 6(b) and Fig. 7(a). We therefore can alter the density of microorganisms by adjusting the two parameters.

|
| Fig. 5 Density of motile microorganism profile ξ(η) for various values of Lewis number Le with NT = Nr = NB = 0.1, c = 0.5, and Gr = Rab = Pe = Sc = Pr = 1.0 and for various values of Prandtl number Pr with NT = Nr = NB = 0.1, c = 0.5, and Gr = Rab = Le = Sc = Pe = 1.0 |

|
| Fig. 6 Density of motile microorganism profile ξ(η) for various values of bioconvection Rayleigh number Rab with NT = 0.3, Nr = NB = 0.1, c = 0.5, and Gr = Le = Sc = Pr = 1.0 and for various values of bioconvection Péclet number Pe with NT = Nr = NB = 0.1, c = 0.5, and Gr = Rab = Le = Sc = Pr = 1.0 |

|
| Fig. 7 Density of motile microorganism profile ξ(η) for various values of Sc with NT = Nr = NB = 0.1, c = 0.5, and Gr = Rab = Le = Pe = Pr = 1.0 and variation of various physical quantities with Nr in case of NT = NB = 0.1, c = 0.5, and Gr = Rab = Le = Pe = Pr = Sc = 1.0 |
It is well known that the physical quantities such as the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganism flux are of importance in practical applications. We therefore discuss their variation trends with various physical parameters successively.
As shown in Fig. 7(b),all of the four physical quantities reduce almost linearly as Nr evolves from 0 to 1. Among them,the local skin friction decays most rapidly,and the local wall motile microorganism flux lists in the second place. The local Nusselt number and the local wall mass flux have the least descendant rates. Physically,the difference of nanoparticle volumetric fraction between the wall and the ambient fluid can be the major factor to affect those changing trends. It is found from Fig. 8(a) that the variation of NT causes the different changing trends for those physical quantities. Its increase leads to the increase of the local skin friction,but results in the decrease of the local Nusselt number and the local wall mass flux. However,the variation of the local wall motile microorganism flux with NT is quite different. As NT enlarges, it decreases firstly and increases afterwards. It is plotted in Fig. 8(b) that NB has the effects on those quantities as well,the local skin friction enlarges slightly as it evolves. Similarly,the local wall mass flux and the local wall motile microorganism flux increase with NB. However, the local Nusselt number decreases as NB enlarges.

|
| Fig. 8 Variation of various physical quantities with NT in case of Nr = NB = 0.1, c = 0.5, and Gr = Rab = Le = Pe = Pr = 1.0 and with NB in case of Nr = NT = 0.1, c = 0.5, and Gr = Rab = Le = Pe = Pr = 1.0 |
In practice,the linear regression for those physical quantities can be important,which can be achieved by the linear regression analysis. For example,by setting Le = Gr = Pr = 1.0, NB = Nr = NT = 0.1,and c = 0.5,we are able to express them by the parameters Sc,Pe,and Rab in the following forms:
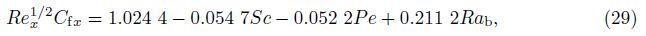
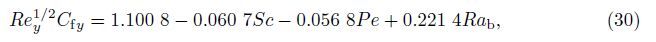
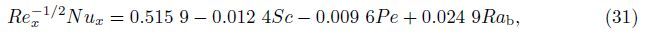
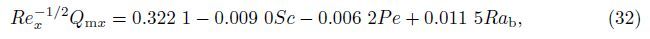
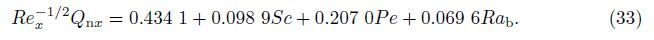
Similarly,we are able to give the linear regression of those quantities for the other physical parameters. For example,we define
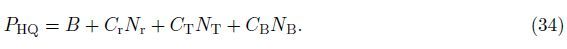
 |
 |
 |
 |
The free bio-convection flow in the stagnation of a three-dimensional body embedded in a nanofluid containing both nanoparticles and motile microorganisms is examined in detail. The very efficient HAM-FDM technique is proposed to give exact solutions for the reduced equations of the momentum,thermal energy,nanoparticles and motile microorganisms. The influence of various physical parameters such as the Brownian motion parameter and the thermophoresis parameter on the distribution of the motile microorganisms and the important physical quantities of practical interest including the local skin friction,the local Nusselt number,the local wall mass flux,and the local wall motile microorganism flux is presented and discussed.
In summary,the main contributions of this paper can be extracted as follows.
(i) The very efficient HAM-FDM technique is introduced,which can improve the computational efficiency to a large extent as compared with the traditional HAM technique.
(ii) The types of nanoparticle and the differences of nanoparticle volumetric fraction and/or temperature between the wall and the ambient fluid can significantly affect the distribution of microorganisms.
(iii) The body shape is a key factor to alter the density of the motile microorganisms. Moreover, the Prandtl number,the Lewis number,the bioconvection Rayleigh number,the Péclet number,and the Schmidt number can change the distribution of the motile microorganisms.
(iv) The linear regression formulae for physical quantities are given,which can be used in practical applications.
Appendix AIn view of the HAM technique,the solutions can be expressed by





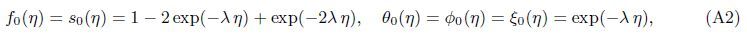





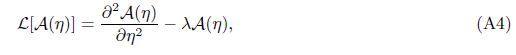
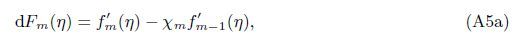
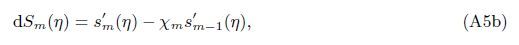
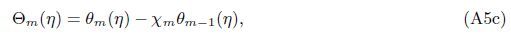
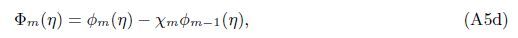
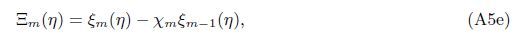
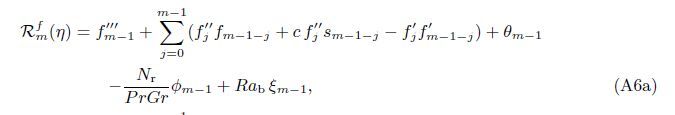
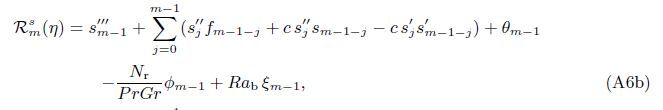
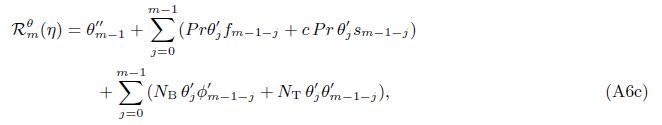
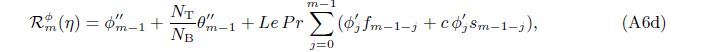
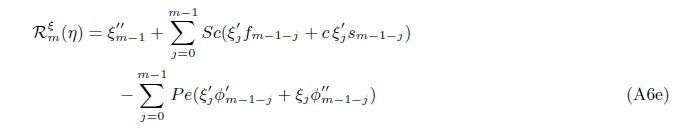

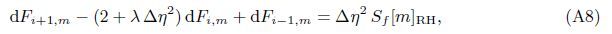
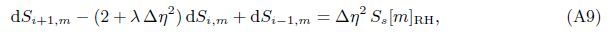
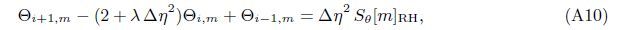
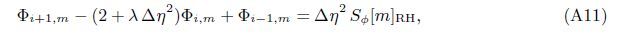
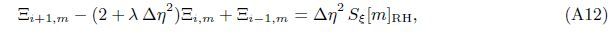
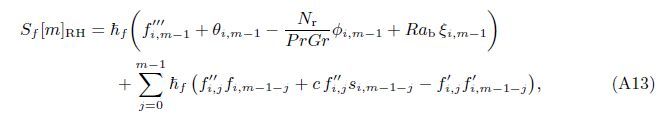
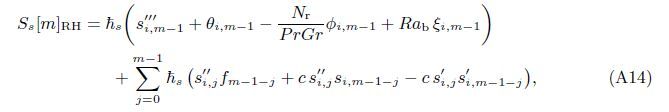
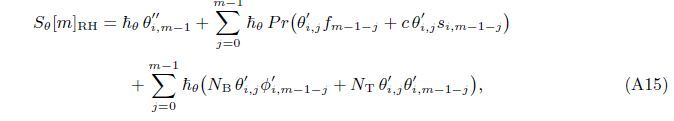
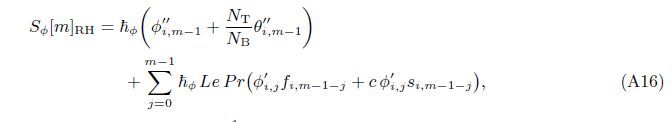
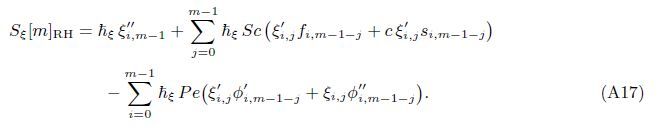
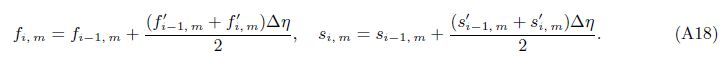
At the Mth order truncations,we can use the following iterative formulae to improve on the solution accuracies
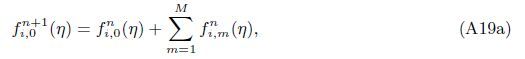
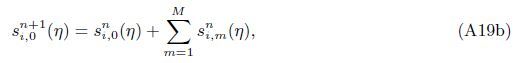
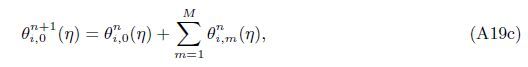
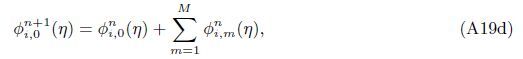
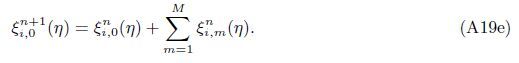
| [1] | Poots, G. Laminar free convection near the lower stagnation point on an isothermal curved surface. International Journal of Heat and Mass Transfer, 7(8), 863-874(1964) |
| [2] | Banks, W. H. H. Laminar free convection flow at a stagnation point of attachment on an isothermal surface. Journal of Engineering Mathematics, 8(1), 45-65(1974) |
| [3] | Ingham, D. B., Merkin, J. H., and Pop, I. Unsteady free convection of a stagnation point of attachment on an isothermal surface. International Journal of Mathematics and Mathematical Sciences, 7(3), 599-614(1984) |
| [4] | Pop, I. and Merkin, J. H. Three-dimensional Darcian free convection near a stagnation point on an isothermal surface. Transport in Porus Media, 2(4), 357-362(1987) |
| [5] | Slaouti, A., Takhar, H. S., and Nath, G. Unsteady free convection flow in the stagnation-point region of a three-dimensional body. International Journal of Heat and Mass Transfer, 41(22), 3397-3408(1998) |
| [6] | Xu, H., Liao, S. J., and Pop, I. Series solutions of unsteady free convection flow in the stagnationpoint region of a three-dimensional body. International Journal of Thermal Science, 47(5), 600-608(2008) |
| [7] | Zheng, L. C., Zhang, C. L., Zhang, X. X., and Zhang, J. H. Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. Journal of the Franklin Institute, 350(5), 990-1007(2013) |
| [8] | Zhang, C. L., Zheng, L. C., Zhang, X. X., and Chen, G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction. Applied Mathematical Modelling, 39, 165-181(2015) |
| [9] | Lin, Y. H., Zheng, L. C., Zhang, X. X., Ma, L. X., and Chen, G. MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. International Journal of Heat and Mass Transfer, 84, 903-911(2015) |
| [10] | Kuznetsov, A. V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. International Communications in Heat and Mass Transfer, 37(10), 1421-1425(2010) |
| [11] | Buongiorno, J. Convective transport in nanofluids. Journal of Heat Transfer, 128(3), 240-250(2006) |
| [12] | Kuznetsov, A. V. Nanofluid bio-thermal convection:simultaneous effects of gyrotactic and oxytactic micro-organisms. Fluid Dynamics Research, 43, 055505(2011) |
| [13] | Kuznetsov, A. V. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. European Journal of Mechanics-B/Fluids, 30(2), 156-165(2011) |
| [14] | Kuznetsov, A. V. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms:oscillatory instability. Nanoscale Research Letters, 6(1), 1-13(2011) |
| [15] | Kuznetsov, A. V. Nanofluid bioconvection:interaction of microorganisms oxytactic upswimming, nanoparticle distribution, and heating/cooling from below. Theoretical and Computational Fluid Dynamics, 26(1-4), 291-310(2012) |
| [16] | Tham, L., Nazar, R., and Pop, I. Mixed convection flow over a solid sphere embedded in a porous medium filled by a nanofluid containing gyrotactic microorganisms. International Journal of Heat and Mass Transfer, 62, 647-660(2013) |
| [17] | Xu, H. and Pop, I. Mixed convection flow of a nanofluid over a stretching surface with uniform free stream in the presence of both nanoparticles and gyrotactic microorganisms. International Journal of Heat and Mass Transfer, 75, 610-623(2014) |
| [18] | Kuznetsov, A. V. and Avramenko, A. A. Effect of small particles on the stability of bioconvection in a suspension of gyrotactic microorganisms in a layer of finite depth. International Communications in Heat and Mass Transfer, 31(1), 1-10(2004) |
| [19] | Geng, P. and Kuznetsov, A. V. Effect of small solid particles on the development of bioconvection plumes. International Communications in Heat and Mass Transfer, 31(5), 629-638(2004) |
| [20] | Geng, P. and Kuznetsov, A. V. Settling of bidispersed small solid particles in a dilute suspension containing gyrotactic micro-organisms. International Journal of Engineering Science, 43(11-12), 992-1010(2005) |
| [21] | Geng, P. and Kuznetsov, A. V. Introducing the concept of effective diffusivity to evaluate the effect of bioconvection on small solid particles. International Journal of Transport Phenomena, 7(2), 321-338(2005) |
| [22] | Liao, S. J. Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press, Beijing, 153-165(2012) |
 2016, Vol. 37
2016, Vol. 37


