1 Introduction

The studies on convective heat transfer have received great attention because of its wide applications in energy related engineering problems. Furthermore,a great number of investigations on nanofluid show that the nanoparticles in fluids can improve the thermal conductivity of these fluids. The studies on nanofluids have been reviewed by Eastman et al.^[1],Kakac and Pramaumjaroenkij^[2],and several others. These reviews discussed in detail the work done on convective transport in nanofluids. Boungiorno^[3] considered the different theories to explain the enhanced heat transfer characteristics of nanofluids. Kuznetsov and Neid^[4] studied the natural convective flow of a nanofluid over a vertical plate. In addition,they later extended the work to a nanofluid saturated porous medium^[5]. In Ref. ^[6],Makinde and Aziz investigated the boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Following these works,Ramesh and Gireesha^[7] considered the effects of heat source/sink on the steady boundary layer flow of a Maxwell fluid over a stretching sheet with the convective boundary condition in the presence of nanoparticles.

The boundary layer flow behaviors of non-Newtonian fluids have also attracted much interest due to the large number of practical applications in industrial and manufacturing processes. Because of the complexity of these fluids,there is not a single constitutive equation which exhibits all properties of such non-Newtonian fluids^{[8, 9, 10, 11, 12, 13]}. For example,some non-Newtonian fluid models cannot predict the effects of elasticity. However,the Maxwell model,a subclass of non-Newtonian fluids,which can predict the stress relaxation,has become more popular^{[14, 15]}. Noor^[16] presented analysis of the magnetohydrodynamic (MHD) flow of a Maxwell fluid past a vertical stretching sheet in the presence of thermophoresis and chemical reactions. Liu et al.^[17] studied the time periodic electroosmotic flow (EOF) of generalized Maxwell fluids between two microparallel plates and presented an analytical solution of EOF velocity. Hayat et al.^[18] obtained an analytic solution for the unsteady MHD flow in a rotating Maxwell fluid through a porous medium. Nadeem et al.^[19] analyzed the heat transfer of a Maxwell fluid past a stretching sheet.

Many of the above works have been done by the self-similar analysis theory. The classical method for finding similarity reduction of nonlinear differential equations is the Lie group method of infinitesimal transformations. It reduces the number of independent variables of the partial differential equations under consideration and keeps the system and associated initial and boundary condition invariant. A special form of Lie group transformations,known as the scaling group transformation,is the most powerful,sophisticated,and systematic method to generate similarity transform and is widely used in nonlinear dynamical systems,especially in the field of deterministic chaos^{[20, 21]} and different flow phenomena^{[22, 23, 24, 25, 26, 27, 28]}. For example,Asghar et al.^[22] discussed the steady three-dimensional flow and heat transfer of viscous fluid on a rotating disk stretching in the direction by radial Lie group theory symmetries. Abd-el-Malek et al.^[25] applied the Lie group method in studying nonlinear inviscid flows with a free surface under gravity. Hamad^[27] studied the effect of a magnetic field on the free convection flow of a nanofluid over a linear stretching by the scaling group of transformations.

Motivated by the above works,in this paper,we present a general procedure for applying the one-parameter group of transformations to the problem of the convection of a Maxwell fluid over a stretching porous surface with the heat source/sink in the presence of nanoparticles. As a result,we obtain the similarity transformation by the Lie group analysis. Furthermore, since most of the nanoparticle parameters are included in the temperature and concentration distribution equations,we discuss the effects of such physical parameters on the temperature and the concentration in detail.

2 Preliminaries

Consider a two-dimensional steady incompressible fluid flowing past a stretching porous surface with the convective boundary condition. In addition,the influence of heat source/sink and nanoparticle is considered,while the sheet is stretching from the plane $\bar y$ = 0. The flow is assumed to be confined to $\bar y$ > 0. Two equal and opposite forces are applied along the x-axis so that the sheet is stretched. The temperature of the sheet surface is the result of a convective heating process which is characterized by a temperature T_f and a heat transfer coefficient hf . Then,the boundary layer equations of Maxwell fluid along nanoparticles in the presence of heat source/sink are given as follows^[29]:

where ${\bar u}$ and ${\bar v}$ denote the velocities in the ${\bar x}$- and ${\bar y}$-directions,respectively,α is the thermal diffusivity,ρ_f is the base fluid density,ν is the fluid kinematic viscosity,T is the fluid temperature, T∞ is the ambient fluid temperature,κ₀ is the relaxation time of the upper convected Maxwell (UCM) fluid,Q₀ is the dimensional heat generation/absorption coefficient,D_B is the Brownian diffusion coefficient,D_T is the thermophoretic diffusion coefficient,c_p is the specific heat at the constant pressure,τ is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the ordinary fluid,and C is the nanoparticle volume fraction.

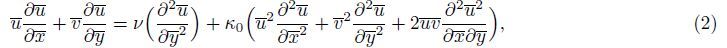
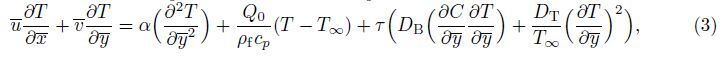
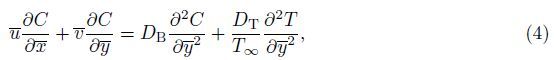
The appropriate boundary conditions for the physical problem are

where a > 0 is a constant,C_w is the fraction of nanoparticles at the wall,v_w is the wall velocity, κ is the effective thermal conductivity of nanofluid,and C_∞ is the ambient nanoparticle volume fraction.

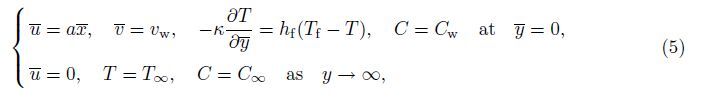
Introducing the following non-dimensional variables:

and the stream function Ψ defined by u =${{\partial \Psi } \over {\partial y}}$ and v =-${{\partial \Psi } \over {\partial x}}$ leads to the following nondimensional forms of (2)-(4): where β = aκ₀ (≥ 0) is the Maxwell parameter,S = ${{{Q_0}} \over {a{\rho _f}{c_p}}}$ is the heat source (S > 0) or sink (S < 0) parameter,N_B = ${{\tau {D_B}\left( {{C_w} - {C_\infty }} \right)} \over \nu }$ is the Brownian motion parameter,N_T = ${{\tau {D_T}\left( {{T_f} - {T_\infty }} \right)} \over {\nu {T_\infty }}}$ is the thermophoresis parameter,Le = ${\alpha \over {{D_B}}}$ is the Lewis number,and Pr = ${\nu \over \alpha }$ is the Prandtl number.The boundary conditions can be written as where M = - ${{{v_w}} \over {\sqrt {a\nu } }}$ is the permeability parameter (M > 0 corresponds to suction and M < 0 corresponds to blowing),and B_i = ${{{h_f}} \over \kappa }\sqrt {{\nu \over a}} $ is the Biot number.

3 Lie point symmetries and similarity solutions

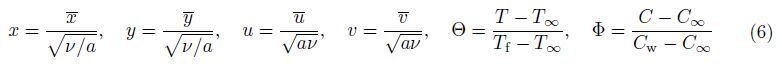
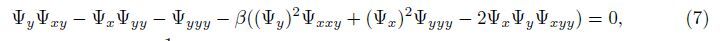
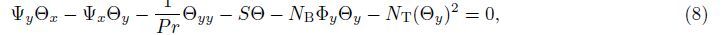
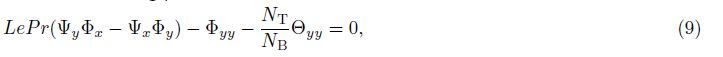
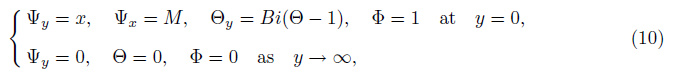
The symmetry groups of (7)-(9) are calculated using the classical Lie group approach. The one-parameter infinitesimal Lie group of transformations leaving (7)-(9) invariant is defined as

where the coordinates (x,y,Ψ,u,v,Θ,Φ) → (x^*,y^*,Ψ^*,u^*,v^*,Θ^*,Φ^*).

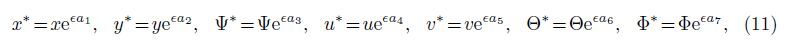
Substituting (11) into (7)-(9),we get

Since the system remains invariant under the group of transformations,we have a₁ = a₃ and a₂ = a₆ = a₇ = 0. Considering the boundary conditions,we obtain a₁ = a₃ = 1. Then,the characteristic equations for finding the similarity transformations are

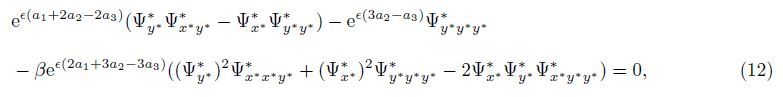
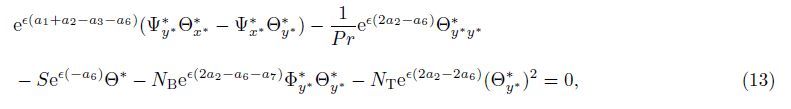
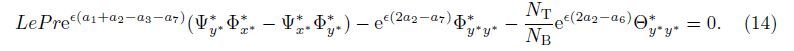
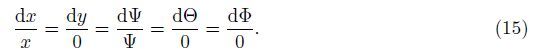
The corresponding similarity variable and functions are

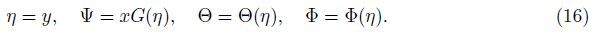
Substituting (16) into (7)-(9) yields the following ordinary equations:

The boundary conditions (10) become

4 Numerical solutions and discussion

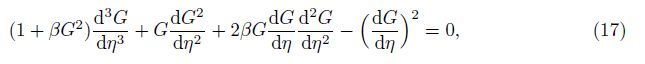
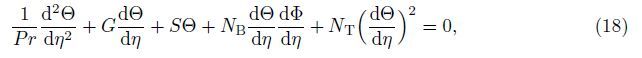
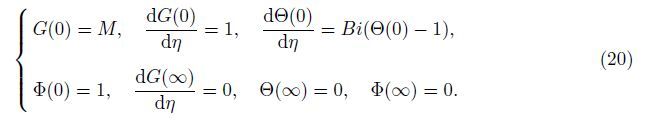
Since (17)-(19) together with the boundary conditions (20) are strongly nonlinear,a numerical treatment will be more appropriate. Thus,these equations are solved numerically by the Bvp₄c with MATLAB,and the results are presented graphically and in tables. During the process of numerical computation,the maximum residual error is defined to be less than 10^-6.

To test the accuracy of the applied numerical scheme,a comparison of the present results corresponding to -Θ'(0) and -Φ'(0) with those obtained by Makinde and Aziz^[6] is presented in Table 1,which shows a favorable agreement. Table 2 presents the numerical values of -Θ'(η) and -Φ'(η) at η = 0 for various values of the Prandtl number Pr,the heat source or sink parameter S,and the suction velocity M when the other parameters are fixed. We can find that both Θ'(0) and Φ'(0) are decreasing functions of the Prandtl number Pr.

In the following section,we focus on the effects of different parameters on the temperature and the concentration. To begin with,we discuss the effects of the Maxwell parameter β on the velocity G'(η). Figure 1 shows that G'(η) is an increasing function of the Maxwell parameter, and the boundary layer thickness increases with the increasing Maxwell parameter β when suction exists. Furthermore,the value of the velocity G'(η) decreases from 1 to zero as η changes from 0 to infinity.

Figure 2 gives the effects of the Biot number on the temperature and the concentration when there exists the heat source/sink. It can be observed that both the temperature and the concentration are increasing functions of the Biot number. Furthermore,the temperature considering the heat source is higher than that considering the heat sink,which agrees with the practical situation. We also find that the heat source or heat sink has little influence on the concentration.

Figure 3 shows the influence of the Lewis number on the temperature and concentration distributions. Both are decreasing functions of the Lewis number. We can find that the temperature distribution is considerably different when there exists the heat source/sink. When there exists the heat source,the temperature distribution is higher than that with the heat sink. However,when we consider the influence of the Lewis number on the concentration,the case is different. For the same Lewis number,the concentration with the heat sink is higher than that with the heat source. Furthermore,as the Prandtl number is smaller than 1,the boundary layer becomes thicker obviously not only for the temperature distribution but also for the concentration distribution. The similar phenomenon can also be found in Fig. 4.

Figure 4 exhibits the temperature and concentration distributions for several values of the Prandtl number. Both the temperature and concentration distributions are decreasing functions of the Prandtl number Pr and trend to zero as they are far away from the wall. However,for the fixed Prandtl number,the temperature with the heat source is higher than that with the heat sink.

Figure 5 illustrates the effects of the Brownian motion parameter on the temperature and the concentration. With the increase of the Brownian motion,the temperature also becomes high. Furthermore,the influence near the wall is obvious. However,it becomes small as the temperature is far away from the wall. When we consider the effect on the concentration,it is similar to the case of the Prandtl number.

Figures 6 and 7 show the effects of the thermophoresis parameter N_T and the suction velocity on the temperature and concentration distributions. Both the temperature and the concentration are increasing functions of the thermophoresis parameter. Furthermore,no matter there exists the heat source/sink,an extreme point appears near the wall when the thermophoresis parameter is large enough.

Figure 8 shows the influence of large heat source on the temperature distribution. According to the numerical solutions,a new phenomenon that is characterized by the oscillation of the temperature curves is found. This point needs to be explained in the future work.

5 Conclusions

Using group-theoretical methods,we obtain the similarity solutions of the convection of a Maxwell fluid over a stretching porous surface with the heat source/sink in the presence of nanoparticles. By determining the transformation group under which the given partial differential equation and its initial and boundary conditions are invariant,we obtain the invariants and the symmetries of this equation. In turn,by the help of these invariants and symmetries, we determine the similarity variables that reduce the number of independent variables. The influence of different physical parameters on the temperature or the concentration is different if we consider the heat source/sink. Furthermore,the suction velocity at the wall also has important influence on the velocity,temperature,and concentration distributions.