Shanghai University
Article Information
- S. E. AHMED, A. MAHDY. 2016.
- Laminar MHD natural convection of nanofluid containing gyrotactic microorganisms over vertical wavy surface saturated non-Darcian porous media
- Appl. Math. Mech. -Engl. Ed., 37(4): 471-484
- http://dx.doi.org/10.1007/s10483-016-2044-9
Article History
- Received May 28, 2015;
- in final form Sept. 11, 2015
| $\tilde a$amplitude of wavy surface; | Leb bioconvectionLewisnumber; |
| a,microorganisms concentration difference | Le,Lewis number; |
| parameter; | Mn,magnetic field parameter; |
| C,nanoparticle volume fraction; | N,rescaled density of motile microorgan |
| D,Brownian diffusion coefficient; | isms; |
| Dt,thermophoretic diffusion coefficient; | Nb,Brownian motion parameter; |
| Dn,diffusivity of microorganisms; | Nr,buoyancy ratio; |
| f,dimensionless stream function; | Nt,thermophoresis parameter; |
| g,acceleration due to gravity; | Nnx,local density number of motile microor |
| Gr,Grashofnumber; | ganisms; |
| k,thermal conductivity; | Nux,local Nusselt number; |
| K,permeability of porous medium; | P,pressure; |
| ${\bar K}$,material parameter; | Peb,bioconvectionPéclet number; |
| L,characteristic length of wavy surface; | qm,surface mass flux; |
| qn,surface motile microorganisms flux; | T,temperature; |
| qw,surface heat flux; | W,constant maximum cell swimming speed; |
| Ra,Rayleigh number; | (u,v),velocity components of fluid; |
| Rab,bioconvection Rayleigh number; | (x,y),coordinate axes. |
| Shx,local Sherwood number; |
| α,thermal diffusivity of porous media; | ρf ,density of fluid; |
| ϕ,dimensionless nanoparticle volume frac | ρp,nanoparticle mass density; |
| tion; | j,ratio between effective heat capacity of |
| β,volumetric expansion coefficient; | nanoparticle material and heat capacity |
| θ,dimensionless temperature; | of fluid; |
| (ξ,η),non-similarity variables; | μ,dynamic viscosity; |
| (ρc)p,effective heat capacity of nanoparticle | γ,average volume of microorganisms; |
| material; | σ,wavysurface; |
| (ρc)f ,heat capacity of fluid; | ψ,stream function. |
| w,condition at surface; | ∞,condition in free stream. |
| f,fluid; |
During the past several decades,the natural convection flow and heat transfer have received the attention of researchers owing to their many applications in mechanical,chemical,and civil engineering. These applications include,for example,fibrous insulation,food processing and storage,thermal insulation,geophysical systems,electrochemistry,metallurgy,the underground disposal of nuclear or non-nuclear waste,the cooling system of electronic devices,etc[1]. The books written by Nield and Bejan[2],Pop and Ingham[3],Ingham and Pop[4],Vafai[5, 6], and Vadasz[7] provide a good literature survey for this topic. In addition,the study of heat transfer near irregular surfaces is of fundamental importance because it is often found in many industrial applications. Many researchers are interested in the natural convection flow near the irregular surfaces saturated porous media. Cheng[8] studied the boundary layer flow and heat transfer near an inclined wavy plate in a bidisperse porous medium with the uniform wall temperature. The author found that the increase in the modified thermal conductivity ratio and the permeability ratio can enhance the natural convection heat transfer of the inclined plate in the bidisperse porous media. The problem of two-dimensional steady-state film condensation on an isothermal finite-size horizontal wavy plate embedded in a porous medium for the case in which the plate faces upward into a region of dry saturated vapor was investigated by Chang[9]. The results showed that the inclusion of capillary effects in the liquid film analysis has a significant effect on the computed results for the heat transfer coefficient. Elshehawey et al.[10] used the Brinkmain model to discuss the boundary layer flow of an incompressible viscous fluid moving through a porous medium between two inclined wavy porous plates under the effects of a constant inclined magnetic field that makes an angle with the vertical axis and constant suction/injection. Cheng[11] studied the effects of spatially wavy surface and fluid inertia on the natural convection heat and mass transfer near a vertical wavy surface embedded in a non-Darcy fluid-saturated porous medium. He observed that the rates of heat and mass transfer tend to decrease as the modified Grashof number increases,while the higher amplitudewavelength ratio decreases the average Nusselt and Sherwood numbers. Mahdy[12] studied the combined effect of spatially stationary surface waves and the presence of fluid inertia on the free convection along a heated vertical wavy surface embedded in an electrically conducting fluid saturated porous medium subject to the diffusion-thermo (Dufour),thermo-diffusion (Soret),and magnetic field effects. a very good review of convective heat transfer and fluid flow in porous media with nanofluid can be found from Mahdi et al.[13]. In this review,the porous media characteristics and properties of the nanofluids were mentioned in details. Moreover, studies on convective heat transfer and fluid flow in porous media with nanofluid were reported for the natural,forced,and mixed convection with different geometries containing the wavy case.
The macroscopic convection flow of fluid caused by the density gradient created by collective swimming of motile microorganisms is known as the bioconvection flow. These self-propelled motile microorganisms increase the density of the base fluid by swimming in a particular direction, thus causing bioconvection. Khan et al.[14] used the Oberbeck-Boussinesq approximation and similarity transformation to study the magnetohydrodynamic (MHD) boundary layer flow, heat and mass transfer of a water-based nanofluid containing gyrotactic microorganisms over a vertical plate in the presence of the Navier slip effect. They found that the magnetic,buoyancy, nanofluid,and bioconvection parameters reduce the Nusselt,Sherwood,and density numbers of microorganisms. Xu and Pop[15] discussed analytically the mixed convection flow and heat transfer over a stretching surface with uniform free stream in the presence of both nanoparticles and gyrotactic microorganisms. Their results showed that the local Nusselt number reduces almost linearly as the thermophoresis parameter increases. The onset of bioconvection in a horizontal layer filled with a nanofluid that also contains gyrotactic microorganisms was presented by Kuznetsov[16]. a linear instability analysis and a Galerkin method were used to obtain an analytical solution for the critical Rayleigh number for the non-oscillatory situation. Xu and Pop[17] used the model proposed by Kuznetsov and Nield[18] to discuss the mixed bioconvection flow in a horizontal channel filled with a nanofluid that contains both nanoparticles and gyrotactic microorganisms. They observed that the increase of the Lewis number and the thermophoresis parameter helps to enhance the temperature distributions for the positive Reynolds numbers,but it results in the decrease of temperature profiles for the negative Reynolds number. Mahdy[19] studied the same problem for a vertical cone in porous media,where bioconvection takes place in a peristaltic flow in an asymmetric channel filled by nanofluid containing gyrotactic microorganism. The bio-nano-engineering model was reported by Akbar[20]. Moreover, Raees et al.[21] presented the case of mixed convection in gravity-driven nano-liquid film containing both nanoparticles and gyrotactic microorganisms. An excellent review for the current problem can be found in Refs. [22, 23, 24, 25],in which the cases of the stretching sheet,the square porous cavity,the non-Newtonian nanofluids in porous media,and a permeable vertical plate, were presented,respectively. More studies can be found in Refs. [26, 27, 28, 29].
Mahdy and Ahmed[30] performed a numerical analysis to examine laminar free convective of a nanofluid along a vertical wavy surface saturated porous medium. They found that the heat and mass transfer rates decrease by increasing either the buoyancy ratio number or the thermophoresis parameter. However,they neglected the effects of inertia as well as the presence of both nanoparticles and gyrotactic microorganisms. Therefore,the main objective of the present study is to investigate the MHD boundary layer flow and heat transfer over a vertical wavy surface saturated isotropic porous medium in the presence of both nanoparticles and gyrotactic microorganisms. The partial differential equations governing the problem are,firstly, transformed into a vertical flat plate,and the non-similar solutions are used to solve the resulting system. The obtained numerical results are presented in terms of the local Nusselt number,the local Sherwood number,the local density number of the motile microorganisms,the velocity profiles,the temperature distributions,and the rescaled density of the motile microorganisms.
2 Problem analysisLet us consider a two-dimensional steady free convection boundary layer flow over a vertical wavy plate placed in a non-Darcian nanofluid saturated porous medium containing gyrotactic microorganisms subject to a magnetic field. The coordinate system is chosen such that the ${\tilde x}$-axis is along the wavy surface whereas the ${\tilde y}$-axis is normal outward,as shown in Fig. 1. The wavy surface profile is chosen to be


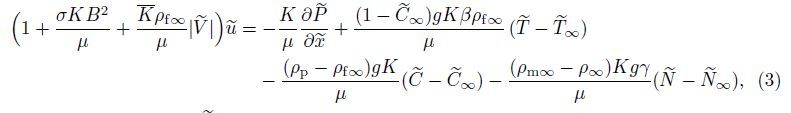

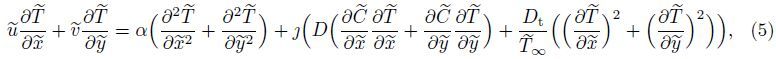
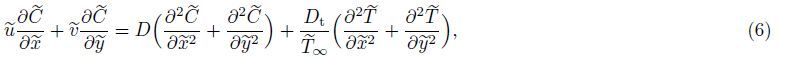
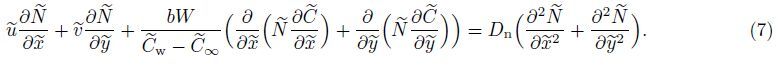

|
| Fig. 1 Schematic view and utilized coordinate system |
In the previous equations,${\tilde u}$ and ${\tilde v}$ are the velocity components along the ${\tilde x}$- and ${\tilde y}$-axes,μ is the dynamic viscosity of the fluid,α and β are the thermal diffusivity and the volumetric expansion coefficient,respectively,ρf is the density of the base fluid,ρp is the density of nanoparticles, ρm∞ is the microorganism density,and γ is the average volume of microorganisms. W is the constant maximum cell swimming speed,D,Dt,and Dn are the Brownian,thermophoretic diffusion,and diffusivity of microorganisms coefficients,respectively,and j = ∈(ρc)p/(ρc)f is the ratio of the effective heat capacity of the nanoparticle material to the heat capacity of the fluid. It is clear that the case of Darcy law is recovered when ${\bar K}$ = 0. K is the permeability of the porous medium,and ${\bar K}$ is a material parameter which may be thought of as a measure of the inertial impedance of the matrix. ${\tilde V}$ = (${\tilde u}$,${\tilde v}$) is the velocity flux vector. In addition,both the permeability K and the material parameter ${\bar K}$ can be determined from the widely-known correlations proposed by Ergun’s relations[31],
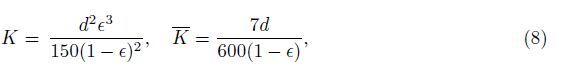
Now,the dimensional boundary conditions for the problem are
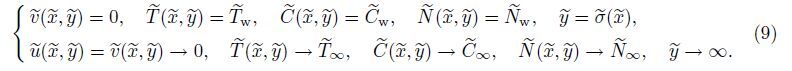
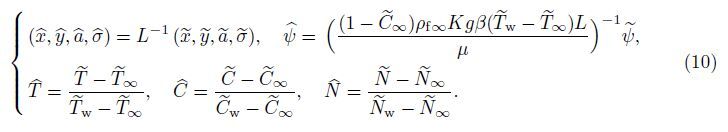
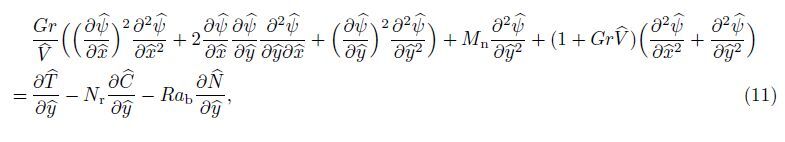
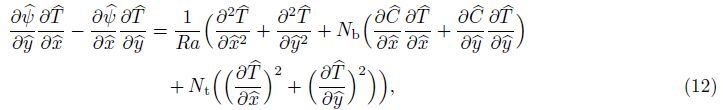
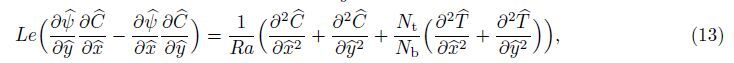
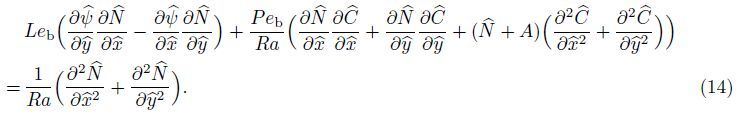
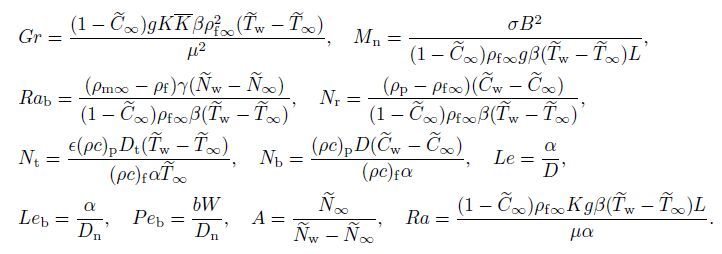
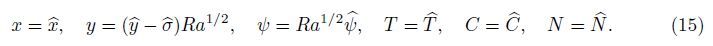
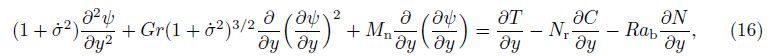
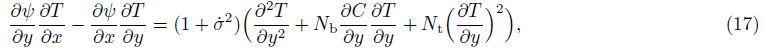
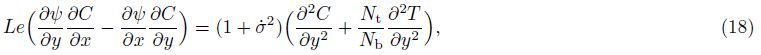
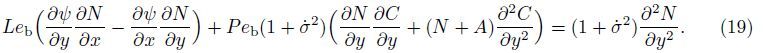
Now,Eqs. (16)-(19) may be reduced to a form more convenient for the numerical solution by considering the following transformations:
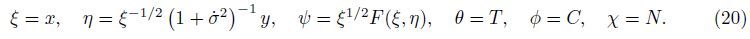
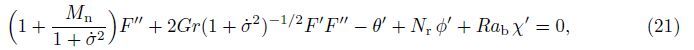
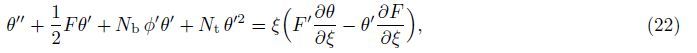
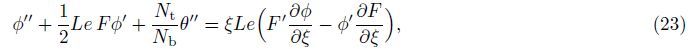
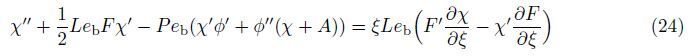
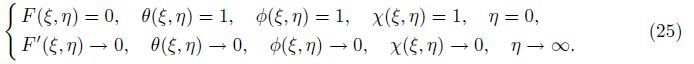
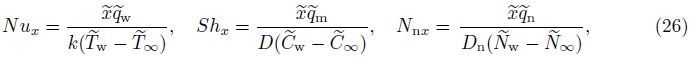
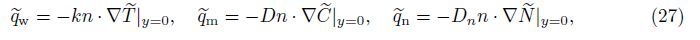
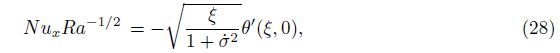
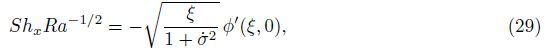
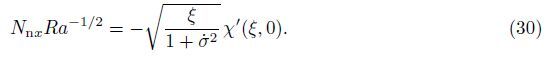
In this section,the governing equations (21)-(24) together with the boundary conditions (25) are solved numerically using the fourth-order Runge-Kutta method. In this technique, the solutions are divided to steps,namely,the first level of truncation and the second level truncation. For the first level of truncation,the derivatives with respect to ξ in Eqs. (21)-(24) are neglected. Thus,Eqs. (21)-(24) can be written as
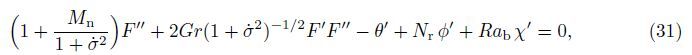


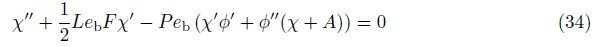
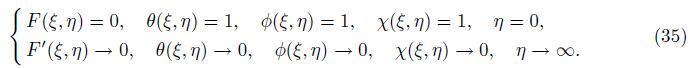
In the second step,all the neglected terms in the first truncation level are restored,and the following new variables are introduced:
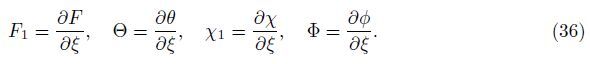
Thus,the governing equations are
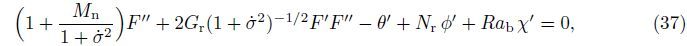
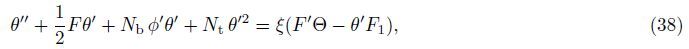
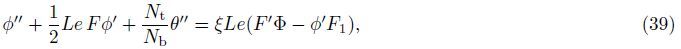
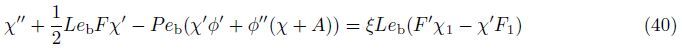
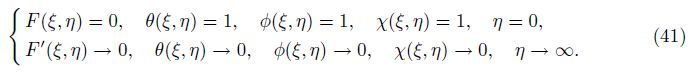
 |
The obtained results are presented in terms of the local Nusselt number,the local Sherwood number,and the local density number of the motile microorganisms for wide ranges of the governing parameter. In the presented study,the Grashof number Gr is considered to vary from 0 to 10,the magnetic field parameterMnvaries from 0 to 5,the thermophoresis parameter Nt varies from 0.1 to 1.2,the Brownian motion parameter Nb varies from 0.5 to 1.0,the buoyancy ratio varies from 0.1 to 0.4,and the bioconvection Rayleigh number varies from 0 to 0.4.
Figures 2-4 show the effect of the Grashof number Gr on the local Nusselt Nux,the local Sherwood number Shx,and the local density number of the motile microorganisms Nnx, respectively,for different values of the bioconvection Rayleigh number Rab. It is observed that the increase in the Grashof number Gr causes a reduction in the profiles of Nux,Shx, and Nnx. This is due to the fact that the increase in Gr reduces the dimensionless velocity and increases the dimensionless temperature,the dimensionless concentration,and the rescaled density of motile microorganisms within the boundary layer and consequently decreases Nux, Shx,and Nnx. In addition,an increase in the bioconvection Rayleigh number Rab results in a clear reduction in the thermal boundary layer thickness,the concentration boundary layer thickness,and the motile microorganisms boundary layer thickness,and as a result,Nux,Shx, and Nnx decrease as Rab increases. This is due to the fact that Rab reduces the dimensionless velocity and increases the dimensionless temperature,the dimensionless concentration,and the dimensionless rescaled density of motile microorganisms,and as a result,Nux,Shx,and Nnx decrease with an increase in the bioconvection Rayleigh number.

|
| Fig. 2 Effect of Grashof number on profiles of local Nusselt number for different values of bioconvection Rayleigh number |

|
| Fig. 3 Effect of Grashof number on profiles of local Sherwood number for different values of bioconvection Rayleigh number |

|
| Fig. 4 Effect of Grashof number on profiles of local density number of motile microorganisms for different values of bioconvection Rayleigh number |
The effects of the magnetic field parameterMnon the local Nusselt number Nux,the local Sherwood number Shx,and the local density number of the motile microorganisms Nnx are displayed in Figs. 5-7,respectively. The results show that asMnincreases,Nux,Shx,and Nnx increase. The reason for these behaviors is due to an additional resistance induced by the magnetic field that increases the thermal boundary layer thickness and consequently increases Nux,Shx,and Nnx.

|
| Fig. 5 Effect of magnetic field parameter on profiles of local Nusselt number for different values of bioconvection Rayleigh number |

|
| Fig. 6 Effect of magnetic field parameter on profiles of local Sherwood number for different values of bioconvection Rayleigh number |

|
| Fig. 7 Effect of magnetic field parameter on profiles of local density number of motile microorganisms for different values of bioconvection Rayleigh number |
Figure 8 shows the effect of the thermophoresis parameter on the profiles of the local Nusselt number for different values of the bioconvection Rayleigh number. The figure shows a clear reduction in the local Nusselt number obtained by increasing Nt. This can be attributed to the temperature difference in the boundary layer region which increases by increasing Nt that leads to increasing the temperature distributions and decreasing the thermal boundary layer thickness. On the contrary,the increase in Nt results in an increase in the local Sherwood number and the local density number of the motile microorganisms. This behavior can be noted from Figs. 9 and 10 which display the effects of Nt on Shx and Nnx.

|
| Fig. 8 Effect of thermophoresis parameter on profiles of local Nusselt number for different values of bioconvection Rayleigh number |

|
| Fig. 9 Effect of thermophoresis parameter on profiles of local Sherwood number for different values of bioconvection Rayleigh number |

|
| Fig. 10 Effect of thermophoresis parameter on profiles of local density number of motile microorganisms for different values of bioconvection Rayleigh number |
Figure 11 depicts the effect of the Brownian motion parameter on the profiles of the local Nusselt number for different values of the bioconvection Rayleigh number. It is clear that Nux takes the higher values at small values of Nb. The reason for that is due to the viscosity of the nanofluid that increases as Nb increases which in turn decreases the velocity profiles and decreases the thermal boundary layer thickness. Figure 12 andFigure 13 show the opposite behavior for the local Sherwood number Shx and the local density number of the motile microorganisms Nnx. As it can be seen from these figures,the increase in Nb results in an increase in the concentration boundary layer thickness and the rescaled density of motile microorganisms boundary layer thickness that increases Shx and Nnx.

|
| Fig. 11 Effect of Brownian motion parameter on profiles of local Nusselt number for different values of bioconvection Rayleigh number |

|
| Fig. 12 Effect of Brownian motion parameter on profiles of local Sherwood number for different values of bioconvection Rayleigh number |

|
| Fig. 13 Effect of Brownian motion parameter on profiles of local density number of motile microorganisms for different values of bioconvection Rayleigh number |
Figures 14-16 display the profiles of the local Nusselt number Nux,the local Sherwood number Shx,and the local density number of the motile microorganisms Nnx under the effect of the buoyancy ratio Nr. Like the effect of Gr,the increase in Nr causes a significantly reduction in Nux,Shx,and Nnx. In fact,the increase in Nr declares the fluid motion which increases the temperature distributions,the concentration distribution,and the distributions of the rescaled density of motile microorganisms,and as a result,the gradients of temperature, concentration,and rescaled density of motile microorganisms decrease. Consequently,Nux, Shx,and Nnx decrease. All these behaviors are presented with the referenced case of Mn = 1, a = 0.2,Le = 6,Nr = 0.3,Nt = Nb = 0.6,Leb = 5,Peb = 0.4,Rab = 0.3,and a = 0.1.

|
| Fig. 14 Effect of buoyancy ratio on profiles of local Nusselt number for different values of bioconvection Rayleigh number |

|
| Fig. 15 Effect of buoyancy ratio on profiles of local Sherwood number for different values of bioconvection Rayleigh number |

|
| Fig. 16 Effect of buoyancy ratio on profiles of local density number of motile microorganisms for different values of bioconvection Rayleigh number |
The problem of laminar MHD non-Darcian free convection from a vertical wavy surface in porous media saturated by nanofluid containing gyrotactic microorganisms is investigated in the current paper. a non-similar solution and the fourth-order Runge-Kutta method are used to solve the partial differential equations governing the problem. It is found that the increase in the Grashof number reduces the local Nusselt number,the local Sherwood number, and the local density number of the motile microorganisms. In addition,as the magnetic field parameter increases,the local Nusselt number,the local Sherwood number,and the local density number of the motile microorganisms decrease. The increase in the bioconvection parameter leads to decreasing the dimensionless velocity,the local Nusselt number,the local Sherwood number,and the local density number of the motile microorganisms. a clear reduction in the local Nusselt number is obtained by increasing the thermophoresis parameter or the Brownian motion parameter,while the local Sherwood number and the local density number of the motile microorganisms increase by increasing the thermophoresis parameter or the Brownian motion parameter. As the buoyancy ratio increases,the local Nusselt number,the local Sherwood number,and the local density number of the motile microorganisms decrease.
| [1] | Aziz, A., Khan, W. A., and Pop, I. Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic microorganisms. International Journal of Thermal Sciences, 56, 48-57(2012) |
| [2] | Nield, D. A. and Bejan, A. Convection in Porous Media, 3rd ed., Springer, New York (2006) |
| [3] | Pop, I. and Ingham, D. B. Convective Heat Transfer:Mathematical and Computational Modeling of Viscous Fluids and Porous Media, Pergamon, Oxford (2001) |
| [4] | Ingham, D. B. and Pop, I. Transport Phenomena in Porous Media III, Elsevier, Oxford (2005) |
| [5] | Vafai, K. Handbook of Porous Media, 2nd ed., Taylor & Francis, New York (2005) |
| [6] | Vafai, K. Porous Media:Applications in Biological Systems and Biotechnology, CRC Press, Boca Raton (2010) |
| [7] | Vadasz, P. Emerging Topics in Heat and Mass Transfer in Porous Media, Springer, New York (2008) |
| [8] | Cheng, C, Y. Natural convection heat transfer from an inclined wavy plate in a bidisperse porous medium. International Communications in Heat and Mass Transfer, 43, 69-74(2013) |
| [9] | Chang, T. Laminar film condensation on a horizontal wavy plate embedded in a porous medium. International Journal of Thermal Sciences, 47, 35-42(2008) |
| [10] | Elshehawey, E. F., Elbarbary, E. M. E., and Elgazery, N. S. Effect of inclined magnetic field on magneto fluid flow through a porous medium between two inclined wavy porous plates (numerical study). Applied Mathematics and Computation, 135, 85-103(2003) |
| [11] | Cheng, C. Y. Non-Darcy natural convection heat and mass transfer from a vertical wavy surface in saturated porous media. Applied Mathematics and Computation, 182, 1488-1500(2006) |
| [12] | Mahdy, A. MHD non-Darcian free convection from a vertical wavy surface embedded in porous media in the presence of Soret and Dufour effect. International Communications in Heat and Mass Transfer, 36, 1067-1074(2009) |
| [13] | Mahdi, R. A., Mohammed, H. A., Munisamy, K. M., and Saeid, N. H. Review of convection heat transfer and fluid flow in porous media with nanofluid. Renewable and Sustainable Energy Reviews, 41, 715-734(2015) |
| [14] | Khan,W. A., Makinde, O. D., and Khan, Z. H. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. International Journal of Heat and Mass Transfer, 74, 285-291(2014) |
| [15] | Xu, H. and Pop, I. Mixed convection flow of a nanofluid over a stretching surface with uniform free stream in the presence of both nanoparticle and gyrotactic microorganisms. International Journal of Heat and Mass Transfer, 75, 610-623(2014) |
| [16] | Kuznetsov, A. V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. International Communications in Heat and Mass Transfer, 37, 1421-1425(2010) |
| [17] | Xu, H. and Pop, I. Fully developed mixed convection flow in a horizontal channel filled by a nanofluid containing both nanoparticles and gyrotactic microorganisms. European Journal of Mechanics-B/Fluids, 46, 37-45(2014) |
| [18] | Kuznetsov, A. V. and Nield, D. A. The Cheng-Minkowycz problem for natural convective boundary layer flow in a porous medium saturated by a nanofluid a revised model. International Journal of Heat and Mass Transfer, 65, 682-685(2013) |
| [19] | Mahdy, A. Natural convection boundary layer flow due to gyrotactic microorganisms about a vertical cone in porous media saturated by a nanofluid. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 38, 67-76(2015) |
| [20] | Akbar, N. S. Bioconvection peristaltic flow in an asymmetric channel filled by nanofluid containing gyrotactic microorganism:bio nano engineering model. International Journal of Numerical Methods for Heat and Fluid Flow, 25, 214-224(2015) |
| [21] | Raees, A., Xu, H., Sun, Q., and Pop, I. Mixed convection in gravity-driven nano-liquid film containing both nanoparticles and gyrotactic microorganisms. Applied Mathematics and Mechanics (English Edition), 36(2), 163-178(2015) DOI 10.1007/s10483-015-1901-7 |
| [22] | Khan, W. A. and Makinde, O. D. MHD nanofluid bioconvection due to gyrotactic microorganisms over a convectively heat stretching sheet. International Journal of Thermal Sciences, 81, 118-124(2014) |
| [23] | Sheremet, M. A. and Pop, I. Thermo-bioconvection in a square porous cavity filled by oxytactic microorganisms. Transport in Porous Media, 103, 191-205(2014) |
| [24] | Uddin, M. J., Khan, W. A., and Ismail, A. I. M. Free convective flow of non-Newtonian nanofluids in porous media with gyrotactic microorganism. Journal of Thermophysics and Heat Transfer, 27, 326-333(2013) |
| [25] | Mutuku, W. N. and Makinde, O. D. Hydromagnetic bioconvection of nanofluid over a permeable vertical plate due to gyrotactic microorganisms. Computers and Fluids, 95, 88-97(2014) |
| [26] | Hillesdon, A. J. and Pedley, T. J. Bioconvection in suspensions of oxytactic bacteria:linear theory. Journal of Fluid Mechanics, 324, 223-259(1996) |
| [27] | Hill, N. A., Pedley, T. J., and Kessler, J. O. Growth of bioconvection patterns in a suspension of gyrotactic microorganisms in a layer of finite depth. Journal of Fluid Mechanics, 208, 509-543(1989) |
| [28] | Kuznetsov, A. V. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. European Journal of Mechanics-B/Fluids, 30, 156-165(2011) |
| [29] | Makinde, O. D. Computational modeling of MHD unsteady flow and heat transfer over a flat plate with Navier slip and Newtonian heating. Brazilian Journal of Chemical Engineering, 29, 159-166(2012) |
| [30] | Mahdy, A. and Ahmed, S. E. Laminar free convection over a vertical wavy surface embedded in a porous medium saturated with a nanofluid. Transport in Porous Media, 91, 423-435(2012) |
| [31] | Ergun, S. Fluid flow through packed columns. Chemical Engineering Progress, 48, 89-94(1952) |
| [32] | Mahdy, A. and Ahmed, S. E. Thermosolutal Marangoni boundary layer magnetohydrodynamic flow with the Soret and Dufour effects past a vertical flat plate. Engineering Science and Technology, an International Journal, 18, 24-31(2015) |
| [33] | Nield, D. A. and Kuznetsov, A. V. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer, 52, 5792-5795(2009) |
 2016, Vol. 37
2016, Vol. 37


