Shanghai University
Article Information
- Bensong YU, Dongping JIN, Hao WEN. 2016.
- Nonlinear dynamics of flexible tethered satellite system subject to space environment
- Appl. Math. Mech. -Engl. Ed., 37(4): 485-500
- http://dx.doi.org/10.1007/s10483-016-2049-9
Article History
- Received May 24, 2015;
- in final form Nov. 4, 2015
A tethered satellite system during station-keeping phase is commonly subjected to the perturbations from space environments,such as the J2 perturbation,the air drag force,the solar pressure,the heating effect,and the orbital eccentricity,resulting in oscillations around a local equilibrium position of the system[1, 2, 3, 4, 5].
A considerable number of studies on the dynamics of tethered satellite systems have indicated the important nonlinear features,including bifurcations,quasi-periodic oscillations,and chaotic motions. For example,Steiner[6] pointed out that transient chaotic motions would occur in the vicinity of a saddle point of system. Nakanishi and Fujii[7] studied the attitude motion of a tethered satellite system in terms of the bifurcation analysis,the Lyapunov exponents,and the Poincar´e map,in which the elasticity of tether was ignored. Using a dumbbell model in elliptic orbits,Nakanishi et al.[8] found that the periodic motion diverges as the eccentricity increases and becomes chaotic in the neighborhood of eccentricity e = 0.313 8. Based on the elastic tether’s model,Mankala and Agrawal[9] investigated the deployment/retrieval dynamics of tethered satellite systems. Ellis and Hall[10] developed a nonlinear model of the two-point masses connected by a rigid rod,and focused on the nonlinear characteristics of out-of-plane librations. By the one-dimensional continuum model of tether,Yu and Jin[11] analyzed the effect of space environments on the dynamics of a tethered sub-satellite of being deployed and retrieved. With the help of a rigid-rod model of tether,Kojima et al.[12] established a groundbased apparatus to study the in-plane periodic motions of a tethered satellite system in elliptic orbits and carried out numerical simulations to test the validity of the derived equations of motion. Zhang et al.[13] presented a criterion for the existence of periodic motions of a tethered satellite system,according to the coincidence degree theory. Based on Kane’s method,Jin et al.[14] investigated the quasi-periodic motion of a tethered sub-satellite via the ground-based experimental system. Zhong and Zhu[15] studied the libration dynamics and stability of a short and bare electrodynamic tether for deorbiting nano-satellites subjected to space environmental perturbations. In addition,Avanzini and Fedi[16, 17] studied the dynamics of multi-tethered satellite formations. The results indicated that the tether mass and the orbit eccentricity affect the formation dynamics.
Actually,space tethers connecting satellites are of elasticity and have little rigidness to resist the bending or torsion. To get better insight into the dynamics of tethered satellite systems,it is better to consider the tethers as elastic ones rather than rigid rods. To the authors’ knowledge, however,the most of the published works on nonlinear dynamics are based on the simplified rigid-rod or inelastic tether model,in which the important space environments are ignored.
This paper pays attention to the nonlinear dynamics of a flexible tethered satellite system subject to space environments,including the J2 perturbation,the air drag force,the solar pressure,the heating effect,and the orbital eccentricity. The study,begins with establishing the nonlinear dynamic model of the flexible tethered satellite system in Section 2,and then in Section 3,based on the simplified linear-elastic model,gives the stability analysis of the system in an orbital reference frame. Finally,in Section 4,cases are studied numerically,including the equilibrium positions and the effects of space environments on nonlinear dynamics.
2 Mechanics modelConsider a tethered satellite system in the station-keeping phase,as shown in Fig. 1. The tethered satellite system consists of a mother satellite M with the mass mM and a sub-satellite S with the mass mS. The two satellites are connected by a viscoelastic tether wound on the spool of deployment device in the satellites. The unstrained length of the tether is l,Young’s modulus is E,the cross-sectional area is A,and the linear mass density is ρ. An inertial frame of reference O-XYZ is established such that the X-axis points towards the direction of ascending node from the center of the Earth O,the Z-axis is perpendicular to the orbital plane of the tethered satellite system that is marked by dashed lines in the figure,and the Y -axis is determined by the right-hand rule. An orbital frame O-xyz is on the center of the mother satellite,where the y-axis points towards the zenith,the z-axis is parallel to the Z-axis,and the x-axis is given by the right-hand rule. In Fig. 1,δ represents the angle of inclination between the orbital plane and the equatorial plane,and γ is the angle measured from the X-axis to the Sun’s rays. The so-called pitch angle θ is defined as the angle from OM to SM as indicated in the figure.

|
| Fig. 1 Schematic view of flexible tethered satellite system |
The viscoelastic tether is divided into n uniform elements with the lumped mass me = ρle located at the center of each element,where le = l/n denotes the standard length of a tether element,i.e.,the initial length between the two adjacent lumped masses,as shown in Fig. 2. The standard length of tether element will be invariable if the initial temperature Tst keeps constant. For convenience,let us mark the mother satellite M with node 0,the lumped masses of tether elements with nodes 1,2,· · · ,n numbered orderly from the mother satellite to the sub-satellite,and the sub-satellite S with node n + 1. Apparently,by taking a large enough number of elements,we will get a good approximation for the continuum system. From the Newton’s laws,we obtain the dynamic equation of the ith node as follows:

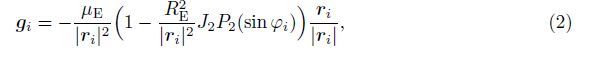
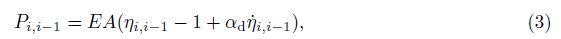

|
| Fig. 2 Lumped mass model of system |
The temperature of tether is mostly caused by the solar radiation,the infrared radiation of the Earth,and the infrared radiation of tether[18]. When a tether segment faces the Sun,the thermal power of the solar radiation on the tether segment becomes
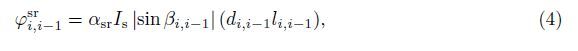
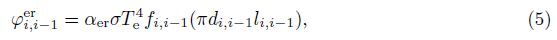
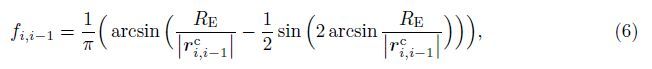
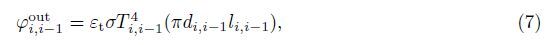
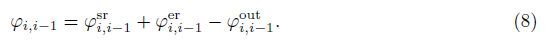


The resultant external forces acting on the tethered satellite system are the air drag force and the solar pressure. The air drag force can be written as

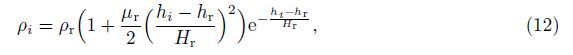
It is easy to write out the solar pressure acting on the tether segment facing the Sun,i.e.,
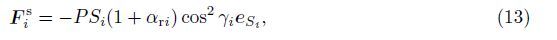
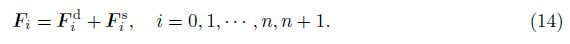
A simplified linear-elastic model is adopted to analyze the stability of high-dimensional nonlinear systems. The tether is envisioned as a linear-elastic one without consideration of its mass. The origin of orbital reference frame is set at the center of the mother satellite. The dynamical equations of motion can be expressed in the forms of
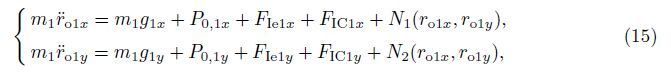
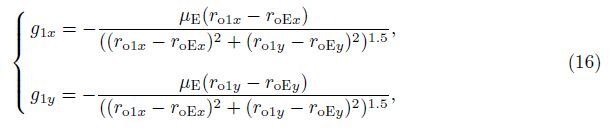
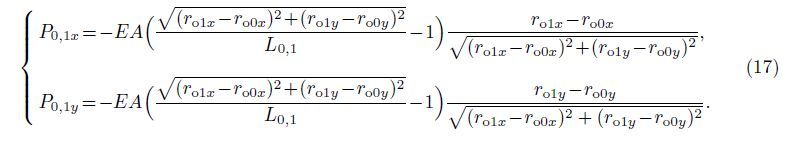
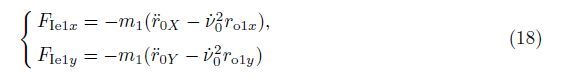

With q1 = ro1x,q2 = ˙ro1x,q3 = ro1y,and q4 = ${\dot r}$o1y,(15) can be recast as a set of state equations as follows:
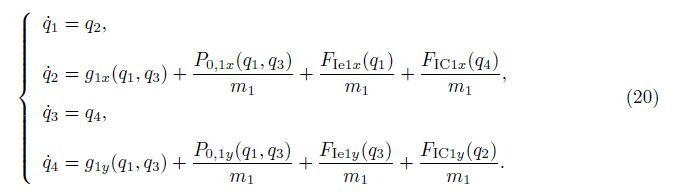
The Jacobian matrix of (20) is
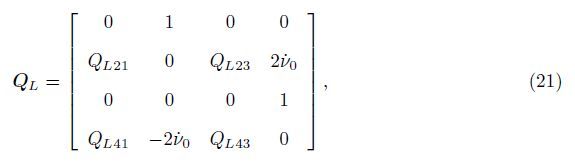
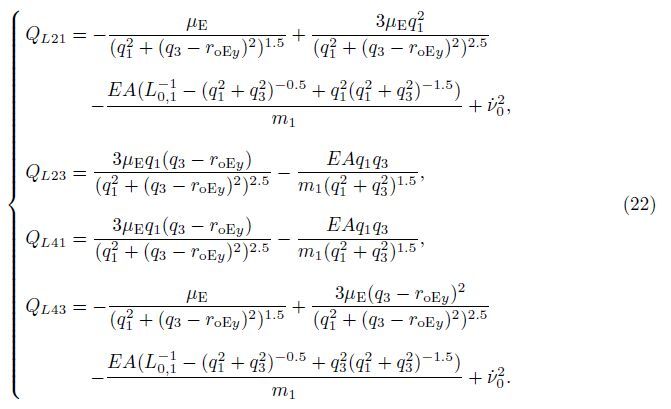
One can see that there exist four equilibrium positions in the tethered satellite system[6],of which the stability can be analyzed by the eigenvalues of the Jacobian matrix.
4 Case studiesTo study the stability of the equilibrium positions and the nonlinear dynamics of the tethered satellite system during the station-keeping phase,a set of parameters is taken as follows. The masses of the mother satellite and the sub-satellite are set as mM = 1 000 × 103 kg and mS = 1 × 103 kg,respectively. Young’s modulus of the tether is E = 50 GPa,and the crosssectional area is A = 10-6 m2. The linear mass density of the tether is ρ = 5×10-3 kg/m,and the length is l=10 km with n = 20. The dissipation constant of the tether is set as αc = 0.05. The argument of perigee is ω = π/2. Let the mother satellite be at the perigee position so that the initial true anomaly becomes ν0 = 0.
An ideal case without any perturbations of space environments is taken to check the numerical procedure first. Assume that the mother satellite moves in an in-plane circular orbit of 350 km away from the Earth. The in-plane pitch oscillations in the orbital frame O-xyz within two orbital periods of 10 980 s are obtained,as shown in Fig. 3. One can see from Fig. 3 that the simulation results show an acceptable calculation precision and the free oscillation feature for the viscoelastic tethered satellite system. In short,if a tethered satellite system moves in a circular orbit and lies initially in its local equilibrium,the equilibrium will remain unchanged until a space perturbation acts. The free oscillation of sub-satellite caused by an initial pitch angular velocity of ${\dot \theta }$0 = 5 × 10-5 rad/s is shown in Fig. 4. Figure 4(a) plots the trajectory of the sub-satellite,which is similar to that of a spring-mass pendulum. According to the spring-mass pendulum model,the period of the lateral oscillation can be obtained analytically as Tp = 2π/ $\sqrt {\mu \left( {r_{n + 1}^{ - 3} - r_0^{ - 3}} \right){r_0}/{l_{0,n + 1}}} $ 1. The analytical solution of the period is 3 164.3 s. The numerical result of the period is 3 167.3 s by setting x = l0,n+1 sin θ,as shown in Fig. 4(b). One can see that the analytical and numerical results coincide with each other. Figures 4(c) and 4(d) express the longitudinal oscillation of sub-satellite and its zoom view. The periodic oscillation of the sub-satellite has a period of about 89.7 s,which approaches that obtained from the analytical expression,88.9 s,in terms of Tv = 2π/$\sqrt {EA/\left( {{m_{n + 1}}{l_{0,n + 1}}} \right)} $1). It is seen from the checked results that the numerical procedure is trustworthy in studying the dynamics of the flexible tethered satellite system.

|
| Fig. 3 Pitch motions without any perturbations |

|
| Fig. 4 Free oscillations of sub-satellite under initial angular velocity |
Suppose that the mother satellite moves on a circle orbit of 350 km initially. The dissipation constant of tether is set as αd = 0. Consider the local down equilibrium position of the subsatellite in the orbital reference frame,i.e.,θ = 0. In this case,the eigenvalues of the Jacobian matrix are


|
| Fig. 5 Stability of local down equilibrium position without perturbations |

|
| Fig. 6 Stability of local down equilibrium position under perturbation |
Similarily,for the local upper equilibrium position,θ = π,the eigenvalues of the Jacobian matrix are
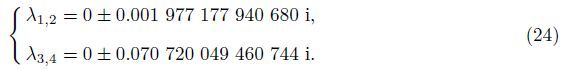

|
| Fig. 7 Stability of local upper equilibrium position |
At the same way,the two equilibrium positions along the orbit,θ = ±1.570 05,are unstable since the corresponding eigenvalues of the Jacobian matrix read

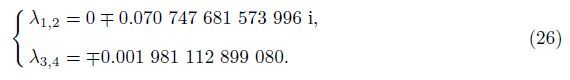

|
| Fig. 8 Motions around unstable equilibrium position when θ = 1.570 05 |

|
| Fig. 9 Motions around unstable equilibrium position for θ = −1.570 05 |
According to (11) and (12),the density of atmosphere gradually decreases with the altitude so that the influence of the air drag force becomes weaker,as shown in Fig. 10. The system parameters are listed in Table 1. The heating effect is periodic for the tethered satellite system going in and out of the shade of the Earth repeatedly. As an example,the periodic change of temperature of the tether near the sub-satellite versus time is given in Fig. 11. The lateral oscillation of sub-satellite is shown in Fig. 12. According to Fig. 12,the amplitudes of the lateral oscillation of the sub-satellite reach 17.09 m,2.07 m,0.20 m,and 36.58 m under these space perturbations,respectively. The longitudinal oscillations of the sub-satellite starting with the initial magnitudes of 0.12 m,0.16 m,0.13 m,and 6.59 m are depictured in Fig. 13, respectively. Note that the heating effect yields an almost-periodic pitch oscillation as shown in Fig. 13(d). In short,the influence of the J2 perturbation and heating effect on pitch oscillations is significant,whereas those such as the air drag force and the solar pressure strongly depend on the orbital altitude that tethered satellite system moves in.

|
| Fig. 10 Atmospheric density versus altitude |

|
| Fig. 11 Temperature of tether near sub-satellite |

|
| Fig. 12 Lateral oscillations of sub-satellite under perturbations |

|
| Fig. 13 Longitudinal oscillation of sub-satellite under perturbations |
It should be noted that the orbital eccentricity plays an important role in the dynamics of tether satellite system. Figure 14 shows the bifurcation of pitch motion with a small initial pitch angle of π150. As shown in Fig. 14,there exist abundant nonlinear phenomena in the flexible tethered satellite system. In general,quasi-periodic motions appear in an elliptic orbit with small eccentricity,whereas chaotic motions appear in a larger elliptic orbit with the eccentricity larger than 0.315 3. Using zero initial states,for example,the quasi-periodic motions can be displayed within six orbital periods for the eccentricity of 0.362 5. The quasi-periodic motions can be checked with the help of phase portrait and Poincar´e map,as shown in Figs. 15(e) and 15(f). Here,the Poincar´e section is defined as Σ = {(θ,dθ/dt)|ν = mod(2π)}. One can see from Fig. 16(a) that the sub-satellite sometimes rotates about the mother satellite and sometimes oscillates about itself in the local vertical position. An interpretation for the nonlinear dynamic feature is that the orientation of local equilibrium position of the tethered satellite system in elliptic orbits is not aligned with the gravity vector so that the gravity gradient yields a non-zero external torque about the center of mass of the tethered satellite system. As a result,the small time-variant torque that corresponds to small eccentricity yields a nonlinear dynamic behavior, as shown in Fig. 15(a),which is similar to that of a spring-mass pendulum. A non-harmonic motion like the chaotic motion in Fig. 16 appears in the case of a larger time-variant torque that corresponds to a lager eccentricity. The chaotic motion can be illustrated through the phase portrait in Fig. 16(d) and the Poincaré map in Fig. 16(e).

|
| Fig. 14 Bifurcation of pitch motion as eccentricity increases |

|
| Fig. 15 Pitch motion for small eccentricity of 0.021 8 |

|
| Fig. 16 Pitch motion for large eccentricity of 0.362 5 |
The tethered satellite system in the circular orbit keeps its local stable equilibrium if no perturbation exists. For elliptic orbits,however,the tethered satellite system cannot maintain its local equilibrium so that nonlinear dynamic phenomena occur.
5 ConclusionsThere exist four equilibrium positions for a tethered satellite system in the circular orbit. The local down-and upper vertical positions are stable,while the equilibrium positions along the orbit are unstable. In the case of elliptical orbits,there exists abundant nonlinear dynamics like quasi-periodic oscillations and chaotic motions. The J2 perturbation and the heating effect play a remarkable role in the dynamics of tethered satellite system,whereas the influence of the air drag force and the solar pressure on the dynamics of tethered satellite system strongly depends on the orbit altitude.
| [1] | Wen, H., Jin, D. P., and Hu, H. Y. Advances in dynamics and control of tethered satellite systems. Acta Mechanica Sinica, 24(3), 229-241(2008) |
| [2] | Capó-Lugo, P. A. and Bainum, P. M. Solar pressure effects for a constellation in highly elliptical orbit. Journal of Guidance, Control, and Dynamics, 32(2), 675-679(2009) |
| [3] | Sanmartín, J. R., Lorenzini, E. C., and Martínez-Sánchez, M. Electrodynamic tether applications and constraints. Journal of Spacecraft and Rockets, 47(3), 442-456(2010) |
| [4] | Zhong, R. and Zhu, Z. H. Dynamics of nanosatellite deorbit by bare electrodynamic tether in low earth orbit. Journal of Spacecraft and Rockets, 50(3), 691-700(2013) |
| [5] | Jasper, L. and Schaub, H. Input shaped large thrust maneuver with a tethered debris object. Acta Astronautica, 96(1), 128-137(2014) |
| [6] | Steiner, W. Transient chaotic oscillations of a tethered satellite system. Acta Mechanica, 127(1-4), 155-163(1998) |
| [7] | Nakanishi, K. and Fujii, H. A. Periodic motion of multi-compound-tether satellite system. Proceedings of the 56th International Astronautical Federation Congress, American Institute of Aeronautics and Astronautics, Reston (2005) |
| [8] | Nakanishi, K., Kojima, H., andWatanabe, T. Trajectories of in-plane periodic solutions of tethered satellite system projected on van der Pol planes. Acta Astronautica, 68(7-8), 1024-1030(2011) |
| [9] | Mankala, K. K. and Agrawal, S. K. Dynamic modeling and simulation of satellite tethered systems. Journal of Vibration and Acoustics, 127(2), 144-156(2005) |
| [10] | Ellis, J. R. and Hall, C. D. Out-of-plane librations of spinning tethered satellite systems. Celestial Mechanics and Dynamical Astronomy, 106(1), 39-67(2010) |
| [11] | Yu, B. S. and Jin, D. P. Deployment and retrieval of tethered satellite system under J2 perturbation and heating effect. Acta Astronautica, 67(7-8), 845-853(2010) |
| [12] | Kojima, H., Furukawa, Y., and Trivailo, P. M. Experimental verification of periodic libration of tethered satellite system in elliptic orbit. Journal of Guidance, Control, and Dynamics, 34(2), 614-618(2011) |
| [13] | Zhang, W., Gao, F. B., and Yao, M. H. Periodic solutions and stability of a tethered satellite system. Mechanics Research Communications, 44(1), 24-29(2012) |
| [14] | Jin, D. P., Wang, X. Y., and Wen, H. Quasi-periodic motion of a ground-based tethered subsatellite with attitude. Advances in the Astronautical Sciences, 145(1), 1087-1096(2012) |
| [15] | Zhong, R. and Zhu, Z. H. Libration dynamics and stability of electrodynamic tethers in satellite deorbit. Celestial Mechanics and Dynamical Astronomy, 116(3), 279-298(2013) |
| [16] | Avanzini, G. and Fedi, M. Refined dynamical analysis of multi-tethered satellite formations. Acta Astronautica, 84(1), 36-48(2013) |
| [17] | Avanzini, G. and Fedi, M. Effects of eccentricity of the reference orbit on multi-tethered satellite formations. Acta Astronautica, 94(1), 338-350(2014) |
| [18] | Williams, P., Yeo, S., and Blanksby, C. Heating and modeling effects in tethered aerocapture missions. Journal of Guidance, Control, and Dynamics, 26(4), 643-654(2003) |
 2016, Vol. 37
2016, Vol. 37



