Shanghai University
Article Information
- M. MOHAMMADIMEHR, M. A. MOHAMMADIMEHR, P. DASHTI. 2016.
- Size-dependent effect on biaxial and shear nonlinear buckling analysis of nonlocal isotropic and orthotropic micro-plate based on surface stress and modified couple stress theories using differential quadrature method
- Appl. Math. Mech. -Engl. Ed., 37(4): 529-554
- http://dx.doi.org/10.1007/s10483-016-2045-9
Article History
- Received Apr. 7, 2015;
- in final form Sept. 14, 2015
Nanotechnology is a recent development in scientific research that has a variety of industrial and purification processes. The applications of purification and environmental cleanup are such as the desalination of water,water filtration,wastewater treatment,and groundwater treatment. Industrial applications may include construction materials,military goods,and nano-machining of nano-wires,nano-rods,and single or multi-layers of graphene sheet.
The size dependent effect,such as the nonlocal elasticity theory[1, 2, 3, 4],the modified couple stress theory (MCST)[5, 6, 7],the strain gradient theory (SGT)[8, 9, 10],the modified strain gradient theory (MSGT)[11],and the surface stress effect[12, 13],plays an important role at micro-and nano-scales. In the last two decades,many researchers have investigated the effects of the mentioned fields on the buckling and vibration analysis of micro- and nano-structures.
Ke et al.[14] presented a Mindlin micro-plate model based on the MCST for the free vibration analysis of micro-plates. They used the p-version Ritz method to determine the natural frequencies of the micro-plate with various boundary conditions,and they also investigated the influence of the length scale parameter,the side-to-thickness ratio,and the aspect ratio on the free vibration characteristics of the micro-plate. It is found that the size effect is significant when the thickness of the micro-plate is close to the material length scale parameter. Murmu and Adhikari[15] analyzed the vibration of coupled nanobeam system under the initial compressive pre-stressed condition. Using Eringen’s nonlocal elasticity model,they formulated expressions for bending-vibration of pre-stressed nonlocal double-nanobeam-system (NDNBS). Their results showed that the scale effects in higher natural frequencies of the NDNBS are considerable, and the difference between the pre-loads affects the nonlocal frequency in the in-phase type and out-of-phase type vibrations mode of NDNBS. Based on Eringen’s nonlocal continuum elasticity,Analooei et al.[16] illustrated the elastic buckling and vibration characteristics of isotropic and orthotropic nanoplates using the finite strip method. Murmu et al.[17] studied the buckling of double-nanoplate-system (DNPS) subjected to biaxial compression using the nonlocal elasticity theory that the two nanoplates of DNPS are bonded by an elastic medium. Their results showed that the small-scale effect in the biaxially compressed DNPS increases with increasing values of the nonlocal parameter for the case of synchronous modes of buckling than in the asynchronous modes of buckling,and the buckling load decreases with an increase in the nonlocal parameter. Using the strain gradient elasticity theory and the generalized differential quadrature (GDQ) method,Sahmani and Ansari[18] presented the prediction of buckling behavior of size-dependent microbeams made of functionally graded materials (FGMs) including the thermal environment effect based on the third-order shear deformation beam theory. They concluded that the temperature change plays a more important role in the buckling behavior of FGM microbeams with higher values of the dimensionless length scale parameter. Xu et al.[19] investigated the nonlinear bending behavior of a bilayer graphene sheet (BLGS) under a transverse uniform load in thermal environments. They modeled the BLGS as a nonlocal double-layered plate which contains small scale effect and van der Waals (vdW) interaction forces. They estimated the small scale parameter by matching the deflections of graphene sheets observed from the molecular dynamics (MD) simulation results with the numerical results obtained from the nonlocal plate model. Their numerical results showed that the stacking sequence has a moderate effect,whereas the temperature change and the aspect ratio have a significant effect on the nonlinear bending behavior of BLGSs.
Anjomshoa[20] developed a finite element approach based on the size dependent nonlocal elasticity theory for buckling analysis of nano-scaled multi-layered graphene sheets (MLGSs) embedded in the polymer matrix. He simulated the vdW interactions between the graphene layers and the graphene-polymer as a set of linear springs using the Lennard-Jones potential model. The accuracy of the finite element analysis approved through a comparison with the MD and the analytical solutions available in the literature. He showed that the in-phase loads are independent of interlayer vdW interactions,while the out-of-phase loads depend on the vdW interactions.
Based on the MCST,Jung et al.[21] obtained an analytical solution for buckling analysis of sigmoid functionally graded material (S-FGM) nanoplates on the elastic medium. Using the nonlocal elasticity theory,Mohammadi et al.[22] analyzed the shear buckling behavior of orthotropic single-layered graphene sheets (SLGSs) in the thermal environment. Their numerical results showed that the critical shear buckling load of SLGSs is strongly dependent on the small scale coefficient. Using the nonlocal Mindlin plate theory,Golmakani and Rezatalab[23] illustrated non-uniform biaxial buckling analysis of orthotropic single-layered graphene sheet embedded in a Pasternak elastic medium where all edges of the graphene sheet are subjected to linearly varying normal stresses. They used the differential quadrature method (DQM) to solve the governing equations for various boundary conditions. Daneshmehr et al.[24] investigated a nonlocal higher order plate theory for stability analysis of nanoplates subjected to biaxial in plane loadings. They implemented the GDQ method to solve the size dependent buckling analysis according to the higher order shear deformation plate theories,where highly coupled equations exist for various boundary conditions of rectangular plates. Their results observed that the buckling load predicted by the higher order theory significantly deviates from the classical ones,especially for thick plates. Comparing the results obtained from various theories showed that as the material length scale parameter takes higher values,the difference between the buckling loads resulting from different theories declines.
Yao and Li[25] studied the nonlinear vibration of a two-dimensional (2D) composite laminated plate in the subsonic air flow with simply supported boundary conditions. Based on the von Karman’s plate theory,they obtained the equation of motion of the plate using Hamilton’s principle and induced the aerodynamic pressure by the coupled vibration of the plate,and the subsonic airflow was derived from the linear potential flow theory and compared with the existing model. Also,they used the variable separation method to transform the equation of motion of the plate into nonlinear ordinary differential equations. Moreover,they investigated the influence of the flow velocity,the length-to-thickness ratio,and the ply angle of the plate on the nonlinear vibration behaviors of the plate. They concluded that the composite laminated plate with the smaller ply angle exhibits more stable dynamic properties than that with the larger ply angles. Yao and Li[26] illustrated the bifurcation and chaotic motion of a 2D composite laminated plate with geometric nonlinearity subjected to incompressible subsonic flow and transverse harmonic excitation. Mohammadimehr et al.[27] presented the free vibration of viscoelastic double-bonded polymeric nanocomposite plate reinforced by functionally graded single-walled carbon nanotubes (FG-SWCNTs) embedded in the viscoelastic foundation based on the MSGT. They considered different distributions of SWCNTs as uniform distribution (UD),various functionally graded (FG) distributions (FG-V,FG-X,and FG-O) and defined the material properties of viscoelastic nanocomposite plates by the extended mixture rule. Also, they obtained the governing equations of motion using Hamilton’s principle and the sinusoidal shear deformation theory. Then,they determined the natural frequency of the nanocomposite plates by Navier’s and meshless methods.
In this article,preliminaries are followed to obtain the governing equations of equilibrium for the biaxial and shear nonlinear buckling analysis of the isotropic and orthotropic micro-plate based on the surface stress,the modified couple stress,and the nonlocal elasticity theories using the DQM for various boundary conditions that these boundary conditions are shown as simplysupported (S),clamped (C),and free (F) boundary conditions. The size-dependent effects such as the material length scale parameter,the nonlocal parameter,and the surface residual stress based on the modified couple stress and surface stress and Eringen’s nonlocal elasticity theories on the biaxial nonlinear buckling analysis of the orthotropic micro-plate are considered simultaneously. At the micro/nano scale,the size-dependent effects such as the material length scale parameter and the surface residual stress increase the critical buckling load,while the effect of nonlocal parameter on the critical buckling load is vice versa. Basically,the use of nano in structures leads to increasing the flexural rigidity which is predicted by the modified couple stress and the surface stress theories as well,while Eringen’s nonlocal elasticity theory does not anticipate.
2 Governing equations of orthotropic micro-plateIn this section,based on the surface stress effect,Fig. 1 shows a schematic view of the biaxial and shear buckling analysis of orthotropic rectangular micro-plate on elastic foundations (polymer matrix). Consider the orthotropic mono-layer micro-plate with the length a,the width b,and the thickness h resting on two parameter foundations. For modelling the polymer matrix,the Pasternak-type foundation model is considered which accounts for both the normal pressure and the transverse shear deformation of the surrounding elastic medium. The Cartesian coordinates system with the directions (x,y,z) is located on the mid-plane of nanoplates that the x-,y-,and z-axes are along the length,width,and thickness of the mono-layer micro-plate, respectively,where $\bar K$w and $\bar K$G are the dimensionless spring constant of Winkle type and shear constant of Pasternak type,respectively,and N x0 and N y0 depict the biaxial buckling load in the x- and y-directions,respectively.

|
| Fig. 1 Schematic view of biaxial and shear buckling analysis of orthotropic micro-plate based on surface stress effect on elastic foundations |
The displacement fields based on the classical plate theory (CPT) are defined as
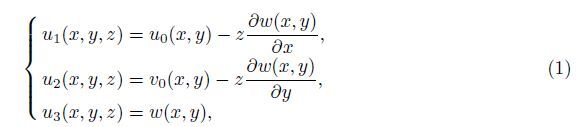
Using the nonlinear von Kármán assumption,the relationships between the strain and the displacements of the micro-plate are written as
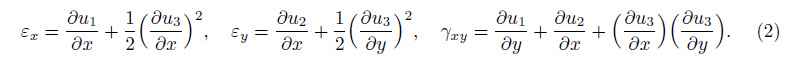
Substituting Eq. (1) into Eq. (2) yields the following nonlinear strain components[28]:
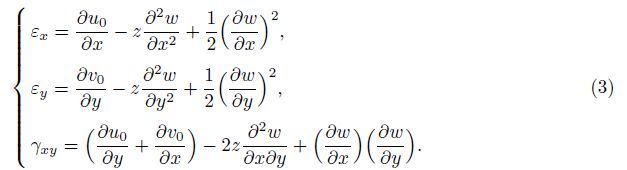
The total potential energy for the orthotropic micro-plate based on the surface stress,nonlocal, and modified couple stress theories is expressed as

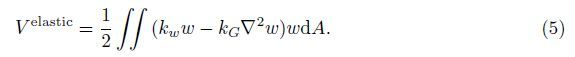
The strain energy of the orthotropic micro-plate based on the MCST is considered as
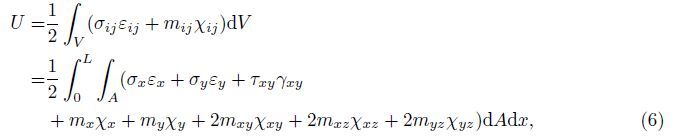
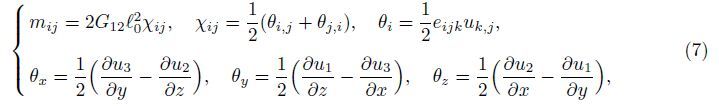
Substituting Eq. (1) into Eq. (7) yields
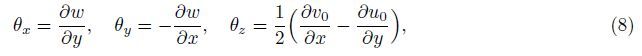
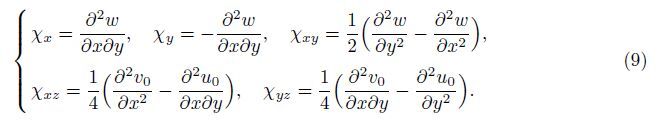
The non-zero components of stress for the bulk of the orthotropic micro-plate based on the nonlocal elasticity theory can be defined as
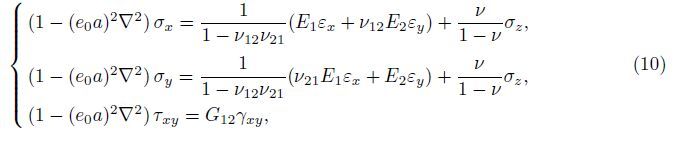
Because of the interaction between the elastic surface and bulk material,the surface constitutive equations can be written as follows:
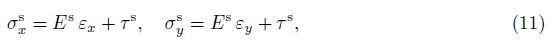

The resultant forces and moments of the orthotropic micro-plate are illustrated as
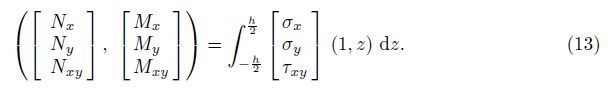
The resultant moments of the orthotropic micro-plate based on the MCST can be written as follows:
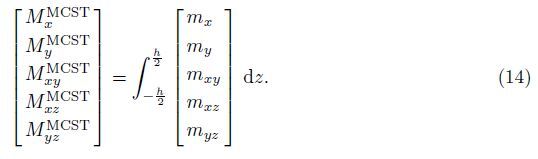
Substituting Eq. (11) into Eq. (13),one can obtain the resultant forces and moments for the elastic surface material,
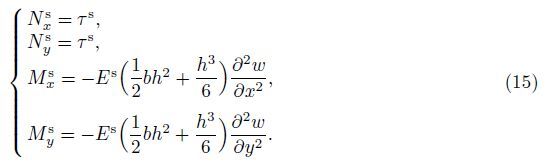
The balance conditions on the upper and lower surfaces for the biaxial and shear buckling analysis should be satisfied. Then,we have
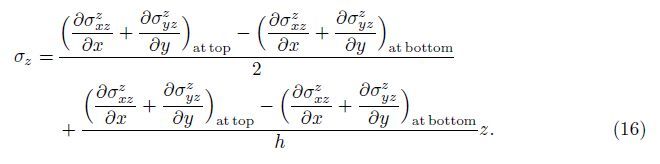
Substituting Eq. (12) into Eq. (16) yields

Substituting Eq. (17) into Eq. (10),the constitutive equations of the orthotropic micro-plate based on the nonlocal and surface stress theories are rewritten as
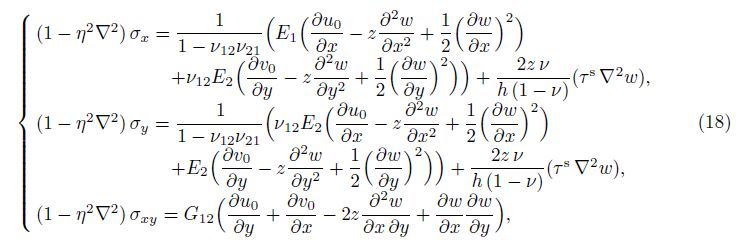
Substituting Eq. (18) into Eq. (13) yields the resultant moment of the orthotropic microplate,
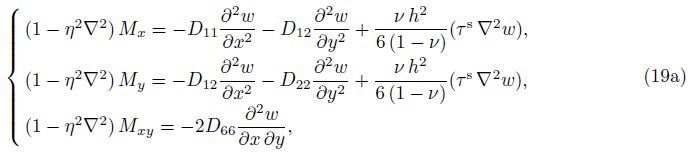
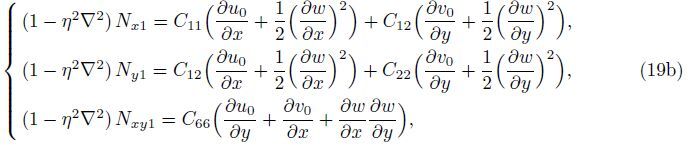
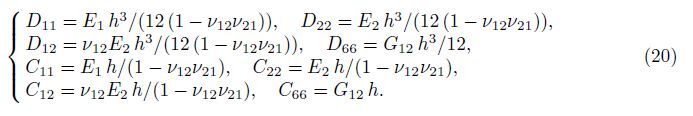
Substituting Eqs. (7)-(9) into Eq. (14) yields
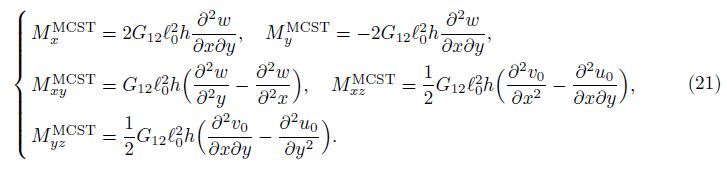
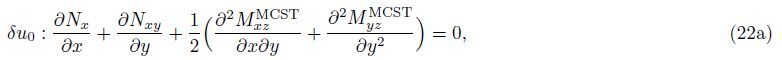
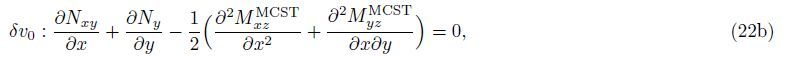
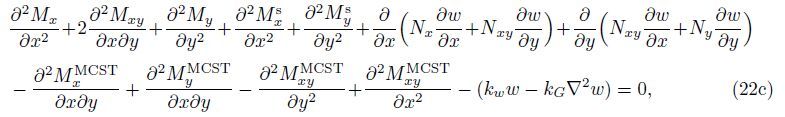
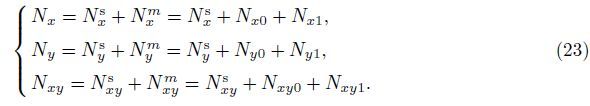
By substituting Eqs. (15),(19a),(19b),and (21) into Eqs. (22a)-(22c),the governing equation of equilibrium for the orthotropic micro-plate subjected to the in-plane forces based on various size dependant effects is obtained as follows:
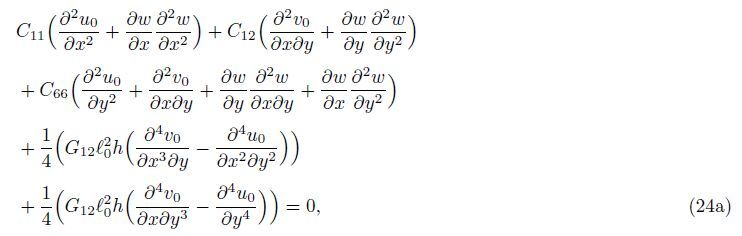
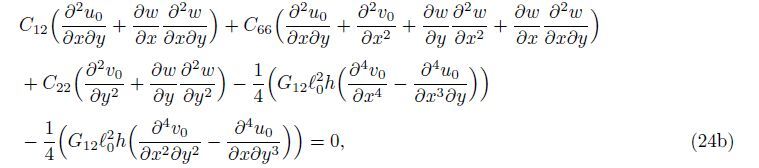
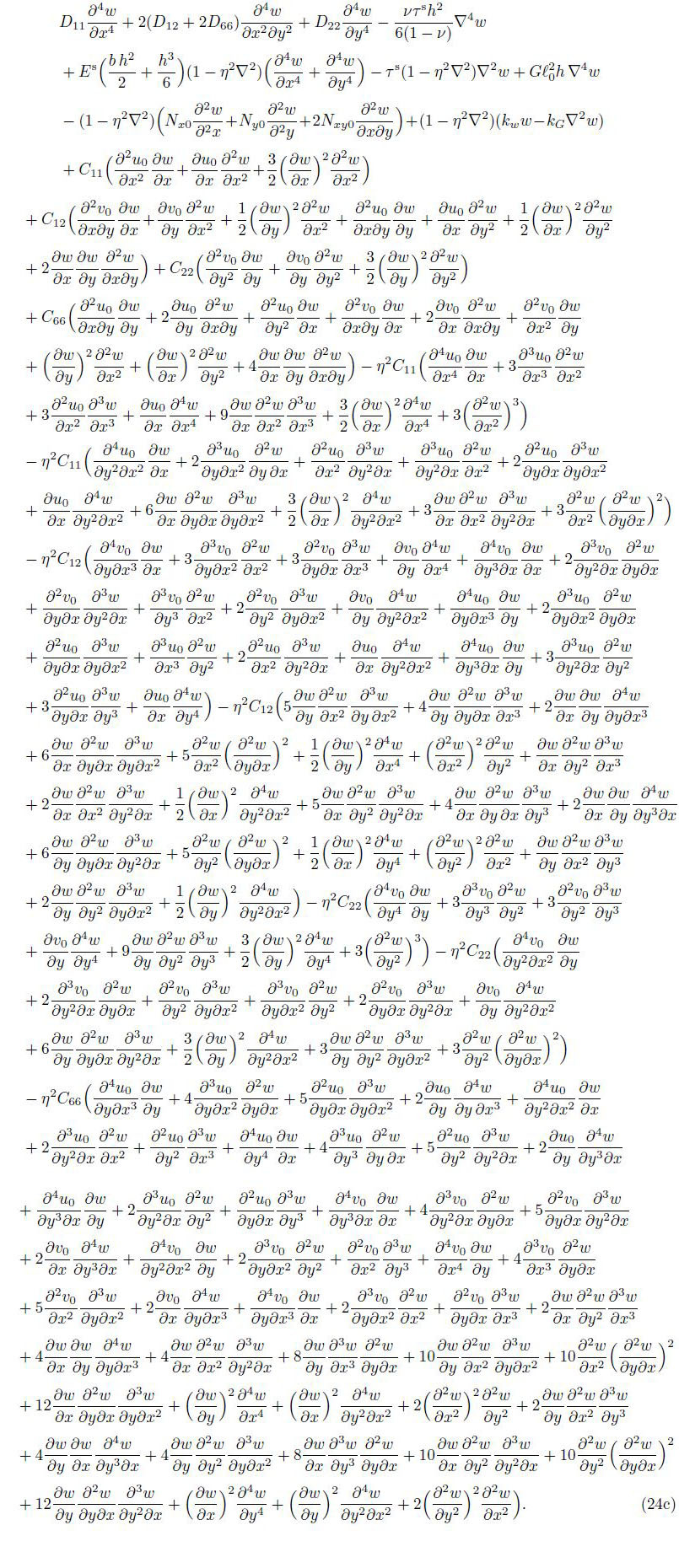
Because of convenience and generality,the dimensionless geometric and mechanical parameters for the orthotropic micro-plate can be introduced as follows:
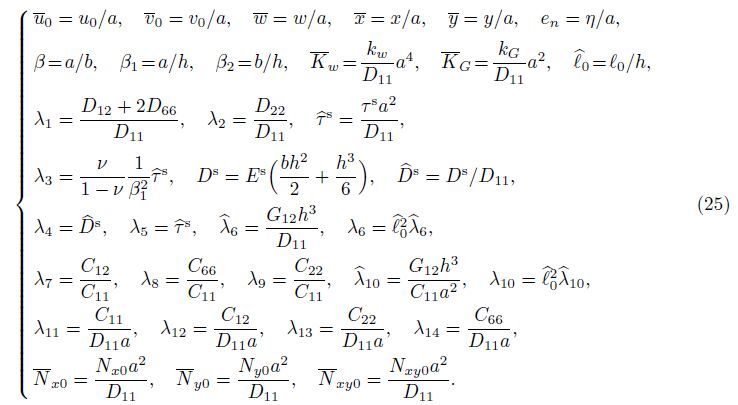
Substituting Eq. (25) into Eqs. (24a)-(24c) yields the following dimensionless equation of equilibrium for the orthotropic micro-plate:
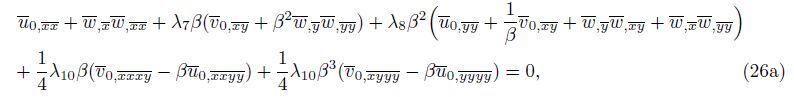
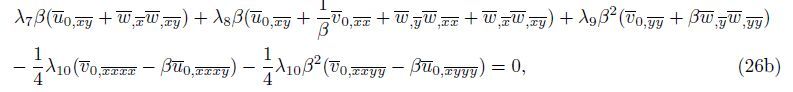

It is noted that the DQM is a powerful and efficient numerical method to solve initial and boundary value problems with respect to other numerical techniques,since this numerical method provides simple and algebraic formulation and low computational cost. Also,the DQM has been widely used to analyze mechanical behavior such as vibration and stability problems[22]. According to this method,the derivatives of a function at the point (xi,yi) can be obtained in the terms of the value of the function in the throughout domain as
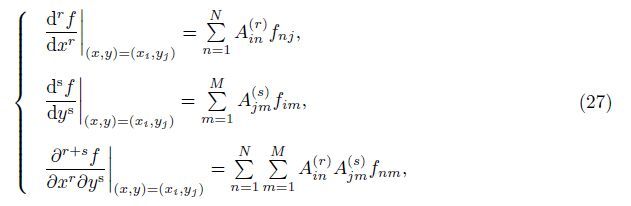

Also,the weighting coefficients of the first and higher order derivatives can be determined as follows[22, 29]:
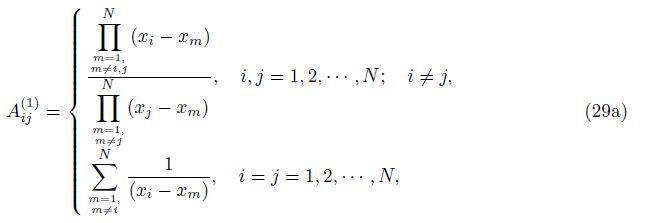
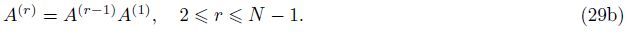
A well-accepted set of the grid points is given by the Gauss-Lobatto-Chebyshev[30] points for the interval [0,L] where the set of grid points in the terms of natural coordinate directions xi and yi are defined as
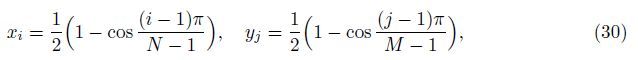
Using the differential quadrature technique,the governing equation of equilibrium for the nonlocal isotropic and orthotropic micro-plate based on the surface stress and modified couple stress theories can be obtained.
Using the differential quadrature approximation,the following boundary conditions are given.
Case 1 All edges simply supported (SSSS)
At the edges x = 0,a,
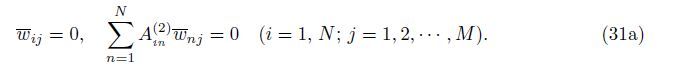
At the edges y = 0,b,
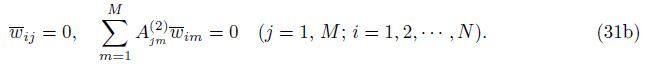
Case 2 All edges clamped (CCCC)
At the edges x = 0,a,
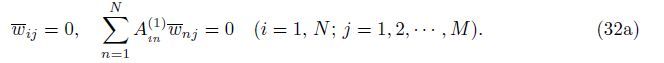
At the edges y = 0,b,
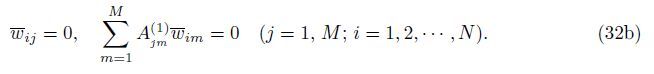
Case 3 SCSC
At the edges x = 0,a,
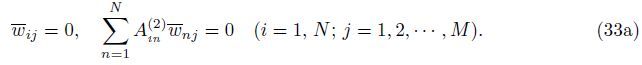
At the edges y = 0,b,
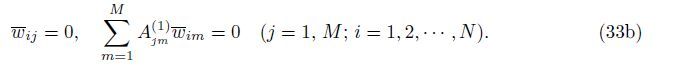
Case 4 CSCS
At the edges x = 0,a,
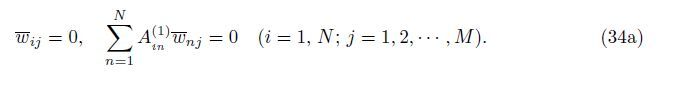
At the edges y = 0,b,
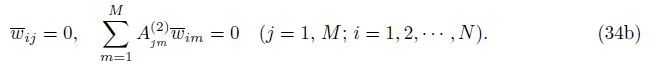
Case 5 SSSC
At the edges x = 0,a,
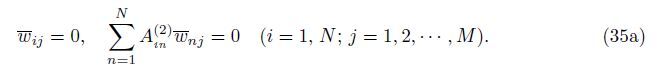
At the edge y = 0,
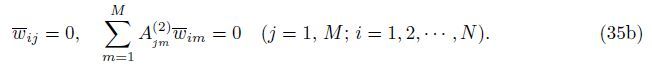
At the edge y = b,
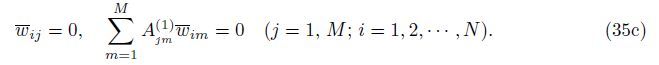
Case 6 CCCS
At the edges x = 0,a,
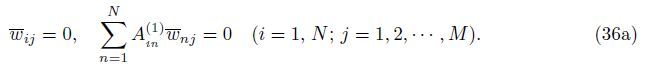
At the edge y = 0,
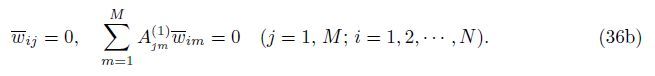
At the edge y = b,
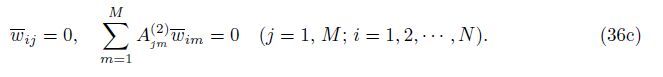
Case 7 SFSF[31]
At the edges x = 0,a,
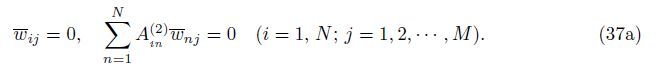
At the edges y = 0,b,
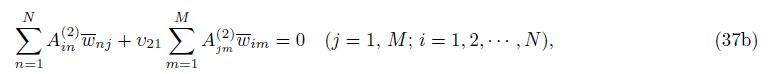
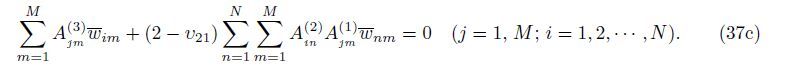
Using the DQM,an eigenvalue problem is obtained as follows:
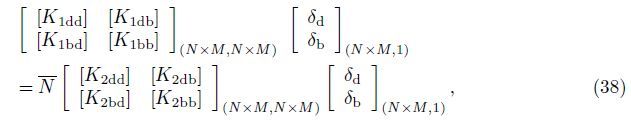
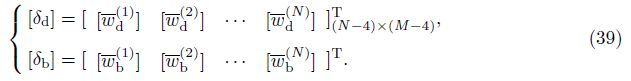
Based on the nonlocal elasticity and modified couple stress theories,the matrix form of nonlocal isotropic and orthotropicmicro-plate considering the surface stress effect can be written as
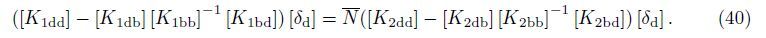
It can be written in a simply form of

Also,α is defined as follows:

To the best of the authors’ knowledge,no literature is available for uniaxial,biaxial,and shear nonlinear buckling analysis of the nonlocal isotropic and orthotropic micro-plate based on Eringen’s nonlocal elasticity,surface stress,and modified couple stress theories using the DQM. The obtained results of this research are checked by comparing the obtained results with the published works[32, 33].
Table 1 shows the comparison between the present studies for the critical shear buckling load of the isotropic plate with the other works[22, 34, 35] in various aspect ratios and SCSC boundary conditions. It is observed from Table 1 that there is good agreement between the present study and the other works[22, 34, 35].
 |
The mechanical and geometric properties for the orthotropic micro-plate embedded in an elastic medium are considered as
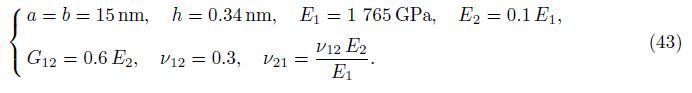
Figures 2(a) and 2(b) depict the uniaxial buckling load ratio (the nonlocal critical uniaxial buckling load with respect to the local critical uniaxial buckling load) of simply supported isotropic square micro-plates versus the Winkler modulus and shear modulus parameters for various small scale effects,respectively. The results are compared with those obtained by Pradhan and Murmu[32] and Malekzadeh et al.[33] that the excellent agreement of the results can be shown. In Fig. 2(a),the range of Winkler modulus parameter is considered as 0-400 that these ranges cover the span of a soft elastic medium (polymer matrix) to a very hard elastic medium. For the hard elastic medium,the stiffness of the springs becomes large,while for the soft elastic medium,the stiffness of the springs is small. It is concluded that the uniaxial critical buckling load ratio decreases with an increase in the small scale effect (η = e0a).

|
| Fig. 2 Uniaxial buckling load ratio of simply supported isotropic square micro-plates versus Winkler modulus (${\bar K}$G = 0) and shear modulus parameters (${\bar K}$w = 200) for various small scale effects (η = e0a) |
Based on the nonlocal elasticity theory in Fig. 3,the range of the shear modulus parameter is taken as 0-50 that these ranges cover the span of a soft elastic medium (polymer matrix) to a very hard elastic medium. Moreover,the small scale effects have been illustrated to have an increase-decrease-increase pattern with an increase in the stiffness of elastic medium.

|
| Fig. 3 Uniaxial buckling load ratio of simply supported isotropic square microplates versus shear modulus parameters (${\bar K}$w = 0) for various small scale effects |
Figure 4 reveals the effect of material length scale parameter on the uniaxial buckling load ratio (the critical uniaxial buckling load based on the MCST with respect to the local critical uniaxial buckling load) of the orthotropic micro-plate using the MCST. The influence of the material length scale parameter remains independent of the Winkler modulus parameter in its higher values for all size-dependent effects. Moreover,the material length scale parameter plays an important role in the uniaxial buckling load ratio of the orthotropic micro-plate in the soft elastic medium (polymer matrix). Also,it is shown that the critical uniaxial buckling load ratio increases with an increase in the value of material length scale parameter at a specified elastic medium. Meanwhile,considering the size dependent effect causes an increase in the stiffness of orthotropic micro-plate.

|
| Fig. 4 Effect of material length scale parameter on uniaxial buckling load ratio of orthotropic micro-plate (${\bar K}$G = 0) |
Figure 5 shows the effect of α on the critical axial buckling load. It can be seen that the critical biaxial buckling load (α = 1) is lower than the critical uniaxial buckling load (α = 0) and the difference between two cases of axial buckling load increases in the hard elastic medium.

|
| Fig. 5 Effect of α on critical axial buckling load |
The variation of the critical shear buckling load of the orthotropic micro-plate against the dimensionless Winkler modulus parameter for various boundary conditions is shown in Fig. 6.

|
| Fig. 6 Influence of various boundary conditions on critical shear buckling load of orthotropic microplate |
It is obvious that the critical shear buckling load for all edges clamped boundary conditions is higher than that for all edges simply supported boundary conditions. The effect of CCCC on the critical shear buckling load is highly prominent with respect to SSSS boundary conditions. In this state,the critical buckling load for CCCC boundary conditions leads to an increase in the stiffness of orthotropic micro-plate at the edges that the effect of this boundary conditions is more than the other boundary conditions.
Figure 7 indicates the influence of the surface residual stress on the critical uniaxial buckling load ratio (the critical uniaxial buckling load considering the surface residual stress with respect to the local critical uniaxial buckling load) of the orthotropic micro-plate. Similar to Fig. 4,the effect of the surface residual stress remains independent of Winkler modulus parameter in its higher values for all size-dependent effects. Also,it reveals that increasing the values of surface residual stress increases the critical uniaxial buckling load ratio. It is due to the fact that the surface residual stress leads to an increase in the flexural rigidity of micro-composite plate and then raises the critical uniaxial buckling load ratio.

|
| Fig. 7 Influence of surface residual stress on critical uniaxial buckling load ratio of orthotropic micro-plate for l0 = ${\bar K}$G = 0 |
The effect of Young’s modulus of the surface layer (Es) on the critical uniaxial buckling load ratio (the critical uniaxial buckling load considering Young’s modulus of surface layer with respect to the local critical uniaxial buckling load) of the orthotropic micro-plate is shown in Fig. 8. It is concluded that the effect of Es on the critical uniaxial buckling load ratio is negligible,while the effect of the surface residual stress and the material length scale parameter is noticeable according to Figs. 4 and 7.

|
| Fig. 8 Influence of Young’s modulus of surface layer on critical uniaxial buckling load ratio of orthotropic micro-plate for l0 = ${\bar K}$G = 0 |
Figures 9(a) and 9(b) explain the effect of Young’s ( E1 ) and shear ( G12 ) moduli of the orthotropic micro-plate with respect to E2 . It can be seen that an increase of ${{{E_1}} \over {{E_2}}}$ decreases the critical biaxial buckling load and vice versa for ${{{G_{12}}} \over {{E_2}}}$ .

|
| Fig. 9 Effect of ${{{E_1}} \over {{E_2}}}$ and ${{{G_{12}}} \over {{E_2}}}$ on critical biaxial buckling load of orthotropic micro-plate Fig. |
Figures 10(a) and 10(b) show the effects of the aspect ratio and the side-to-thickness ratio on the critical shear buckling load of the orthotropic micro-plate for various boundary conditions (${\bar K}$w = ${\bar K}$G = 0). It reveals that the effect of the side-to-thickness ratio remains independent of the Winkler modulus parameter for various boundary conditions,while the effect of various boundary conditions on the critical shear buckling load is considerable with the increasing aspect ratio. In this state,the stiffness of orthotropic micro-plate for CCCC boundary conditions becomes stiffer with respect to other boundary conditions.

|
| Fig. 10 Effect of various boundary conditions on critical shear buckling load for aspect ratio and side-to-thickness ratio (${\bar K}$w = ${\bar K}$G = 0) |
Figures 11 and 12 depict the influence of various boundary conditions including SSSS,CCCC, SCSC,CSCS,SSSC,CCCS,and SFSF on the critical uniaxial and biaxial buckling loads of the orthotropic micro-plate for l0 = ${\bar K}$G = 0. It is shown that the lowest and highest values of the critical uniaxial and biaxial buckling loads are related to the SFSF and CCCC boundary conditions,respectively. Such a behavior is due to the fact that the higher constraints at the edges increase the flexural rigidity of the plate,leading to a higher critical buckling load. Also,the effects of various boundary conditions on the dimensionless critical buckling load for different ${\bar K}$w and ${\bar K}$G are shown in Tables 2 and 3,respectively. Moreover,the influence of various α on the critical buckling load is considered. It is concluded that the critical biaxial buckling load is lower than two other states (α = 0,−1). The critical biaxial buckling load occurs earlier with respect to two other states. Thus,the stability of the orthotropic microplate for α = −1 is more than the uniaxial and biaxial buckling loads that can be helpful to design the micro-composite plate in the aircraft industry and other engineering applications.

|
| Fig. 11 Effect of various boundary conditions on critical axial buckling load for η = Es = τs = ${\bar K}$G = α = 0 and l = 1 nm |

|
| Fig. 12 Effect of various boundary conditions on critical biaxial buckling load for l0 = Es = τs = ${\bar K}$G = 0 and α = 1 |
 |
 |
The effects of the material length scale parameter,Eringen’s nonlocal parameter,and the surface residual stress on the critical buckling load for various boundary conditions are shown in Figs. 13,14,and 15,respectively. Also,the similar results are obtained for different α and boundary conditions in Tables 4,5,and 6. At the micro/nano scale,the size-dependent effects such as the material length scale parameter and the surface residual stress based on the modified couple stress and the surface stress theories increase the critical buckling load according to Figs. 13 and 15 and Tables 4 and 6,respectively,while the effect of the nonlocal parameter based on Eringen’s nonlocal elasticity theory on the critical buckling load is vice versa according to Fig. 14 and Table 5. Basically,the use of nano in structures leads to increasing the flexural rigidity and the critical buckling load that this behavior predicted by the modified couple stress and surface stress theories as well in Figs. 13 and 15,while Eringen’s nonlocal elasticity theory does not anticipate as well in Fig. 14.

|
| Fig. 13 Effect of material length scale parameter on critical axial buckling load for various boundary conditions considering η = Es = τs = ${\bar K}$w = ${\bar K}$G = 0 |

|
| Fig. 14 Effect of Eringen’s nonlocal parameter on critical axial buckling load for various boundary conditions considering l0 = Es = τs = ${\bar K}$w = ${\bar K}$G = 0 |

|
| Fig. 15 Effect of surface residual stress on critical axial buckling load for various boundary conditions considering η = l0 = Es = τs = ${\bar K}$w = ${\bar K}$G = 0 |
 |
 |
 |
Figures 16 and 17 show the effects of the side a and the aspect ratio a/b on the nonlinear biaxial buckling ratio (the nonlinear critical biaxial buckling load with respect to the linear critical biaxial buckling load) versus the amplitude curves of the orthotropic micro-plate based on the MCST embedded in an elastic foundation,respectively. The nonlinear biaxial buckling ratio decreases as the side a and the aspect ratio increase in Figs. 16 and 17,respectively. It is shown from Fig. 16 that the difference between the curves decreases with the increasing side a. Moreover,the effect of the nonlinear terms on the critical buckling load increases with the decreasing side a and the aspect ratio.

|
| Fig. 16 Effect of a on nonlinear biaxial buckling ratio versus amplitude curves of orthotropic micro-squareplate for η = Es = τs = 0, l0 = 1 nm, ${\bar K}$w = 400, ${\bar K}$G = 10, and α = 1 |

|
| Fig. 17 Effect of aspect ratio (β = a/b) on nonlinear biaxial buckling ratio versus amplitude curves of orthotropic microplate for η = Es = τs = 0, l0 = 1 nm, ${\bar K}$w = 400, ${\bar K}$G = 10, α = 1, and α = 15 nm |
Using the MCST,the influence of ${\bar K}$w and ${\bar K}$G on the nonlinear biaxial buckling ratio versus the amplitude curves of the orthotropic micro square plate is plotted in Figs. 18 and 19,respectively. The orthotropic micro-plate exhibits a typical “hard-spring” behavior,i.e., the nonlinear buckling ratio increases as the buckling amplitude increases. Both linear and nonlinear critical biaxial buckling loads increase as the nondimensional two parameters of elastic foundation (${\bar K}$w and ${\bar K}$G) increase,while the nonlinear buckling ratio decreases.

|
| Fig. 18 Effect of ${\bar K}$w on nonlinear biaxial buckling ratio versus amplitude curves of orthotropic micro-square plate for η = Es = τs = 0, l0 = 1 nm, ${\bar K}$G = 10, and α = 1, α = 15 nm |

|
| Fig. 19 Effect of KG on nonlinear biaxial buckling ratio versus amplitude curves of orthotropic micro-square plate for η = Es = τs = 0, l0 = 1 nm, ${\bar K}$w = 400, α = 1, and α = 15 nm |
In the present work,based on the surface stress,the MCST,and the nonlocal elasticity theories,the size-dependent effect on the uniaxial,biaxial,and shear nonlinear buckling analysis of the isotropic and orthotropic micro-plate is investigated. Based on the nonlinear von K´arm´an assumption,the governing equations of equilibrium for the micro-classical plate considering the mid-plane displacements are derived by the minimum principle of potential energy. The DQM is used to solve these equations. Then,the effects of the aspect ratio,the side-to-thickness ratio,Eringen’s nonlocal parameter,the material length scale parameter,Young’s modulus of the surface layer,the surface residual stress,the polymer matrix coefficients,and various boundary conditions on the dimensionless uniaxial,biaxial,and shear critical buckling loads are considered. The results are compared with those obtained by Pradhan and Murmu[32] and Malekzadeh et al.[33] that the excellent agreement of the results can be shown. The ranges 0- 400 and 0-50 for Winkler and shear moduli constants can cover the span of soft elastic medium (polymer matrix) to a very hard elastic medium,respectively. For the hard elastic medium, the stiffness of the springs becomes large,while for the soft elastic medium,the stiffness of the springs is small. It is concluded that the uniaxial critical buckling load ratio decreases with an increase in the small scale effect. The influence of the nonlocal (e0a) and material length scale ( l0 ) parameters and the surface residual stress ( τs ) on the critical buckling load of the micro-plate is explored. It is found from the results that the critical buckling loads are strongly sensitive to e0a,l0 ,and τs ,while the effect of Es on the critical buckling load is negligible. Also,it can be seen that the material length scale effect and the surface residual stress remain independent of Winkler modulus parameter in its higher values for all size-dependent effects. Moreover,l0 and τs play an important role in the critical buckling load of the orthotropic micro-plate in the soft elastic medium (polymer matrix). Moreover,it reveals from the results that the critical uniaxial buckling load ratio increases with an increase in the values of l0 and τs at a specified elastic medium. Meanwhile,considering the size dependent effect such as l0 and τs causes an increase in the stiffness of orthotropic micro-plate,while the effect of nonlocal parameter (η = e0a) on the critical buckling load is vice versa. Basically,the use of nano in structures leads to an increase in the flexural rigidity,which is predicted by the modified couple stress and surface stress theories,while Eringen’s nonlocal elasticity theory does not anticipate as well.
It can be seen that the critical biaxial buckling load is lower than the critical uniaxial buckling load,and the difference between the two cases decreases in the soft elastic medium. It is shown that the critical shear buckling load for CCCC boundary conditions is higher than that for SSSS boundary conditions. Also,the influence of various boundary conditions including SSSS,CCCC,SCSC,CSCS,SSSC,CCCS,and SFSF on the critical uniaxial and biaxial buckling loads of orthotropic micro-plate shows that the lowest and highest values of the critical uniaxial and biaxial buckling loads are related to the SFSF and CCCC boundary conditions,respectively. Such a behavior is due to the fact that the higher constraints at the edges increase the flexural rigidity of the plate,leading to a higher critical buckling load. It is obvious that the effect of the side-to-thickness ratio remains independent of Winkler modulus parameter for various boundary conditions,while the effect of various boundary conditions on the critical shear buckling load is more with the increasing aspect ratio. Finally,it indicates that the critical biaxial buckling load increases with an increase in ${{{G_{12}}} \over {{E_2}}}$ and vice versa for ${{{E_1}} \over {{E_2}}}$ .
Finally,in this research,the nonlinear critical biaxial buckling ratio (PNL/PL) versus the amplitude curves of orthotropic micro-plate considering some parameters such as the side a of the micro-plate,the aspect ratio (a/b),and the non-dimensional spring and shear constants of elastic foundation. It is illustrated that the nonlinear biaxial buckling ratio decreases as the side a and the aspect ratio increase,and the difference between the curves decreases with the increasing side a. Moreover,the influence of nonlinear terms on the critical buckling load increases with the decreasing side a and aspect ratio. Also,the results of the orthotropic microplate exhibit a typical “hard-spring” behavior,i.e.,the nonlinear buckling ratio increases as the buckling amplitude increases. Both linear and nonlinear critical biaxial buckling loads increase as the nondimensional two parameters of elastic foundation increase,while the nonlinear buckling ratio decreases.
Acknowledgements The authors would like to thank the referees for their valuable comments.
| [1] | Eringen, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54, 4703-4710(1983) |
| [2] | Reddy, J. N. Nonlocal theories for bending, buckling and vibration of beams. International Journal of Engineering Science, 45, 288-307(2007) |
| [3] | Farajpour, A., Shahidi, A. R., Mohammadi, M., and Mahzoon, M. Buckling of orthotropic micro/nanoscale plates under linearly varying in-plane load via nonlocal continuum mechanics. Composite Structures, 94, 1605-1615(2012) |
| [4] | Peng, X. W., Guo, X. M., Liu, L., and Wu, B. J. Scale effects on nonlocal buckling analysis of bilayer composite plates under non-uniform uniaxial loads. Applied Mathematics and Mechanics (English Edition), 36(1), 1-10(2015) DOI 10.1007/s10483-015-1900-7 |
| [5] | Akgöz, B. and Civalek, Ö. Free vibration analysis for single-layered graphene sheets in an elastic matrix via modified couple stress theory. Materials and Design, 42, 164-171(2012) |
| [6] | Mohammadimehr, M., Mohandes, M., and Moradi, M. Size dependent effect on the buckling and vibration analysis of double-bonded nanocomposite piezoelectric plate reinforced by boron nitride nanotube based on modified couple stress theory. Journal of Vibration and Control (2014) DOI 10.1177/1077546314544513 |
| [7] | Thai, H. T. and Vo, T. P. A size-dependent functionally graded sinusoidal plate model based on a modified couple stress theory. Composite Structures, 96, 376-383(2013) |
| [8] | Chorbanpour-Arani, A., Haghparast, E., Heidari-Rarani, M., and Khoddami-Maraghi, Z. Strain gradient shell model for nonlinear vibration analysis of visco-elastically coupled Boron Nitride nano-tube reinforced composite micro-tubes conveying viscous fluid. Computational Materials Science, 96, 448-458(2015) |
| [9] | Akgöz, B. and Civalek, Ö. Strain gradient elasticity and modified couple stress models for buckling analysis of axially loaded micro-scaled beams. International Journal of Engineering Science, 49, 1268-1280(2011) |
| [10] | Xu, X. J. and Deng, Z. C. Variational principles for buckling and vibration of MWCNTs modeled by strain gradient theory. Applied Mathematics and Mechanics (English Edition), 35(9), 1115-1128(2014) DOI 10.1007/s10483-014-1855-6 |
| [11] | Mohammadi, H. and Mahzoon, M. Thermal effects on postbuckling of nonlinear microbeams based on the modified strain gradient theory. Composite Structures, 106, 764-776(2013) |
| [12] | Ansari, R., Mohammadi, V., Shojaei, M. F., Gholami, R., and Rouhi, H. Nonlinear vibration analysis of Timoshenko nanobeams based on surface stress elasticity theory. European Journal of Mechanics A/Solids, 45, 143-152(2013) |
| [13] | Mohammadimehr, M., Mohammadi-Najafabadi, M. M., Nasiri, H., and Navi, B. R. Surface stress effects on the free vibration and bending analysis of the nonlocal single-layer graphene sheet embedded in an elastic medium using energy method. Proceedings of the Institution of Mechanical Engineers, Part N:Journal of Nanoengineering and Nanosystems (2014) DOI 10.1177/1740349914559042 |
| [14] | Ke, L., Wang, Y., Yang, J., and Kitipornchai, S. Free vibration of size-dependent Mindlin microplates based on the modified couple stress theory. Journal of Sound and Vibration, 331, 94-106(2012) |
| [15] | Murmu, T. and Adhikari, S. Nonlocal elasticity based vibration of initially pre-stressed coupled nanobeam systems. European Journal of Mechanics A/Solids, 34, 52-62(2012) |
| [16] | Analooei, H. R., Azhari, M., and Heidarpo, A. Elastic buckling and vibration analyses of orthotropic nanoplates using nonlocal continuum mechanics and spline finite strip method. Applied Mathematical Modelling, 37, 6703-6717(2013) |
| [17] | Murmu, T., Sienz, J., Adhikari, S., and Arnold, C. Nonlocal buckling of double-nanoplate-systems under biaxial compression. Composite Part B:Engineering, 44, 84-94(2013) |
| [18] | Sahmani, S. and Ansari, R. Size-dependent buckling analysis of functionally graded third-order shear deformable microbeams including thermal environment effect. Applied Mathematical Modelling, 37, 9499-9515(2013) |
| [19] | Xu, Y. M., Shen, H. S., and Zhang, C. L. Nonlocal plate model for nonlinear bending of bilayer graphene sheets subjected to transverse loads in thermal environments. Composite Structures, 98, 294-302(2013) |
| [20] | Anjomshoa, A., Shahidi, A. R., Hassani, B., and Jomehzadeh, E. Finite element buckling analysis of multi-layered graphene sheets on elastic substrate based on nonlocal elasticity theory. Applied Mathematical Modelling, 38, 5934-5955(2014) |
| [21] | Jung, W., Han, S., and Park, W. A modified couple stress theory for buckling analysis of S-FGM nanoplates embedded in Pasternak elastic medium. Composite Part B:Engineering, 60, 746-756(2014) |
| [22] | Mohammadi, M., Farajpour, A., Moradi, A., and Ghayour, M. Shear buckling of orthotropic rectangular graphene sheet embedded in an elastic medium in thermal environment. Composite Part B:Engineering, 56, 629-637(2014) |
| [23] | Golmakani, M. E. and Rezatalab, J. Nonuniform biaxial buckling of orthotropic nanoplates embedded in an elastic medium based on nonlocal Mindlin plate theory. Composite Structures, 119, 238-250(2015) |
| [24] | Daneshmehr, A., Rajabpoor, A., and Pourdavood, M., Stability of size dependent functionally graded nanoplate based on nonlocal elasticity and higher order plate theories and different boundary conditions. International Journal of Engineering Science, 82, 84-100(2014) |
| [25] | Yao, G. and Li, F. M. Nonlinear vibration of a two-dimensional composite laminated plate in subsonic air flow. Journal of Vibration and Control, 21, 662-669(2015) |
| [26] | Yao, G. and Li, F. M. Chaotic motion of a composite laminated plate with geometric nonlinearity in subsonic flow. International Journal of Non-Linear Mechanics, 50, 81-90(2013) |
| [27] | Mohammadimehr, M., Rousta-Navi, B., and Ghorbanpour-Arani, A. Free vibration of viscoelastic double-bonded polymeric nanocomposite plates reinforced by FG-SWCNTs using MSGT, sinusoidal shear deformation theory and meshless method. Composite Structures, 131, 654-671(2015) |
| [28] | Reddy, J. N. Mechanics of Laminated Composite Plates and Shells-Theory and Analysis, 2nd ed., CRC Press, Boca Raton (2004) |
| [29] | Shu, C. and Richards, B. E. Application of generalized differential quadrature to solve twodimensional incompressible Navier-Stokes equations. International Journal of Numerical Methods in Fluids, 15, 791-798(1992) |
| [30] | Shu, C. Differential Quadrature and Its Application in Engineering, Springer, London (2000) |
| [31] | Ventsel, E. and Krauthammer, T. Thin Plates and Shells:Theory, Analysis, and Application, Marcel Dekker, Inc., New York (2001) |
| [32] | Pradhan, S. C. andMurmu, T. Small scale effect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory. Physica E, 42, 1293-1301(2010) |
| [33] | Malekzadeh, P., Setoodeh, A. R., and Beni, A. A. Small scale effect on the thermal buckling of orthotropic arbitrary straight-sided quadrilateral nanoplates embedded in an elastic medium. Composite Structures, 93, 2083-2089(2011) |
| [34] | Cook, I. T. and Rockey, K. C. Shear buckling of rectangular plates with mixed boundary conditions. Aeronautical Quarterly, 14, 349-356(1963) |
| [35] | Bassily, S. F. and Dickinson, S. M. Buckling and lateral vibration of rectangular plates subject to in-plane loads a Ritz approach. Journal of Sound Vibration, 29, 219-239(1972) |
 2016, Vol. 37
2016, Vol. 37


