Shanghai University
Article Information
- Jun LIU, Jinchen JI, Jin ZHOU. 2016.
- Synchronization of networked multibody systems using fundamental equation of mechanics
- Appl. Math. Mech. -Engl. Ed., 37(5): 555-572
- http://dx.doi.org/10.1007/s10483-016-2071-8
Article History
- Received Nov. 17, 2015
- Revised Dec. 25, 2015
2. Department of Mathematics, Jining University, Qufu 273155, Shandong Province, China;
3. Faculty of Engineering and Information Technology, University of Technology Sydney, NSW 2007, Australia;
4. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China
In recent years,the coordinated control of multi-agent systems has received significant attention in a range of fields,including physics,biology,computer science,and control engineering[1, 2, 3]. In particular,the coordinated control of networked multibody systems modelled by Lagrangian dynamics (or networked Lagrangian systems) is of considerable interest for two main reasons. The first reason is that the networked Lagrangian systems can represent a class of networked mechanical systems due to their ability in dealing with complex systems involving multiple dynamics,such as multiple robotic manipulators,formation flying spacecrafts,and autonomous vehicles. The other is that the coordinated control of networked multibody systems has a wide range of engineering applications,especially in the complex and integrated production process,where the flexibility,reliability,manipulability,and scalability are highly required[4, 5]. Many researchers have contributed to the understanding of the coordination and synchronization of Lagrangian systems[6, 7, 8, 9, 10, 11, 12].
Coordination problems encountered in engineering can often be rephrased as the controlled synchronization (or consensus) problems of networked multi-agent systems,which aim to enhance both robustness and performance of networked control systems[13]. An important task undertaken in the coordinated control is to design an appropriate synchronization protocol (or algorithm) such that a group of interconnected dynamical systems can achieve a certain desired global behaviour of common interest through the information exchange between individual systems. As a result,a large number of synchronization protocols (or algorithms) have recently been proposed from the control theory point of view. For example,a passivity-based control framework was formulated to achieve the synchronization of networked Lagrangian systems[4]. The cooperative tracking control laws were used for multiple robotic manipulators[5]. The collision avoidance strategy was developed for the output synchronization of multiple mechanical systems with communication delays[14]. A passivity-based control law preserving Lagrangian structure was proposed to stabilize the synchronization of networked mechanical systems with unstable dynamics[15]. A distributed adaptive synchronization scheme was designed for Lagrangian networks with parametric uncertainties[7]. A distributed finite-time algorithm without velocity measurements was introduced to deal with the tracking synchronization problem of multiple Lagrangian systems[16]. A constraint control strategy was developed to realize the impulsive synchronization motion of networked open-loop multibody systems[8].
From the analytical mechanics point of view,the control of complex multibody systems can be formulated as the issue of the constrained motion of the corresponding multibody systems. Thus,the modelling and control of multibody systems can be studied using a unified methodology. The development of the equations of motion of a constrained discrete mechanical system is widely recognized to be one of the key issues in multibody dynamics. Researchers introduced the notion of generalized inverses to obtain simple and general equations of motion for constrained mechanical systems,which provides a different perspective on the constrained motion of multibody systems[17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]. The proposed approach is simple in implementation because the control forces required are the continuous functions of time and can be obtained explicitly in the closed form[20] by performing the simple operation of matrix multiplications and additions,thereby making the method attractive for real-time on-line control of nonlinear mechanical systems[19]. In addition,the modeling approach developed imposes no restrictions on the number and nature of constraints used to construct the equations of motion,and has been successfully applied in the control of complex multibody systems,including synchronization of multiple gyroscopes[20, 21],tracking control of robot in joint space[25],and tumbling control of dumbbell spacecraft systems[26].
The main objective of this paper is to investigate the controlled synchronization problem of networked multibody systems based on the framework of analytical mechanics[17, 18, 19, 29]. A novel optimal control scheme,which allows the development of a unified methodology for studying the synchronization of networked mechanical systems formulated by Lagrangian dynamics,will be developed by making use of some recent advances in analytical dynamics[19, 20, 21, 27]. The synchronization problem will be reformulated as a problem of the constrained motion of networked multibody systems. In particular,the network structure will be introduced into the control requirements by using the algebraic graph theory. The explicit closed-form equations of motion in terms of the fundamental equation of mechanics will be used to obtain a set of control forces for the synchronization of networked multibody systems (by imposing the constraints). Accordingly, the minimum forces for the synchronization of nonidentical nonlinear mechanical systems will be obtained,and a novel robust optimal control law for the complete synchronization of networked multibody systems will be derived. Stability analysis for the system over the undirected connected network topology will be carried out (the analysis procedure is also applicable for the directed network topology with a spanning tree). Finally,illustrative examples will be given to demonstrate effectiveness and easy implementation of the proposed control strategy.
2 Preliminary and fundamental equations 2.1 Notation and definitionsThroughout this paper,the following notations and definitions will be used. Let R =
(-∞,+∞) be the set of real numbers. For the vector u ∈Rn,uT denotes its transpose,the
norm of the vector u is defined as  . Rn×n stands for the set of n × n real
matrices. For the matrix A ∈ Rn×n,λmin(A) and λmax(A) denote its minimum and maximum
eigenvalues,respectively. A-1 denotes the inverse of matrix A. Assume that A is a symmetric
matrix,A > 0 (A ≥ 0) denotes the positive definite (semi-positive definite) matrix. For any
matrix B ∈ Rm×n,B+ denotes the Moore-Penrose generalized inverse of matrix B. 0n ∈ Rn
is the vector with all zeros,1n ∈ Rn is the vector with all ones,and In ∈ Rn×n is the
identity matrix of order n. A⊗B denotes the Kronecker product of matrices A and B. Matrix
dimensions,if not explicitly stated,are assumed to be compatible for algebraic operations. For
a complex number z,Re(z) and Im(z) represent its real and imaginary parts,respectively.
. Rn×n stands for the set of n × n real
matrices. For the matrix A ∈ Rn×n,λmin(A) and λmax(A) denote its minimum and maximum
eigenvalues,respectively. A-1 denotes the inverse of matrix A. Assume that A is a symmetric
matrix,A > 0 (A ≥ 0) denotes the positive definite (semi-positive definite) matrix. For any
matrix B ∈ Rm×n,B+ denotes the Moore-Penrose generalized inverse of matrix B. 0n ∈ Rn
is the vector with all zeros,1n ∈ Rn is the vector with all ones,and In ∈ Rn×n is the
identity matrix of order n. A⊗B denotes the Kronecker product of matrices A and B. Matrix
dimensions,if not explicitly stated,are assumed to be compatible for algebraic operations. For
a complex number z,Re(z) and Im(z) represent its real and imaginary parts,respectively.
In this paper,the graph theory will be used to model the interactions or communication topology among the agents of networked multibody systems. Some basic concepts of the graph theory are summarized as follows[8, 30, 31, 32, 33].
Consider a weighted directed graph G=(V ,E,A) of order N (N ≥ 2) with a set of nodes
V = (v1,v2,· · · ,vN),a set of edges E ⊂ V ×V ,and a weighted adjacency matrix A = (aij) ∈
RN×N having nonnegative adjacency elements aij . A directed edge in a directed graph is
denoted by (vi,vj ). (vi,vj) ∈ E means that the node vj can receive information from the node
vi,where vi is called as the parent node of vj,and vj is called as the child node of vi. The
element aij of the weighted adjacency matrix A is positive if and only if there is a directed
edge (vj,vi) in G,otherwise aij = 0. A directed tree is a directed graph,where every node has
exactly one parent except for one node,called the root,which has no parent but a directed path
to any other node. A directed spanning tree of a directed graph is a directed tree consisting
of all the nodes and some edges in G. On the contrary,an undirected edge in an undirected
graph is unordered,where an edge (vi,vj) denotes that vi and vj can obtain information from
one another. The adjacency matrix of an undirected graph is defined analogously except that
aij = aji for i ≠ j. The undirected graph G is said connected if any pair of distinct nodes can
be connected by an undirected path. All of the graphs are assumed to have no self-loop. The
elements of the Laplacian matrix L = (lij) ∈ RN×N associated with the graph G are defined asfollows:  aij and lij = -aij,where i ≠ j. For a directed graph,the Laplacian matrix
L is generally asymmetric,whereas for an undirected graph,the Laplacian matrix L = (lij) is
symmetric positive semidefinite.
aij and lij = -aij,where i ≠ j. For a directed graph,the Laplacian matrix
L is generally asymmetric,whereas for an undirected graph,the Laplacian matrix L = (lij) is
symmetric positive semidefinite.
The explicit equations of motion obtained in Refs. [17] and [19] provide a different perspective on the constrained motion of complex multibody systems,when the systems are forced to satisfy a set of consistent constraints,which will be introduced as follows.
An unconstrained mechanical system with independent coordinates is first considered here. The equation of motion of the system can be obtained using Lagrange’s equation or Newtonian mechanics as
where q ∈ Rn is the vector of generalized coordinates used to describe the configuration of the system,M(q,t) ∈ Rn×n is the symmetric positive definite inertia matrix (or mass matrix), and F(q, ,t) ∈ Rn is a known function (or force vector) of q,
,t) ∈ Rn is a known function (or force vector) of q, ,and t. Here,the dots denote
the differentiation with respect to the time.
,and t. Here,the dots denote
the differentiation with respect to the time.
The unconstrained system is assumed to be subjected to a set of m sufficiently smooth control requirements given by
where H is an m-vector. The control constraint described by (2) includes all the general types of holonomic and/or nonholonomic constraints. The initial conditions are assumed to satisfy the control requirements (2),i.e.,Under the assumption of sufficient smoothness,differentiating the control requirements (2) twice with respect to the time t gives rise to
where A is an m×n matrix. It is noted that each row of A arises by appropriately differentiating one of the m control requirements given in (2).The fundamental equation of motion of the constrained system that satisfies these constraints (or the controlled nominal system) can then be explicitly written as
where Here,N > 0 is a given positive definite matrix,the superscript ‘+’ denotes the Moore-Penrose generalized inverse of the matrix,and the control force Fc is employed to optimally minimize the quantity (Fc)TNFc (i.e.,the weighted norm of the active control force Fc) at each time instant[19].When the initial values do not satisfy the constraints,the control constraints can be modified
as Ḣ (q, , t) = f(H,t; α),where f(H,t; α) is an m-vector,which may contain a parameter
p-vector α. This m-vector f(H,t; α) is usually chosen in a way such that the system (2) has
the following two properties[19]: (i) H = 0 is an equilibrium point of the system; (ii) The
equilibrium point is globally asymptotically stable.
, t) = f(H,t; α),where f(H,t; α) is an m-vector,which may contain a parameter
p-vector α. This m-vector f(H,t; α) is usually chosen in a way such that the system (2) has
the following two properties[19]: (i) H = 0 is an equilibrium point of the system; (ii) The
equilibrium point is globally asymptotically stable.
Consider a network consisting of N agents described by Lagrangian dynamics as
where qi = (qi1,qi2,· · · ,qin)T ∈ Rn is the vector of the generalized coordinates for the agent
i, ∈ Rn are the vectors of the corresponding generalized velocities and accelerations,respectively,and Fi(qi,
∈ Rn are the vectors of the corresponding generalized velocities and accelerations,respectively,and Fi(qi, i,t) ∈ RN is a known nonlinear function of qi,
i,t) ∈ RN is a known nonlinear function of qi, i,and t. In the
context of mechanical vibrations,these agents are n degrees of freedom mechanical systems
whose individual systems need not to be identical. The model (7) has also been referred to as
a networked multibody system in the literature.
i,and t. In the
context of mechanical vibrations,these agents are n degrees of freedom mechanical systems
whose individual systems need not to be identical. The model (7) has also been referred to as
a networked multibody system in the literature.
Introducing a control input Ui into the right hand side of (7) gives the following controlled networked multibody system:
The main objective here is to implement a suitable control strategy of preliminary state feedback such that the motion of all the agents in the network will enter into the synchronization manifold of the controlled network (8)[25],
Then,a complete synchronization of the networked multibody system with respect to the generalized coordinates and their velocities will be realized,i.e.,for i =1,2,···,N,
It is worth mentioning that in order to generate interactions between the agents and guarantee the synchronization behavior of networked multibody systems,the Laplacian matrix L with respect to the graph G is usually used to design an appropriate synchronization control law, which plays an important role in determining the synchronization dynamics of the controlled networks[3, 33, 34].
3.2 Synchronization frameworkIn this subsection,the fundamental equations of motion in analytical dynamics developed by Udwadia and Kalaba[17],Udwadia[19],and Peters et al.[25] will be used to formulate the synchronization framework. The synchronization problem of networked multibody systems under an undirected connected graph will be firstly addressed.
With the definition of q=(q1T,q2T ,···,qNT )T,M=diag{M1,M2,···,MN},F =(F1T ,F2T ,··· ,FNT)T,and U =(U1T,U2T ,··· ,UNT)T,Eq. (8) can be rewritten in a compact vector form as
In order to demonstrate the effect of network topology on synchronization dynamics of the network,the problem of complete synchronization can be interpretedin terms of a constraint,which is explicitly given by
According to the property of the Laplacianmatrix L,it is easy to verify that the enforcing constraint (12) will make the motion of all the agents approach the synchronization manifold Λ.
In general,the initial conditions of Eq. (8) may not satisfy the constraint (12). Then,the constraint can be further modiffed by differentiating the constraint (12) twice with respect to the time t,
where c > 0and α > 0are positive constants. It is easy to note that (L ⊗ In)q =0 is an equi-librium point of Eq. (13),which is globally (exponentially) asymptotically stable (see the next subsection). The complete synchronization of networked multibody systems is then achieved.To facilitate optimal control framework for the controlled networked multibody system (11),the control force will be minimized with respect to the certain given positive definite metric N > 0,i.e.,J (t) = U TN (t)U at each time instant. By defining
the generalized accelerations can be written asThen,substituting (15) into the synchronization constraint (13) gives rise to
By utilizing fundamental equations (5) and (6),the explicit generalized control force U ,which minimizes J (t) and satisfies Eq. (13),can be obtained as
Just as stated in Ref.[20],the selection of the metric N plays a key role in determining the type of solution. For instance,in some engineering applications such as multibody dynamics and robotic control,N is often chosen to be M -2[8]. In other cases,the control force U may be required to comply with the principle of virtual displacements governedby d’Alembert’s principle for which the metric N = M -1 is usually more appropriate[19, 25].
Without loss of generality,by specifying N = M -2 in this paper,the complete control law is given by
By considering the structure of Laplacian matrix L with respect to the undirected connected graphs,the following relation can be obtained: L+L = IN -P ,where  ,and L+L2 = L. Hence,by using the property of pseudo-inverse matrix,the generalized control force can be formulated as follows:
,and L+L2 = L. Hence,by using the property of pseudo-inverse matrix,the generalized control force can be formulated as follows:
It can be seen that the synchronization of N agents of the networked multibody system will be achieved under the generalized control force Ui acting on the agent i given by (20). The control force Ui can be formulated as two components. The first component Ui1 describes the architecture of the network,which is determined by several elementary factors,such as the direct or indirectinteractions of the forces among the agents,various types of physical constraints,different configurations of communication links among agents,and a variety of network environmental factors[34]. In contrast,the secondcomponent Ui2 denotes the active control force applying on the agent i,which compels all the agents to reach the synchronized motion of the networked multibody system.
From the control theory point ofview[3],the control law Ui is a cooperative control algorithm for N agents to follow a synchronization trajectory imposed by the constraint (13). In fact,the first component Ui1 can be rewrittenas
It is easy to note that the first component Ui1 is a distributed coordinated algorithm,while the second component Ui2 is an active feedback control strategy.It is important to point out that various choices of parameters c and α,as well as the Laplacian matrix L can lead to different “paths” taken by the networked multibody systemstowards their eventual synchronization. In particular,the Laplacian matrix L plays a key role,because it determines the convergenceperformance of the trajectorygoverned by the different “paths”. Accordingly,the developed framework provides a unified and systematic analysis procedure for studying the synchronization motion of networked multi-agent systems by using analytical dynamics instead of the control theory. Thecorresponding global stability of synchronization manifold is also fully guaranteed based on the stability theory of dynamical systems,which will be discussed in the next subsection.
When the Laplacian matrix L is taken as the global coupling configuration,i.e.,
and n =1,M = InN ,it is interesting to find that the complete control law Ui given by Eq. (20) is just the same as Eq. (19) obtained in Ref.[20]. Therefore,the synchronization of multiple gyroscopes systems addressed by Udwadia and Han[20] can be treated as a special case of the present work. 3.3 Stability analysisThe stability of synchronization manifold in the controlled networked multibody system (11) is examined in this subsection. By using the complete control law (19),Eq. (11) can be rewritten as
The governedequation of synchronizedmotion for the agent i is then explicitly given by where ri = i + αqi denotes the output information of the systems,which is linear combinations of both generalized coordinate qi and velocity
i + αqi denotes the output information of the systems,which is linear combinations of both generalized coordinate qi and velocity  i for the agent i,and α is a positive constant scalar. c > 0 is a control parameter that represents the couplingstrength between agents,aij characterizes the interactionbetween agents iand j (i.e.,aij> 0if the agent i can receive the output information rj of agent j and aij= 0 otherwise)[20].
i for the agent i,and α is a positive constant scalar. c > 0 is a control parameter that represents the couplingstrength between agents,aij characterizes the interactionbetween agents iand j (i.e.,aij> 0if the agent i can receive the output information rj of agent j and aij= 0 otherwise)[20].
From the viewpoint of complex networks,the system (26) (or the system (11) with the control law (19)) can be regarded as an undirected dynamical network consistingof N linearly and diffusively coupled nonidentical agents under an additive active controller given by Eq. (22).
According to the geometrical analytic approach of synchronization manifold for coupled dynamical systems[20],the synchronization state can be defined as
and its evolution equation is given byIt will be convenient to introduce the synchronization error ei(t) = qi(t)-qsyn(t) (i = 1,2,···,N ) to examine the stability of synchronization manifold. Then,the corresponding synchronization error system can be written as
where e = (e1T,e2T,···,eNT )T.Since the Laplacian matrspan>ix L associated with an undirected connected graph G is symmetric and irreducible,it is easy to notice that L ≥0 and the rank of L is N -1. Furthermore,the matrix L has an algebraically simple eigenvalue 0,and all the other eigenvalues are positive. For brevity,these eigenvalues can be ordered as 0 = λ1 < λ2 ≤ ···≤ λN .
Let L = UJUT be the eigenvector decomposition of L,where U ∈ RN×N is a normal orthogonal matrix,and J = diag(λ1,λ2,··· ,λn). By defining v(t) = (UT ⊗ In)e(t),where v = (v1T (t),v2T (t),··· ,vNT (t))T ∈ RnN,it then follows from (29) that
It is easy to verify that all the states vi(t) (i = 2,3,· · · ,N) of the system (30) will globally, exponentially,and asymptotically converge to zero.By noting that u1  (1,1,· · · ,1)T∈RN is an eigenvector with respect to the eigenvalue
λ1 = 0,it can be obtained that v1(t) =
(1,1,· · · ,1)T∈RN is an eigenvector with respect to the eigenvalue
λ1 = 0,it can be obtained that v1(t) = = 0n. Consequently,the global stability
of synchronization manifold in the controlled networked multibody system (26) is guaranteed.
= 0n. Consequently,the global stability
of synchronization manifold in the controlled networked multibody system (26) is guaranteed.
The above analysis procedure indicates that the networked multibody system (7) with the control constraint (18) can always achieve complete synchronization with respect to the generalized coordinates and their velocities. As observed from Eq. (30),the complete synchronization of networked multibody systems depends on not only the coupling strength c,but also the algebraic connectivity λ2 of the controlled networks,which can well characterize the synchronization performance of the networks[33, 34]. In general,it is desirable to make the coupling strength as small as possible in practice. For a fixed coupling strength c,the larger the number of the algebraic connectivity λ2 is,the easier the synchronization of a networked multibody system will be. This conclusion is in excellent agreement with some empirical evidences from complex networks[3].
It should be mentioned that the above analysis procedure is also applicable to the synchronization problem of networked multibody systems with a directed spanning tree. In this case,the Laplacian matrix L associated with a directed graph G has an eigenvalue 0 with multiplicity 1,and all the other eigenvalues have positive real parts.
With the property of the Laplacian matrix L,it can be obtained that L+L2 = L − PL =  where η = (η1,η2,· · · ,ηN)T with ηi =
where η = (η1,η2,· · · ,ηN)T with ηi = 
As expected,similar to the derivation of Eq. (19),the generalized control force with respect to the directed network topology can be rewritten as
Then,the ith component of U acting on the agent i can be written as
where the first two components Ui1 and Ui2 are the same as stated in Eqs. (22) and (23),while the third component Ui3 is explicitly given by Notably,Ui3 is actually a state feedback controller based on the directed topology structure of networked multibody systems.It is assumed that ξ = (ξ1,ξ2,· · · ,ξN)T is an eigenvector with respect to the eigenvalue λ1 = 0 such that ξTL = 0NT and  By following the geometrical analytic procedure of
synchronization stability for directed coupled dynamical systems,the controlled synchronization
state can be obtained as qsyn(t) =
By following the geometrical analytic procedure of
synchronization stability for directed coupled dynamical systems,the controlled synchronization
state can be obtained as qsyn(t) =  and the corresponding synchronization error
dynamics is given by ei(t) = qi(t) − qsyn(t)(i = 1,2,· · · ,N).
and the corresponding synchronization error
dynamics is given by ei(t) = qi(t) − qsyn(t)(i = 1,2,· · · ,N).
Then,by following the same arguments as the undirected topology case,it is easy to verify that the global stability with respect to synchronization manifold is fully guaranteed if and only if the following condition holds:
where λj (j = 2,3,· · · ,N) are all the nonzero eigenvalues of the Laplacian matrix L.Based on the above discussion,it can be concluded that the synchronization motion of networked multibody systems can always be achieved by introducing the generalized control law Ui to the agent i when the directed graph has a spanning tree. The proposed control strategy given by Eqs. (31)-(33) is especially interesting as it has a clear physical interpretation. The generalized control law Ui is a combination of three control components Ui1,Ui2,and Ui3,where Ui1 is a preliminary feedback control input based on the architecture of network topology,Ui2 is an active control law imposed by Lagrangian dynamics of all the agents,and Ui3 is an additional state feedback controller exerted by the topology characteristic of directed network. The control law Ui can be considered to have two main parts. The first part Ui1 + Ui3 is a preliminary feedback control law from the control theory point of view,which describes the interactions between the agents. While the second part Ui2 denotes an active control law that needs to be applied to synchronize these agents. If specify η = 0n in Eq. (33),the third component Ui3 will vanish. Accordingly,the generalized control law (31) is a natural extension and generalization of (19) from the undirected connected graph to the directed network topology.
4 Illustrative examples and numerical simulationAs an application of the above derived theoretical results,the synchronization problem of a representative network composed of ten identical or nonidentical gyroscopes is discussed in this section,where numerical simulation with different kinds of network structures,including global coupling,nearest-neighbor,and small-world networks,is given to validate the theoretical results.
As stated in Ref.[20],the gyrodynamics has been an area of mechanics of considerable interest for more than a century in various fields of science and engineering. Due to its intrinsic and complex nonlinear dynamics,it has bee regarded as a typical model for analysis of nonlinear phenomena such as fixed points,periodic behavior,period-doubling behavior,quasi-periodic behavior,and chaotic motions. Moreover,it has a wide range of engineering applications including navigation of aircraft,rocket,and spacecraft and the control of complex mechanical systems[20].
Consider a representative network system consisting of ten identical or nonidentical gyroscopes by Lagrangian dynamics as[20]
where Pi = (αi,βi,ci,ei,γi,ωi) are the corresponding parameters. It is known from Ref.[20] that with different parameters,the solution trajectory of (31) can exhibit fixed points,periodic behavior and chaotic motions. Three different gyroscopic systems are chosen and illustrated in the (qi, i) phase plane for 100 ≤ t ≤ 200,as shown in Fig. 1. The parameter sets used
in calculations are: (a) Pchaos1 = (10,1,0.5,0.05,35.5,2)(for chaotic motion),(b) Pchaos2 =
(10.5,1,0.5,0.04,38.5,2.1)(for chaotic motion),(c) Pper=(10.5,1,0.45,0.045,36,2.05)(for periodic
motion),and the initial values are randomly chosen in the interval [−1,1].
i) phase plane for 100 ≤ t ≤ 200,as shown in Fig. 1. The parameter sets used
in calculations are: (a) Pchaos1 = (10,1,0.5,0.05,35.5,2)(for chaotic motion),(b) Pchaos2 =
(10.5,1,0.5,0.04,38.5,2.1)(for chaotic motion),(c) Pper=(10.5,1,0.45,0.045,36,2.05)(for periodic
motion),and the initial values are randomly chosen in the interval [−1,1].
 |
Fig. 1 Phase portrait (q,  ) of three gyroscopic systems for 100 ≤ t ≤ 150 ) of three gyroscopic systems for 100 ≤ t ≤ 150
|
Three kinds of network structures including global coupling,nearest-neighbor,and smallworld networks are considered,as shown in Fig. 2,and the corresponding Laplacian matrices are chosen as

 |
| Fig. 2 Topology graphs of three different networks |
In order to demonstrate the influence of both the individual dynamics and network topology on synchronization behaviors,three cases will be considered in the following.
4.1 Synchronization state of identical or nonidentical gyroscopesIn this subsection,numerical simulation with the same or different parameter values of gyroscopes will be obtained to show their effects on the synchronization state of the network composed of identical or nonidentical gyroscopes. Let the coupling strength c = 2 and the coefficient α = 1. Then,the complete control law U can be explicitly obtained from Eq. (18) if the parameter values of each gyroscope are fixed.
Two cases of identical gyroscopes are considered with the parameter sets of each gyroscope
being chosen as Pi = Pchaos2 and Pi = Pper (i = 1,2,· · · ,10),respectively. Figures 3 and 4 show
the phase portraits of the ten synchronized gyroscopes in the (qi, i) plane,i = 1,2,· · · ,10,for
100 ≤ t ≤ 150 for the networks with respect to Lgc,Lsw,and Lnc,respectively. It can be observed
that the synchronization states display the corresponding chaotic attractors and periodic orbits.
i) plane,i = 1,2,· · · ,10,for
100 ≤ t ≤ 150 for the networks with respect to Lgc,Lsw,and Lnc,respectively. It can be observed
that the synchronization states display the corresponding chaotic attractors and periodic orbits.
 |
Fig. 3 Phase portraits (qi,  i) (i = 1, 2, · · · , 10) of ten identical chaotic gyro systems superimposed
on each other with different topology graphs for 100 ≤ t ≤ 150 i) (i = 1, 2, · · · , 10) of ten identical chaotic gyro systems superimposed
on each other with different topology graphs for 100 ≤ t ≤ 150
|
 |
Fig. 4 Phase portraits (qi,  i) (i = 1, 2, · · · , 10) of ten identical periodic gyro systems superimposed
on each other with different topology graphs for 100 ≤ t ≤ 150 i) (i = 1, 2, · · · , 10) of ten identical periodic gyro systems superimposed
on each other with different topology graphs for 100 ≤ t ≤ 150
|
For the nonidentical gyroscope case,the parameter sets of ten different gyroscopes are chosen
as P1 = P2 = P3 = Pchaos1,P4 = P5 = P6 = P7 = Pchaos2,and P8 = P9 = P10 = Pper.
Figure 5 demonstrates the time response of generalized coordinates qi and velocities  i,i =
1,2,· · · ,10 for the ten different synchronized gyroscopes with respect to Lgc,where the state
variables of all the gyroscopes gradually approach to zero,indicating that the synchronization
state is zero.
i,i =
1,2,· · · ,10 for the ten different synchronized gyroscopes with respect to Lgc,where the state
variables of all the gyroscopes gradually approach to zero,indicating that the synchronization
state is zero.
 |
Fig. 5 Time histories qi and  i (i =
1, 2, · · · , 10) of ten nonidentical gyros
for 0 ≤ t ≤ 100 with respect to
Lgc i (i =
1, 2, · · · , 10) of ten nonidentical gyros
for 0 ≤ t ≤ 100 with respect to
Lgc
|
It is observed from numerical simulation that no matter whether the parameter sets of gyroscopes are the same or not,the network composed of identical or nonidentical gyroscopes can always achieve complete synchronization with respect to the generalized coordinates and velocities. However,their synchronization states are entirely different because they are related to the complex dynamics of the given gyroscope systems.
4.2 Synchronization performance of different network structuresThis subsection considers the effects of different network structures on the synchronization performance of the network of nonidentical gyroscopes. For simplicity,the parameter sets of the ten different gyroscopes are chosen the same as the case in the last subsection.
The synchronization error with respect to the generalized coordinates and velocities is introduced as

It is well known that both algebraic connectivity and coupling strength of the network can well formulate practical architecture of network topology[33]. These two parameters are thus taken as the key parameters for analyzing the synchronization performance of the network.
Figures 6 and 7 display the time response of synchronization process of generalized coordinates
qi and velocities  i (i = 1,2,· · · ,10) for ten nonidentical gyroscopes with respect to Lgc
and Lnc.
i (i = 1,2,· · · ,10) for ten nonidentical gyroscopes with respect to Lgc
and Lnc.
 |
| Fig. 6 Response of ten nonidentical gyros for 0 ≤ t ≤ 10 with respect to Lgc (α = 1, c = 3, and i = 1, 2, · · · , 10) |
 |
| Fig. 7 Response of ten nonidentical gyros for 0 ≤ t ≤10 with respect to Lnc (α = 1, c = 3, and i = 1, 2, · · · , 10) |
Figure 8 is the simulation result of the variation process of e(t) for two different connectivities. It can be seen from this figure that the global network has much stronger synchronizability than the nearest-neighbor network since the algebraic connectivity λ2(Lgc) = 10 > λ2(Lnc) = 0.382.
 |
Fig. 8 Synchronization error e =  (|qi−
qj | + | (|qi−
qj | + | i − i −  j |) for α = 1 and c = 3 with
globe coupling network (solid line) and
nearest-neighbor network (dashed line) j |) for α = 1 and c = 3 with
globe coupling network (solid line) and
nearest-neighbor network (dashed line)
|
Figure 9 exhibits the time evolution of synchronization process of generalized coordinates qi
and its velocities  i (i = 1,2,· · · ,10) for the ten nonidentical gyroscopes under Lsw with the
coupling strength c = 20 and c = 0.2,respectively. Figure 10 shows the variation of e(t) for two
different coupling strengths. The larger the coupling strength is,the easier the synchronization
of the network will be.
i (i = 1,2,· · · ,10) for the ten nonidentical gyroscopes under Lsw with the
coupling strength c = 20 and c = 0.2,respectively. Figure 10 shows the variation of e(t) for two
different coupling strengths. The larger the coupling strength is,the easier the synchronization
of the network will be.
 |
| Fig. 9 Response of ten nonidentical gyros for 0 ≤ t ≤ 20 corresponding to Lsw with respect to different coupling strengthes (α = 1, and i = 1, 2, · · · , 10) |
 |
Fig. 10 Synchronization error e =  (|qi − qj | + |
(|qi − qj | + | i − i −  j |) for α = 1 with coupling strengthes
c = 20 (solid line) and c = 0.2 (dashed line) j |) for α = 1 with coupling strengthes
c = 20 (solid line) and c = 0.2 (dashed line)
|
The above numerical simulation indicates that both the algebraic connectivity and coupling strength in networks have significant effects on the synchronization performance of the networks. Therefore,the network structure can be used to improve the synchronization performance of networked multibody systems for the purpose of practical control strategy.
4.3 Effects of active control strategy on synchronizationAs mentioned before,the generalized control law is composed of two main parts: a preliminary feedback control law and an additional active control law. The effect of the active control law on the synchronization performance will be discussed in order to demonstrate the distinguished features of the proposed control methodology.
A small-world network consisting of ten nonidentical gyroscopes,where the parameter sets of ten different gyroscopes are chosen as P1 = P2 = P3 = Pchaos1,P4 = P5 = P6 = P7 = Pchaos2 and P8 = P9 = P10 = Pper,respectively. For the sake of comparison,the synchronization problem of the small-world network will be addressed under an undirect connected graph and a directed spanning tree,respectively. For the directed topology case,the corresponding Laplacian matrix is taken as
It is easy to notice that both the undirected small-world network and the directed small-world network have the same structure,and the graph with respect to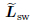 has a directed spanning
tree. By following the analysis procedure of synchronization stability,it can be concluded that
under the generalized control law Ui,the undirected connected small-world network can always
achieve complete synchronization for any coupling strength c > 0,while the directed connected
small-world network will achieve synchronization if and only if the coupling strength satisfies
c > 0.042 91α. Figures 11 and 12 present the time response of qi (i = 1,2,· · · ,10) with respect
to Lsw. In particular,Figure 11 shows the complete synchronization of the undirected smallworld
network with the active control law Ui2,whereas Fig. 12 displays the desynchronization
of such a small-world network without the active control law Ui2. Figures 13 and 14 are the
simulation results of the directed small-world network associated with
has a directed spanning
tree. By following the analysis procedure of synchronization stability,it can be concluded that
under the generalized control law Ui,the undirected connected small-world network can always
achieve complete synchronization for any coupling strength c > 0,while the directed connected
small-world network will achieve synchronization if and only if the coupling strength satisfies
c > 0.042 91α. Figures 11 and 12 present the time response of qi (i = 1,2,· · · ,10) with respect
to Lsw. In particular,Figure 11 shows the complete synchronization of the undirected smallworld
network with the active control law Ui2,whereas Fig. 12 displays the desynchronization
of such a small-world network without the active control law Ui2. Figures 13 and 14 are the
simulation results of the directed small-world network associated with 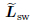 ,which yields the
same dynamic behavior as the undirected case.
,which yields the
same dynamic behavior as the undirected case.
 |
| Fig. 11 Time response of ten nonidentical gyros for 0 ≤ t ≤ 10 with respect to Lsw under control Ui1 + Ui2 |
 |
| Fig. 12 Time response of ten nonidentical gyros for 0 ≤ t ≤ 300 with respect to Lsw under control Ui1 |
 |
Fig. 13 Time response of ten nonidentical
gyros for 0 ≤ t ≤ 20 with respect to
e 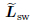 under control Ui1 + Ui2 + Ui3 under control Ui1 + Ui2 + Ui3
|
 |
Fig. 14 Time response of ten nonidentical gyros
for 0 ≤ t ≤ 100 with respect to 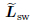 under control Ui1 + Ui3
under control Ui1 + Ui3
|
When a preliminary feedback control law Ui1+Ui3 is unable to guarantee the network synchronization of general nonidentical gyroscopes systems,an additive active control law Ui2 is required for such a purpose of control strategy. Then,the complete (global) synchronization of networked gyroscopic systems can be well guaranteed no matter whether the network topology is undirected or directed. Therefore,this paper develops a simple yet efficient control methodology to deal with the synchronization problem of networked nonidentical,highly nonlinear mechanical systems,where the developed active control strategy plays a crucial role in yielding complete synchronization of the network.
5 ConclusionsThe issue of synchronization motion of networked multibody systems is investigated in this paper with the analytical dynamics approach rather than the control theory. A novel control framework which allows the development of a unified methodology for studying the synchronization motion of networked multibody systems has been developed based on the fundamental equation of mechanics. A novel optimal control law derived from this generic framework has been applied to achieve the complete synchronization of networked multibody systems,and then the corresponding stability analysis has been fully addressed in detail. A typical network composed of ten identical or nonidentical gyroscopes with three kinds of network structures has been used to validate and visualize the theoretical results.
This paper has developed a systematic and unified methodology for studying the synchronization of networked multibody systems. Of particular note,the network structure is introduced into the control requirements with the algebraic graph theory. The proposed control strategy has a clear physical interpretation and can be divided into two main parts. The first part describes the interaction between the agents,while the second part denotes the active control force that is needed to synchronize these agents modeled by Lagrangian dynamics. It is found that,the network topology plays an important role in generating synchronization dynamics of networked multibody systems.
It should be noted that the present research is only the first step for the cooperative control of networked multibody systems in this direction. It is hoped that the approach and procedure developed in this paper could be extended to deal with the synchronization problems for more general networked multibody systems with various network topologies and coupling characteristics, such as random graph,cluster group,time varying,and delay coupling,as well as the different kinds of physical constraints and impact dynamics. This will be a more interesting and challenging topic for the future research in this direction.
| [1] | Murray, R. M. Recent research in cooperative control of multivehicle systems. Journal of Dynamic Systems Measurement and Control, 129(5), 571–583 (2007) |
| [2] | Olfati-Saber, R., Fax, J. A., and Murray, R. M. Consensus and cooperation in networked multiagent systems. Proceedings of the IEEE, 95(1), 215–233 (2007) |
| [3] | Ren, W. and Cao, Y. Distributed Coordination of Multiagent Networks: Emergent Problems, Models, and Issues, Springer-Verlag, London (2011) |
| [4] | Liu, Y. C. and Chopra, N. Controlled synchronization of heterogeneous robotic manipulators in the task space. IEEE Transactions on Robotics, 28(1), 268–275 (2012) |
| [5] | Chung, S. J. and Slotine, J. J. E. Cooperative robot control and concurrent synchronization of Lagrangian systems. IEEE Transactions on Robotics, 25(3), 686–700 (2009) |
| [6] | Hokayem, P. F., Stipanović, D. M., and Spong, M. W. Coordination and collision avoidance for Lagrangian systems with disturbances. Applied Mathematics and Computation, 217(3), 1085–1094 (2010) |
| [7] | Nuño, E., Ortega, R., Basañez, L., and Hill, D. Synchronization of networks of non-identical Lagrange systems with uncertain parameters and communication delays. IEEE Transactions on Automatic Control, 56(4), 935–941 (2011) |
| [8] | Wu, X., Zhou, J., Xiang, L., Lin, C., and Zhang, H. Impulsive synchronization motion in networked open-loop multibody systems. Multibody System Dynamics, 30, 37–52 (2013) |
| [9] | Kovriguine, D. A. Synchronization and sommerfeld effect as typical resonant patterns. Archive of Applied Mechanics, 82(5), 591–604 (2012) |
| [10] | Wen, G., Yu, W., Chen, M. Z. Q., Yu, X., and Chen, G. H∞ pinning synchronization of directed networks with aperiodic sampled-data communications. IEEE Transactions on Circuits and Systems I: Regular Papers, 61(11), 3245–3255 (2014) |
| [11] | Liu, J., Ji, J., Zhou, J., Xiang, L., and Zhao, L. Adaptive group consensus in uncertain networked Euler-Lagrange systems under directed topology. Nonlinear Dynamics, 82(3), 1145–1157 (2015) |
| [12] | Zhou, J., Wu, X., and Liu, Z. Distributed coordinated adaptive tracking in networked redundant robotic systems with a dynamic leader. Science China Technological Sciences, 57(5), 905–913 (2014) |
| [13] | Scardovi, L. and Sepulchre, R. Synchronization in networks of identical linear systems. Automatica, 45(11), 2557–2562 (2009) |
| [14] | Chopra, N., Stipanović, D. M., and Spong, M. W. On synchronization and collision avoidance for mechanical systems. American Control Conference, IEEE, Seattle (2008) |
| [15] | Nair, S. and Leonard, N. E. Stable synchronization of mechanical system networks. SIAM Journal on Control and Optimization, 47(2), 661–683 (2008) |
| [16] | Zhao, Y., Duan, Z., and Wen, G. Distributed finite-time tracking of multiple Euler-Lagrange systems without velocity measurements. International Journal of Robust and Nonlinear Control, 25(11), 1688–1703 (2015) |
| [17] | Udwadia, F. E. and Kalaba, R. E. A new perspective on constrained motion. Proceedings of the Royal Society A, 439, 407–410 (1992) |
| [18] | Udwadia, F. E. and Kalaba, R. E. What is the general form of the explicit equations of motion for constrained mechanical systems? Journal of Dynamic Systems Measurement and Control, 69, 335–339 (2002) |
| [19] | Udwadia, F. E. A new perspective on the tracking control of nonlinear structural and mechanical systems. Proceedings of the Royal Society A, 459, 1783–1800 (2003) |
| [20] | Udwadia, F. E. and Han, B. Synchronization of multiple chaotic gyroscopes using the fundamental equation of mechanics. Journal of Applied Mechanics, 75, 021011 (2008) |
| [21] | Mylapilli, H. and Udwadia, F. E. A constrained motion approach to the synchronization of multiple coupled slave gyroscopes. Proceedings of the 13th ASCE Aerospace Division Conference and the 5th NASA/ASCE Workshop on Granular Materials in Space Exploration, American Society of Civil Engineers, Pasadena (2012) |
| [22] | Udwadia, F. E. and Schutte, A. D. A unified approach to rigid body rotational dynamics and control. Proceedings of the Royal Society A, 468, 395–414 (2012) |
| [23] | Schutte, A. D. and Udwadia, F. E. New approach to the modeling of complex multibody dynamical systems. Journal of Applied Mechanics, 78, 021018 (2011) |
| [24] | Udwadia, F. E. Optimal tracking control of nonlinear dynamical systems. Proceedings of the Royal Society A, 464, 2341–2363 (2008) |
| [25] | Peters, J., Mistry, M., Udwadia, F., Cory, R., Nakanishi, J., and Schaa, S. A unifying methodology for the control of robotic systems. IEEE/RSJ International Conference: Intelligent Robots and Systems, IEEE, Edmonton (2005) |
| [26] | Schutte, A. D., Udwadia, F. E., and Lam, T. Nonlinear dynamics and control of a dumbbell spacecraft system. Proceedings of the 11th Aerospace Division International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, American Society of Civil Engineers, Long Beach (2008) |
| [27] | Udwadia, F. E. and Schutte, A. D. A unified approach to the modeling and control of multi-scale dynamical systems. Proceedings of the 13th ASCE Aerospace Division Conference on Engineering, Science, Construction, Environments and Operations in Challenging and the 5th NASA/ASCE Workshop on Granular Materials in Space Exploration, American Society of Civil Engineers, Pasadena (2012) |
| [28] | Udwadia, F. E. and Schutte, A. D. An alternative derivation of the quaternion equations of motion for rigid-body rotational dynamics. Journal of Applied Mechanics, 77, 044505 (2010) |
| [29] | Udwadia, F. E. and Kalaba, R. E. Analytical Dynamics: A New Approach, Cambridge University Press, Cambridge (1996) |
| [30] | Zhang, H., Zhou, J., and Liu, Z. Synchronization of networked harmonic oscillators with communication delays under local instantaneous interaction. Journal of Dynamic Systems Measurement and Control, 134, 061009 (2012) |
| [31] | Zhang, H. and Zhou, J. Synchronization of sampled-data coupled harmonic oscillators with control inputs missing. Systems and Control Letters, 61, 1277–1285 (2012) |
| [32] | Zhou, J., Zhang, H., Xiang, L., and Wu, X. Synchronization of coupled harmonic oscillators with local instantaneous interaction. Automatica, 48(8), 1715–1721 (2012) |
| [33] | Chen, G., Wang, X., and Li, X. Introduction to Complex Networks: Models, Structures and Dynamics, Higher Education Press, Beijing (2012) |
| [34] | Zhou, J. and Chen, T. Synchronization in generral complex delayed dynamical networks. IEEE Transactions on Circuits and Systems I: Regular Papers, 53(3), 733–744 (2006) |
 2016, Vol. 37
2016, Vol. 37






































