Shanghai University
Article Information
- T. HAYAT, M. IMTIAZ, A. ALSAEDI. 2016.
- Boundary layer flow of Oldroyd-B fluid by exponentially stretching sheet
- Appl. Math. Mech. -Engl. Ed., 37(5): 573-582
- http://dx.doi.org/10.1007/s10483-016-2072-8
Article History
- Received Aug. 17, 2015
- Revised Jan. 8, 2016
2. Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia
There are several materials like food stuffs (ketchup,mayonnaise,alcoholic beverages,chocolates in liquefies form,ice creams,yogurt,etc.),biological products (vaccines,blood,syrups, synovial fluid,etc.),and chemical products (tooth pastes,cosmetics,shampoos,paints,pharmaceutical chemicals,etc.),which do not obey Newtonian’s law of viscosity. These are characterized as the non-Newtonian fluids. The investigation of such fluids is very significant because of their relevance to practical applications in industry and engineering. Nowadays,the non- Newtonian fluids are categorized into three classes,namely,the differential,rate,and integral types. Previous information shows that much attention has been given to the differential type fluids. Because constitutive equations in the differential type fluids are much easier,and one can explicitly express the shear stresses in terms of velocity components. However,this is not the case in rate type fluids. The existed literature indicates that little attention has been given to the flows of rate type fluids. The Maxwell fluid is the simplest subclass of rate type fluid. Only the relaxation time is described by this fluid model. On the other hand,an Oldroyd-B fluid has a measurable relaxation and retardation times,and under general flow conditions, it can capture the viscoelastic features of dilute polymeric solutions. For instance,Hayat et al.[1] presented exact solutions for flow problems of an Oldroyd-B fluid. The flow of generalized Oldroyd-B fluid due to a constantly accelerating plate has been studied by Vieru et al.[2]. Qi and Jin[3] examined unsteady helical flows of a generalized Oldroyd-B fluid with the fractional derivative. The oscillating motion of an Oldroyd-B fluid between two infinite circular cylinders is studied by Fetecau et al.[4]. It is concluded that the amplitude of transient oscillations is smaller in magnitude for the case of Oldroyd-B fluid than that of the Newtonian fluid. Fetecau et al.[5] also presented energetic balance for the Rayleigh-Stokes problem of an Oldroyd-B fluid. Jamil et al.[6] investigated unsteady helical flows of an Oldroyd-B fluid. Zheng et al.[7] computed exact solutions for MHD flows of generalized Oldroyd-B fluids due to an infinite accelerating plate. Zheng et al.[8] studied magnetohydrodynamic flows of generalized Oldroyd-B fluids with slip effects. Hayat et al.[9] computed exact solutions in generalized Oldroyd-B fluids. Niu et al.[10] developed the viscoelastic effects on thermal convection of an Oldroyd-B fluid in opentop porous media. Hayat et al.[11] examined three-dimensional convective flows of Oldroyd-B fluids over the stretching surface. Shehzad et al.[12] studied the three-dimensional mixed convective radiative flow of an Oldroyd-B fluid. The flow of Oldroyd-B fluid with nanoparticles and thermal radiation has been investigated by Hayat et al.[13]. Ramzan et al.[14] computed three dimensional flows of Oldroyd-B fluids in presence of Newtonian heating. Hayat et al.[15] examined the flow of an Oldroyd-B fluid subject to homogeneous-heterogeneous reactions and Cattaneo-Christov heat flux.
Flows over the stretching surface have promising applications in several engineering processes. For example,extrusion of molten polymers through a slit die has a vital role in the production of plastic sheets and wire drawing. Moreover,glass production and paper production are some novel applications of the flows over stretched surfaces. Since the pioneering work of Crane[16] on the flows over the stretching surface,various researchers are engaged in studying such work under different aspects. It is also noticed that the stretching velocity may not be linear in all the cases. Hence,few researchers have examined the flows induced by the exponentially stretching surface. For example,Magyari and Keller[17] studied the heat and mass transport process over an exponentially stretching surface. The stagnation point flow and heat transfer due to an exponentially stretching/shrinking sheet have been presented by Bhattacharyya and Vajravelu[18]. Thermally stratified magnetohydrodynamic flows induced by an exponentially stretching sheet have been analyzed by Mukhopadhyay[19]. Pramanik[20] presented radiative flows of Casson fluids past an exponentially stretched surface. Hayat et al.[21] developed the convective flow of the nanofluid over an exponentially stretching sheet. The impact of the second-order slip on the nanofluid flow past an exponentially shrinking/stretching sheet using Buongiorno’s model has been presented by Rahman et al.[22]. Nagalakshmi et al.[23] studied effects of Hall current on the boundary layer flow induced by an exponentially stretching surface. Khan et al.[24] presented the viscoelastic flow by an exponentially stretching sheet by considering Cattaneo-Christov heat flux. Mustafa et al.[25] examined radiative flows induced by a bi-directional exponentially stretching surface.
The present study is modelled in such a way that it investigates the boundary layer flow of an Oldroyd-B fluid. Considering fluid model can capture the relaxation and retardation effects. The two-dimensional flow is created by an exponentially stretching surface. The series solution to the resulting problem is constructed,and convergence is shown using a homotopy analysis method (HAM)[26, 27, 28, 29, 30, 31, 32, 33, 34, 35]. Main attention in the discussion is focused on the analysis of relaxation and retardation time effects. Key points of the present study are summed up in the concluding section.
2 Model developmentA stretched flow of an incompressible Oldroyd-B fluid with exponential velocity and temperature distributions is presented. The governing equations in the absence of thermal radiation and viscous dissipation effects are
where u and v are the velocity components along the x- and y-directions,respectively,ν is the kinematic viscosity,Λ1 and Λ2 are the relaxation time and the retardation time,respectively, T is the temperature,and α is the thermal diffusivity. The boundary conditions are Introduce Equation (1) is satisfied automatically,and Eqs. (2) and (3) are reduced as follows: Moreover,the Prandtl number Pr,dimensionless relaxation time constant β1,and retardation time constant β2 are defined as The ratio of the conductive thermal resistance to the convective thermal resistance of the fluid is referred as the Nusselt number Nux. It gives the heat transfer rate at the surface,which is defined by where qw denotes the wall heat flux. In a dimensionless form, where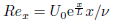 denotes the local Reynolds number.
3 Homotopic solutions
denotes the local Reynolds number.
3 Homotopic solutions
We choose the linear operators L1 and L2 and the initial guesses f0(η) and θ0(η) in the forms of
together with the properties where ci (i = 1,2,· · · ,5) are the constants. We construct the zeroth- and mth-order problems as follows: where ħf and ħθ are the nonzero auxiliary parameters. The general solutions are in which fM* and θM* denote the special solutions. 4 Convergence analysisThe HAM is employed to compute the solution of problems consisting of Eqs. (6)-(8). Auxiliary parameters ħf and ħθ play a key role in adjusting and controlling the convergence and rate of approximations for the functions f and θ. The ħ-curves of f"(η) and θ'(η) are plotted to get admissible values of ħf and ħθ at 9th-order of approximations. The admissible values of ħf and ħθ are −0.85 ≤ ħf ≤ −0.3 and −1.1 ≤ ħθ ≤ −0.3 (see Fig. 1). Further,the series solutions converge in the whole region of η (0 < η < ∞) when ħf = ħθ = −0.6 (see Table 1).
 |
| Fig. 1 ħ-curves for f and θ |
 |
Figures 2 and 3 are plotted to analyze the impact of relaxation time constant β1 and the retardation time constant β2 on the flow field f'. The effect of parameter β1 on the function f' is illustrated in Fig. 2. For larger β1,the values of f' and the boundary layer thickness decrease. This is because of the fact that a slower recovery process is observed for the higher relaxation time,which causes the boundary layer thickness to grow at a slower rate. Figure 3 depicts the effects of retardation time constant β2 on the velocity function f'. Here,when β2 is increased, the enhancement in the fluid flow and its boundary layer thickness is obtained.
 |
| Fig. 2 Impact of β1 on velocity profile |
 |
| Fig. 3 Impact of β2 on velocity profile |
Figures 4-6 are plotted for the effects of Prandtl number Pr,the relaxation time constant β1,and the retardation time constant β2 on the temperature field θ. Figure 4 shows the effects of Pr on the temperature. Reduction in the temperature field θ is observed for larger values of Pr. Influence of β1 on θ can be seen in Fig. 5. There is a decrease in θ when β1 is increased. Figure 6 represents the effect of β2 on θ. It is observed that an increase in β2 decays the temperature profile θ.
 |
| Fig. 4 Impact of Pr on temperature profile |
 |
| Fig. 5 Impact of β1 on temperature profile |
 |
| Fig. 6 Impact of β2 on temperature profile |
Table 2 is prepared to show the numerical values of surface heat transfer rate for different emerging parameters. This table shows that the Nusselt number decreases when there is an increase in the relaxation time constant β1,and it increases when the retardation time constant β2 and Prandtl number Pr are increased.
This study addresses an Oldroyd-B fluid flow generated by a stretched sheet with the exponential velocity and temperature distribution. Impacts of emerging parameters on the heat and fluid flow are examined. Following observations are made:
(ⅰ) The effects of β2 are quite opposite to those of β1 on the velocity profile f'.
(ⅱ) The temperature and thermal boundary layer thickness decay for the larger Prandtl number.
(ⅲ) The variations of β1 and β2 are qualitatively similar on the temperature profile.
(ⅳ) The Nusselt number rises for larger β2 and Pr while it reduces by increasing β1.
| [1] | Hayat, T., Khan, M., and Ayub, M. Exact solutions of flow problems of an Oldroyd-B fluid. Applied Mathematics and Computation, 151, 105–119 (2004) |
| [2] | Vieru, D., Fetecau, C., and Fetecau, C. Flow of a generalized Oldroyd-B fluid due to a constantly accelerating plate. Applied Mathematics and Computation, 201, 834–842 (2008) |
| [3] | Qi, H. and Jin, H. Unsteady helical flows of a generalized Oldroyd-B fluid with fractional derivative. Nonlinear Analysis: Real World Applications, 10(5), 2700–2708 (2009) |
| [4] | Fetecau, C., Akhtar, W., Imran, M. A., and Vieru, D. On the oscillating motion of an Oldroyd-B fluid between two infinite circular cylinders. Computers and Mathematics with Applications, 59, 2836–2845 (2010) |
| [5] | Fetecau, C., Hayat, T., Zierep, J., and Sajid, M. Energetic balance for the Rayleigh-Stokes problem of an Oldroyd-B fluid. Nonlinear Analysis: Real World Applications, 12(1), 1–13 (2011) |
| [6] | Jamil, M., Fetecau, C., and Imran, M. Unsteady helical flows of Oldroyd-B fluids. Communications in Nonlinear Science and Numerical Simulation, 16(3), 1378–1386 (2011) |
| [7] | Zheng, L., Liu, Y., and Zhang, X. Exact solutions for MHD flow of generalized Oldroyd-B fluid due to an infinite accelerating plate. Mathematical and Computer Modelling, 54, 780–788 (2011) |
| [8] | Zheng, L., Liu, Y., and Zhang, X. Slip effects on MHD flow of a generalized Oldroyd-B fluid with fractional derivative. Nonlinear Analysis: Real World Applications, 13, 513–523 (2012) |
| [9] | Hayat, T., Zaib, S., Asghar, S., and Hendi, A. A. Exact solutions in generalized Oldroyd- B fluid. Applied Mathematics and Mechanics (English Edition), 33(4), 411–426 (2012) DOI 10.1007/s10483-012-1560-7 |
| [10] | Niu, J., Shi, Z. H., and Tan, W. C. The viscoelastic effects on thermal convection of an Oldroyd-B fluid in open-top porous media. Journal of Hydrodynamics, 25, 639–642 (2013) |
| [11] | Hayat, T., Shehzad, S. A., Alsaedi, A., and Alhothuali, M. S. Three-dimensional flow of Oldroyd- B fluid over surface with convective boundary conditions. Applied Mathematics and Mechanics (English Edition), 34(4), 489–500 (2013) DOI 10.1007/s10483-013-1685-9 |
| [12] | Shehzad, S. A., Alsaedi, A., Hayat, T., and Alhothuali, M. S. Thermophoresis particle deposition in mixed convection three-dimensional radiative flow of an Oldroyd-B fluid. Journal of the Taiwan Institute of Chemical Engineers, 45(3), 787–794 (2014) |
| [13] | Hayat, T., Hussain, T., Shehzad, S. A., and Alsaed, A. Flow of Oldroyd-B fluid with nanoparticles and thermal radiation. Applied Mathematics and Mechanics (English Edition), 36(1), 69–80 (2015) DOI 10.1007/s10483-015-1896-9 |
| [14] | Ramzan, M., Farooq, M., Alhothuali, M. S., Malaikah, H. M., Cui, W., and Haycot, T. Three dimensional flow of an Oldroyd-B fluid with Newtonian heating. International Journal of Numerical Methods for Heat and Fluid Flow, 25(1), 68–85 (2015) |
| [15] | Hayat, T., Imtiaz, M., Alsaedi, A., and Almezal, S. On Cattaneo-Christov heat flux in MHD flow of Oldroyd-B fluid with homogeneous-heterogeneous reactions. Journal of Magnetism and Magnetic Materials, 401, 296–303 (2016) |
| [16] | Crane, L. J. Flow past a stretching plate. Zeitschrift für Angewandte Mathematik Und Physik, 7, 21–28 (1961) |
| [17] | Magyari, E. and Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. Journal of Physics D: Applied Physics, 32, 577–585 (1999) |
| [18] | Bhattacharyya, K. and Vajravelu, K. Stagnation-point flow and heat transfer over an exponentially shrinking sheet. Communications in Nonlinear Science and Numerical Simulation, 17, 2728–2734 (2012) |
| [19] | Mukhopadhyay, S. MHD boundary layer flow and heat transfer over an exponentially stretching sheet embedded in a thermally stratified medium. Alexandria Engineering Journal, 52, 259–265 (2013) |
| [20] | Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Engineering Journal, 5, 205–212 (2014) |
| [21] | Hayat, T., Imtiaz, M., Alsaedi, A., and Mansoor, R. MHD flow of nanofluids over an exponentially stretching sheet in a porous medium with convective boundary conditions. Chinese Physics B, 23, 054701 (2014) |
| [22] | Rahman, M. M., Rosca, A. V., and Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking/stretching surface with second order slip using Buongiorno's model. International Journal of Heat and Mass Transfer, 77, 1133–1143 (2014) |
| [23] | Nagalakshmi, C., Nagendramma, V., Sreelakshmi, K., and Sarojamma, G. Effects of Hall currents on the boundary layer flow induced by an exponentially stretching surface. Procedia Engineering, 127, 440–446 (2015) |
| [24] | Khan, J. A., Mustafa, M., Hayat, T., and Alsaedi, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface, PLoS One, 10(9), e0137363 (2015) |
| [25] | Mustafa, M., Mushtaq, A., Hayat, T., and Alsaedi, A. Radiation effects in three-dimensional flow over a bi-directional exponentially stretching sheet. Journal of the Taiwan Institute of Chemical Engineers, 47, 43–49 (2015) |
| [26] | Turkyilmazoglu, M. Solution of the Thomas-Fermi equation with a convergent approach. Communications in Nonlinear Science and Numerical Simulation, 17, 4097–4103 (2012) |
| [27] | Hatami, M., Nouri, R., and Ganji, D. D. Forced convection analysis for MHD Al2O3-water nanofluid flow over a horizontal plate. Journal of Molecular Liquids, 187, 294–301 (2013) |
| [28] | Rashidi, M. M., Ali, M., Freidoonimehr, N., Rostami, B., and Hossian, A. Mixed convection heat transfer for viscoelastic fluid flow over a porous wedge with thermal radiation. Advances in Mechanical Engineering, 204, 735939 (2014) |
| [29] | Abbasbandy, S., Yurusoy, M., and Gulluce, H. Analytical solutions of non-linear equations of power-law fluids of second grade over an infinite porous plate. Mathematical and Computational Applications, 19, 124–133 (2014) |
| [30] | Abolbashari, M. H., Freidoonimehr, N., Nazari, F., and Rashidi, M. M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nanofluid. Powder Technology, 267, 256–267 (2014) |
| [31] | Xu, H. and Pop, I. Mixed convection flow of a nanofluid over a stretching surface with uniform free stream in the presence of both nanoparticles and gyrotactic microorganisms. International Journal of Heat and Mass Transfer, 75, 610–623 (2014) |
| [32] | Hayat, T., Imtiaz, M., and Alsaedi, A. Partial slip effects in flow over nonlinear stretching surface. Applied Mathematics and Mechanics (English Edition), 36, 1513–1526 (2015) DOI 10.1007/s10483-015-1999-7 |
| [33] | Hayat, T., Shafiq, A., Nawaz, M., and Alsaedi, A. MHD axisymmetric flow of third grade fluid between porous disks with heat transfer. Applied Mathematics and Mechanics (English Edition), 33(6), 749–764 (2012) DOI 10.1007/s10483-012-1584-9 |
| [34] | Sui, J., Zheng, L., Zhang, X., and Chen, G. Mixed convection heat transfer in power law fluids over a moving conveyor along an inclined plate. International Journal of Heat and Mass Transfer, 85, 1023–1033 (2015) |
| [35] | Farooq, U., Zhao, Y. L., Hayat, T., Alsaedi, A., and Liao, S. J. Application of the HAM-based mathematica package BVPh 2.0 on MHD Falkner-Skan flow of nanofluid. Computers and Fluids, 111, 69–75 (2015) |
 2016, Vol. 37
2016, Vol. 37






























 for some values of β1, β2, and Pr
for some values of β1, β2, and Pr
