Shanghai University
Article Information
- Chunqiu WEI, Zhizhong YAN, Hui ZHENG, Chuanzeng ZHANG. 2016.
- RBF collocation method and stability analysis for phononic crystals
- Appl. Math. Mech. -Engl. Ed., 37(5): 627-638
- http://dx.doi.org/10.1007/s10483-016-2076-8
Article History
- Received Sept. 7, 2015
- Revised Nov. 10, 2015
2. Beijing Key Laboratory on MCAACI, Beijing Institute of Technology, Beijing 100081, China;
3. Department of Civil Engineering, University of Siegen, Siegen D-57076, Germany
Phononic crystals (PCs) are periodic structural materials which appeal to great attentions in these years[1]. It is well-known that when elastic waves travel through the PC,the elastic constants of the composite structure will cause the band gap where the elastic wave propaga-tion is prohibited.Such materials should have many potential applications as elastic-acoustic filters,mirrorsor transducers. The numerical methods developed for PCs energy band calcula-tion include the plane wave expansion (PWE) method[2, 3],the multi-scattering theory (MST) method[4, 5],the wavelet method[6, 7],the finite difference time domain (FDTD) method[8, 9, 10, 11, 12, 13, 14, 15],the finite element method (FEM)[16, 17] and so on. However,most of these works are not so efficient when facing the high dimensional problems,an easy new numerical method that can overcome the high dimensionproblems is quite needed.
The radial basis function (RBF) has been used successfully in scattered data interpolation,andthe introduction of the RBF to the collocation method for solving partial differential equations (PDEs) can be traced back to 1992[18],and it has many advantages,for example,the method is truly meshless method,does not require any meshes,easy to implement,high accuracy,and can transfer the high dimensional problems into one dimensional ones. Many new collocation methods are developed based on the RBF[19, 20, 21, 22]. In general,the RBF collocation methods can be divided into the boundary-type and domain-type. The difference between these two methods is depending on whether the fundamental solution has been used or not. The boundary-type methods use the fundamental solutions which already satisfy the governing equations so that only boundary points should be known,including the method of fundamental solutions(MFS)[19] ,the boundary knot method (BKM)[20] and so on [21, 22] .
While the domain-type methods do not use the fundamental solutions so that the inner points should be used to calculate the governing equations,the well-known domain-type meth-ods include the Kansa method,method of particular solutions and so on[18, 23]. The domain-type methods have the advantages of easy coding,which are more attractive in the engineering problems[24, 25]. However,the stability of the domain-type methods varies with different specific problems. It is necessary to check how the RBF method works in solving the PCs. As far as we know,it is the first time to use the strong form RBF collocation method in the PCs.
In this paper,we introduce the Kansa method to solve the PC problems,and the general form of RBF collocation methods for periodic conditions is firstly proposed by importing a con-tinuity condition. The stability will be fully discussedbased on the inverse multi-quadric(MQ),Gaussian,and MQ RBFs. In Section 2,a brief introduction of the Kansa method will be pre-sented. The generalform of Kansa method for PC will be given in Section 3. The numerical results will be fully discussedby comparison with the exact analytical solutions in Section 4. Then,some remarks will be given in the last section.
2 RBF collocation methodIn the Kansa method,the general solution u(x) is approximated by
where N is the number of all knots,ϕ is the RBF that we choose,and αi are the unknown coefficients that we need to compute. Normally,the RBFs are as follows: where r = ‖x -xi‖ is the Euclidean distance,and cs is the shape parameter that we need to choose. With the above RBFs,the normal problems can be represented as follows: where N1,Nb1,and Nb2 are the numbers of the knots on the Ω,boundaries Γ1 and Γ2,respec-tively,Ω is the problem domain,Γ1 is the Neumann boundary,Γ2 is the Dirichlet boundary,and L,B,and G are the differential operators in Ω,Γ1,and Γ2,respectively. When the unknown coefficients αi are calculated with Eqs. (5a)-(5c),the other information can also be evaluated. 3 RBF for PCsFigure 1 is one infinitely long periodical composite structure that consists of the materials 1 and 2. It can be considered as a 1D PC when the length along the y-direction is much smaller than that along the x-direction of the materials. In 1D PCs,the wave propagation can be described as
 |
| Fig. 1 1D PC |
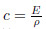 is the wave speed. According to the Bloch theory,the general solution of (8) can be written as
is the wave speed. According to the Bloch theory,the general solution of (8) can be written as where
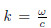 is the wave number of the P-wave. Using Eq. (9),the boundary conditions in Fig. 1 can be presented as follows:
where
is the wave number of the P-wave. Using Eq. (9),the boundary conditions in Fig. 1 can be presented as follows:
where 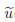 (x)1 means that the solution
(x)1 means that the solution 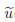 (x) belongs to the left side,while
(x) belongs to the left side,while 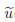 (x)r means that the solution belongs to the right side. When x =d1,we introduce the continuity conditions
(x)r means that the solution belongs to the right side. When x =d1,we introduce the continuity conditions By importing (1) into (10),(11),and (8),we can formulate the general form of RBF for the periodical composite structure as follows: where N1 and N 2 are the point numbers that are distributed in the materials 1 and 2,respec-tively. ϕ1(xi ) and ϕ2(xn) are the RBFs that areused in the materials1 and 2,respectively. By takingthe matrix (12) as an eigenvalue problem,the eigenvalue
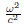 could be evaluated very simply.
4 Numerical results and discussion
could be evaluated very simply.
4 Numerical results and discussion
In this section,to check the efficiencyand the stability of the RBF method,we conduct the detailed computation for the Au/epoxy PCs. The materials used in the calculation are Au (as the material 1) and epoxy (as the material 2),the material parameters are: ρ =19 500 kg/m3,cl = 3 360 m/s,ct= 1 239 m/s for Au; ρ = 1 180 kg/m3,cl = 2 535 m/s,ct = 1 157 m/s for epoxy,and the length ratio d1 : d2 = 1 : 1,where ρ,cl,and ctare the density,the longitudinal velocity,and the transverse sound velocity,respectively. The relative errors will be defined as follows:
where n is the knot number,and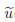 and
and 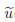 exact are the numerical result and the exact analytical solution based on the characteristic equation method,respectively. We define the lines from the low frequency to the high frequency as the lines 1 to 4 in Fig. 1. For example,the frequency line which lies between 0 and 5 is the line 1,while the line 4 is the frequency line between 15 and 20 in Fig. 1. All the results will be compared with the exact solutions.
4.1 Testing resultsof inverse MQ RBF
exact are the numerical result and the exact analytical solution based on the characteristic equation method,respectively. We define the lines from the low frequency to the high frequency as the lines 1 to 4 in Fig. 1. For example,the frequency line which lies between 0 and 5 is the line 1,while the line 4 is the frequency line between 15 and 20 in Fig. 1. All the results will be compared with the exact solutions.
4.1 Testing resultsof inverse MQ RBF
In Table 1,we will give the errors of different lines with varied shape parameters cs in a fixed point number n = 19 of inverse MQ RBF,and Fig. 2 is the figure along with Table 1.
 |
| Fig. 2 Effects of shape parameters on band structures obtained by inverse MQ RBF |
In Table 1 and Fig. 2,the numerical errors of the RBF method using the inverse MQ RBF are presented. As shown above,when cs = 0.8,Fig. 2(a) shows that the results are unstable at high frequencies,although the results at the low frequenciesin Table 1 are good enough. When the shape parameter is increasedto 0.9,the results at high frequencies in Fig. 2(b) are more stable than those in Fig. 2(a). Therefore,it is easy to know that as the shape parameter increases,theresults are becoming more stable in the inverse MQ RBF. When the shape parameter is increased to 1.5,the results are stable in the higher frequency domains,however,the correctnessof the results is worse than others,as shown in Table 1. These results are the same as those of our previous work in the time domain[26],which is using a fixed number of knots,if the absolute value of ϕ(cs) monotonically increases with cs,then a larger shape parameter cs will lead to the better but more unstable results,while a smaller shape parameter cs will give rise to the worse butmore stable results. If the absolute value of ϕ(cs) monotonicallydecreases with cs,then a larger shape parameter cs will get the worse but more stable results,while a smaller shape parameter cs will have the better but more unstable results.However,when n = 19,the shape parameter from 0.9 to 1.5 always works well at the low frequency.
Then,we present the effects of the knots number in Table 2 and Fig. 3. The shape parameter is fixed with cs = 1.
 |
| Fig. 3 Effects of knot numbers and shape parameters on band structures obtained by inverse MQ RBF |
From Table 2 and Fig. 3,we find that an increase in the node number will lead to the better butmore unstable results with a fixed shape parameter. However,if the shape parameter of inverse MQ RBF increases along with the increase of the knots number,theresults will be much better,just like Fig. 3(d).
4.2 Testing resultsof Gaussian RBFIn this section,we will also check the Gaussian RBF. From Eq. (4),it is easy to see that the absolute value of ϕ(cs) of GaussianRBF monotonicallyincreases with cs. Therefore,a larger shapeparameter cs will lead to the better but more unstable results,while a smaller shape parameter cs will give rise to the worse but more stable results.The numerical results of the Gaussian RBF with different shape parameters are presented in Table 3 and Fig. 4.
 |
| Fig. 4 Effects of shape parameters on band structures obtained by Gaussian RBF |
From Fig. 4 and Table 3,we can see that when n =19,the shape parameter between 0.3 and 0.6 always leads to stable results. The results of cs = 0.2 in Table 3 and Fig. 4(a) are not stable. When cs = 0.3,the results are not good enough in Table 3,however,it is the most stable in Fig. 4,especially in the high frequency,as shown in Fig. 4(b). As the shape parameter increases,the results are becoming better in Table 3,however,the stability is becoming worse. This resultis exactly the same as that we have assumed before. We also find that another interesting thing is that when n = 19,the good results at the frequency of over 20 cannot be obtained,however,this can be solved after the knot number is increased,as shown in Fig. 5(d).
 |
| Fig. 5 Effects of knot numbers and shape parameters on band structures obtained by Gaussian RBF |
In Fig. 5 and Table 4,the effects of different knot numbers with a fixed shape parameter cs = 0.4 in the Gaussian RBF are presented. It could be easily concluded from Fig. 5 that an increase in the node number will have the better but more unstable results.If we decrease the shape parameter,the unstable situation will be better,as shown in Figs. 5(c) and 5(d),and this is different from the inverse MQ RBF. Moreover,the results are also the same as those we have assumed at the beginning.
Figure 6 and Table 5 present the results of the shape parameter testing of MQ RBF. From Eq. (2),it is easy to see that the absolute value of ϕ(cs) of MQ RBF monotonicallyincreases with cs. Therefore,the assumption will be the same as that of the Gaussian RBF.
 |
| Fig. 6 Effects of shape parameters on band structures obtained by MQ RBF |
As shown in Fig. 6(c) and Fig. 6(d),we can see from Table 5 that when the shape parameter increases from 0.5 to 1,it works well in the low frequency. However,when cs = 1.2,the results of Fig. 5(c) are very unstable in the high frequency domain,unless the shape parameter is decreased to 1. From Fig. 6,we can see that when cs = 0.4,the results are the most stable while when cs = 1.2,the results are the most unstable. Moreover,from Table 5,we can see that the results of cs = 0.4 are the worst in accuracy by comparingthose of cs = 1.2 with the mostcorrect results. Thisis the same as what is concluded from the Gaussian RBF testing.
Figure 7 and Table 6 show the effects of the knots number with a fixed shape parameter cs = 0.7. In Fig. 7 and Table 6,the effects of different knot numbers with a fixed shape parameter cs = 0.7 are presented. It could be easily concluded that an increase in the node number will have the better but more unstable results in the MQ RBF,just as shown in Fig. 7. If we decrease the shape parameter,the unstable situation will be better,as shown in Fig. 7(c) andFig. 7(d). This is also the same as that we have assumed at first.
 |
| Fig. 7 Effects of knot numbers and shape parameters on band structures obtained by MQ RBF |
According to the above tests,we can easily find that in the RBF simulation of PCs,a large node number is necessary if we want to get more correct results in the high frequency. The shape parameter effects analysing experienceis obtained in PCs,which is that an increase in the node number will have the better but more unstable results in PC simulation. If the absolute value of ϕ(cs) monotonically increases with cs,then a large shape parameter cs will lead to the better but more unstable results,while a smaller shape parameter cs will give rise to the less accurate but more stable results. If the absolute value of ϕ(cs) monotonicallydecreases with cs,then a large shape parameter cs will yield the less accurate but more stable results,while a smaller shape parameter cs will provide the better but more unstable results.
| [1] | Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Physical Review Letters, 71, 2022–2025 (1993) |
| [2] | Sigalas, M. M. Elastic wave band gap and defect states in two-dimensional composites. Journal of the Acoustical Society of America, 101, 1256–1261 (1997) |
| [3] | Ni, Z. Q., Zhang, Z. M., Han, L., and Zhang, Y. Study on the convergence of plane wave expansion method in calculation the band structure of one dimensional typical phononic crystal. Opoelectronics and Advanced Materials—Rapid Communications, 6, 87–90 (2012) |
| [4] | Kafesaki, M. and Economou, E. N. Multiple-scattering theory for three-dimensional periodic acoustic composites. Physical Review B, 60, 11993–12001 (1999) |
| [5] | Liu, Z. Y., Chan, C. T., Sheng, P., Goertzen, A. L., and Page, J. H. Elastic wave scattering by periodic structures of spherical objects: theory and experiment. Physical Review B, 62, 2446–2457 (2000) |
| [6] | Yan, Z. Z. and Wang, Y. S. Wavelet-based method for calculating elastic band gaps of twodimensional phononic crystals. Physical Review B, 74, 224303 (2006) |
| [7] | Yan, Z. Z., Wang, Y. S., and Zhang, C. Z. Wavelet method for calculating the defect states of two-dimensional phononic crystals. CMES-Computer Modeling in Engineering and Sciences, 38, 59–87 (2008) |
| [8] | Tanaka, Y., Tomoyasu, Y., and Tamura, S. Band structure of acoustic waves in phononic lattices: two-dimensional composites with large acoustic mismatch. Physical Review B, 62, 7387–7392 (2000) |
| [9] | Khelif, A., Djafari-Rouhani, B., Vasseur, J. O., Deymier, P. A., Lambin, P., and Dobrzynski, L. Transmittivity through straight and stublike waveguides in a two-dimensional phononic crystal. Physical Review B, 65, 174308 (2002) |
| [10] | Khelif, A., Choujaa, A., Djafari-Rouhani, B., Wilm, M., Ballandras, S., and Laude, V. Trapping and guiding of acoustic waves by defect modes in a full-band-gap ultrasonic crystal. Physical Review B, 68, 214301 (2003) |
| [11] | Khelif, A., Choujaa, A., Benchabane, S., Djafari-Rouhani, B., and Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Applied Pysics Letters, 84, 4400– 4402 (2004) |
| [12] | Lu, T. J., Gao, G. Q., Ma, S. L., Feng, J., and Kim, T. Acoustic band gaps in two-dimensional square arrays of semi-hollow circular cylinders. Science in China Series E: Technological Sciences, 52, 303–312 (2009) |
| [13] | Hu, X. H., Chan, C. T., and Zi., J. Two-dimensional sonic crystals with Helmholtz resonators. Physical Review E, 71, 055601 (2005) |
| [14] | Hsieh, P. F., Wu, T. T., and Sun, J. H. Three-dimensional phononic band gap calculations using the FDTD method and a PC cluster system. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 53, 148–158 (2006) |
| [15] | Su, X. X. and Wang, Y. S. A postprocessing method based on high-resolution spectral estimation for FDTD calculation of phononic band structures. Physica B: Condensed Matter, 405, 2444–2449 (2010) |
| [16] | Axmann, W. and Kuchment, P. An efficient finite element method for computing spectra of photonic and acoustic band-gap materials I: scalar case. Journal of Computational Physics, 150, 468–481 (1999) |
| [17] | Li, J. B., Wang, Y. S., and Zhang, C. Tuning of acoustic band gaps in phononic crystals with Helmholtz resonators. Journal of Vibration and Acoustics, 135(3), 031015 (2013) |
| [18] | Stoica, P. and Moses, R. Spectral Analysis of Signals, Prentice Hall, New Jersey (2005) |
| [19] | Golberg, M. A. and Chen, C. S. The method of fundamental solutions for potential, Helmholtz and diffusion problems. Computational Engineering, WIT Press, Boston, 103–176 (1998) |
| [20] | Chen, W. and Tanaka, M. A meshless, integration-free, and boundary-only RBF technique. Computers and Mathematics with Applications, 43, 379–391 (2002) |
| [21] | Hu, H. Y., Chen, J. S., and Hu, W. Weighted radial basis collocation method for boundary value problems. International Journal for Numerical Methods in Engineering, 69, 2736–2757 (2007) |
| [22] | Sarra, S. A. Adaptive radial basis function methods for time dependent partial differential equations. Applied Numerical Mathematics, 54, 79–94 (2005) |
| [23] | Chen, C. S., Fan, C.M., andWen, P. H. The method of approximate particular solutions for solving certain partial differential equations. Numerical Methods for Partial Differential Equations, 28, 506–522 (2012) |
| [24] | Hart, E. E., Cox, S. J., and Djidjeli, K. Compact RBF meshless methods for photonic crystal modelling. Journal of Computational Physics, 230, 4910–4921 (2011) |
| [25] | Kosec, G. and Sarler, B. Solution of phase change problems by collocation with local pressure correction. Computer Modeling in Engineering and Sciences, 25, 191–216 (2009) |
| [26] | Zheng, H., Zhang, C. Z., Wang, Y. S., Sladek, J., and Sladek, V. A meshfree local RBF collocation method for anti-plane transverse elastic wave propagation analysis in 2D phononic crystals. Journal of Computational Physics, 305, 997–1014 (2016) |
 2016, Vol. 37
2016, Vol. 37





















