Shanghai University
Article Information
- Jincun LIU, Hong LI, Yang LIU, Zhichao FANG. 2016.
- Reduced-order finite element method based on POD for fractional Tricomi-type equation
- Appl. Math. Mech. -Engl. Ed., 37(5): 647-658
- http://dx.doi.org/10.1007/s10483-016-2078-8
Article History
- Received Oct. 9, 2015
- Revised Oct. 16, 2015
Fractional calculus has a history of at least three hundred years. However,it is in the past several decades that the adoption of fractional differential equations (FDEs) for mathematical modeling has attracted great attention and become increasingly popular. Many problems in physics,chemistry,biology,and other fields can be expressed very suitably and successfully by FDEs[1]. Unfortunately,it is difficult to obtain the analytic solutions of many FDEs,and approximate methods should be considered.
At present,some numerical methods have been developed to obtain the approximate solutions for fractional equations. Finite difference (FD) methods were studied in Refs. [2]-[3],a spectral method approximation was proposed by Lin and Xu[4],finite element method (FEM) has also been considered to get the approximate solutions of variational problem for the FDEs[5, 6, 7, 8, 9],and so on. Among these numerical methods,the FEM is more popular because of its flexibility to irregular regions and low requirement for the smoothness of solutions. However,the general FEM always includes many degrees of freedom,especially when we solve high dimensional-space problems. It is well-known that fractional differential operators are nonlocal operators. And for this reason,a common problem,which is brought about by applying the general FEM to solve FDEs,is that high consumption of memory and long time calculation inevitably occur in the computational process. To overcome this difficulty,some authors proposed “fixed memory principle”[1, 10] or “nested mesh concept”[11]. However,these measures are at the cost of certain accuracy with the reduction of memory size. It is worth considering how to choose suitable basis functions for the FEM so that the degree of freedom is decreased, the computing efficiency is improved,and at the same time,the sufficient accurate numerical solutions are guaranteed.
Holmes et al.[12] introduced a POD method in 1996. This method was called the principalcomponent analysis in statistics[13] and the Karhunen-Loeve expansion in pattern recognition[14], which provided us with the means of constructing orthogonal basis to represent the given data by the least squares optimal sense. Some numerical methods combining with the POD theory for partial differential equations can effectively establish reduced-order models,thereby reducing the size of memory and accelerating computational speed. For example,Kunisch and Volkwein[15, 16] presented the method,which combined the Galerkin projection with the POD theory,to solve the parabolic problem and equations in fluid dynamics. Sun et al.[17],Luo et al.[18, 19],and Luo[20] have presented reduced-order FD methods,reduced-order finite element (FE) schemes,and reduced-order finite volume element formulations based on the POD as well as error estimates for some equations,all of which have obtained good effects. Until this day, we have not seen any other published papers of addressing to the FEM based on the POD for FDEs except Ref. [21]. In this paper,we introduce the reduced-order FEM based on the POD technique to solve the following time-fractional Tricomi-type equation:
Here,Dαt u is the αth-order Caputo fractional derivative,and 1 < α < 2,which is defined by Here,Γ(·) denotes the Gamma function,and γ is a real non-negative constant. Ω ⊂ R2 is a bounded and polygonal domain with the boundary ∂Ω. The operator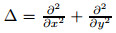 denotes
the Laplacian operator with respect to space variables.
For Eq. (1),the classical FEM,which is based on the FE formulation for the space and
the FD for the time,was considered in Ref. [9]. Its FE scheme shows that,to obtain the
solution at the time tn,the former all solutions on time levels t1,t2,· · · ,tn−1 are needed.
Therefore,the memory requirement for computer has to be enlarged. What’s more,the use of
traditional basis functions for the FEM leads to solve algebraic equations with a large number
of unknown quantities,which requires long time to complete calculation. In this paper,d POD
basis functions are constructed and adopted,where d is only the number of the first few maximal
eigenvalues of matrix KQ×Q (see Section 2). On every time level,only d unknown quantities are
to be solved. Therefore,the degrees of freedom are reduced,and the computing time is cut down
drastically. It should be noted that we construct the POD basis by snapshots which is taken
from the solutions of former Q time levels in the general FEM,while for practical problems in
the scientific research,we can get the snapshots by drawing samples from experiments or by
the past data information.
denotes
the Laplacian operator with respect to space variables.
For Eq. (1),the classical FEM,which is based on the FE formulation for the space and
the FD for the time,was considered in Ref. [9]. Its FE scheme shows that,to obtain the
solution at the time tn,the former all solutions on time levels t1,t2,· · · ,tn−1 are needed.
Therefore,the memory requirement for computer has to be enlarged. What’s more,the use of
traditional basis functions for the FEM leads to solve algebraic equations with a large number
of unknown quantities,which requires long time to complete calculation. In this paper,d POD
basis functions are constructed and adopted,where d is only the number of the first few maximal
eigenvalues of matrix KQ×Q (see Section 2). On every time level,only d unknown quantities are
to be solved. Therefore,the degrees of freedom are reduced,and the computing time is cut down
drastically. It should be noted that we construct the POD basis by snapshots which is taken
from the solutions of former Q time levels in the general FEM,while for practical problems in
the scientific research,we can get the snapshots by drawing samples from experiments or by
the past data information.
The plan of this paper is as follows. In Section 2,we first recall the fully-discrete general FE formulation for the time-fractional Tricomi-type equation,then,introduce the POD method and establish the reduced-order FE scheme based on the POD. In Section 3,the stability and error estimate for the reduced-order FE solution are proved particularly. The implementation process of the method is presented in Section 4. Two numerical examples are shown in Section 5 to demonstrate that the numerical results are consistent with the theoretical analysis.
2 Establishment of reduced-order FEMThe Sobolev space used as follows is standard (see Ref. [22]). Let (·,·) represent the L2 inner product,and its corresponding L2 norm is denoted by || · ||. We denote by || · ||r the norm in Hr(Ω).
2.1 Recall general FE schemeWe first partition the time interval [0,T] by ti (i = 0,1,· · · ,N),where 0 = t0 < t1 < · · · <
tN = T ,tn = nk (n = 1,2,· · · ,N),and  . Then,for a fixed n,the Caputo fractional
derivative (2) is approximated as follows[7]:
. Then,for a fixed n,the Caputo fractional
derivative (2) is approximated as follows[7]:

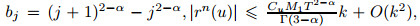 ,Cu denotes a constant which
is relevant to u,and M1 is the upper bound of
,Cu denotes a constant which
is relevant to u,and M1 is the upper bound of 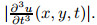 . When j = 1,u(t−1) can be
approximated by u(0) − kut(0) = φ0 − kφ1,where t−1 = −k.
. When j = 1,u(t−1) can be
approximated by u(0) − kut(0) = φ0 − kφ1,where t−1 = −k.
We can verify easily that bj have the following properties:
Let  be a quasi-uniform triangle subdivision to the space region Ω. The maximal
length of the sides of the triangulations is denoted by h. Let Sh ⊂ H0 1(Ω) be a kind of FE
space,and its degree of accuracy is not lower than one,i.e.,
be a quasi-uniform triangle subdivision to the space region Ω. The maximal
length of the sides of the triangulations is denoted by h. Let Sh ⊂ H0 1(Ω) be a kind of FE
space,and its degree of accuracy is not lower than one,i.e.,

Let uh−1 and uhn denote the approximations to u(x,y,t−1) and u(x,y,tn),respectively. Set f n = f(x,y,tn). Then,the fully-discrete formulation of (1) can be stated as following.
To get the approximate solution uhn ∈ Sh (1 ≤ n ≤ N),
holds for any vh ∈ Sh,where γ0 = (nk)2γ,and α0 = kαΓ(3 − α). u0 h may be taken as P φ0, where P is the L2 projection operator that satisfies (P u − u,v) = 0,∀v ∈ Pr(Ω),and uh−1 can be taken as P(φ0 − kφ1),or else.The stability of problem (4) is proved in Ref. [9],and the following error estimate is presented.
Lemma 1[9] Let un = u(x,y,tn) be the exact solution of (1) and uhn be the finite element approximate solution of the fully-discrete formulation (4). Assume that un satisfy utn ∈ L2(0,T ; Hr+1(Ω)) ∩ L∞(0,T ; Hr+1(Ω)),uttn ∈ L2(0,T ; L2(Ω)),with φ0,φ1 ∈ Hr+1(Ω). Then, uhn satisfies the following error estimates:

Suppose that we have got the snapshots Ui (i = 1,2,· · · ,Q),at least one of which is assumed to be non-zero. Let

Definition 1[18] The POD method is to find the orthogonal basis ηk (k = 1,2,· · · ,q) which satisfies that for each d (1 ≤ d ≤ q),the mean square error is minimum on the average, that is,
subject to where ||Ui||X = ||▽Ui||. A solution set {ηk}k=1d of (6) and (7) is called a POD basis of rank d.Introduce a matrix K = (Kij)Q×Q associated with the snapshots {Ui}i=1Q by

Lemma 2[15, 16] Let λ1 ≥ λ2 ≥ · · · ≥ λq > 0 denote the positive eigenvalues of matrix K,and ω1,ω2,· · · ,ωq are the associated orthogonal eigenvectors. Then,a POD basis of rank d ≤ q is expressed by


We first take uhi (i = 1,2,· · · ,Q,Q << N),which are the solutions of (4),as the snapshots for convenience. Let Sd = span{η1,η2,· · · ,ηd} (1 ≤ d ≤ q). Define the Ritz-projection P d : Sh → Sd denoted by
From the linear operator theory,there exists a unique extension P h : H0 1 → Sh of P d such that P h|Sh = P d : Sh → Sd defined by where u ∈ H1 0(Ω). If u ∈ H s(Ω),there holds the following estimates (see Ref. [23]):
Lemma 3[18] For each d (1 ≤ d ≤ q),it holds the following estimates for projection operator P d :

Now the reduced-order FEM based on the POD theory for Eq. (1) can be stated as follows.
Find udn ∈ Sd (n = 1,2,· · · ,N) such that for any vd ∈ Sd,
Here,uhn (n = 1,2,· · · ,Q) are chosen from the first Q solutions of (4).Since (udn ,vd) + α0(▽udn ,▽vd) is positive definite,the problem (13) has a unique solution udn ∈ Sd.
Remark 1 We construct the POD basis by snapshots which are taken from the solutions of
former Q time levels in the general FEM. However,the snapshots can be obtained by drawing
samples from experiments or by the past data information for practical problems. Suppose
that we take Sh as the piecewise linear functions space,that is r = 1 in Sh. If we use the FE
scheme (13) to solve the approximate solution of Eq. (1),the number of unknown quantities
equals to the amount of inner vertices of triangles in  (see Ref. [23]). While if we solve the
equation by reduced-order FE scheme (13),the amount of total degrees of freedom is only
d (d ≤ q ≤ Q << N ),where d is just the number of former bigger positive eigenvalues of matrix
KQ×Q. Therefore,it is tiny (see the numerical example in Section 5). On the other hand,we
have found from the discrete formulations (4) and (13) that the solutions of all former time
levels which satisfy t < tn must be saved and added up in order to get the solution at the time
tn. Consequently,when we solve the numerical solution of Eq. (1) by applying reduced-order
FE scheme (13),its computational quantities are largely decreased since the degrees of freedom
in each time level are much less than those by using the classic FE formulation.
(see Ref. [23]). While if we solve the
equation by reduced-order FE scheme (13),the amount of total degrees of freedom is only
d (d ≤ q ≤ Q << N ),where d is just the number of former bigger positive eigenvalues of matrix
KQ×Q. Therefore,it is tiny (see the numerical example in Section 5). On the other hand,we
have found from the discrete formulations (4) and (13) that the solutions of all former time
levels which satisfy t < tn must be saved and added up in order to get the solution at the time
tn. Consequently,when we solve the numerical solution of Eq. (1) by applying reduced-order
FE scheme (13),its computational quantities are largely decreased since the degrees of freedom
in each time level are much less than those by using the classic FE formulation.
In this section,we develop stability analysis as well as the error estimate for the problem (13). From here,we will denote a generic constant by C,which may not be the same at different positions,but it is always independent of the steps k and h. For convenience and without lose of generality,we assume that φ0(x,y) and φ1(x,y) are two zero functions in the following stability analysis.
Theorem 1 The reduced-order FE scheme (13) has a unique solution udn ∈ Sd which satisfies the following stability result:
Let uhn and udn be the solutions of problem (4) and problem (13),respectively. If k = O(h),and Q = O(N 1/2),it holds the error estimate
Proof Take vd = udn in (13),we can get


In the following,we apply the mathematical induction method to prove the result (14). In fact,when n = 1,it is obvious that



In order to carry out the error estimate,we subtract (13) from (4) and get the error equation
According to (8) and (15),we get

By the Hölder inequality and (10),we obtain that when k = O(h),

Therefore,
Setting Q = O(N 1/2) and using triangle inequality,(16),(11),and (12),we have

Once again,we can derive the following estimate by the mathematical induction method:

Since it is similar to the above proof,we omit the process.
According to the triangle inequality and the estimate results in Lemma 1 and Theorem 1, the error between the exact solution and reduced-order solution can be easily obtained.
Theorem 2 Let un = u(tn) and udn be the solutions of the problem (1) and (13),respectively. Assume un satisfying utn ∈ L2(0,T ; Hr+1(Ω)) ∩ L∞(0,T ; Hr+1(Ω)) and uttn ∈ L2(0,T ; L2(Ω)). If k = O(h),Q = O(N 1/2),there holds the following error estimate for n = 1,2,· · · ,Q,Q + 1,· · · ,N:

Remark 2 The condition Q = O(N 1/2) in Theorem 1 and Theorem 2 shows that only the
solutions on the former Q time levels of the general FE scheme need to be taken as snapshots.
The condition k = O(h) in theorems is just an assumption for the theoretical analysis. It can
be changed properly on other cases. The error estimate results in two theorems also provide a
measurement for deciding the number of POD basis,that is,the number d of POD basis should
satisfy 
In this section,we give the implementation process for solving the problem (13),which can be divided into six steps.
Step 1 Solve the equation (4) for given f(x,y,t) when n = 1,2,· · · ,Q and obtain the snapshots Ui(x,y) = uhi (i = 1,2,· · · ,Q).
Step 2 Compute the matrix K = (Kij)Q×Q,where  .
.
Step 3 Solve the rank q and eigenvalues of matrix K and obtain eigenvalues λ1 ≥ λ2 ≥ · · · ≥ λq > 0. The associated orthogonal eigenvectors ω1,ω2,· · · ,ωq also need to be solved out.
Step 4 Choose the number d ≤ q such that the following inequality is satisfied

Then,the POD basis is generated,i.e.,
Step 5 Set Sd = span{η1(x,y),η2(x,y),· · · ,ηd(x,y)},solve Eq. (13) with only d degrees of freedom,and get its solution udn (n = 1,2,· · · ,N).
Step 6 For given error  ,udn is the
solution of the problem (13),else let Ui = udi (i = n − Q,n − Q + 1,· · · ,n − 1),and repeat Step
1 to Step 5.
,udn is the
solution of the problem (13),else let Ui = udi (i = n − Q,n − Q + 1,· · · ,n − 1),and repeat Step
1 to Step 5.
In this section,we provide two numerical examples to verify our theoretical analysis results
further. Assume that  is a triangular partition to the region [0,1] × [0,1],and Sh is the space
of piecewise linear and continuous functions,which means that we all take r = 1 in the following
examples. Let
is a triangular partition to the region [0,1] × [0,1],and Sh is the space
of piecewise linear and continuous functions,which means that we all take r = 1 in the following
examples. Let  and
and  .
.
Example 1 Consider the following problem in the two-dimensional space:

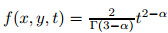 sin(2πx) sin(2πy) + 8π2t3 sin(2πx) sin(2πy). The exact solution of
this equation is u(x,y,t) = t2 sin(2πx) sin(2πy).
sin(2πx) sin(2πy) + 8π2t3 sin(2πx) sin(2πy). The exact solution of
this equation is u(x,y,t) = t2 sin(2πx) sin(2πy).
The error estimate results when T = 1 are listed in Table 1 for different α,M,N,and Q,but d = 2 is only needed. Under the condition k = O(h) and Q = O(N 1/2),we find that the convergent accuracy in the L2 norm for the reduced-order FE solution solved by the formulation (13) almost arrives at second-order for different values of α. The influence of space is obvious since our problem is two-dimensional in space. Although we only adopt d = 2 POD basis functions,high accuracy is still obtained,and meanwhile,the calculation quantities and computer memory are both saved.
Next,we choose another example to show the efficiency of the reduced-order FEM. To this end,we solve the following equation by formulas (4) and (13),respectively.
Example 2
We take the source term
Then,the exact solution of equation (17) is
For α = 1.5,we obtain the approximate solution when T = 2. The FE solution uh and
reduced-order FE solution ud are displayed in Fig. 1,and their error maps with the exact solution
are exhibited in Fig. 2. In these computational process,we take M = 64,N = 200,Q = 15,
which satisfies Q = O(N 1/2),k = O(h). d is set to be 6 since it should satisfy d ≤ q and  . We can see from the figures that the reducedorder FE solution is still convergent without renewing the POD basis and has the similar effect
with the FE solution. In computing time,the classical FE formulation (4),which includes
64 × 64 degrees of freedom on every time level,the required time of solving system of equations
is 8 min,while for the reduced-order FEM (13) with 6 POD basis functions,the corresponding
time is only 2 s. That means,to solve Eq. (17),the required time of solving equations by the
classical FE formulation (4) is 240 times that of the reduced-order FEM based on the POD
with only 6 degrees of freedom on every time level. Although the construction of POD basis
functions also consumes time,it is much less than that computed by the standard FEM in the
whole process since Q = O(N 1/2).
. We can see from the figures that the reducedorder FE solution is still convergent without renewing the POD basis and has the similar effect
with the FE solution. In computing time,the classical FE formulation (4),which includes
64 × 64 degrees of freedom on every time level,the required time of solving system of equations
is 8 min,while for the reduced-order FEM (13) with 6 POD basis functions,the corresponding
time is only 2 s. That means,to solve Eq. (17),the required time of solving equations by the
classical FE formulation (4) is 240 times that of the reduced-order FEM based on the POD
with only 6 degrees of freedom on every time level. Although the construction of POD basis
functions also consumes time,it is much less than that computed by the standard FEM in the
whole process since Q = O(N 1/2).
 |
| Fig. 1 FE solution uh and reduced-order FE solution ud when T = 2, α = 1.5 |
 |
| Fig. 2 Error charts of u − uh and u − ud when T = 2 and α = 1.5 |
| [1] | Podlubny, I. Fractional Differential Equations, Academic Press, New York (1999) |
| [2] | Liu, F., Anh, V., Turner, I., and Zhang, P. Time fractional advection dispersion equation. Journal of Applied Mathematics and Computing, 13(1), 233–245 (2003) |
| [3] | Yuste, S. B. and Acedo, L. An explicit finite difference method and a new von Numann-type stability analysis for fractional diffusion equation. SIAM Journal on Numerical Analysis, 42(5), 1862–1874 (2005) |
| [4] | Lin, Y. M. and Xu, C. J. Finite difference/spectral approximations for the time-fractional diffusion equation. Journal of Computational Physics, 225(2), 1533–1552 (2007) |
| [5] | Ervin, V. J. and Roop, J. P. Variational formulation for the stationary fractional advection dispersion equation. Numerical Methods for Partial Differential Equations, 22(3), 558–576 (2006) |
| [6] | Zhang, H., Liu, F., and Anh, V. Galerkin finite element approximations of symmetric spacefractional partial differnetial equations. Applied Mathematics and Computation, 217(6), 2534– 2545 (2010) |
| [7] | Li, C. P., Zhao, Z. G., and Chen, Y. Q. Numerical approximation of nonlinear fractional differential equations with subdiffusion and superdiffusion. Computers and Mathematics with Applications, 62(3), 855–875 (2011) |
| [8] | Ford, N. J., Xiao, J. Y., and Yan, Y. B. A finite element method for time fractional partial differential equations. Fractional Calculus and Applied Analysis, 14(3), 454–474 (2011) |
| [9] | Zhang, X. D., Huang, P. Z., Feng, X. L., andWei, L. L. Finite element method for two-dimensional time-fractional Tricomi-type equations. Numerical Methods for Partial Differential Equations, 29(4), 1081–1096 (2013) |
| [10] | Deng, W. H. Short memory principle and a predictor-corrector approach for fractional differential equations. Journal of Computational and Applied Mathematics, 206(1), 174–188 (2007) |
| [11] | Ford, N. J. and Simpson, A. C. The numerical solution of fractional differential equations: speed versus accuracy. Numerical Algorithms, 26(4), 333–346 (2001) |
| [12] | Holmes, P. J., Lumley, L., and Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge University Press, Cambridge (1996) |
| [13] | Jolliffe, I. T. Principal Component Analysis, Springer-Verlag, Berlin (2002) |
| [14] | Fukunaga, K. Introduction to Statistical Pattern Recognition, Academic Press, New York (1990) |
| [15] | Kunisch, K. and Volkwein, S. Galerkin proper orthogonal decomposition methods for parabolic problems. Numerische Mathematik, 90(1), 117–148 (2001) |
| [16] | Kunisch, K. and Volkwein, S. Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics. SIAM Journal on Numerical Analysis, 40(2), 492–515 (2002) |
| [17] | Sun, P., Luo, Z. D., and Zhou, Y. J. Some reduced finite difference schemes based on a proper orthogonal decomposition technique for parabolic equations. Applied Numerical Mathematics, 60, 154–164 (2010) |
| [18] | Luo, Z. D., Chen, J., Sun, P., and Yang, X. Z. Finite element formulation based on proper orthogonal decomposition for parabolic equations. Science in China Series A: Mathematics, 52(3), 585–596 (2009) |
| [19] | Luo, Z. D., Li, H., Zhou, Y. J., and Huang, X. M. A reduced-order FVE formulation based on POD method and error analysis for two-dimensional viscoelastic problem. Journal of Mathematical Analysis and Applications, 385(1), 310–321 (2012) |
| [20] | Luo, Z. D. A reduced-order SMFVE extrapolation algorithm based on POD technique and CN method for the non-stationary Navier-Stokes equations. Discrete and Continuous Dynamical Systems Series B, 20(4), 1189–1212 (2015) |
| [21] | Liu, J. C., Li, H., Fang, Z. C., and Liu, Y. Application of low-dimensional finite element method to fractional diffusion equation. International Journal of Modeling, Simulation, and Scientific Computing, 5(4), 1450022 (2014) |
| [22] | Adams, R. A. Sobolev Spaces, Academic Press, New York (1975) |
| [23] | Thomée, V. Galerkin Finite Element Methods for Parabolic Problems, Springer-Verlag, Berlin (1997) |
 2016, Vol. 37
2016, Vol. 37




















