Shanghai University
Article Information
- Dawei LI, Zongzan LI, Yicheng SONG, Junqian ZHANG. 2016.
- Analysis of diffusion induced elastoplastic bending of bilayer lithium-ion battery electrodes
- Appl. Math. Mech. -Engl. Ed., 37(5): 659-670
- http://dx.doi.org/10.1007/s10483-016-2079-8
Article History
- Received May 7, 2015
- Revised Oct. 30, 2015
2. Department of Mechanics, College of Sciences, Shanghai University, Shanghai 200444, China;
3. Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai 200072, China
Lithium-ion battery has quickly become research focus in recent years due to its advantages of high power density,high energy capacity,low self-discharge rate,and environmental friendliness in the applications from portable electric devices to electric vehicles[1, 2]. The electrode of lithium-ion battery usually employs a layered structure which is composed of active materials such as graphite,silicon or LiCoO2,and current collector made of copper or aluminum. Bilayer electrode,which is composed of one active layer and one current collector layer,is widely used due to its easily manufactured simple structure. During cell charging,the lithiation induced deformation of active layer is restricted by current collector,leading to bending of the bilayer electrode[3, 4]. In our on-going experimental study,the bilayer electrode is proposed for in-situ measurement of diffusion induced deformation and stress. In this paper,we will carry out the theoretical analysis which can be considered as the theoretical base for the experimental design and data analysis in the experimental study.
Among the large amount of studies devoted to the diffusion induced deformation[3, 4, 5, 6, 7],the current collector was customarily considered as an elastic material. Although the plastic yield of active material has been widely discussed[8, 9, 10, 11, 12, 13, 14, 15],the plastic yield of current collector has been rarely investigated. This is probably because of the traditional belief that the plastic deformation in mechanical design should be avoided. In our recent work,a strategy to reduce the diffusion induced stress and to enhance the capacity of a layered electrode by allowing the plastic deformation of current collector has been proposed[16]. Furthermore,the current collector might be plastically yielded during charge operations because it is usually very thin in cells. Therefore,a systematic analysis is demanded for the bending of bilayer electrode with consideration of plastic yield of current collector.
In this paper,an elastoplastic analysis which accounts for plastic yield of current collector will be formulated for the diffusion induced bending of bilayer electrodes. The parameters that influence the elastoplastic bending will be identified. The potential application of the obtained analytical solution will be addressed.
2 Diffusion induced elastoplastic bending of bilayer electrodesConsider a bilayer electrode shown in Fig. 1(a),which is obtained by bonding an active layer to a current collector,where h1 and hc denote the thickness of active layer and current collector,respectively. Usually,the active layer is a composite of active particles,binder,and pores in real batteries. The main function of the binder is to hold the active particles together and to provide passageway for electron transportation. During charge/discharge,lithium-ions are inserted into or extracted out of active particles across the interface between particle and electrolyte in pores,leading to expansion and contraction of active particles. We assume that the composite active layer is macroscopically homogeneous and isotropic in the present study since the focus here is the deformation of whole electrode.
 |
| Fig. 1 Schematic illustration of bilayer electrode |
In the charging process,lithium-ions continuously go into the active material and cause the active layer to expand,while the diffusion-induced expansion is restricted by the current collector. The deformation mismatch makes the electrode bend,as shown in Fig. 1(b). Let the thickness direction be aligned with the z-axis and the in-plane of plate with the x- and y-axes. According to the small deformation theory,it was shown in Ref. [3] that the stress and strain components associated with the thickness direction are all zero,and the in-plane normal strain in the x-axis can be expressed as
where ε0 is the strain at the plane z = 0 characterizing the elongation strain of the electrode, and κ is the curvature. This equation suggests that the active layer and current collector are bonded well and have the same bending curvature.
The common active particle materials such as graphite and LiFePO4 do not show significant plastic deformation behaviors during cell charging. Therefore,the elastic macroscopic constitutive equation of the composite active layer incorporating diffusion induced deformation can be expressed as follows:
where E1 and ν1 are Young’s modulus and Poisson’s ratio of the composite,respectively,and c is the molar concentration defined as the total number of moles of ions in active particles per unit volume of the composite. Ω is the partial molar volume representing the volume change due to the unit concentration. Ωc in Eq. (2a) represents the volumetric strain of composite due to insertion of lithium-ions. Upon lithiation,it is common that the elastic properties of an active material vary with lithium-ion concentration. For example,the graphite becomes stiffer while the silicon softens with lithiation[17]. Therefore,E1,ν1,and Ω may depend upon the concentration,in turn,are implicit functions of z.
The current collector in batteries is usually made of copper or aluminum,which may be plastically yielded in charging process. Assuming that the current collector is an elastoplastic material with linear strain hardening behavior,the elastoplastic constitutive is illustrated in Fig. 2 and provided as follows:
 |
| Fig. 2 Illustration of plastic constitutive behavior of current collector |
Assume that the bilayer is free of mechanical constraint,and the total mechanical balance implies
During lithiation,the current collector is stretched and bended due to the expansion of active materials. According to the development of plastic deformation in the current collector and using hp to denote the thickness of plastic region in the current collector,as shown in Fig. 1(b), the whole charge duration can be divided into three stages: i.e.,the elastic stage when hp = 0, partially plastic stage when 0 < hp < hc,and the fully plastic stage when hp = hc.
2.1 Elastic stage (hp = 0)Both active layer and current collector layer in the bilayer electrode undergo elastic bending before the state of charge (SOC) reaches a critical value when the stress in the current collector satisfies the yield condition. By substituting Eqs. (2a) and (3b) into Eqs.(4a) and (4b),one can obtain the in-plane strain and curvature of bilayer electrode as follows:
where A,B,and I are the extensional stiffness,the stretching-bending coupling stiffness,and the bending stiffness,respectively,and N c and M c are the concentration force resultant and the concentration moment resultant,respectively. They are written as In order to use Eqs. (5a) and (5b) to evaluate the in-plane strain and curvature of elastic bending of bilayer electrode,the lithium-ion concentration distribution has to be known. Generally,the concentration is not uniform spatially and may vary from location to location,and therefore, should be obtained by solving the diffusion model[18].For the active layer which is a composite of active particles,binder and pores,all active particles are soaked in electrolyte. If the active layer is thin,it might be considered that lithium-ions migrate into all active particles in the layer at the same time. Therefore,it could be assumed that the concentration,c,is macroscopically uniform across the layer. In this case, the elastic modulus of active layer does not vary with the thickness coordinate,and the explicit expressions for the in-plane strain and bending curvature can be derived as follows:
where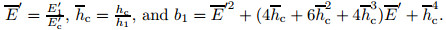 2.2 Elastoplastic stage (0 < hp < hc)
2.2 Elastoplastic stage (0 < hp < hc)
With the development of lithiation,the current collector will be stretched and be partially plastically yielded. Considering the yield criterion σc = σY,the location of the elastic-plastic interface can be determined via
There are two interfaces in this stage. One is the interface between the active layer and the current collector denoted by z = 0,and the other is the elastic-plastic interface in the current collector at the location z =−hp. Divided by these two interfaces,the whole electrode is partitioned into three regions. The stress in the active layer is still described by Eq. (2a). The stress in the current collector can be expressed as follows by using Eqs. (1) and (3a)−(3c):
where α = 1/(1 + Ep ' /Ec ') is a dimensionless parameter. Substituting the stresses in the three regions given by Eqs. (2a) and (10) into the total balance conditions,Eqs. (4a) and (4b),gives Solving it for ε0 and κ leads to where
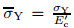 is the normalized yield stress of current collector.
is the normalized yield stress of current collector. 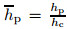 is the normalized
thickness of plastic region and is yet to be determined by the yield condition. By substituting
Eqs. (12a) and (12b) into the yield condition (9),we obtain the equation for determination of
elastic-plastic boundary as follow:
is the normalized
thickness of plastic region and is yet to be determined by the yield condition. By substituting
Eqs. (12a) and (12b) into the yield condition (9),we obtain the equation for determination of
elastic-plastic boundary as follow:
If the distribution of lithium-ion concentration c in the bilayer electrode is known,which,
for example,could be obtained by solving the diffusion equation[18], ,and
,and  can be evaluated,and the thickness of plastic layer
can be evaluated,and the thickness of plastic layer  ,which should lie in the interval
,which should lie in the interval  ,
is easily obtained from Eq. (13). By substituting the obtained
,
is easily obtained from Eq. (13). By substituting the obtained  back into Eqs. (12a) and
(12b),one can evaluate the in-plane strain ε0 and bending curvature κ of a bilayer electrode.
From Eq. (13),it is inferred that the thickness of plastic layer
back into Eqs. (12a) and
(12b),one can evaluate the in-plane strain ε0 and bending curvature κ of a bilayer electrode.
From Eq. (13),it is inferred that the thickness of plastic layer  has five influence parameters,
i.e.,the thickness ratio
has five influence parameters,
i.e.,the thickness ratio  ,the dimensionless yield stress
,the dimensionless yield stress  ,the elastic modulus ratio
,the elastic modulus ratio  ,the dimensionless plastic modulus
,the dimensionless plastic modulus  ,and the partial molar volume Ω. Furthermore,such five
parameters are also the influence parameters of the in-plane strain and bending curvature.
,and the partial molar volume Ω. Furthermore,such five
parameters are also the influence parameters of the in-plane strain and bending curvature.
Again,for a composite active layer where the macroscopically uniform distribution of concentration across the layer could be assumed, ,and
,and  in Eq. (13) can be explicitly
expressed,and the equation for thickness of plastic layer can be reduced to
in Eq. (13) can be explicitly
expressed,and the equation for thickness of plastic layer can be reduced to
The analytical elastoplastic solutions given by Eqs. (14a)-(15b) for the uniform lithiation explicitly show that the in-plane strain and bending curvature of bilayer electrode depend upon five dimensionless parameters,i.e.,the thickness ratio  ,the dimensionless yield stress σY,
the elastic modulus ratio
,the dimensionless yield stress σY,
the elastic modulus ratio  ,the dimensionless plastic modulus E'p/Ec ',and the partial molar
volume Ω.
,the dimensionless plastic modulus E'p/Ec ',and the partial molar
volume Ω.
The role of concentration-dependent elastic properties on bending is reflected by the elastic
modulus ratio  . In order to illustrate the combined response in calculation,we use a simple
linear relation of the elastic modulus versus lithium-ion concentration[17],
. In order to illustrate the combined response in calculation,we use a simple
linear relation of the elastic modulus versus lithium-ion concentration[17],
In fully plastic stage,the whole current collector can be plastically yielded,in another word,
 = 1. Therefore,the lithiation induced deformation,characterized by the in-plane strain ε0
and bending curvature κ,can be simply obtained by introducing
= 1. Therefore,the lithiation induced deformation,characterized by the in-plane strain ε0
and bending curvature κ,can be simply obtained by introducing  = 1 into Eqs. (15a) and
(15b).
= 1 into Eqs. (15a) and
(15b).
For illustration,we will consider graphite-particulate composites as the active layer in bilayer electrodes where the lithium-ions are inserted into all active particles simultaneously. Therefore, lithium-ion concentration c in the composite can be assumed to be uniform across thickness, and thereby,the SOC is equal to c/cmax. The partial molar volume Ω = 2.0 × 10−6 m3/mol and the constant k in Eq. (16),k = 3,are assumed[17].
In Figs. 3(a)−6(c),we plot the thickness of plastic layer,the in-plane strain,and the bending
curvature as a function of SOC in order to show the elastoplastic bending progression with
lithiation,as well as effects of four dimensionless parameters,i.e.,the initial modulus ratio
 ,the thickness ratio
,the thickness ratio  ,the dimensionless yield stress σY,and the dimensionless
plastic modulus E'p/Ec '. In the charging process,the active materials expand due to lithiumions insertion,while the current collector suppresses this deformation. Therefore,the tensile
stress is generated in the current collector. In the first stage where the deformation is elastic,
the in-plane strain and the bending curvature take a quick increase. As the lithiation goes on,
the current collector starts to be yielded plastically from the interface of electrode where the
tensile stress in the current collector takes a maximum value. The plastic region extends from
the interface toward interior of current collector and finally spans over the whole thickness of
current collector as the lithiation continues. In this elastoplastic stage,the in-plane strain and
the bending curvature continue to increase as the intercalation goes on,however,the increase
rates slow down.
,the dimensionless yield stress σY,and the dimensionless
plastic modulus E'p/Ec '. In the charging process,the active materials expand due to lithiumions insertion,while the current collector suppresses this deformation. Therefore,the tensile
stress is generated in the current collector. In the first stage where the deformation is elastic,
the in-plane strain and the bending curvature take a quick increase. As the lithiation goes on,
the current collector starts to be yielded plastically from the interface of electrode where the
tensile stress in the current collector takes a maximum value. The plastic region extends from
the interface toward interior of current collector and finally spans over the whole thickness of
current collector as the lithiation continues. In this elastoplastic stage,the in-plane strain and
the bending curvature continue to increase as the intercalation goes on,however,the increase
rates slow down.
 |
Fig. 3 Variation of (a) thickness of plastic layer, (b) in-plane strain, and (c) curvature as function of
SOC with different thickness ratios  |
 |
Fig. 4 Variation of (a) thickness of plastic layer, (b) in-plane strain, and (c) curvature as function of
SOC with different modulus ratio  |
 |
Fig. 5 Variation of (a) thickness of plastic layer, (b) in-plane strain, and (c) curvature as function of
SOC with different normalized yield stresses  |
 |
| Fig. 6 Variation of (a) thickness of plastic layer, (b) in-plane strain, and (c) curvature as function of SOC with different dimensionless plastic moduli Ep'/Ec' |
Figures 3(a)−3(c) illustrate the effects of the thickness ratio of current collector to active
layer, ,on the variation of thickness of plastic layer,in-plane strain and curvature
against the SOC. It is found that the plastic yield occurs earlier and grows faster in the bilayer
electrode with the smaller thickness ratio. This is because the force induced by expansion of
active layer must be balanced by the relative thinner current collector,resulting in a higher
stress in the current collector. The smaller thickness ratio
,on the variation of thickness of plastic layer,in-plane strain and curvature
against the SOC. It is found that the plastic yield occurs earlier and grows faster in the bilayer
electrode with the smaller thickness ratio. This is because the force induced by expansion of
active layer must be balanced by the relative thinner current collector,resulting in a higher
stress in the current collector. The smaller thickness ratio  makes the in-plane strain larger for
the whole charge process. However,it produces much smaller bending curvature. The relative
thinner current collector can be elongated more with the same diffusion induced load,and help
reduce the restriction between the two layers,and thereby reduce the curvature in the whole
electrode with uniform lithiation.
makes the in-plane strain larger for
the whole charge process. However,it produces much smaller bending curvature. The relative
thinner current collector can be elongated more with the same diffusion induced load,and help
reduce the restriction between the two layers,and thereby reduce the curvature in the whole
electrode with uniform lithiation.
Figures 4(a)−4(c) show impacts of the initial modulus ratio of active layer to current collector  on the variation of
on the variation of  ,ε0,and κ against the SOC. It is seen from Fig. 4(a) that
the small initial modulus ratio,which means employment of soft active layer or stiff current
collector,can delay the plastic yield and makes growth of plastic zone slower. This is easy
to understand since the softer active layer produces smaller load which needs to be balanced
by the stress in the current collector. As it is more difficult for the soft active layer to bring
the current collector to be elongated,the in-plane strain of electrode with the smaller initial
modulus ratio
,ε0,and κ against the SOC. It is seen from Fig. 4(a) that
the small initial modulus ratio,which means employment of soft active layer or stiff current
collector,can delay the plastic yield and makes growth of plastic zone slower. This is easy
to understand since the softer active layer produces smaller load which needs to be balanced
by the stress in the current collector. As it is more difficult for the soft active layer to bring
the current collector to be elongated,the in-plane strain of electrode with the smaller initial
modulus ratio  is smaller,as indicated in Fig. 4(b). In contrast,the curvature of bilayer
electrode with the larger initial modulus ratio
is smaller,as indicated in Fig. 4(b). In contrast,the curvature of bilayer
electrode with the larger initial modulus ratio  is smaller. The reason is that a stiffer active
layer,which expands uniformly,has stronger ability to bring the current collector in bilayer
electrode to deform less inhomogeneously,and thereby results in a smaller bending curvature.
is smaller. The reason is that a stiffer active
layer,which expands uniformly,has stronger ability to bring the current collector in bilayer
electrode to deform less inhomogeneously,and thereby results in a smaller bending curvature.
Effects of the normalized yield stress  on elastoplastic bending behaviors of bilayer
electrode are shown in Figs. 5(a)-5(c). Initiation of plasticity takes place later (higher SOC),as
expected,in the current collector with a higher yield stress. However,influence of yield stress
on the growth rate of plasticity zone is invisible. This delayed plasticity by a higher yield stress
leads to the stress relaxation delayed,and makes the in-plane strain of the electrode smaller
and the bending curvature larger for a given SOC.
on elastoplastic bending behaviors of bilayer
electrode are shown in Figs. 5(a)-5(c). Initiation of plasticity takes place later (higher SOC),as
expected,in the current collector with a higher yield stress. However,influence of yield stress
on the growth rate of plasticity zone is invisible. This delayed plasticity by a higher yield stress
leads to the stress relaxation delayed,and makes the in-plane strain of the electrode smaller
and the bending curvature larger for a given SOC.
Effects of the strain hardening of current collector,characterized by the dimensionless plastic modulus E'p/Ec ',on the elastoplastic bending behaviors of bilayer electrode are illustrated in Figs. 6(a)-6(c). The strain hardening has no effect on initiation of plasticity,and influences slightly the growth rate of plasticity zone. Specifically speaking,the smaller plastic modulus makes growth of plastic zone faster at the stage near the full plasticity. In Fig. 6(b),it is seen that for a given SOC,the larger in-plane strain is associated with the smaller plastic modulus. This is because a smaller plastic modulus releases,to a higher degree,the restraint of the yielded current collector imposed on active layer. In contrast,the bending curvature is lowered by reducing the plastic modulus for a given SOC. The reason is that the uniform expansion of active layer is altered,to a less extent,by the yielded current collector with a smaller plastic modulus,and leads to a smaller bending curvature.
4 ConclusionsIn this paper,an elastoplastic analysis on the lithiation induced deformation of a bilayer electrode has been performed,with consideration of the impacts of plastic yield of current collector. Developments of plasticity in the current collector (thickness of plastic layer hp) and lithiation induced deformation of the bilayer electrode (electrode in-plane strain ε0 and bending curvature κ) with respect to the SOC have been established. Key parameters that influence the elastoplastic deformation are identified. It is found that plastic yield of current collector reduces the restriction of current collector to active layer,and therefore,enhances the growth rate of in-plane stretching but lowers down the rate of electrode bending. In addition,the smaller thickness ratio of hc/h1 and higher modulus ratio of E0 ' /Ec ' would lead to earlier plastic yield of current collector as well as the larger in-plane strain and smaller bending curvature,due to the balance between current collector and active layer. The smaller yield stress and plastic modulus have the similar impacts on the electrode deformation. This paper systematically investigates the deformation of bilayer electrode. It is expected that the present work will have important potential in the in-situ electrochemical experiments based on bilayer electrodes.
| [1] | Tarascon, J. M. and Armand, M. Issues and challenges facing rechargeable lithium batteries. nature, 414(6861), 359–367 (2001) |
| [2] | Bourlot, S., Blanchard, P., and Robert, S. Investigation of aging mechanisms of high power Li-ion cells used for hybrid electric vehicles. Journal of Power Sources, 196, 6841–6846 (2011) |
| [3] | Zhang, J., Lu, B., Song, Y., and Ji, X. Diffusion induced stress in layered Li-ion battery electrode plates. Journal of Power Sources, 209, 220–227 (2012) |
| [4] | Song, Y., Shao, X., Guo, Z., and Zhang, J. Role of material properties and mechanical constraint on stress-assisted diffusion in plate electrodes of lithium ion batteries. Journal of Physics D: Applied Physics, 46(10), 105307 (2013) |
| [5] | Yang, B., He, Y. P., Irsa, J., Lundgren, C. A., Ratchford, J. B., and Zhao, Y. P. Effects of composition-dependent modulus, finite concentration and boundary constraint on Li-ion diffusion and stresses in a bilayer Cu-coated Si nano-anode. Journal of Power Sources, 204, 168–176 (2012) |
| [6] | Song, Y., Lu, B., Ji, X., and Zhang, J. Diffusion induced stresses in cylindrical lithium-ion batteries: analytical solutions and design insights. Journal of the Electrochemical Society, 159(12), A2060–A2068 (2012) |
| [7] | Sethuraman, V. A., Chon, M. J., Shimshak, M., Srinivasan, V., and Guduru, P. R. In situ measurements of stress evolution in silicon thin films during electrochemical lithiation and delithiation. Journal of Power Sources, 195, 5062–5066 (2010) |
| [8] | Bower, A. F., Guduru, P. R., and Sethuraman, V. A. A finite strain model of stress, diffusion, plastic flow, and electrochemical reactions in a lithium-ion half-cell. Journal of the Mechanics and Physics of Solids, 59(4), 804–828 (2011) |
| [9] | Cui, Z., Gao, F., and Qu, J. Interface-reaction controlled diffusion in binary solids with applications to lithiation of silicon in lithium-ion batteries. Journal of the Mechanics and Physics of Solids, 61(2), 293–310 (2013) |
| [10] | Liu, P., Sridhar, N., and Zhang, Y. W. Lithiation-induced tensile stress and surface cracking in silicon thin film anode for rechargeable lithium battery. Journal of Applied Physics, 112(9), 093507 (2012) |
| [11] | Liu, X. H., Zheng, H., Zhong, L., Huang, S., Karki, K., Zhang, L. Q., and Huang, J. Y. Anisotropic swelling and fracture of silicon nanowires during lithiation. Nano Letters, 11(8), 3312–3318 (2011) |
| [12] | Zhao, K., Wang, W. L., Gregoire, J., Pharr, M., Suo, Z., Vlassak, J. J., and Kaxiras, E. Lithiumassisted plastic deformation of silicon electrodes in lithium-ion batteries: a first-principles theoretical study. Nano Letters, 11(7), 2962–2967 (2011) |
| [13] | Zhao, K., Pharr, M., Vlassak, J. J., and Suo, Z. Inelastic hosts as electrodes for high-capacity lithium-ion batteries. Journal of Applied Physics, 109(1), 016110 (2011) |
| [14] | Brassart, L., Zhao, K., and Suo, Z. Cyclic plasticity and shakedown in high-capacity electrodes of lithium-ion batteries. International Journal of Solids and Structures, 50(7), 1120–1129 (2013) |
| [15] | Gao, Y. F., and Zhou, M. Coupled mechano-diffusional driving forces for fracture in electrode materials. Journal of Power Sources, 230, 176–193 (2013) |
| [16] | Song, Y., Li, Z., and Zhang, J. Reducing diffusion induced stress in planar electrodes by plastic shakedown and cyclic plasticity of current collector. Journal of Power Sources, 263, 22–28 (2014) |
| [17] | Qi, Y., Guo, H., Hector, L. G., and Timmons, A. Threefold increase in the Young's modulus of graphite negative electrode during lithium intercalation. Journal of the Electrochemical Society, 157(5), A558–A566 (2010) |
| [18] | Zhang, X., Shyy, W., and Sastry, A. M. Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles. Journal of the Electrochemical Society, 154(10), A910–A916 (2007) |
 2016, Vol. 37
2016, Vol. 37




















