Shanghai University
Article Information
- Denghui LI, Jianhua XIE. 2016.
- Symbolic dynamics of Belykh-type maps
- Appl. Math. Mech. -Engl. Ed., 37(5): 671-682
- http://dx.doi.org/10.1007/s10483-016-2080-9
Article History
- Received Jun. 6, 2015
- Revised Sept. 20, 2015
The symbolic dynamics plays an important role in the study of nonlinear dynamical systems. For the piecewise monotone interval maps,the kneading theory established by Milnor and Thurston[1] is an effective tool to describe their dynamical behavior. The kneading sequences, which are topological invariant,determine all admissible itineraries of the systems. There are various applications of the kneading theory in mechanical,physical,and chemical systems[2, 3, 4].
As an analogue to the kneading sequences in the one-dimensional case,Cvitanović[5] and Cvitanović et al.[6] introduced the concept of pruning front for a class of horseshoe type maps on the plane such as the Hénon[7] and Lozi maps[8]. They regarded the strange attractor of a map of this type as an incomplete horseshoe and conjectured that all its allowed symbol sequences can be completely determined by its pruning front and primary pruned region,there are no sequences pruned out by other mechanisms,and all other forbidden regions of the symbol space are obtained by backward and forward iterations of the primary pruned region.
Unlike the one-dimensional case,there is no single “maximal point” for two-dimensional maps,and each sheet defines a locally largest allowed itinerary. The pruning front can be computed by determining the primary homoclinic tangencies. (Primary tangencies are those tangencies which lie closest to the x-axis.) The connecting line of the pre-images of all primary tangencies gives a suitable partition of the phase space. Thus,for each point of the attractor or some invariant set,there is a corresponding two-sided symbol sequence. A key step is to give an order on the symbol plane in terms of the dynamics nature of the local stable and unstable manifolds. Using these facts,one can obtain the relation between the phase space and symbol space. However,for the Hénon map,the pruning front conjecture is proved only in certain parameter regions[9, 10],and most of the literatures focus mainly on the numerical investigation[11, 12, 13]. One of the main difficulties is that it is unable to formulate the positions of all homoclinic tangencies. Fortunately,for the Lozi map and the map considered in this paper, primary tangencies lie on the x-axis. The study is thus comparatively easier. Ishii[14, 15] proved the pruning front conjecture for the Lozi map and used that to study the dynamics of the map.
Non-smooth dynamical systems often come from the mechanical systems with the impact[16, 17, 18, 19, 20, 21],the dry friction[22, 23, 24, 25, 26],and so on. Non-smoothness is an important origin for the complexity of these systems. In the non-smooth case,even those piecewise linear systems can appear very complex dynamics behavior. The Belykh map (a two-dimensional discontinuous piecewise linear map) is a well-known example.
The Belykh map was introduced by Belykh[27] as a simple model in the phase synchronization theory. In this paper,we rewrite the Belykh map in a convenient form as


Under certain conditions,the map f has a strange attractor as shown in Fig. 1. Tél[28] calculated the Box dimension of the strange attractor of a similar map. The statistical properties of the attractors of a class of piecewise hyperbolic maps including the Belykh-type map,such as existence of Sinai-Ruelle-Bowen measures,exponential decay of correlations,and the central limit theorem were studied in Refs. [29]-[32].
 |
| Fig. 1 Strange attractor of map f for a = 1.5 and b = 0.3 |
The main aim of this paper is to prove the pruning front conjecture for the map f on an invariant set consisting of points with bounded orbits under a hyperbolicity condition. Furthermore,we construct a topological dynamics model and solve the boundary of horseshoes for f.
2 Hyperbolic cone fieldIn this section,we construct a hyperbolic cone field for the map f. We only construct the unstable cones. The construction of the stable ones is similar.
Suppose that a > b + 1. For all points that do not lie on the y-axis,let


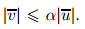 . Substituting
. Substituting 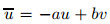 and
and 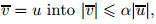 ,we obtain
The inequality (1) holds if
Since |v| ≤ α|u|,the inequality (2) holds if
,we obtain
The inequality (1) holds if
Since |v| ≤ α|u|,the inequality (2) holds if

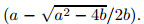 . Besides,we need to show that Df expands the
vectors in the unstable cone. Since |v| ≤ α|u| and
. Besides,we need to show that Df expands the
vectors in the unstable cone. Since |v| ≤ α|u| and 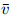 = u,we have |v| ≤ α|
= u,we have |v| ≤ α|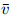 |. By |
|. By |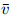 | ≤ α|
| ≤ α|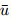 |,and
|,and
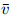 = u,we obtain |u| ≤ α|
= u,we obtain |u| ≤ α|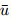 |.
|.
Similar calculations show that there exists the largest  such that if
|
such that if
|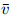 | ≥ β|
| ≥ β|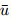 |,then |v| ≥ β|u|,|u| ≥ β|
|,then |v| ≥ β|u|,|u| ≥ β|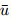 |,and |v| ≥ β|
|,and |v| ≥ β|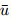 |. Note that α < 1 < β when a > b + 1.
|. Note that α < 1 < β when a > b + 1.
For the map f,its Jacobian matrix is independent of points. Thus,when a > b + 1,if a point whose orbit does not lie on the y-axis,then its stable and unstable subspaces are the eigenspaces of stable and unstable eigenvalues,respectively. This is the reason why in Theorem 2,the slopes of the stable and unstable leaves are constants.
3 Map from symbol plane to KIn this paper,we focus on the symbolic dynamics of the map f on an invariant set K
consisting of all points whose forward and backward orbits are bounded. Similar to the Lozi
map,we regard f : K → K as an incomplete horseshoe and its symbol model as a subshift on
two-sided symbol space  endowed with the usual metric. The key step is to determine
which sequence of the symbol space is disallowed. We use the ingredients developed by Ishii
in Ref. [14] for the Lozi map to construct the pruning front and primary pruned region of
f : K → K.
endowed with the usual metric. The key step is to determine
which sequence of the symbol space is disallowed. We use the ingredients developed by Ishii
in Ref. [14] for the Lozi map to construct the pruning front and primary pruned region of
f : K → K.
First,we show that the invariant K is contained in a square region.
Proposition 1 Suppose that a > b + 1,and let that R = 1/(a − b − 1). The invariant set K is contained in
Proof We define a partition of the plane by

First,it is easy to check that when a > b + 1,we have f(M1) ⊂ M3,f(M3) ⊂ M1,f −1(M2) ⊂ M4,and f −1(M4) ⊂ M2 (see Fig. 2).
 |
| Fig. 2 Partition of phase plane |
We denote the image of the point (x0,y0) by (x1,y1) and use negative subscripts for preimages.
We will show any point outside the region M0 whose orbit is unbounded. For any point (x0,y0) ∈ M1,we have

For any point (x0,y0) ∈ M2,we have

By the symmetry of the map f,we have |x1| > |x0| for any point (x0,y0) ∈ M3 and |y−1| > |y0| for any point (x0,y0) ∈ M4. This completes the proof of the proposition.
For a point X = (x,y) ∈ K,we put its itinerary as


We construct a map from the symbol space to the phase space which is the inverse of the projection map π on π(K). Note that the map f is equivalent to
Let us consider the Banach space f∞ of all bounded sequences endowed with the supremum
norm. For each sequence  of two-sided symbol space
of two-sided symbol space  ,we
define the operator
,we
define the operator

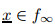 and
and 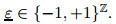
Theorem 1 Suppose that a > b + 1. Then,
(i) for any sequence  ,there exists a unique fixed point
,there exists a unique fixed point  of
of  ,for all
,for all  satisfies
satisfies
(ii)  satisfies (3),if and only if for all
satisfies (3),if and only if for all  ,
,
Proof Take any two different sequences  . We have
. We have

When a > b + 1,the operator  is contractive on the space f∞. Therefore,by the contraction
map principle,for each sequence
is contractive on the space f∞. Therefore,by the contraction
map principle,for each sequence  has a unique fixed point
has a unique fixed point  The statement
(ii) of Theorem 1 is obtained by comparing (3) and (4).
The statement
(ii) of Theorem 1 is obtained by comparing (3) and (4).
Write

which is the set of admissible symbol sequences for the map f : K → K.
Lemma 1 Let  . The map
. The map  is onto and gives the
inverse of the map π on π(K).
is onto and gives the
inverse of the map π on π(K).
Proof For each X ∈ K,let (xn,xn−1) = fn(X),then,the sequence {xn} ∈ f∞ satisfies
(3). Take any symbol sequence  ,by the definition of itinerary,we know εnxn ≥ 0.
Thus,{xn} satisfies (4) and is the fixed point of
,by the definition of itinerary,we know εnxn ≥ 0.
Thus,{xn} satisfies (4) and is the fixed point of  ,therefore,the map
,therefore,the map  is
onto. Besides,in the above proof,the choice of the itinerary of π(X),X ∈ K is arbitrary,and
the fixed point of the operator is unique,therefore,for each X ∈ K,we have
is
onto. Besides,in the above proof,the choice of the itinerary of π(X),X ∈ K is arbitrary,and
the fixed point of the operator is unique,therefore,for each X ∈ K,we have  .
.
For a symbol sequence · · · ε−2ε−1 · ε0ε1 · · · of  ,we call
,we call  = · · · ε−2ε−1 and
= · · · ε−2ε−1 and  =ε0ε1 · · · the tail and head of
=ε0ε1 · · · the tail and head of  ,respectively. We will show in this section that the map
,respectively. We will show in this section that the map  maps all sequences with a fixed tail (resp. head) into a line which we will denote by
maps all sequences with a fixed tail (resp. head) into a line which we will denote by  (resp.
(resp.
 ),and its intersection with the x-axis is the point
),and its intersection with the x-axis is the point  . Moreover,
. Moreover, (resp.
(resp.  ) is expressed by a power series in terms of a,b,and
) is expressed by a power series in terms of a,b,and  (resp.
(resp.  ). We will use the
series p(
). We will use the
series p( ) and q(
) and q( ) to construct the pruning front and primary pruned region for the map f
on K in the following section.
) to construct the pruning front and primary pruned region for the map f
on K in the following section.
Lemma 2 The map  is continuous on the symbol space
is continuous on the symbol space  .
.
Proof Take two sequences  such that εn = ε'n for all |n| ≤ N +1. For any
initial sequence
such that εn = ε'n for all |n| ≤ N +1. For any
initial sequence  ,we have
,we have  . As N becomes bigger,
. As N becomes bigger, and
and  will be arbitrarily close. Therefore,the map
will be arbitrarily close. Therefore,the map  is continuous.
is continuous.
Let Cu (resp. Cs) be the set of all tail (resp. head) of the elements in  and define
two breaches of f as
and define
two breaches of f as

Theorem 2 Suppose that a > b + 1.  maps symbol sequences with the same tail
maps symbol sequences with the same tail  (resp. head
(resp. head  ) into a line whose slope and intersection with the x-axis are expressed by power
series expansions using a,b,and the tail (resp. head) only.
) into a line whose slope and intersection with the x-axis are expressed by power
series expansions using a,b,and the tail (resp. head) only.
Proof We see that the following diagram commutes:

The diameter of the cylinder set · · · ε−3ε−2ε−1 · Cs converges to zero under σ−n (n > 0). By
the uniform continuity of  ,the diameter of set
,the diameter of set  converges to zero
by the following iterations:
converges to zero
by the following iterations:

Since there exists a hyperbolic cone field for the map f (see Section 2),we see that the tangent
vectors of  are contained in
are contained in

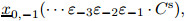 ,and TY denotes the tangent space at the point
Y . Consequently,the set
,and TY denotes the tangent space at the point
Y . Consequently,the set 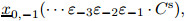 is contained in a line.
is contained in a line.
Next,let us determine the slope of the line and its intersection with the x-axis. Take two
sequences with the same tail  Let
Let
 and
and  be the fixed points of
be the fixed points of  and
and  ,respectively. From (4),the
slope of the line containing
,respectively. From (4),the
slope of the line containing  and
and  is
is

We consider the following continued fraction:

We have
when a > b + 1,since the map

is contractive on the interval

if a2 > 4b and the ratio (x−n −x' −n)/(x−n+1 −x' −n+1) is in this interval as we saw above. Thus,
we have proved that  maps every ε with a fixed tail · · · ε−2ε−1· on a line
maps every ε with a fixed tail · · · ε−2ε−1· on a line  for some p.
for some p.
Finally,we determine the value of p. As above,we have (xn − x' n)/(xn+1 − x' n+1) = s for
all  ,and the point (xn,xn−1) lies on a line of the form: y = s(x − pn−1) for some pn−1.
Substituting xn−1 = s(xn − pn−1) and xn = s(xn+1 − pn) into (4),we obtain the recursion
pn = εn − bspn−1. Thus,
,and the point (xn,xn−1) lies on a line of the form: y = s(x − pn−1) for some pn−1.
Substituting xn−1 = s(xn − pn−1) and xn = s(xn+1 − pn) into (4),we obtain the recursion
pn = εn − bspn−1. Thus,
Similarly,we see that  maps sequences with a fixed head Cu · ε0ε1ε2 · · · into a line
maps sequences with a fixed head Cu · ε0ε1ε2 · · · into a line  :
ry = x − q,where
:
ry = x − q,where
Remark 1 When a > b + 1,the series s,r,p,and q uniformly converge,and they are the continuous functions of ε,a,and b.
Remark 2 If an orbit of a point X ∈ K does not lie on the y-axis (in this case,the
itinerary π(X) is just one sequence  ),then the line
),then the line  contains the local stable
manifold Wlocs(x) and local unstable mainfold Wloc u (x) of the point X (see Fig. 3). We remark
that these lines can also be defined for symbol sequences which are not itineraries of points in
the invariant K.
contains the local stable
manifold Wlocs(x) and local unstable mainfold Wloc u (x) of the point X (see Fig. 3). We remark
that these lines can also be defined for symbol sequences which are not itineraries of points in
the invariant K.
 |
Fig. 3 Lines  and and  |
Definition 1 For a symbol sequence  ,we call set
,we call set 
 an unstable (resp. stable) leaf.
an unstable (resp. stable) leaf.
In this section,we first give the definition of the pruning front and the primary pruned region of f on K and interpret their meanings. Then,we prove the pruning front conjecture.
Definition 2 We call


For a  , and
, and  . It is clear that the
intersection of
. It is clear that the
intersection of  and
and  is
is  . By Theorem 2,we know that the slope of
. By Theorem 2,we know that the slope of  is negative,
and that of
is negative,
and that of  is positive. Thus,ε−1(p− q) ≥ 0 if and only if
is positive. Thus,ε−1(p− q) ≥ 0 if and only if  . This gives another
characterization of the pruning front and the primary pruned region of f : K → K,i.e.,
. This gives another
characterization of the pruning front and the primary pruned region of f : K → K,i.e.,

Lemma 3 For each  ,we have
,we have  ,where σ is the shift operator.
,where σ is the shift operator.
Proof It is clear that

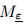 under the iteration of it.
under the iteration of it.
Now,we begin to prove the pruning front conjecture for f : K → K.
Theorem 3 Suppose that a > b + 1. Then,for a sequence  ,there exists a
point X ∈ K such that
,there exists a
point X ∈ K such that  if and only if
if and only if  does not lie in Df for all n ∈
does not lie in Df for all n ∈  .
.
Proof By Theorem 1,we know that a symbol sequence  is admissible if and only if
is admissible if and only if
 for all
for all  . Using the other characterization of the pruning front and the
primary pruned region of f : K → K above and Lemma 3,we obtain
. Using the other characterization of the pruning front and the
primary pruned region of f : K → K above and Lemma 3,we obtain

Thus,all allowed symbol sequences of f : K → K are completely determined by Pf and Df.
6 Partial order in symbol planeNow,we explain the relation between the above definition of the pruning front and the
primary pruned regions of f : K → K and the original idea of Cvitanović et al.[6]. Represent
 as the direct sum of Cu and Cs,i.e.,
as the direct sum of Cu and Cs,i.e., . Recall that Cu (resp. Cs)
is the set of all tails (resp. heads). First,we define a partial order in the symbol plane (see
Fig. 4).
. Recall that Cu (resp. Cs)
is the set of all tails (resp. heads). First,we define a partial order in the symbol plane (see
Fig. 4).
 |
| Fig. 4 Symbol plane (+ and − stand for +1 and −1, respectively) |
Definition 3
(i) Take two distinct tails  and
and  in Cu. We can find the biggest integer i < 0 such that
in Cu. We can find the biggest integer i < 0 such that

(ii) Take two distinct heads  and
and  in Cs. We can find the smallest integer i ≥ 0 such that
in Cs. We can find the smallest integer i ≥ 0 such that

The following proposition shows that the map π preserves the order defined above.
Proposition 2 Suppose that a > b+1. Then,the map π is order preserving in the following
sense: take two points X and Y on an unstable (resp. stable) leaf,and suppose that Xx < Yx
(resp. Xy < Yy). Thus,for any  ,we have
,we have  .
.
Proof It suffices to show that if we take two points X and Y in an unstable leaf (resp.
stable leaf) and suppose Xx < Yx (resp. Xy < Yy),then we have f(X)x > f(Y )x (resp.
f(X)y < f(Y )y). This is true that,by Remark 2,for each point in the set K,its stable leaf (resp.
unstable leaf) expresses the contracting (resp. expanding) direction at it,and the eigenvalues
of the Jacobian matrix of f are  and
and  .
.
Remark 3 Under the partial order of the symbol plane defined above,the series p and q are the monotonically increasing function of tails and heads,respectively.
For a sequence  ,if
,if  ,then the stable and unstable leaves determined by
,then the stable and unstable leaves determined by
 are “tangent” on the x-axis (here,the “tangency” means that one endpoint of the unstable
leaf contacts with the stable leaf,as shown in Fig. 5). There exist two case: ε−1 = +1 or
ε
−1 = −1. We only discuss the first case. The discussion of the second case is similar. The
partial order of the symbol plane tells us that p (resp. q) is a monotonically increasing function
of
are “tangent” on the x-axis (here,the “tangency” means that one endpoint of the unstable
leaf contacts with the stable leaf,as shown in Fig. 5). There exist two case: ε−1 = +1 or
ε
−1 = −1. We only discuss the first case. The discussion of the second case is similar. The
partial order of the symbol plane tells us that p (resp. q) is a monotonically increasing function
of  (resp.
(resp.  ). By this and Remark 1,for any sequence
). By this and Remark 1,for any sequence  which satisfies
which satisfies  or
or
 ,and
,and  ,the operator
,the operator  cannot determine a point
cannot determine a point  in K. Thus,any sequence
in K. Thus,any sequence
 satisfying
satisfying  is disallowed (see Fig. 6).
is disallowed (see Fig. 6).
 |
| Fig. 5 Primary homoclinic tangency |
 |
| Fig. 6 Primary pruned region of map f : K → K |
 |
| Fig. 7 Boundary of horseshoes |
In this section,we construct a symbolic dynamics model for f : K → K. First,we define an equivalence relation in the set Af.
Definition 4 For two symbol sequences  ,we say that ε is equivalent to δ
if
,we say that ε is equivalent to δ
if  .
.
Let  be the quotient space of Af with respect to the above equivalence relation. For
any
be the quotient space of Af with respect to the above equivalence relation. For
any  ,we put
,we put  and
and  ,where [ε] denotes the
equivalent class of ε.
,where [ε] denotes the
equivalent class of ε.
The following theorem says that there is a symbol model for the dynamics of the map f on
K described by (Pf ,Df) only,and the model is a subshift on the quotient space  of Af.
of Af.
Theorem 4  is a homeomorphism from
is a homeomorphism from  to K such that the following commutative diagram holds:
to K such that the following commutative diagram holds:

Proof First,we note that the symbol space  is compact and that
is compact and that  is
open by the definition of the primary region Df. Therefore,
is
open by the definition of the primary region Df. Therefore, is a compact metric space,this also holds for its quotient space
is a compact metric space,this also holds for its quotient space  by the standard theory of
topology. Lemmas 1 and 2 show that
by the standard theory of
topology. Lemmas 1 and 2 show that  is a continuous surjection,and this also holds for
is a continuous surjection,and this also holds for
 . Moreover,
. Moreover, is one-to-one. Therefore,
is one-to-one. Therefore, is a continuous bijection from
the compact metric space
is a continuous bijection from
the compact metric space  to the Hausdorff space K,therefore,it is a homeomorphism.
The commutative diagram follows from Lemma 3.
to the Hausdorff space K,therefore,it is a homeomorphism.
The commutative diagram follows from Lemma 3.
In this section,we solve the boundary of the parameter region where the map f : K → K
has a horseshoe. Suppose that a > b + 1. Let
H := {(a,b) : f : K → K is equivalent to the shift map of the two-sided symbol space}.
Since the system is symmetrical,we only need to consider the case ε−1 > 0. Recall that  and
and  are monotonically increasing functions of
are monotonically increasing functions of  and
and  ,respectively. The smallest value
of p is
,respectively. The smallest value
of p is  which is associated to the tail · · · − − − +·. The biggest value of q is
which is associated to the tail · · · − − − +·. The biggest value of q is  which is associated to the head · + − + − · · ·. Parameter values (a,b) lie on the boundary of
the region H (see Fig. 3) if and only if
which is associated to the head · + − + − · · ·. Parameter values (a,b) lie on the boundary of
the region H (see Fig. 3) if and only if
Substitute (6) and (9) into (10). By a simple calculation,we obtain

| [1] | Milnor, J. and Thurston, W. On iterated maps of the interval. Dynamical Systems, Lecture Notes in Mathematics (ed. Alexander, J. C.), Springer, New York, 465–563 (1988) |
| [2] | Barrio, R., Shilnikov, A., and Shilnikov, L. Kneadings, symbolic dynamics and painting Lorenz chaos. International Journal of Bifurcation and Chaos, 22, 1230016 (2012) |
| [3] | Caneco, A., Grácio, C., and Rocha, J. Kneading theory analysis of the Duffing equation. Chaos Solitons Fractals, 42, 1529–1538 (2009) |
| [4] | Guckenheimer, J. and Scheper, C. A geometric model for mixed-mode oscillations in a chemical system. SIAM Journal on Applied Dynamical Systems, 10, 92–128 (2011) |
| [5] | Cvitanović, P. Periodic orbits as the skeleton of classical and quantum chaos. Physica D, 51, 138–151 (1991) |
| [6] | Cvitanović, P., Gunaratne, G., and Procaccia, I. Topological and metric properties of Hénon-type strange attractors. Physical Review A, 38, 1503–1520 (1988) |
| [7] | Hénon, M. A two-dimensional mapping with a strange attractor. Communications in Mathematical Physics, 50, 69–77 (1976) |
| [8] | Lozi, R. Un attracteur étrange du type attracteur de Hénon. Journal de Physique, 39, 9–10 (1978) |
| [9] | Mendoza, V. Proof of the pruning front conjecture for certain Hénon parameters. Nonlinearity, 26, 679–690 (2013) |
| [10] | Mendoza, V. A note about pruning and Hénon Maps. Qualitative Theory of Dynamical Systems, 12, 443–448 (2013) |
| [11] | Hagiwara, R. and Shudo, A. An algorithm to prune the area-preserving Hénon map. Journal of Physics A: Mathematical and General, 37, 10521–10543 (2004) |
| [12] | Hagiwara, R. and Shudo, A. Grammatical complexity for two-dimensional maps. Journal of Physics A: Mathematical and General, 37, 10545–10559 (2004) |
| [13] | Jaeger, L. and Kantz, H. Structure of generating partitions for two-dimensional maps. Journal of Physics A: Mathematical and General, 30, 567–576 (1997) |
| [14] | Ishii, Y. Towards a kneading theory for Lozi mappings I: a solution of the pruning front conjecture and the first tangency problem. Nonlinearity, 10, 731–747 (1997) |
| [15] | Ishii, Y. Towards a kneading theory for Lozi mappings II: monotonicity of the topological entropy and Hausdorff dimension of attractors. Communications in Mathematical Physics, 190, 375–394 (1997) |
| [16] | Whiston, G. S. Global dynamics of a vibro-impacting linear oscillator. Journal of Sound and Vibration, 118, 395–429 (1987) |
| [17] | Whiston, G. S. Singularities in vibro-impact dynamics. Journal of Sound and Vibration, 152, 427–460 (1992) |
| [18] | Nordmark, A. B. Non-periodic motion caused by grazing incidence in an impact oscillator. Journal of Sound and Vibration, 145, 279–297 (1991) |
| [19] | Molenaar, J., de Weger, J., and van de Water, W. Mappings of grazing impact oscillators. Nonlinearity, 14, 301–321 (2001) |
| [20] | Di Bernardo, M., Budd, C. J., Champneys, A. R., and Kowalczyk, P. Piecewise-Smooth Dynamical Systems: Theory and Applications, Springer-Verlag, London (2008) |
| [21] | Yue, Y. and Xie, J. H. Symmetry, cusp bifurcation and chaos of an impact oscillator between two rigid sides. Applied Mathematics and Mechanics (English Edition), 28, 1109–1127 (2007) DOI 10.1007/s10483-007-0813-z |
| [22] | Leine, R. I. and Nijmeijer, H. Dynamics and Bifurcations of Non-Smooth Mechanical Systems. Springer-Verlag, Berlin (2004) |
| [23] | Di Bernardo, M., Kowalczyk, P., and Nordmark, A. B. Sliding bifurcations: a novel mechanism for the sudden onset of chaos in dry-friction oscillators. International Journal of Bifurcation and Chaos, 13, 2935–2948 (2003) |
| [24] | Kowalczyka, P. and Piiroinenb, P. T. Two-parameter sliding bifurcations of periodic solutions in a dry-friction oscillator. Physica D, 237, 1053–1073 (2008) |
| [25] | Guardia, T. M., Seara, T., and Hogan, S. J. An analytical approach to codimension-2 sliding bifurcations in the dry friction oscillator. SIAM Journal on Applied Dynamical Systems, 9, 769– 798 (2010) |
| [26] | Guo, Y. and Xie, J. H. Neimark-Sacker (N-S) bifurcation of oscillator with dry friction in 1:4 strong resonance. Applied Mathematics and Mechanics (English Edition), 34, 27–36 (2013) DOI 10.1007/s10483-013-1650-9 |
| [27] | Belykh, V. Qualitative Methods of the Theory of Nonlinear Oscilaltions in Point Systems, Gorki University Press, Gorki (1980) |
| [28] | Tél, T. Fractal dimension of the strange attractor in a piecewise linear two-dimensional map. Physics Letters A, 97, 219–223 (1983) |
| [29] | Young, L. S. Bowen-Ruelle measures for certain piecewise hyperbolic maps. Transactions of the American Mathematical Society, 287, 41–48 (1985) |
| [30] | Pesin, Y. B. Dynamical systems with generalized hyperbolic attractors: hyperbolic, ergodic and topological properties. Ergodic Theory and Dynamical Systems, 12, 123–151 (1992) |
| [31] | Afraimovich, V., Chernov, N., and Sataev, E. Statistical properties of 2-D generalized hyperbolic attractors. Chaos, 5, 238–252 (1995) |
| [32] | Young, L. S. Statistical properties of dynamical systems with some hyperbolicity. Annals of Mathematics, 147, 585–650 (1998) |
 2016, Vol. 37
2016, Vol. 37












