Shanghai University
Article Information
- Xiaojing CAI, Jinquan XU.
- Interface models for thin interfacial layers
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 707-724
- http://dx.doi.org/10.1007/s10483-016-2084-6
Article History
- Received Sept. 21, 2015;
- Revised Nov. 24, 2015
Due to the wide applications of bonded dissimilar materials in engineering,the efficient and accurate interfacial stress analysis becomes more and more important. Physically,an interface is generally not a theoretical plane. It is an interfacial layer with very thin thickness and very complicate compositions. To deal with such thin interfacial layers in mechanical analyses,an interface model is necessary. The role of the interface model is to describe the effect of the complicate interfacial layer correctly in a simple effective way. However,there is not one universial effective interface model due to the complex bonding types[1, 2, 3]. What an interface model should be adopted for a specified joint or how to ensure the reliability of the analyzed results is not clear yet. The motivation of this study is to develop a simple but efficient and accurate interface model,by which no pre-assumption or experience on the parameter selection is necessary.
2 Typical interface models 2.1 Classic modelThe classic interface model[4, 5] regards the interfacial layer as a theoretical plane,and assumes that the displacements and tractions at the plane are continuous. That is, the mechanical condition at the interface is assumed as follows:
where p and u denote the traction vector and the displacement vector,respectively. The suffixes 1 and 2 denote the two sides of the interface. In this model,the effect of the physical interfacial layer is neglected. This model was originally developed from the continuous condition at an imaged plane in a continuous body,and has successfully been extended to the cases with very thin interfacial layers and the cases with a relatively clear bonding interface such as coatings and adhesives. As it will be illustrated later,this model can also give accurate results for a bonding with hard interfacial layers though it is neglected in fact in the analysis. No empirical parameter is needed to be pre-assumed for the layer. However,this model cannot be used to deal with the joints with soft interfacial layers. Hard and soft layers are very important concepts in traditional interface models. Usually,different models should be adopted for hard and soft layers. However,they are basically only relative concepts mainly based on the view of Young's modulus of the physical interfacial layer. Therefore,it is quite difficult to determine whether the layer is hard or soft in engineering applications.
2.2 Direct modelApproximate the complicate interfacial layer as a homogeneous material. Then,the interfacial layer in the direct model can be regarded as an inserted material at the bonding places,and the interfaces between the inserted material and the joint materials can be assumed as the classic interfaces,which are imaged planes rather than a physical existence. That is,two interfaces with the mechanical condition shown in Eq. (1) are used to express the effect of the interfacial layer. This model seems strict if the material properties of the inserted material has been assumed correctly. However,it contains a fatal shortage in the numerical procedures due to the thin middle layer,which will usually induce great difficulties in the accuracy and efficiency and even make the analysis impossible. By the way,if the interfacial layer is relatively thick,it is true that,there may be a stable region corresponding to a homogeneous material,where the properties of the inserted material may be still different from that of the stable region since it may also contain the effect of non-stable regions in the interfacial layer. It must be pointed out that the inserted material in this model is a mechanical equivalent or effective material rather than an actual material.
2.3 Cohesive modelCohesive models[6, 7, 8] have been widely used in the interfacial fracture simulation. A cohesive model regards the interfacial layer as spring (linear or nonlinear),and the spring constants must be pre-assumed empirically. That is,the mechanical condition at the interface is assumed as follows:
where Fn and Ft are the normal force and the tangential force acted on the interface,respectively,and Δun and Δut are the normal displacement jump and the tangential displacement jump,respectively. The functions f1 and f2 can be linear or nonlinear,but must be pre-assumed. Such a model has been successfully used in the bonding with soft interfacial layers[9, 10, 11, 12]. With this model,various simulation analyses become possible just by pre-assuming the proper spring behaviors. However,whether it is believable or not must be proved by the experimental or stress results obtained by other methods. A physical interfacial layer is a continuum,despite of being thin. From the view of mechanics, replacing a continuum by springs may lead to some contradictions. For examples,stresses are usually assumed to depend only on the corresponding displacement jumps in the spring models,i.e.,normal stresses depend only on the normal jump and shear stresses depend only on the tangential jump. However,the constitutive continuum obviously implies interactions. An interfacial stress is assumed to be determined by the displacement jumps at the point only,and the displacements at the neighbor points have no effect on it. However,the continuum mechanics indicates that it must be determined by the displacement distribution rather than the displacement at the point. Though other stress components within the interfacial layer (e.g.,components parallel to the interface) have been neglected absolutely,it may be quite large and will play an important role on the interfacial failure[13]. These contradictions mean that the mechanical fundamental equations are not satisfied completely if a spring model is adopted. Thereby,a cohesive model can be applied only for the case where these contradictions can be neglected. But when can they be neglected? Clarifying the condition of the applying cohesive model is meaningful,though currently it is generally not concerned.
3 Constitutive-based modelFrom the above investigations on the current interface model,it can be seen that developing a complete interface model is meaningful to avoid the pre-assumption or experience for the analysis. For simplicity,a plane problem is considered here. Set the interface layer along the y-axis and its normal direction along the x-axis. Then,the physical model bonding with an interfacial layer can be shown as Fig. 1(a),where the two classic interfaces satisfy the continuous condition in Eq. (1) before the interfacial layer is replaced by an interface model. Model the interfacial layer as an interface with zero thickness (called as the modelled interface below). Then,the bonding geometry can be simplified as Fig. 1(b). However,one must be always aware of that the modelled interface in Fig. 1(b) is able to represent the physical interfacial layer. Therefore,the relationship between the traction and the displacement at the modelled interface cannot be assumed, but must be deduced from the constitution of the interfacial layer. It is true that the composition of the interfacial layer is very complicate and the constitution may also be very complicate. However,it is possible to represent the complicate interfacial layer by an equivalent homogeneous layer with effective mechanical properties,just as that in a direct interface model. Here,we consider the relationships at the modelled interface by taking the interfacial layer into account.

|
| Fig. 1 Modelling process of interface |
Let A and B be the corresponding pair of points at the two sides of the physical interfacial layer,which will be overlapped into a same point at the modelled interface. However,the displacement and traction at A and B,i.e.,uA,vA,σxA,and τxyA and uB,vB,σxB,and τxyB, must be different. Therefore,the modelled interface is a discontinuous plane mathematically with discontinuous displacement and traction. Thereby,there are eight interfacial variables at a point on the modelled interface in total. The stress component parallel to the interface within the interfacial layer (σY) disappears at the modelled interface,but it should be able to be revivified or computed from the traction and displacement at the modelled interface. According to the knowledge of the continuum mechanics,only four unknowns at the interface can be solved for plane problems. This fact means that four additional relationships between uA,vA,σxA,and τxyA and uB, vB,σxB,and τxyB must be introduced for the analysis. Denote
where u and v are the displacements at the interface, and Δu and Δv are the displacement jumps across the modelled interface. To obtain the unknowns u,v,Δu,and Δv,the following four relationships are prepared:It can be easily found that the above relationships relate the stresses and the displacement jumps together. Therefore,they should be deduced theoretically rather than pre-assumed. In the classic interface model,the following relations are pre-assumed:
while in a cohesive model,the pre-assumptions arewhere the functions f1 and f2 can be linear or nonlinear. Obviously,both theses two pre-assumptions may be different from the true role of the interfacial layer,though they may be an accurate enough approximation of Eq. (4) indeed under some special situations.
The material properties of the interfacial layer in fact are very complicate. It may be even different from point to point,since its composition varies dramatically within its thickness. However,the stress analysis with a complicate constitute reflecting actually the composition's variation is neither necessary nor possible. An equivalent continuous body with a relatively simple constitution is a practice alternative to simulate its mechanical behavior. For the simplicity,assume that the interfacial layer is linearly elastic (in other words,consider the interfacial layer as an equivalent linear elastic material). Then,the constitutive model can be expressed as follows:
where μ =E/(2(1+ν)) is the shear modulus of the interfacial layer in which E is Young's modulus and ν is Poisson's ratio,and κ is the elastic constant defined by If the thickness of the interfacial layer is very small,referring to Fig. 1(a),we have where δ is the thickness of the interfacial layer. It is noted that Eq. (8) is basically an approximation rather than a pre-assumption. The thinner the thickness is,the higher the accuracy becomes.Applying Eq. (6) to points A and B,we have
The above relationships are obviously different from the linear cohesive model shown below:The traction deduced from the constitution depends on not only the corresponding displacement jumps but also the neighbor displacement variation. Only for the case that the partial differentials of the displacement along the interface can be neglected,Eq. (9) can be degraded to a cohesive model. In other words,a cohesive model can be used only for the cases that the distribution effect of the displacement along the interface can be neglected. Some important remarks can be concluded from the degradation of Eqs. (9) and (10):
(ⅰ) The spring constants in a cohesive model for the normal and shear stresses are neither independent nor the same. The relationship between the normal stiffness and the shear stiffness is

(ⅱ) The spring constants depend on the thickness of the physical interfacial layer. These two remarks may be very useful in the pre-assuming spring constants of the cohesive model. Compared with the cohesive model,Eq. (9) is a generalized relationship at the modelled interface,without any pre-assumption but with an approximation of the interfacial layer by an effective homogeneous layer.
The stress component parallel to the interface within the interfacial layer can be expressed by
whereIt should be pointed out that Eq. (11) implies the assumption that σy is uniform along the thickness direction. If its distribution along the thin thickness is also needed,zooming up techniques can be used,since both the tractions and the displacements at the two sides of the interfacial layer can be obtained before calculating σy(x). Anyway,Eq. (11) means that the stress components parallel to the interface can also be analyzed if Eq. (9) is used as the interface model,even the thickness has been modelled as zero.
Rewrite Eq. (9) as follows:
where k1,k2,k12,and k21 are the material constants of the interfacial layer defined by Then,we can obtain the relationships on the modelled interface, which are appropriate for the numerical analysis. It is noted that the partial derivatives of the displacements appeared in Eq. (13) can be expressed by the displacements and their jumps through the numerical technology. Equation (13) provides four relationships on the modelled interface. Therefore,it is sufficient to make the numerical analysis possible,and it will be called as the constitutive-based model below.By the way,replace the x-axis by the normal direction and the y-axis by the tangential direction. Then,a curved interfacial layer can be dealt with just by taking proper coordinate transformations.
4 Numerical procedureSince u,Δu,v,and Δv have been set as unknowns,the numerical procedure must be adjusted to match these unknowns. Here,we show the boundary element method (BEM) formulization for the constitutive-based interface model. Adopting an iso-parametric element (see Fig. 2),we have[14]
where and ξ is the normalized local coordinate.

|
| Fig. 2 Boundary elements used for interface model |
Since
the partial derivatives of the displacements and jumps appeared in Eq. (13) are those defined at the interface only. Since the interface has been set along the y-axis here,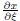 =0. For a curved interface,this is also true
when the x-axis is regarded as the normal direction. Therefore,
we have
where
Adopt the matrix expressions. Then,the tractions at the two sides
of the modelled interface shown in Eq. (13) can be expressed as
follows:
where
The boundary integral equation can also be expressed in a matrix
expression as follows[14]:
where p* and u* are the
fundamental solutions. Applying Eq. (22) on a boundary node in
Material "1" or "2" as shown in Fig. 1(b),we have
where
=0. For a curved interface,this is also true
when the x-axis is regarded as the normal direction. Therefore,
we have
where
Adopt the matrix expressions. Then,the tractions at the two sides
of the modelled interface shown in Eq. (13) can be expressed as
follows:
where
The boundary integral equation can also be expressed in a matrix
expression as follows[14]:
where p* and u* are the
fundamental solutions. Applying Eq. (22) on a boundary node in
Material "1" or "2" as shown in Fig. 1(b),we have
where
In Eq. (23),the upper suffix denotes Material "1" or "2". The number of the boundary element of the region k (k=1,2) is denoted by NEk,and the number of the element at the modelled interface is denoted by NI. For all nodes in Material 1,Eq. (23a) can be rearranged as follows:
and for all nodes in Material 2,Eq. (23b) can be rearranged as follows: where Uj(j=1, 2) are the total vectors of the displacements for the nodes belonging to Material j only, U Iand ΔU are the total vectors of the displacements and their jumps at the interface nodes,and pj(j=1, 2) denote the total vectors of the surface tractions for the nodes belonging to Material j only.Arranging Eq. (25) into a total matrix form,we have
Move the unknowns to one side. Then,we have After solving Eq. (27),the tractions at the modelled interface (for both the left- and right-sides) can be calculated by Eq. (13). Denote the neighbored node numbers as ν (noting that several nodes near the interface edge must be excluded due to the edge singularity[15, 16]). Then,we have The stress component parallel to the interface within the interfacial layer can be evaluated from Eq. (11) as follows: According to Eq. (28),all stress components of the interfacial layer can be determined absolutely,though the thickness of the interfacial layer has been modelled as zero in the analysis. 5 Numerical examinations and comparisonsThe above formulization has been coded into BEM2D (see Ref. [16] for the details). The physical bonding model is shown in Fig. 3(a) with the size of k21,and the mesh divisions are shown in Figs. 3(b) and 3(c). Here,for the sake of the numerical analysis of the direct model,it is assumed that the thickness of the interfacial layer is relatively large. For the purpose of comparison and verification,four kinds of analyses with different interface models,i.e.,the direct model (denoted by strict),the classic model (denoted by classic),the cohesive model (denoted by cohesive),and the constitutive-based model (denoted by constitutive-based),are carried out. Two kinds of interfacial layers,i.e., hard layer and soft layer,are considered. In the cohesive model,



|
| Fig. 3 BEM analysis model and element divisions |
The spring constants of the cohesive model in Table 1 are determined by fitting the stress results to that obtained by other interface models. It can be seen that,for a soft interfacial layer,they are just the same as those of the constitutive-based model,but for a hard layer,k1co is obviously different from k1, while k2co is always the same as k2.
Figure 4 shows the examples of the deformation under the remote
tensile loading and the remote shear loading for a joint with a
hard interfacial layer. Limit to the deformations,no obvious
difference is observed for different interface models. The right
graphs of Fig. 4 show that the deformations of the interfacial
layer are uniform approximately under both the remote tensile
loading and the remote shear loading. This fact means that the
partial derivative  is so small
that a cohesive model can be adopted.
is so small
that a cohesive model can be adopted.

|
| Fig. 4 Deformations under different loadings with hard interfacial layer |
Figure 5 shows the interfacial stresses obtained by different models for a hard interfacial layer. It can be found that the results agree well with each other. This fact means that the new constitutive-based interface model is correctly coded. It can also be found that the difference of tractions (i.e.,the jumps) between the two sides of the interfacial layer is very small. It should be noted that the results of the cohesive model depend on the setting of the spring constants,which are determined here by other analyzed results which will be given later. Therefore,the agreement of the results obtained by the cohesive model to others is not always true if the spring constants are different from those shown above.

|
| Fig. 5 Comparison of interfacial stresses with different interface models for hard interfacial layer |
Figure 6 shows the interfacial stresses for a soft interfacial layer. Unlike the case of a hard interfacial layer,the classic interface model is no longer appropriate. It can be found that the results obtained by other models agree well with each other.

|
| Fig. 6 Comparison of interfacial stresses with different interface models for soft interfacial layer |
From Figs. 5 and 6,it can be concluded that there is no obvious difference among the results obtained by the direct model,the cohesive model,and the constitutive-based model. But this conclusion must be limited to the traction at the modelled interface only. The stress within the interfacial layer (σy) cannot be analyzed by a cohesive model.
Figure 7 shows the distribution of the stress parallel to the interface. The strict result refers to the internal points at x=0.05 mm,while the result of the constitutive-based model is calculated from Eq. (28c) after the displacements and their jumps at the modelled interface have been obtained. It can be seen that they agree with each other very well. This examination shows that all stress components within the interfacial layer are possible to be analyzed by the constitutive-based model. It is noted that the results obtained by the direct model may become inaccurate if the thickness of the interfacial layer is very thin (for the sake of comparison,it has been set relatively thick in this examination), while the constitutive-based model does not have such a limitation.

|
| Fig. 7 Stresses parallel to interface within interfacial layers |
Figure 8 shows the relationship between the tractions (the average of two sides of the modelled interface) and the displacement jumps obtained by the direct model and the constitutive-based model for the hard interfacial layer,and Fig. 9 shows the relationship between the tractions (the average of two sides of the modelled interface) and the displacement jumps obtained by the direct model and the constitutive-based model for the soft interfacial layer. It can be found that the results are linear. The slopes of the relationship are obviously just the spring constants of the cohesive model. It is noted that,for a hard interfacial layer,the slope of the normal stress is quite different from that shown in Table 1. This fact means that,to the pre-assume spring constants,the stress-displacement's jump relationship must be analyzed by other methods at first,otherwise,arbitrarily assumed spring constants are only imaged values and thereby cannot represent the true role of the interfacial layer. For the soft layer,it can be seen that the spring constants in a cohesive model can be estimated by k1 and k2 directly. In practical applications, however,one may encounter the difficulty of judging soft or hard if a cohesive model is adopted. It is really not easy and may even be case by case. While by the constitutive-based model,no attention is needed to be paid whether it is soft or hard . More importantly,no matter the variation of the displacement along the interface can be neglected or not (which is the condition of the used cohesive model),the constitutive-based model is always valid.

|
| Fig. 8 Numerical relationships between traction and displacement jumps for hard interfacial layer |

|
| Fig. 9 Numerical relationships between traction and displacement jumps for soft interfacial layer |
Introduce an edge interface crack with the length a=10 mm in the analysis model shown in Fig. 1. Keep other analysis conditions the same as those described above. Then,the traction and displacement jumps can be analyzed by the constitutive-based model. The numerical relationships between them are shown in Fig. 10. It can be found that the slope of the normal stress relationship for the hard layer becomes 2 200 GPa·mm-1,different from that (1 528 GPa·mm-1) for the non-cracked interface. This fact means that the spring constant in a cohesive model for the hard interfacial layer may be geometry-dependent. For a soft interfacial layer,however,no such a dependency can be observed. This is the reason why the cohesive model is more appropriate for a soft interfacial layer rather than a hard interfacial layer.

|
| Fig. 10 Relationships between traction and displacement jumps at interfacial crack front |
For a nonlinear interfacial layer,assume that its constitution can be expressed in a power-law way as follows:
where β and m are the material constants,and σ and ε denote the equivalent stress and strain,respectively. Then,we have[17] where the equivalent stress can be expressed as follows: Substituting Eq. (30) into Eq. (31) yields for both the plane strain state and the plane stress state.Applying Eqs. (30) and (32) on Interfaces 1 and 2 shown in Fig. 1(a) and using the definition of the displacement jump of Eq. (3),we can get the mechanical condition at the modelled interface as follows:
The above relationships are deduced theoretically from the nonlinear constitutive model of the interfacial layer. Therefore, no pre-assumption has been introduced. Neglecting the effects of the displacement variation along the interface,a nonlinear cohesive model can be obtained,i.e., where It can be seen that the nonlinear cohesive model must consider the effect of the displacement jump at other directions (the interaction effect),and the nonlinear spring constant for the normal stress is always two times larger than that for the shear stress. 7 Three-dimensional constitutive-based modelSet the interfacial layer along the xy-plane and its thickness direction along the z-axis. Denote the corresponding pair of points at the two sides of the physical interfacial layer as A and B (see Fig. 11(a)). Then,there will be 12 interfacial variables in total at the modelled interface (see Fig. 11(b)),i.e.,



|
| Fig. 11 Three-dimensional interface model |
By Eq. (37),the bonding problem can be analyzed by regarding the thickness of the interfacial layer as zero. After obtaining u, v,w,Δu,Δv,and Δw at the modelled interface,the stress components within the interfacial layer can be determined by
8 ConclusionsDifferent interface models are compared through numerical analyses, and a new interface model is developed. The main results can be concluded as follows:
(ⅰ) A cohesive model is valid only for the case that the variation of the displacement along the interface can be neglected.
(ⅱ) A cohesive model is more appropriate for soft interfacial layers. For a hard one,the spring constant may be geometry-dependent.
(ⅲ) A constitutive-based interface model is developed. No matter the interfacial layer is hard or soft,no matter the variation of the displacement along the interface is large or small,the new model can deal with them in a unified way,just by replacing the complicate interfacial layer with an equivalent homogeneous layer.
(ⅳ) The most important advantage of the new model is that it can analyze all stress components within the interfacial layer,though its thickness has been modelled as zero. The computational efficiency of the new model is the same as that of a cohesive model.
| [1] | Rizzoni, R., Dumont, S., Lebon, F., and Sacco, E. Higher order model for soft and hard elastic interfaces. International Journal of Solids and Structures, 51, 4137-4148 (2014) |
| [2] | Lebon, F. and Rizzoni, R. Asymptotic analysis of a thin interface: the case involving similar rigidity. International Journal of Engineering Science, 48, 473-486 (2010) |
| [3] | Lebon, F., Khaoua, A. O., and Licht, C. Numerical study of soft adhesively bonded joints in finite elasticity. Computational Mechanics, 21, 134-140 (1998) |
| [4] | Dundurs, J. Micromechanics and Inhomogeneity, Springer-Verlag, Berlin, 109-114 (1990) |
| [5] | Xu, J. Q. The Mechanics of Interface (in Chinese), Science Publication, Beijing (2006) |
| [6] | Benveniste, Y. A general interface model for a three-dimensional curved thin anisotropic interphase between two anisotropic media. Journal of the Mechanics and Physics of Solids, 54, 708-734 (2006) |
| [7] | Corigliano, A. Formulation, identification and use of interface models in the numerical analysis of composite delamination. International Journal of Solids and Structures, 30, 2779-2811 (1993) |
| [8] | Benveniste, Y. and Miloh, T. Imperfect soft and stiff interfaces in two-dimensional elasticity. Mechanics of Materials, 33, 309-323 (2001) |
| [9] | Elices, M., Guinea, G. V., Gomez, J., and Planas, J. The cohesive zone model: advantages, limitations and challenges. Engineering Fracture Mechanics, 69, 137-163 (2002) |
| [10] | Valoroso, N., Sessa, S., Lepore, M., and Cricri, G. Identification of mode-I cohesive parameters for bonded interfaces based on DCB test. Engineering Fracture Mechanics, 104, 56-79 (2013) |
| [11] | Özdemir, I., Brekelmans, W. A. M., and Geers, M. G. D. A thermo-mechanical cohesive zone model. Computational Mechanics, 46, 735-745 (2010) |
| [12] | Rabinovitch, O. An extended high-order cohesive interface approach to the debonding analysis of FRP strengthened beams. International Journal of Mechanical Sciences, 81, 1-16 (2014) |
| [13] | Cai, X. J. and Xu, J. Q. Interfacial fracture criteria based on the nominal deformation energy of interface. Theoretical and Applied Fracture Mechanics, 75, 16-21 (2014) |
| [14] | Yuuki, R. and Kisu, H. Elastic Analysis Based on Boundary Element Analysis, Baifukan, Tokyo (1987) |
| [15] | Bogy, D. B. Edge-bonded dissimilar orthogonal elastic wedges under normal and shear loading. Journal of Applied Mechanics, 35, 460-466 (1968) |
| [16] | Yuuki, R. and Xu, J. Q. Boundary element analysis of dissimilar materials and interface crack. Computational Mechanics, 14, 116-127 (1994) |
| [17] | Xu, J. Q., Fu, L. D., and Mutoh, Y. A method for determining elastic-plastic stress singularity at the interface edge of bonded power law hardening materials. JSME International Journal Series A, 45, 177-183 (2002) |
 2016, Vol. 37
2016, Vol. 37























































