Shanghai University
Article Information
- A. R. SETOODEH, M. REZAEI, M. R. ZENDEHDEL SHAHRI.
- Linear and nonlinear torsional free vibration of functionally graded micro/nano-tubes based on modified couple stress theory
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 725-740
- http://dx.doi.org/10.1007/s10483-016-2085-6
Article History
- Received Oct. 3, 2015;
- Revised Nov. 19, 2015
Micro/nano-tubes have been widely used in fabricate micro/nano-electromechanical systems (MEMSs/NEMSs) due to their superior properties,e.g.,transistors,semiconductors,sensor technologies,nano-oscillators,micro-electronic cooling systems,actuators,and composites[1, 2, 3].
The properties of micro/nano-tubes are closely related to their micro/nano-structures. Therefore,it is important to consider the micro/nano-scale effects. Two mainly theoretical approaches of atomistic and continuum mechanics have been used for the analyses of nano-structures. However,the atomistic method is computationally expensive,especially for large scale systems,and the classical continuum theory cannot capture the size effects which significantly affect the mechanical properties at nano-meter scales. Therefore,many non-classical continuum theories, e.g.,the couple stress theory,the nonlocal elasticity theory,and the strain gradient theory,are proposed.
Among the aforementioned theories,the classical couple stress theory is proposed and employed based on a higher-order continuum theory[4, 5, 6, 7],where two material length-scale parameters are introduced to capture the size effects in the isotropic materials. Yang et al.[8] modified the classical couple stress theory,in which only one constant was needed to take into account the size effects. The modified couple stress theory utilized an additional equilibrium relation to force the couple stress tensor to be symmetric. In recent years,many researchers have employed the modified couple stress theory to investigate the behavior of micro/nano-tubes[9, 10, 11].
A new class of composites is the functionally graded materials (FGMs),which have many applications in various industrials. These materials are inhomogeneous composites,and are commonly made from two materials. The composition and volume fraction of the materials vary with a smooth and continuous variation gradually from one surface to another. The gradient compositional variation of the constituents according to a predetermined profile causes corresponding changes in the mechanical properties of the material. One of the best advantages of FGMs is the minimization of the stress concentration that arises due to the mismatch in the elastic properties of the constituent phases. In macro-scale,many investigations have been concerned with the mechanical behavior of FGMs[12, 13, 14, 15].
Recently,FGMs have been used in micro/nano-structures and atomic force microscopes (AFMs)[16, 17, 18]. It is necessary to enhance the knowledge about the mechanical response of the FGMTs for the next technological revolution,since these structures are emerging as the new generation of the micro/nano-tubes offering exciting physical and mechanical properties. Recently,there have been some attempts to understand and explain the mechanical response of FGMTs by use of different mathematical and numerical approaches[19, 20, 21].
The torsional deformation and vibration are very common for the micro/nano-tubes subjected to the external forces in some basic components of new nano-scale devices,e.g.,oscillators, actuators,and microelectronic cooling systems. Despite the importance of this issue,only few researchers have paid attention to the torsional vibration of micro/nano-tubes. Demir and Civalek[22] investigated the size effects on the torsional and axial responses of micro-tubules by use of the nonlocal continuum rod model. Gheshlaghi and Hasheminejad[23] studied the size dependent torsional linear vibration of nano-tubes by use of the modified couple stress theory. Islam et al.[24] presented the torsional wave propagation and vibration of circular nano-structures based on Eringen’s nonlocal elasticity. Li[25] developed two different nonlocal elasticity models for the torsional vibration analyses of carbon nano-tubes according to the weakened and enhanced models. Arda and Aydogdu[26] investigated the torsional statics and dynamics of the carbon nano-tubes embedded in elastic media by use of the nonlocal elasticity theory. Lim et al.[27] developed the analytical solutions for the free torsional vibration of the circular nano-rods/tubes based on a new elastic nonlocal stress model. However,the linear or nonlinear torsional vibration of functionally graded micro/nano-tubes has not been studied.
The main target of this paper is to present an analytical solution for the linear and nonlinear torsional vibration of FGMTs by use of the modified couple stress theory,which is a non-classical theory and can capture the size effects. The homotopy analysis method (HAM) is implemented to analytically solve the related nonlinear governing equation. The material properties of the FGMTs vary continuously across the radius according to the power law distribution.
2 Modified couple stress theoryAccording to the modified couple stress theory,the strain energy U for a deformable linear elastic material occupying the volume V can be written as follows[28]:
where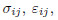 mij ,and
mij ,and 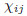 are the stress tensor,the strain tensor,the deviatoric part of the
couple stress tensor,and the symmetric curvature tensor,respectively,which are defined by
In the above equations,i,j,k = x,y,z.
are the stress tensor,the strain tensor,the deviatoric part of the
couple stress tensor,and the symmetric curvature tensor,respectively,which are defined by
In the above equations,i,j,k = x,y,z. 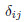 is the Kronecker delta. ui is the component of the
displacement vector. l denotes the material length scale parameter,demonstrating the couple
stress effect.
is the Kronecker delta. ui is the component of the
displacement vector. l denotes the material length scale parameter,demonstrating the couple
stress effect. 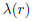 and G(r) are Lame’s constants defined by
where E(r) and
and G(r) are Lame’s constants defined by
where E(r) and 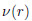 stand for Young’s modulus and Poisson’s ratio,respectively.
stand for Young’s modulus and Poisson’s ratio,respectively. 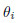 is the
component of the rotation vector obtained by
where eijk is the permutation symbol.
3 Motion equation of FGMTs
is the
component of the rotation vector obtained by
where eijk is the permutation symbol.
3 Motion equation of FGMTs
Consider an FGMT of the length L,the inner radius Ri,the outer radii Ro,the thickness
tr,the density  ,and the cross-sectional area A. The inner and outer surfaces are made of
different materials. A schematic of the geometry of the FGMT is represented in Fig. 1.
,and the cross-sectional area A. The inner and outer surfaces are made of
different materials. A schematic of the geometry of the FGMT is represented in Fig. 1.
 |
| Fig. 1 Schematic of geometry of FGMT |
In this investigation,the material properties of the tube vary continuously across the radius r according to the power law distribution as follows[20]:
The volume fraction of the materials can be written as follows:
where n is the power gradient index,and the subscripts i and o indicate the inner surface and the outer surface of the tube,respectively.The displacement field of the micro/nano-tube along the x-,y-,and z-axes can be expressed as follows[29]:
where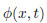 is the angular rotation about the center of the twist. The von K´arm´an straindisplacement relation with the nonlinear terms is
The strain components are obtained by substituting Eq. (10) into Eq. (11),i.e.,
The components of the rotation vector are found by expanding Eq. (7) in terms of the displacement field as follows:
The components of the curvature tensor are obtained from Eqs. (4) and (13) as follows:
Substituting Eq. (14) into Eq. (5) yields the components of the couple stress tensor as follows:
By expanding Eq. (1),the strain energy U can be written as follows:
The components of the stress field can easily be obtained by use of Eqs. (2) and (12),i.e,
Now,substituting all of the derived components of the stress tensor,the strain tensor,the
couple stress tensor,and the symmetric curvature tensor into Eq. (16) yields
where
The kinetic energy of the micro/nano-tube can be written as follows:
With the assumed displacement field,we can obtain the kinetic energy as follows:
The above equation can be simplified as follows:
where
The nonlinear vibrational governing equation of the micro/nano-tubes can be determined with
the aid of Hamilton’s principle as follows:
is the angular rotation about the center of the twist. The von K´arm´an straindisplacement relation with the nonlinear terms is
The strain components are obtained by substituting Eq. (10) into Eq. (11),i.e.,
The components of the rotation vector are found by expanding Eq. (7) in terms of the displacement field as follows:
The components of the curvature tensor are obtained from Eqs. (4) and (13) as follows:
Substituting Eq. (14) into Eq. (5) yields the components of the couple stress tensor as follows:
By expanding Eq. (1),the strain energy U can be written as follows:
The components of the stress field can easily be obtained by use of Eqs. (2) and (12),i.e,
Now,substituting all of the derived components of the stress tensor,the strain tensor,the
couple stress tensor,and the symmetric curvature tensor into Eq. (16) yields
where
The kinetic energy of the micro/nano-tube can be written as follows:
With the assumed displacement field,we can obtain the kinetic energy as follows:
The above equation can be simplified as follows:
where
The nonlinear vibrational governing equation of the micro/nano-tubes can be determined with
the aid of Hamilton’s principle as follows:
Finally,substituting Eqs. (18) and (22) into Eq. (24) and using the fundamental lemma of the variation calculus yield the nonlinear governing differential equation as follows:
In this research,the following boundary conditions are considered for the FGMTs:
(i) Both ends are fixed,i.e., = 0.
= 0.
(ii) One end is fixed,and the another end is free,i.e., = 0.
= 0.
Equation (25) is a nonlinear partial differential equation. The Galerkin method together with the separation of variables is used to solve this partial differential equation. The rotation function can be expressed as follows:
where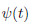 is the time dependent function that must be determined,and F(x) is defined based
on the first mode shape of the micro/nano-tube vibration for the fixed-fixed and fixed-free
boundary conditions as follows[30]:
Substituting Eq. (26) into Eq. (25),multiplying the obtained result by the function F(x),and
then integrating the governing equation over the length of the nano-tube,we have
where
In the above equations,
where the prime means differentiation with respect to x.
4.1 Analytical method
is the time dependent function that must be determined,and F(x) is defined based
on the first mode shape of the micro/nano-tube vibration for the fixed-fixed and fixed-free
boundary conditions as follows[30]:
Substituting Eq. (26) into Eq. (25),multiplying the obtained result by the function F(x),and
then integrating the governing equation over the length of the nano-tube,we have
where
In the above equations,
where the prime means differentiation with respect to x.
4.1 Analytical method
The resulted nonlinear time-dependent governing equation (29) is analytically solved by the HAM. This method does not require a small parameter in an equation,and has a significant advantage in providing an analytical approximate solution to a wide range of nonlinear problems in applied mechanics[31]. To illustrate the basic idea of the method,consider the following nonlinear time-dependent differential equation:
where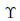 is a general differential operator,t denotes the time which is an independent variable,
and f(t) is an unknown function. Liao[31] constructed the so-called zeroth-order deformation
equation by means of generalizing the concept of homotopy as follows:
where p is the embedding parameter varying from 0 to 1,h is a nonzero auxiliary parameter,
h(t) 6≠0 is an auxiliary function,
is a general differential operator,t denotes the time which is an independent variable,
and f(t) is an unknown function. Liao[31] constructed the so-called zeroth-order deformation
equation by means of generalizing the concept of homotopy as follows:
where p is the embedding parameter varying from 0 to 1,h is a nonzero auxiliary parameter,
h(t) 6≠0 is an auxiliary function,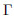 is an auxiliary linear operator,f0(t) denotes an initial guess
of f(t),and
is an auxiliary linear operator,f0(t) denotes an initial guess
of f(t),and 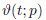 is an unknown function. It is worth noting that one has great freedom
to select the initial guess,the auxiliary linear operator,and the auxiliary function. When p
changes from zero to unity,the solution
is an unknown function. It is worth noting that one has great freedom
to select the initial guess,the auxiliary linear operator,and the auxiliary function. When p
changes from zero to unity,the solution 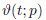 varies from the initial approximation to the
desired solution. In other words,
By differentiating Eq. (33) with respect to p,the first-order deformation equation can be obtained as follows:
Expanding
varies from the initial approximation to the
desired solution. In other words,
By differentiating Eq. (33) with respect to p,the first-order deformation equation can be obtained as follows:
Expanding 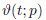 in the form of the Taylor series with respect to the parameter p,we have
where
in the form of the Taylor series with respect to the parameter p,we have
where
The above series converges at p =1 by an appropriate selection of the auxiliary linear operator,the initial guess,the auxiliary parameter,and the auxiliary function,which reads
Substituting Eq. (36) into Eq. (35),differentiating the resulting equation k times with respect to the parameter p,setting p = 0,and dividing all of the terms by k!,we can obtain the so-called kth-order deformation equation as follows:
where 4.2 Analytical resultsBy use of the transformation  in Eq. (29),the new form of the governing equation
can be obtained as follows:
in Eq. (29),the new form of the governing equation
can be obtained as follows:
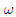 denotes the nonlinear frequency. The initial conditions are defined by
where
denotes the nonlinear frequency. The initial conditions are defined by
where 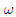 is the amplitude of the tube torsional vibration. The initial guess
is the amplitude of the tube torsional vibration. The initial guess 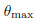 must be
selected such that the initial conditions are satisfied. Therefore,we can write a convenient
function satisfying the boundary conditions as follows:
The linear and nonlinear operators can be expressed as follows:
where
One can adjust the convergence rate of the HAM solution by means of the auxiliary parameter
must be
selected such that the initial conditions are satisfied. Therefore,we can write a convenient
function satisfying the boundary conditions as follows:
The linear and nonlinear operators can be expressed as follows:
where
One can adjust the convergence rate of the HAM solution by means of the auxiliary parameter 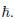 .
Liao[32] studied the influence of this parameter for different solution expressions,and exhibited
that the parameter could be selected in the range from -2 to 0 while the series converged
the fastest to the exact solution in the whole region when
.
Liao[32] studied the influence of this parameter for different solution expressions,and exhibited
that the parameter could be selected in the range from -2 to 0 while the series converged
the fastest to the exact solution in the whole region when 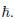 = −1. Therefore,to achieve the
accurate results by only few terms for the present problem,we set
= −1. Therefore,to achieve the
accurate results by only few terms for the present problem,we set
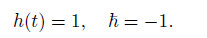
From Eqs. (45),(46),and (48),we have
subjected toSubstituting  from Eq. (44) into Eq. (49) and solving the resulted equation,we have
from Eq. (44) into Eq. (49) and solving the resulted equation,we have
The coefficient of the secular term  sin
sin  must be identical to zero since the rotation of the
micro/nano-tube is finite. Thus,
must be identical to zero since the rotation of the
micro/nano-tube is finite. Thus,
After solving Eq. (52),we can obtain the first-order approximation  for the nonlinear
frequency as follows:
for the nonlinear
frequency as follows:
Now,k should be set to be 2 in Eqs. (39) and (41) in order to obtain 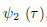 ,i.e.,
,i.e.,
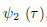 by
substituting the appropriate equations into Eq. (54),applying Eq. (56),and solving the resulted
equation,i.e.,
where
Eliminating the secular term and solving the corresponding equation,we can obtain the secondorder approximation for the nonlinear frequency as follows:
by
substituting the appropriate equations into Eq. (54),applying Eq. (56),and solving the resulted
equation,i.e.,
where
Eliminating the secular term and solving the corresponding equation,we can obtain the secondorder approximation for the nonlinear frequency as follows:
Briefly,the explicit expressions for the linear  and the nonlinear natural frequencies
and the nonlinear natural frequencies  of the FGMT with the second-order approximation can be written as follows:
of the FGMT with the second-order approximation can be written as follows:
Eventually,the HAM solution to the third-order approximation can be obtained by collecting the resulted terms as follows:
The dimensionless linear and nonlinear natural frequencies can be defined,respectively,as follows: where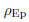 and EEp are,respectively,the density and Young’s modulus of the epoxy,respectively.
5 Numerical examples
and EEp are,respectively,the density and Young’s modulus of the epoxy,respectively.
5 Numerical examples
In this stage,some numerical results are presented to demonstrate the reliability and the efficiency of the developed analytical expressions. The obtained explicit relations in the previous section are used to study the linear and nonlinear torsional free vibration responses of FGMTs. The tubes with fixed-fixed and fixed-free boundary conditions are considered. Due to the lack of experimental data,the length scale parameter l is assumed to be 17.6 mm,which is reported for the epoxy. The non-dimensional form of the length scale parameter is used in the present work for the sake of generality. The material length scale parameter is mathematically the square root of the ratio of the modulus of the curvature to the modulus of the shear,and is physically a property of measuring the couple stress effect. This parameter can be found from the torsion tests of the slim cylinders with different diameters or the bending tests of the thin beams with different thicknesses. To determine the length scale parameter for a specific material,some classic experiments such as the micro-bending test,the micro-torsion test,and the specially micro/nano-indentation test have been be performed[33]. The geometric properties of the tubes are
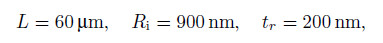
Due to the lack of the similar solution concerning the problem of the torsional vibration of
FGMTs in the open literature,the accuracy of the present solution is verified by comparing the
results with those of Ref. [23] (see Tables 1 and 2). The geometrical parameters are considered
to be identical to the values reported in Ref. [23] when L = 30 mm,Ro = 900 nm,Ri = 200 nm.
Gheshlaghi and Hasheminejad[23] investigated the torsional free vibration of fixed-fixed nanotubes,and reported the size dependency of the corresponding natural frequencies by use of the
couple stress theory. They defined a dimensionless linear frequency parameter by the ratio of the
non-classical linear natural frequency to the classical linear natural frequency,which we denote
here by  . To demonstrate the efficacy of the model,the natural frequencies corresponding
to the higher modes of vibration are determined by changing the value of the parameter m in
Eq. (27). Table 1 shows the variations of the parameter
. To demonstrate the efficacy of the model,the natural frequencies corresponding
to the higher modes of vibration are determined by changing the value of the parameter m in
Eq. (27). Table 1 shows the variations of the parameter  in terms of the dimensionless length
scale parameter (l/Ro) for the first mode (m = 1) as well as the 100th mode (m = 100). It is
seen that the results of the proposed method agree with those of Ref. [23]. The developed results
exhibit that the size effect has a significant effect on the dimensionless frequency parameter,
and this effect increases when the vibration modes increase. Moreover,the effects of the inner
radius to the outer radius ratio (Ri/Ro) on the frequency parameter
in terms of the dimensionless length
scale parameter (l/Ro) for the first mode (m = 1) as well as the 100th mode (m = 100). It is
seen that the results of the proposed method agree with those of Ref. [23]. The developed results
exhibit that the size effect has a significant effect on the dimensionless frequency parameter,
and this effect increases when the vibration modes increase. Moreover,the effects of the inner
radius to the outer radius ratio (Ri/Ro) on the frequency parameter  for the first mode and
the 25th mode are illustrated in Table 2. It is seen that the numerical results agree well with
each other.
for the first mode and
the 25th mode are illustrated in Table 2. It is seen that the numerical results agree well with
each other.
 for fixed-fixed micro/nano-tube
for fixed-fixed micro/nano-tube  |
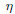 for
fixed-fixed micro/nano-tube
for
fixed-fixed micro/nano-tube  |
Without loss of generality,we assume here that the FGMT is made of aluminum (Al) and
epoxy (Ep) with the properties as follows: EAl = 70GPa, = 0.23,
= 0.23, = 2 700 kg/m3,
EEp = 1.44GPa,
= 2 700 kg/m3,
EEp = 1.44GPa, = 0.38,and
= 0.38,and  = 1 220 kg/m3.
= 1 220 kg/m3.
The convergence study of the solution in predicting the dimensionless nonlinear torsional
natural frequencies versus the amplitude of the vibration for fixed-fixed FGMTs are demonstrated in Table 3. The first-,second-,and third-order approximations for the non-dimensional
nonlinear frequencies are obtained and shown,respectively,with  . From the table,
we can see that the convergence rate of the results is fast. To exhibit the discrepancy among the
classical stress theory,the couple stress theory,and the linear and nonlinear vibration analyses
for FGMTs,we depict the variations of different frequencies versus the dimensionless length
scale parameter l/Ro in Fig. 2. According to the trend of the results,the importance of performing a nonlinear or even a linear non-classical analysis for the torsional vibration of FGMTs
is evident. This verifies the size-dependency of the natural frequencies of FGMTs.
. From the table,
we can see that the convergence rate of the results is fast. To exhibit the discrepancy among the
classical stress theory,the couple stress theory,and the linear and nonlinear vibration analyses
for FGMTs,we depict the variations of different frequencies versus the dimensionless length
scale parameter l/Ro in Fig. 2. According to the trend of the results,the importance of performing a nonlinear or even a linear non-classical analysis for the torsional vibration of FGMTs
is evident. This verifies the size-dependency of the natural frequencies of FGMTs.
 |
 |
Fig. 2 Dimensionless natural frequencies of fixed-fixed FGMTs as function of length scale parameter,
where n = 2, m = 1, and  = 0.01 = 0.01  |
The dimensionless nonlinear torsional natural frequencies versus the vibration amplitude for fixed-fixed and fixed-free FGMTs are,respectively,shown in Figs. 3(a) and 3(b). Different values of the dimensionless length scale parameter are considered. From the figures,we can see that, when the vibration amplitude increases,the nonlinearity of the system increases,leading to the enhancement of the dimensionless nonlinear frequency. According to the developed results, the effect of the dimensionless material length scale parameter decreases when the vibration amplitude increases. Also,it is revealed that the dimensionless nonlinear natural frequency increases when the dimensionless material length scale parameter increases. Moreover,the results exhibit that the natural frequencies predicted for the fixed-fixed boundary condition are higher than those obtained for the micro/nano-tubes with fixed-free end conditions. In fact, the fixed-fixed nano-tubes have higher stiffness in comparison with that of the fixed-free tubes, and therefore the frequencies are enhanced.
 |
| Fig. 3 Effects of dimensionless length scale parameter on dimensionless nonlinear natural frequency versus vibration amplitude for fixed-fixed and fixed-free FGMTs, where n = 1 |
In Fig. 4,the effects of the material gradient index on the dimensionless nonlinear frequency versus the vibration amplitude for the fixed-fixed and fixed-free boundary conditions are shown. The dimensionless material length scale parameter is considered to be l/Ro = 0.5. The developed results demonstrate that the dimensionless nonlinear natural frequency of the micro/nanotubes decreases by increasing the power law index. It means that the results shift from the natural frequency of the metallic micro/nano-tubes towards the epoxy one. The enhancement rate of the dimensionless nonlinear frequency increases with the decrease in the material gradient index for both the fixed-fixed condition and fixed-free boundary condition. However,this rate is magnified for the case of fixed-free FGMTs.
 |
| Fig. 4 Effects of material gradient index n on dimensionless nonlinear frequency versus vibration amplitude for fixed-fixed and fixed-free FGMTs, where l/Ro = 0.5 |
The effects of the material gradient index on the dimensionless nonlinear natural frequencies versus the vibration amplitude for two distinct values of the non-dimensional length scale parameter and the different boundary conditions are demonstrated in Fig. 5. It is observed that the size effect contribution on the dimensionless fundamental frequency significantly increases when the material gradient index decreases. The variations of the dimensionless response of FGMTs versus the time with two distinct values of the vibration amplitude are shown in Fig. 6, where l/Ro = 0.5,and n = 2.
 |
| Fig. 5 Effects of material gradient index n on dimensionless nonlinear natural frequency versus vibration amplitude for fixed-fixed and fixed-free FGMTs, where l/Ro = 0.1, and l/Ro = 0.25 |
 |
| Fig. 6 Variations of non-dimensional response of fixed-fixed FGMTs versus dimensionless time with vibration amplitude, where l/Ro = 0.5, and n = 2 |
The linear and nonlinear torsional free vibration analyses of functional gradient micro/nanotubes are analytically studied on the basis of the modified couple stress theory. Hamilton’s principle is used to obtain the nonlinear non-classical governing equation of motion. To examine the effect of the boundary conditions,two types of end conditions,i.e.,fixed-fixed and fixedfree,are considered. The present model accounts for the material length scale parameter and the two-constituent material variation through the radius of the micro/nano-tubes. The HAM is used to analytically solve the corresponding nonlinear differential equation. The developed explicit expressions for the nonlinear natural frequencies can be conveniently implemented to investigate the effects of different parameters such as the length scale,the material gradient index,and the vibration amplitude on the natural frequencies. To exhibit the accuracy,efficacy, and efficiency of the analytical solution,some numerical results are presented.
The main conclusions are summarized as follows:
(i) The results exhibit that the size effect has a significant effect on the dimensionless linear and nonlinear frequencies,and this effect increases when the vibration modes are higher.
(ii) According to the developed results,the importance of performing a non-classical analysis for the linear and nonlinear torsional vibrations of FGMTs is evident.
(iii)When the vibration amplitude increases,the nonlinearity of the system increases,leading to the enhancement of the dimensionless nonlinear frequency.
(iv) The dimensionless nonlinear natural frequency increases when the dimensionless length scale parameter increases.
(v) The natural frequencies predicted for the fixed-fixed boundary condition are higher than those obtained for the tubes with the fixed-free end conditions.
(vi) The enhancement rate of the dimensionless frequency increases when the material gradient index decreases for both the fixed-fixed boundary condition and the fixed-free boundary condition.
| [1] | Fennimore, A. M., Yuzvinsky, T. D., Han, W. Q., Fuhrer, M. S., Cumings, J., and Zettl, A. Rotational actuators based on carbon nano-tubes. nature, 424, 408-410 (2003) |
| [2] | Najmzadeh, M., Haasl, S., and Enoksson, P. A. Silicon straight tube fluid density sensor. Proceedings of IEEE Sensors, 17, 1185-1188 (2007) |
| [3] | Hao, P. F., Zhang, X. W., Yao, Z. H., and He, F. Transitional and turbulent flow in a circular micro-tube. Experimental Thermal and Fluid Science, 32, 423-431 (2007) |
| [4] | Toupin, R. A. Elastic materials with couple-stresses. Archive for Rational Mechanics and Analysis, 11, 385-414 (1962) |
| [5] | Mindlin, R. D. and Tiersten, H. F. Effects of couple-stresses in linear elasticity. Archive for Rational Mechanics and Analysis, 11, 415-448 (1962) |
| [6] | Koiter, W. T. Couple-stresses in the theory of elasticity: Ⅰ and Ⅱ. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Series B, 67, 17-44 (1964) |
| [7] | Peng, X. W., Guo, X. M., Liu, L., and Wu, B. J. Scale effects on nonlocal buckling analysis of bilayer composite plates under non-uniform uniaxial loads. Applied Mathematics and Mechanics (English Edition), 36(1), 1-10 (2015) DOI 10.1007/s10483-015-1900-7 |
| [8] | Yang, F., Chong, A. C. M., Lam, D. C. C., and Tong, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39, 2731-2743 (2002) |
| [9] | Ke, L. L. and Wang, Y. S. Flow-induced vibration and instability of embedded double-walled carbon nano-tubes based on a modified couple stress theory. Physica E: Low-Dimensional Systems and Nanostructures, 43, 1031-1039 (2011) |
| [10] | Wang, L. Size-dependent vibration characteristics of fluid-conveyingmicro-tubes. Journal of Fluids and Structures, 26, 675-684 (2010) |
| [11] | Yang, T. Z., Ji, S. D., Yang, X. D., and Fang, B. Micro-fluid-induced nonlinear free vibration of micro-tubes. International Journal of Engineering Science, 76, 47-55 (2014) |
| [12] | Malekzadeh, P. and Beni, A. A. Free vibration of functionally graded arbitrary straight-sided quadrilateral plates in thermal environment. Composite Structures, 92, 2758-2767 (2010) |
| [13] | Malekzadeh, P., Shahpari, S. A., and Ziaee, H. R. Three-dimensional free vibration of thick functionally graded annular plates in thermal environment. Journal of Sound and Vibration, 329, 425-442 (2010) |
| [14] | Selahi, E., Setoodeh, A. R., and Tahani, M. Three-dimensional transient analysis of functionally graded truncated conical shells with variable thickness subjected to an asymmetric dynamic pressure. International Journal of Pressure Vessels and Piping, 119, 29-38 (2014) |
| [15] | Akgöz, B. and Civalek, Ö. Shear deformation beam models for functionally graded micro-beams with new shear correction factors. Composite Structures, 112, 214-225 (2014) |
| [16] | Witvrouw, A. and Mehta, A. The use of functionally graded poly-SiGe layers for MEMS applications. Materials Science Forum, 492-493, 255-260 (2005) |
| [17] | Lee, Z., Ophus, C., Fischer, L. M., Nelson-Fitzpatrick, N., Westra, K. L., Evoy, S., Radmilovic, V., Dahmen, U., and Mitlin, D. Metallic NEMS components fabricated from nano-composite Al-Mo films. Nanotechnology, 17, 3063-3070 (2007) |
| [18] | Rahaeifard, M., Kahrobaiyan, M., and Ahmadian, M. Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials. ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, ASME, San Diego, 539-544 (2009) |
| [19] | Setoodeh, A. R. and Afrahim, S. Nonlinear dynamic analysis of FG micro-pipes conveying fluid based on strain gradient theory. Composite Structures, 116, 128-135 (2014) |
| [20] | Janghorban, M. and Zare, A. Free vibration analysis of functionally graded carbon nano-tubes with variable thickness by differential quadrature method. Physica E: Low-Dimensional Systems and Nanostructures, 43, 1602-1604 (2011) |
| [21] | Ke, L. L., Wang, Y. S., Yang, J., and Kitipornchai, S. Nonlinear free vibration of size-dependent functionally graded micro-beams. International Journal of Engineering Science, 50, 256-267 (2012) |
| [22] | Demir, Ç. and Civalek, Ö. Torsional and longitudinal frequency and wave response of microtubules based on the nonlocal continuum and nonlocal discrete models. Applied Mathematical Modelling, 37, 9355-9367 (2013) |
| [23] | Gheshlaghi, B. and Hasheminejad, S. M. Size dependent torsional vibration of nano-tubes. Physica E: Low-Dimensional Systems and Nanostructures, 43, 45-48 (2010) |
| [24] | Islam, Z. M., Jia, P., and Lim, C. W. Torsional wave propagation and vibration of circular nanostructures based on nonlocal elasticity theory. International Journal of Applied Mechanics, 6, 1450011 (2014) |
| [25] | Li, C. Torsional vibration of carbon nano-tubes: comparison of two nonlocal models and a semicontinuum model. International Journal of Mechanical Sciences, 82, 25-31 (2014) |
| [26] | Arda, M. and Aydogdu, M. Torsional statics and dynamics of nano-tubes embedded in an elastic medium. Composite Structures, 114, 80-91 (2014) |
| [27] | Lim, C. W., Li, C., and Yu, J. L. Free torsional vibration of nano-tubes based on nonlocal stress theory. Journal of Sound and Vibration, 331, 2798-2808 (2012) |
| [28] | Kong, S. L., Zhou, S. J., Nie, Z. F., and Wang, K. The size-dependent natural frequency of Bernoulli-Euler micro-beams. International Journal of Engineering Science, 46, 427-437 (2008) |
| [29] | Rao, S. S. and Yap, F. F. Mechanical Vibrations, Addison-Wesley, New York (1995) |
| [30] | Rao, S. S. Vibration of Continuous Systems, John Wiley & Sons, New Jersey (2007) |
| [31] | Liao, S. J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, Ph.D. dissertation, Shanghai Jiao Tong University (1992) |
| [32] | Liao, S. J. Beyond Perturbation: Introduction to the Homotopy Analysis Method, Chapman & Hall/CRC Press, Boca Raton (2004) |
| [33] | Park, S. K. and Gao, X. L. Bernoulli-Euler beam model based on a modified couple stress theory. Journal of Micromechanics and Microengineering, 16, 2355-2359 (2006) |
 2016, Vol. 37
2016, Vol. 37



























































