Shanghai University
Article Information
- Shaopu YANG, Xueqian FANG, Jianchao ZHANG, Dujuan WANG.
- Dynamic behavior of bridge-erecting machine subjected to moving mass suspended by wire ropes
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 741-748
- http://dx.doi.org/10.1007/s10483-016-2087-6
Article History
- Received Oct. 20, 2015;
- Revised Nov. 27, 2015
2. China Railway Engineering Equipment Group Co., Ltd., Zhengzhou 453000, China
Bridge erecting machines have been extensively used in bridge engineering owing to its high efficiency and convenience. Nowadays,a permanent tendency towards improving the performances of these machines,including strength and stability,is attracting more and more interests. To identify the root reasons of the accident in the process of construction,it is of great significance to investigate the dynamic response of bridge erecting machines.
Bridge erecting machines are regarded as flexible structures. Regardless of the geometrical differences,almost all machines from this class of equipments are exposed to the effects of a working load whose basic characteristic is relative to the support structure of the machine[1]. The flexible structures are often modelled as beams or plates. Identifying the behavior of the beams or plates under dynamic loads is an extremely important stage in the design. A thorough and sophisticated identification of the dynamic behavior creates a basis for avoiding failures, damages,and serious accidents,which may inevitably lead to very high financial losses and present at the same time a potential serious risk to the workers’ safety. The free vibration problem of a beam or plate carrying any number of concentrated masses has been widely investigated. However,because of the complexity of the mathematical expressions,only the beams or plates carrying one or two concentrated masses have been dealt with in the literatures. Greco and Santini[2] studied the dynamic vibration of a uniform simply supported beam subjected to a constant moving loading,and attached two rotational viscous dampers at the ends of the beam. Yanmeni et al.[3] investigated the nonlinear dynamic behavior of a Euler-Bernoulli beam under moving loads. Mart´ınez-Castro et al.[4] studied the response of the Bernoulli-Euler beam to a unit load circulating at a constant speed of the train,and considered the effect of the viscous modal damping. Simsek and Kocat¨urk[5] presented a geometrically nonlinear dynamic analysis of an eccentrically prestressed simply supported damped beam subjected to a concentrated moving harmonic load,and obtained the nonlinear dynamic deflections of the beam by polynomial functions. Garinei[6] studied the vibration of a simple beam-like modelled bridge traversed by a concentrated moving load that varied during the transit time. Sudheesh et al.[7] investigated the dynamic behaviors of simply supported uniform beams subjected to a moving point load,and formulated a simple closed-form expression for the free vibration response.
The problem of a flexible beam carrying a moving mass is a fundamental problem in the design of machining processes. However,it is still very difficult to be solved. For the beam system, the moving mass is an excitation source,which may be very complex[8]. In transportation engineering applications,the excitation source,such as the motion of vehicles on bridges,cranes carrying moving loads,robotic arms,and space structures,is often encountered. To solve this kind of problems,new methods should be introduced. Zrni´c et al.[9] used the combined finite element and analytical method to study the dynamic responses of a gantry crane structure subjected to the moving load with suspension elements in such a system. For the bridge-erecting machine subjected to a moving mass suspended by wire ropes,the excitation source results in a complex partial differential equation. This problem has not been dealt with.
The purpose of this paper is to use the analytical-and-numerical-combined method to determine the vibration responses for a uniform simple beam carrying a moving mass suspended by wire ropes. The equation of motion for the simple beam is derived by replacing the moving mass suspended by the wire ropes with a massless spring-damper-mass system,and the effective spring constant and the damper coefficient of the system are derived. With the effective constants of the excitation source and the expansion method,the solution of vibration is obtained. Through the numerical examples,the effects of the material properties of the ropes,the frequency of the excitation source,and the dimension of the beam are analyzed in detail. To confirm the reliability of the presented theory,the simplified results obtained from the paper are compared with the corresponding results obtained in other literatures.
2 Problem descriptionA bridge-erecting machine is modelled by a simple beam,and the length of beam is L (see Fig. 1). The beam carries a sudden applied load through a wire rope,and the moving speed of the load is V. The load suspended by a wire rope is modelled by a spring-damper-mass system with arbitrary magnitudes.
 |
| Fig. 1 Uniform simple beam carrying spring-damper-mass system |
Neglecting the effects of the shear deformation and rotary inertia,the vertical deflection w(x,t) of the simply supported beam under the action of a time-dependent load P(t) can be described by
where E is Young’s modulus of elasticity,I is the inertia moment,m is the mass per unit length of the beam,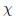 is the damping coefficient of the beam,w(x,t) is the transverse deflection of the
beam at the attaching point located position x and the time t,and P(t) is the interactive force
between the spring-damper-mass system and the beam.
is the damping coefficient of the beam,w(x,t) is the transverse deflection of the
beam at the attaching point located position x and the time t,and P(t) is the interactive force
between the spring-damper-mass system and the beam. 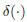 is the Dirac delta function. H(t)
is the Heaviside unit function,which is introduced to define the suddenly applied load,i.e.,
is the Dirac delta function. H(t)
is the Heaviside unit function,which is introduced to define the suddenly applied load,i.e.,
The initial and boundary conditions are expressed as follows[2]:
where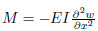 is the bending moment of the beam.
is the bending moment of the beam.
The equation of motion for the spring-damper-mass system alone is given by
or where u(t),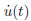 ,and
,and 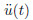 are the displacement,the velocity,and the acceleration of the concentrated
mass m0 with respect to its static equilibrium position,respectively (see Fig. 1).
are the displacement,the velocity,and the acceleration of the concentrated
mass m0 with respect to its static equilibrium position,respectively (see Fig. 1). 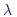 and f are the damping coefficient and the spring constant of the spring-damper-mass system,
respectively.
3 Replaced spring-damper-mass system with effective constants
and f are the damping coefficient and the spring constant of the spring-damper-mass system,
respectively.
3 Replaced spring-damper-mass system with effective constants
Using the eigenfunction expansion method,the transverse deflection of the beam satisfying the boundary conditions can be expressed as follows:
where qn(t) is the nth generalized coordinate,and N is the total number of the considered modes.From Eq. (6),we can obtain the transverse deflection of the beam at the position x = xe as follows:
An exciting force with the form of P(t) =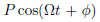 is assumed. Then,the following
equation for the time-dependent generalized coordinates can be obtained:
where
is assumed. Then,the following
equation for the time-dependent generalized coordinates can be obtained:
where 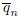 is the amplitude of qn(t),
is the excitation frequency,and i =
is the amplitude of qn(t),
is the excitation frequency,and i = 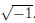 .
.
Substituting Eq. (8) into Eq. (7),one can obtain
Combining Eqs. (5) and (9),we can obtain the particular solution of u(t) as follows:
where u0 is the amplitude of u(t).Then,we can obtain
From Eq. (14),we can obtainSubstituting Eqs. (11)-(15) into Eq. (4),we have the following relation:
where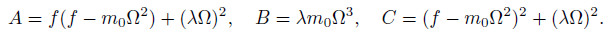
Substituting Eq. (16) into Eq. (4),we have
where 4 Deflection under moving harmonic loadSince the effective spring constant fe and the effective damping coefficient  are derived,the
vibration responses of the simple beam can be determined by conventional numerical methods.
are derived,the
vibration responses of the simple beam can be determined by conventional numerical methods.
Combining Eqs. (1),(6),and (17),the following equation can be obtained:
where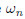 is the square of the natural frequency for the nth mode given by
is the square of the natural frequency for the nth mode given by
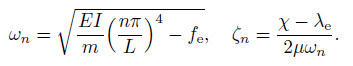
 is the transit frequency.
is the transit frequency.
With the initial conditions in Eq. (2),the solution of Eq. (20) can be written as follows:
where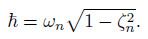
Combining Eqs. (21) and (22),one can obtain
where In the above equation, 5 Analysis of dynamic responseThe purpose of the following study is to point out those aspects that have importance in evaluating the combined effects of the moving load suspended by a rope. According to the character of a simple beam,the deflection at the midpoint should be the maximum. Therefore, only the deflection at the midpoint is analyzed in the following numerical examples. The amplification of the deflection at the midpoint qn(t) is normalized by Q(t) = qn(t)/q0,and q0 = 2PL3/(π4EI) is the deflection corresponding to the static load at the midpoint. The input parameters for the bridge-erecting machine and the load are illustrated in Table 1.
Figure 2 shows the amplification Q(t) under different frequencies of the load. For the bridgeerecting machine with a span of 30m,the fundamental frequency is about 5Hz. It can be seen that the vibration amplification increases with the load frequency if the load frequency is less than 5.0. The vibration amplification is the maximum when the load frequency is 5.0. These conclusions are consistent with those in Ref. [7]. It should be noted that the time for reaching the maximum amplification is less when the excitation frequency is 5.0.
 |
Fig. 2 Amplification at midpoint of simple
beam under harmonic load, where
f = 0, L = 30, and  = 0 = 0 |
Figure 3 shows the amplification Q(t) under different spring constants of the rope. In
this figure,the load frequency is low. If the sprint constant is larger than 1.0,the vibration
amplification will decrease when the spring constants of the rope increase. If the sprint constants
are smaller than 1.0,the vibration amplification will be very small. The maximum amplification
in the case
 = 5.0 is about ten times of that in the case
= 5.0 is about ten times of that in the case
 = 1.0.
= 1.0.
 |
Fig. 3 Amplification at midpoint of simple
beam under harmonic load suspended
by rope, where
 = 1, L =
30, and = 1, L =
30, and  = 0.2 = 0.2 |
Figure 4 shows the amplification Q(t) under different spring constants of the rope (
 = 5.0).
Considering the results in Fig. 3,we can obtain that a larger sprint constant of the rope should
be designed to obtain a small amplification.
= 5.0).
Considering the results in Fig. 3,we can obtain that a larger sprint constant of the rope should
be designed to obtain a small amplification.
 |
Fig. 4 Amplification at midpoint of simple
beam under harmonic load, where
 = 5, L = 30, and = 5, L = 30, and  = 0.2 = 0.2 |
Figure 5 shows the amplification Q(t) under different spring constants of the rope (
 = 8.0).
It can be seen that the maximum amplification occurs at f = 20.0,and the time for reaching
the maximum amplification increases significantly. The amplification in the case f = 20.0 is
about five times of that in the case f = 5.0. It can be concluded that the spring constant of the
rope can change the fundamental frequency of the beam under the high frequency of loadings.
= 8.0).
It can be seen that the maximum amplification occurs at f = 20.0,and the time for reaching
the maximum amplification increases significantly. The amplification in the case f = 20.0 is
about five times of that in the case f = 5.0. It can be concluded that the spring constant of the
rope can change the fundamental frequency of the beam under the high frequency of loadings.
 |
Fig. 5 Amplification at midpoint of simple
beam under harmonic load, where
 = 8, L = 30, and = 8, L = 30, and  = 0.2 = 0.2 |
Figure 6 illustrates the effects of the length of the beam on the amplification Q(t). In this figure,the length of the beam is L = 20m. It can be seen that the maximum amplification of the deflection is small. However,the variation of the deflection with time increases significantly. The effect of the spring constant of the rope on the amplification is smaller if the length of the beam becomes small.
 |
Fig. 6 Amplification at midpoint of simple
beam under harmonic load, where
 = 2, L = 20, and = 2, L = 20, and  = 0.2 = 0.2 |
Figure 7 illustrates the effects of the damping coefficient of the rope on the amplification Q(t). It can be seen that the effects of the damping coefficient of the rope on the amplification are very little.
 |
Fig. 7 Amplification at midpoint of simple
beam under harmonic load, where
 = 2, L = 20, and f = 10 = 2, L = 20, and f = 10 |
Combining the expanded method and the effective spring-damper-mass system method,the dynamic responses of a bridge-erecting machine subjected to a moving mass which is suspended by wire ropes are obtained. The numerical results show that each improvement in the machine performances should be accompanied with a strong dynamical analysis because of the strong dynamic effects of the parameters of the structure and loading. With appropriate rope parameters, the amplification of the deflection can be reduced significantly. The effects of the rope characters on the deflection of the beams vary with the applied load frequencies. The damping of the ropes can slightly affect the vibration amplitudes of the displacements. If the beam is short,the effects of the rope characters will decrease.
| [1] | Ding, H. J., Chen, W. Q., and Xu, R. On the bending, vibration and stability of laminated rectangular plates with transversely isotropic layers. Applied Mathematics and Mechanics (English Edition), 22(1), 17-24 (2001) DOI 10.1007/BF02437941 |
| [2] | Greco, A. and Santini, A. Dynamic response of a flexural non-classically damped continuous beam under moving loadings. Computers and Structures, 80, 1945-1953 (2002) |
| [3] | Yanmeni, A. N., Tchoukuegno, R., and Woafo, P. Non-linear dynamics of an elastic beam under moving loads. Journal of Sound and Vibration, 273, 1101-1108 (2004) |
| [4] | Martínez-Castro, A. E. Museros, P., and Castillo-Linares, A. Semi-analytic solution in the time domain for non-uniform multi-span Bernoulli-Euler beams traversed by moving loads. Journal of Sound and Vibration, 294, 278-297 (2006) |
| [5] | Simsek, M. and Kocatürk, T. Nonlinear dynamic analysis of an eccentrically prestressed damped beam under a concentrated moving harmonic load. Journal of Sound and Vibration, 320, 235-253 (2009) |
| [6] | Garinei, A. Vibrations of simple beam-like modelled bridge under harmonic moving loads. International Journal of Engineering Science, 44, 778-787 (2006) |
| [7] | Sudheesh, C. P., Sujatha, C., and Shankar, K. Vibration of simply supported beams under a single moving load: a detailed study of cancellation phenomenon. International Journal of Mechanical Sciences, 99, 40-47 (2015) |
| [8] | Majumder, L. and Manohar, C. S. A time-domain approach for damage detection in beam structures using vibration data with a moving oscillator as an excitation source. Journal of Sound and Vibration, 268, 699-716 (2003) |
| [9] | Zrnić, N. D., Gaćić, V. M., and Boćnjak, S. M. Dynamic responses of a gantry crane system due to a moving body considered as moving oscillator. Archives of Civil and Mechanical Engineering, 15, 243-250 (2015) |
 2016, Vol. 37
2016, Vol. 37























