Shanghai University
Article Information
- Tao LI, Jingxia SUI, Chuijie WU.
- Numerical investigation of dynamical behavior of tethered rigid spheres in supersonic flow
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 749-760
- http://dx.doi.org/10.1007/s10483-016-2090-6
Article History
- Received Jan. 14, 2016;
- Revised Jan. 16, 2016
2. School of Energy and Power Engineering, Dalian University of Technology, Dalian 116024, Liaoning Province, China
The space tethered system has a wide range of applications in various space missions[1]. One application is the use of electrodynamic tethers in carrying electric current,which can generate thrust or drag from a planetary magnetic field in a space debris removal mission. The generated thrust can be used to decelerate space debris,and thus produce the earlier reentry of parts of the debris into Earth’s atmosphere. Moreover,a momentum exchange tether can be used as a drag device during the deorbiting of a reentry capsule to reduce the heat loads on the capsule[2]. We are interested in the dynamical behavior of the tethered system in a supersonic flow,which has not been mentioned in the literature.
Laurence and Deiterding[3] and Laurence et al.[4] investigated the dynamical separation behavior of bodies without tethers,and studied two spheres with different radius ratios and initial configurations in a Mach-4 flow. They concluded that the qualitative separation behavior and the final lateral velocity of the smaller sphere varied strongly with both the radius ratio and the initial alignment angle of the two spheres. Li et al.[5] investigated the rotational effects on the dynamical separation behavior of the bodies,and found that the rotary motion could extend the time of “surfing” and made the final lateral velocity of separation bigger. The present work is based on the above discoveries. The schematic configuration considered in this work is presented in Fig. 1. Two spheres with different radius ratios,i.e.,r2/r1 = 0.625 and r2/r1 = 1,and different length tethers,i.e.,l/r1 = 2,3,4,+∞,are considered. The two spheres,centroid axially aligned,are held stationary first,then released,and subsequently let fly freely in a Mach-4 flow.
 |
| Fig. 1 Schematic diagram of two spheres with tethers in supersonic flow, where r1 is radius of bigger sphere, and r2 is radius of smaller sphere |
In this paper,the spheres are considered to be rigid with non-ablating bodies. The tether is slender. We ignore its influence on the flow field. The Favre-filtered Navier-Stokes equations are considered. In our opinion,the Euler equations are for far field,and are not suitable for near field. We may note that the first grid cells at the wall are too coarse to capture the details of the subcell motion. Therefore,the usual no-slip boundary condition is no longer appropriate,and must be replaced by another condition. One approach is using a wall model. However,the pressure forces on the bluff bodies behind a detached and normal-shock-type wave front are usually so high that the skin friction and/or boundary-layer effects are comparatively small and may be neglected[6]. Therefore,the viscous force applied on the bodies is neglected in this investigation. A reflect boundary condition is used to enforce the immersed boundary conditions. This work is based on the AMROC-WENO-TCD/VTF code (http://www.cacr.caltech.edu/asc). For readers’ convenience,we give a brief description of the computational modelling. The structure of this paper is as follows. In Section 2,the computational modelling is described. The computational overview of the investigation is presented in Section 3. The validation and results of the investigation are presented and discussed in Section 4 and Section 5,respectively. Finally, some conclusions are drawn in Section 6.
2 Computational modelling 2.1 Fluid solverTo investigate the dynamical behavior of the rigid spheres with a tether interacting with a supersonic flow,a fluid solver for the three-dimensional and Favre-filtered compressible NavierStokes equations in the Cartesian coordinates to a rigid body solver coupled with the consideration of the Newtonian laws of motion are employed. The conservation law form governing equations of the fluid flow are written as follows:
where q(x,t) is the vector of the state defined by and fn(q) is the flux function defined by Here,the subscript n is the nth component of the variables,and n = 1,2,3. The variables with overlines are box-filtered variables,and the variables with wide tildes are Favre-filtered variables. ρ is the density. t is the time. u is the the velocity. p is the hydrostatic pressure. δ is the Kronecker delta. E is the total energy per mass unit.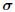 is the viscous stress tensor
defined by
is the viscous stress tensor
defined by
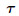 is the subgrid stress tensor defined by
is the subgrid stress tensor defined by
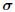 e is the subgrid total energy defined by
q is the heat conduction,which follows the Fourier law as follows:
where κ is the air conductivity.
e is the subgrid total energy defined by
q is the heat conduction,which follows the Fourier law as follows:
where κ is the air conductivity.
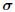 e is a variable,which needs to be modelled. In the AMROC-WENO-TCD code,the
stretched-vortex subgrid model proposed by Kosovi´c et al.[7],Misra and Pullin[8],and Pullin[9]
is implemented to model
e is a variable,which needs to be modelled. In the AMROC-WENO-TCD code,the
stretched-vortex subgrid model proposed by Kosovi´c et al.[7],Misra and Pullin[8],and Pullin[9]
is implemented to model 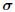 e. Besides,the equation of state is also required to be close to the
above system of equations,i.e.,
e. Besides,the equation of state is also required to be close to the
above system of equations,i.e.,
Equation 1 is approximated in the explicit finite-volume scheme as follows:
where the subscript i is the ith component of the variables,and i = 1,2,3. The superscript ν is the step number for the time advance in a computational period,and ν = 1,2,3.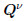 is
the conservative variable obtained within a computational period. Qn (n = 0,1,2,· · · ) is the
conservative variable obtained in the previous computational period. The iteration is started
with ν = 1,and n = 0. F is the numerical flux function. α,β, and γ are the coefficients
listed in Table 1. The viscous terms of F are computed by an explicit,centered,second-order,
and 3-point stencil scheme. The inviscid terms of F are computed first by the Steger-Warming
flux vector splitting method[10] and then by the third-order weighted essentially non-oscillatory
(WENO) scheme[11] to interpolate the flux values on the cell boundaries. An optimal thirdorder
strong stability-preserving (SSP) Runge-Kutta scheme is used to evolve the time step of
the system.
is
the conservative variable obtained within a computational period. Qn (n = 0,1,2,· · · ) is the
conservative variable obtained in the previous computational period. The iteration is started
with ν = 1,and n = 0. F is the numerical flux function. α,β, and γ are the coefficients
listed in Table 1. The viscous terms of F are computed by an explicit,centered,second-order,
and 3-point stencil scheme. The inviscid terms of F are computed first by the Steger-Warming
flux vector splitting method[10] and then by the third-order weighted essentially non-oscillatory
(WENO) scheme[11] to interpolate the flux values on the cell boundaries. An optimal thirdorder
strong stability-preserving (SSP) Runge-Kutta scheme is used to evolve the time step of
the system.
In this investigation,the surfaces of spheres are moving immersed boundaries for the flow solver. The ghost fluid method[12] in conjunction with the level set method[13] are used,where the nearest layers of the cells within the spheres are ghost cells. The width of the ghost cells depends on the stencil of the Eulerian solver. Besides,an automatic dynamic mesh adaptation along the moving immersed boundary is used since this approach usually reduces the approximation accuracy on the boundary. A two-dimensional immersed boundary treatment schematic diagram on a Cartesian grid in the literature[14] is shown in Fig. 2.
 |
| Fig. 2 Two-dimensional schematic of immersed boundary treatment in Ref. [14], where BI is abbre- viation of boundary intercept point, MP is abbreviation of mirror point, and shadow zones denote bilinear interpolation stencils |
Once the ghost cells are determined,the coordinates of their corresponding MPs will be calculated. Then,a bilinear interpolation procedure (three-dimensional trilinear) is used to calculate the values at these MPs. For the Dirichlet boundary condition,it can be enforced by setting the value at the ghost cells (φGC) as follows:
where φBI is the value at the boundary intercept between the ghost cell and the MP. For the Neumann boundary condition,it can be enforced by setting φGC as follows: where Δl denotes the distance between the ghost cell and the MP. 2.3 Adaptive mesh refinementSince the simulations in this investigation are three-dimensional and the computation domain should be large enough to allow the spheres to fly free,the computational cost is huge. To reduce this,the adaptive mesh refinement technology is used in the AMROC-WENO/TCD (adaptive mesh refinement in object-oriented C++) code[15].
The regions near the immersed boundaries,where shock exists,must be refined. To do this, we need to chose an appropriate refinement criterion. In this investigation,we do the refinement at the cells whenever
where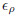 is the threshold value (0.04 in this paper) for the adaptive refinement. In addition,8
coarser cells near the boundaries are refined too.
2.4 Coupling algorithm
is the threshold value (0.04 in this paper) for the adaptive refinement. In addition,8
coarser cells near the boundaries are refined too.
2.4 Coupling algorithm
To treat the communications between the fluid solver and the rigid body solver,two types of coupling strategies are developed,i.e.,the loose-coupling algorithm and the strong-coupling algorithm. The main difference between the two strategies is how the rigid body solver integrates in the time[16, 17, 18]. The loose-coupling algorithm integrates in the time explicitly,while the strong-coupling algorithm integrates in the time implicitly. The loose-coupling algorithm has a faster computational speed but with lower stability. The main issue affecting its stability is the so-called “added mass” effect[19]. In this investigation,the density ratio of the fluid-to-sphere is very small,which ensures the stability of the loose-coupling algorithm. Therefore,we choose the loose-coupling algorithm. In this approach,the solution at the next time step n + 1 is determined as follows:
(i) The force f on each body consists of three components,i.e.,the aerodynamic force fa, the tether pulling force ft,and the collision force fc. fa is calculated by integrating the pressure over the surface of sphere. ft is calculated by |ft| = kΔl/l,where k is the coefficient of elasticity (10 000N·m−1 in this paper),and l and Δl are the length of the tether and the increment of the tether,respectively. Assume that the perfect elastic collision |fc| is 1 000N,which is much greater than any other force.
(ii) The coordinates of each sphere’s center (x) is updated according to the Newtonian laws of motion as follows:
where m is the mass of the sphere.(iii) The level-set function is updated,and the fluid solver advances a time step.
3 Computational overviewWe consider a supersonic flow with a free-stream Mach number M∞ = 4,driving two spheres with different radius ratios,initially stationary,then centroid axially aligned,with an identical tether,and finally flying freely. An ideal gas is assumed for the free stream. We specify the air properties as follows: ρa = 0.07 kg · m−3,μ = 1.73 × 10−5 Pa · s,γ = 1.4, and k = 0.025 7W· m−1 · K−1,where ρa is the density,μ is the viscosity coefficient,γ is the ratio of the specific heats,and k is the thermal conductivity coefficient. The uniform initial conditions are ρ0 = ρa,u0 = 0m· s,and p0 = 1 400 Pa. The left boundary of the computational domain is an inflow boundary,where ρi = ρa,pi = p0,and ui = (670,0,0)m · s. Other sides of the computational domain are outflow boundaries. We specify the properties of the bodies as follows: ρs = 1 122 kg · m−3,and r1 = 0.025m,where ρs is the density,and the radius ratio r2/r1 is chosen to be 0.625 and 1,respectively,which will make the smaller sphere experience different types of motion,namely,“surfing” on the bow shock generated by the bigger sphere or being rapidly expelled from the region[3, 4] bounded by the shock. The tether length varies from 2r1 to 4r1,and the x-velocity of the spheres are denoted as vx1 and vx2,respectively.
The computation is separated into two parts. When t < 1×10−5 s,the inflow velocity at the left-side is continuously increased by specifying ui (1−exp(−5×10−5)). When t > 1×10−5 s, ui = 670m·s−1. The spheres are held to be stationary during the interval t ∈ [0,0.001 4] s,which will establish a quasi-steady flow field. When t > 0.001 4 s,the spheres are allowed to fly freely. The level of the adaptive mesh refinement is set to be two,and the minimal spatial resolution is Δmin = 0.001 m. The time step is calculated according to the Courant-Friedrichs-Lewy (CFL) condition number,and the maximum CFL number is set to be 0.85.
4 ValidationTo validate the present simulation,we compare the numerical results with the experimental data[4]. In the experiment,Laurence et al.[4] investigated the dynamical behavior of two spheres with different radius ratios. Here,we study the same configuration as them. Two simulations are performed to qualitatively and quantitatively compare the results. Both simulations use a computational domain of the size [−0.05,0.025]m × [−0.095,0.145]m × [−0.09,0.09]m and a base grid of the size 150× 120× 90 with two-level adaptive mesh refinement (AMR). The final simulation time is te = 0.024 s. Other computational details can be found in Section 3.
First,a qualitative comparison of the flow fields is performed. The radii of the two stationary spheres are r1 = 0.025 4 m and r2 = 0.015 875 m,and their center coordinates are initially located at (0m,0m,0m) and (0m,0.043 275m,0m),respectively. Figure 3(a) is a schlieren image obtained through the introduction of a horizontal knife edge in Ref. [4],and Fig. 3(b) is a computational pseudo-schlieren image generated by visualize the magnitude of the density gradients on the z = 0 plane. The flow structures agree each other well.
 |
| Fig. 3 Comparison of schlieren image from experiment in Ref. [4] with computed pseudo-schlieren image, where r2/r1 = 0.5 |
Next,we perform a qualitative comparison of the computational results with experimental data. The radii of the two stationary spheres are r1 = 0.025 m and r2 = 0.012 7m,and their center coordinates are initially located at (0m,0m,0m) and (0m,0.040 1m,0m),respectively. The following dimensionless variables are defined:
where t′ is the dimensionless time,x′ and y′ are the dimensionless distances,v′x and v′y are the dimensionless velocities,and CD and CL are the drag coefficient and the lift coefficient, respectively. V = 670 m·s−1 is the inlet velocity. The subscripts x and y are the directions of the coordinate frame. x(0) and y(0) are the initial x- and y-coordinates of the bigger sphere, respectively. a and v are the instantaneous acceleration and velocity. r is the radius.Figure 4 compares the obtained non-dimensional displacements,velocities,drag coefficients, and lift coefficients of the two spheres with the experimental data. From the figure,we can see that,although the results generally agree with each other (especially the results of the bigger sphere),the computational lateral velocity of the smaller sphere decreases earlier than that in the experiment (t′ = 2.5). This means that the smaller sphere in our simulation is entrained earlier in the flow region bounded by the primary bow shock than in the experiment. This is due to the different manners of releasing the spheres. In our simulations,the instant when the spheres are released is precisely specified. In contrast,the corresponding instant in the experiment cannot be well defined. It is not surprise that the force coefficients during the startup period do not agree with those in the experiment,since the flow conditions are not strictly the same. As shown in Figs. 4(c)-4(d),the computational velocities are held to be zero during the interval t′ ∈ (0,0.291),while the computational velocities in the experiment are nonzero. This difference is amplified in the next period,finally leading to a different “entrainment time”. Once the smaller sphere is entrained in the flow region bounded by the primary bow shock,the drag coefficients and lift coefficients rapidly decrease. Considering that the force coefficients of the smaller sphere are substantially more sensitive to the spheres’ relative positions,the force coefficients exhibit good overall agreement.
 |
Fig. 4 Experimental and computational results for two spheres freely separated, where r2/r1 = 0.5,
blue  denotes computational point when small sphere is entrained in flow region bounded
by primary bow shock, and big blue • denotes corresponding experimental point
denotes computational point when small sphere is entrained in flow region bounded
by primary bow shock, and big blue • denotes corresponding experimental point |
In this subsection,we treat two spheres as a system,and investigate their centroidal quantities. We use a computational domain of the size [−0.07m,0.73m]×[−0.2m,0.2 m]×[−0.2m, 0.2m] and the base grids 200 × 100 × 100 with three-level AMR. The radius of one sphere is fixed to be r1 = 0.025m,and the radius of the other sphere is set to be r2 = 0.4r1,r2 = 0.625r1, and r2 = r1,respectively. The length of the tether l is set to be l = 2r1,l = 3r1,and l = 4r1, respectively,in the different simulations. Their centers are initially located at (0,−r1,0) and (0,r2,0),respectively. When the spheres reach the boundaries of the computational domain, the simulation is terminated. The maximum final simulation time is set to be tmax = 0.08 s. For more computational details,see Section 3.
The following dimensionless variables are defined:
where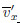 is the dimensionless mean x-velocity of the system which also called the lengthwise
velocity,
is the dimensionless mean x-velocity of the system which also called the lengthwise
velocity,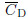 is the drag coefficient of the system,and ax1 and ax2 are the instantaneous accelerations
of the two spheres. Other dimensionless variables used in this section are the same as
those in Section 4.
is the drag coefficient of the system,and ax1 and ax2 are the instantaneous accelerations
of the two spheres. Other dimensionless variables used in this section are the same as
those in Section 4.
Now,we demonstrate the types of motion that the system experiences. Figure 5 plots the pressure contours on the central plane,z = 0m,for six different types of motion. In Figs. 6(b) and 6(d),we label the types of motion only for the r2 = 0.625r1,l = 2r1 case and the r2 = r1,l = 3r1 case because all the cases for the same radius ratio experience similar types of movements. We note that the drag coefficient increases for the r2 = 0.625r1 cases at the beginning of the changes compared with the no-tether case. This is because that the tether will force the smaller sphere to move downward to the bigger sphere and make the higher pressure region move upward from its lower-left direction (see Fig. 5(a)),resulting in the increase in the drag of the system. We denote this type motion as “Type A”. Following the “Type A” motion, the second sphere will be entrained into the region bounded by the primary shock,which results in less drag. This type of motion is denoted as “Type B” (see Fig. 5(b)). When the smaller sphere reaches the lower shock front,it is dragged along the shock (see Fig. 5(c)). This type of motion is denoted as “Type C”,and will increase the drag experienced by the system. The action mechanism is similar to that of the “Type A” motion. Note that there may be a type of motion whereby the smaller sphere is thrown out of the region bounded by the shock generated by the bigger sphere for another radius ratio case.
 |
| Fig. 5 Six different types of motion, where images show pressure contours on central plane (z = 0m), straight red dashed lines denote stretched tether, curved red dashed lines denote relaxed tether, and black arrows denote direction of velocity of smaller sphere relative to bigger sphere: (a)– (c) r2 = 0.625r1, and l = 3r1; 6(d)–6(f) r2 = r1, and l = 3r1 |
 |
| Fig. 6 System quantities for different r2 and l, where dashed lines in (d) are octuple y distance between two spheres for each case, Type A, Type B, Type C, Type E, and Type F are motion types defined in Fig. 5 |
For the r2 = r1 case,the x positions of the two spheres are approximately equal. Therefore, the tether only constrains their relative y positions. The decrease in the system drag coefficient is due to another reason. Because the velocities of the spheres are small compared with the free stream (the maximum is approximately 3%) during the entire simulation,we can ignore the influence of the changes in the velocity,and determine the system drag coefficients only by their relative positions. In Fig. 6(d),we denote the octuple y distance between the two spheres for each case by dashed lines. Note that the drag coefficients are strongly related to the y distance between the two spheres. When the y distance between the two spheres increases,the drag coefficients decrease,and vice versa,expect for the coefficients during t′ ∈ [0,2.5] compared with the l = 3r1 case for t′ ∈ [4,9] and the l = 4r1 case for t′ ∈ [8,12]. This is because that the flow conditions have not yet reached the steady state for t′ ∈ [0,2.5] (see Fig. 5(d)). This type of motion is denoted as “Type D” (see Fig. 5(e)),and the steady flow situation is denoted as “Type F”(see Fig. 5(f)).
For the r2 = 0.625r1 cases,the system experiences “Type A” motion,then “Type B” motion,and then “Type C” motion,subsequently repeating this process until the system decays or becomes unstable. During the process,the mean x velocities of the system will increase, decrease,and finally increase. After one period of motion,the x velocities of the system decrease compared with the no-tether system. For the r2 = r1 system,the motion will alternate between “Type E” motion and “Type F” motion until the system becomes unstable and makes the x-velocity of the system increase compared with the no-tether system.
Because the x-velocity is the quantity of the principal interest here,in Fig. 6,we compare the normalized x-velocity and the drag coefficient of the system for seven configurations,which have varying radius ratios and tether lengths. General speaking,for all r2 = 0.625r1 cases with a tether,the mean normalized x-velocity decreases compared with the no-tether case (l = +∞), and the l = 2r1 case reduces the maximum. Moreover,For all the r2 = r1 cases with a tether, the normalized x-velocity increases. In general,this is caused by the different relative positions of the spheres after the tether is tensioned. For the r2 = 0.625r1 cases,the tether stretches the smaller sphere into the wake region bounded by the primary bow shock,which makes the system experience a smaller drag. In contrast,for the r2 = r1 cases,the tether stretches the two spheres closer,which increases the windward of the system and produces a greater drag.
5.2 Quantities of bigger sphereIn this subsection,we discuss the quantities concerning the bigger sphere. Our principal interest is the x-velocity of the sphere,i.e.,vx. Figure 7 shows the profiles of vx and the drag coefficient versus the non-dimensional time for different cases. From the figure,we can see that vx increases in all cases but with different mechanisms.
 |
| Fig. 7 Normalized x-velocity and drag coefficient of bigger sphere for different cases |
From Figs. 7(a) and 7(b),we can see that the x-velocity of the bigger sphere experiences a greater acceleration than in the no-tether case when the tether is stretched. This is because that the smaller sphere always flies faster than the bigger sphere. However,the tether pulls the two spheres closer when r2 = r1,which makes each sphere experience greater drag,resulting in the increase in the x-velocity of the bigger sphere over that of the no-tether case. From Figs. 6(e) and 6(f),we can see that the closer spheres experience a greater drag than the remote spheres. From Figs. 7(b) and 7(d),we can see that every time the two spheres collide,the drag coefficient of the bigger sphere peaks. For the r2 = r1 cases,this is because that the centroids of the spheres are not strictly aligned along the y-axis. This may cause the system to become unstable and the motion type to change. The peaks in Figs. 7(b) and 7(d) are caused by the collision of the two spheres.
6 ConclusionsWe have performed a series of numerical simulations to investigate the dynamical behavior characteristics of two spheres with various configurations in a supersonic flow. The quantities concerning both the system and the bigger sphere are investigated. The results can be summarized as follows:
(i) There are at least six types of motion in the system. Each type of motion exhibits a different drag coefficient.
(ii) Compared with the no-tether case,the change in the mean stream-wise velocity of the tethered system depends on the radius ratio of the spheres. For equally sized spheres,the velocity increases. In contrast,the velocity decreases for unequally sized spheres.
(iii) For all cases,the stream-wise velocity of the bigger sphere increases but with different mechanisms. This property can be used to design the decelerators for re-entry devices.
| [1] | Chen, Y., Huang, R., Ren, X., He, L., and He, Y. History of the tether concept and tether missions: a review. ISRN Astronomy and Astrophysics, 2013, 502973 (2013) |
| [2] | Kornuta, J. A. and Guo, S. Momentum exchange tether as a hypersonic parachute during reentry for human missions. Journal of Spacecraft and Rockets, 47, 571-579 (2010) |
| [3] | Laurence, S. J. and Deiterding, R. Shock-wave surfing. Journal of Fluid Mechanics, 676, 396-431 (2011) |
| [4] | Laurence, S. J., Parziale, N. J., and Deiterding, R. Dynamical separation of spherical bodies in supersonic flow. Journal of Fluid Mechanics, 713, 159-182 (2012) |
| [5] | Li, T., Sui, J. X., Gong, S., and Wu, C. J. Dynamical separation of rigid bodies in supersonic flow. Science China: Technological Sciences, 58, 1-12 (2015) |
| [6] | Hoerner, S. Fluid Dynamic Drag: Practical Information on Aerodynamic Drag and Hydrodynamic Resistance, Hoerner Fluid Dynamics, Bakersfield (1965) |
| [7] | KosoviÇ, B., Pullin, D. I., and Samtaney, R. Subgrid-scale modeling for large-eddy simulations of compressible turbulence. Physics of Fluids, 14, 1511-1522 (2002) |
| [8] | Misra, A. and Pullin, D. I. A vortex-based subgrid stress model for large-eddy simulation. Physics of Fluids, 9, 2443-2454 (1997) |
| [9] | Pullin, D. I. A vortex-based model for the subgrid flux of a passive scalar. Physics of Fluids, 12, 2311-2319 (2000) |
| [10] | Steger, J. L. and Warming, R. Flux vector splitting of the inviscid gasdynamic equations with application to finite-difference methods. Journal of Computational Physics, 40, 263-293 (1981) |
| [11] | Liu, X. D., Osher, S., and Chan, T. Weighted essentially non-oscillatory schemes. Journal of Computational Physics, 115, 200-212 (1994) |
| [12] | Fedkiw, R. P., Aslam, T., Merriman, B., and Osher, S. A non-oscillatory eulerian approach to interfaces in multimaterial flows (the ghost fluid method). Journal of Computational Physics, 152, 457-492 (1999) |
| [13] | Wu, K., Hao, L., Wang, C., and Zhang, L. Level set interface treatment and its application in Euler method. Science China: Physics, Mechanics and Astronomy, 53, 227-236 (2010) |
| [14] | Mittal, R., Dong, H., Bozkurttas, M., Najjar, F., Vargas, A., and von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. Journal of Computational Physics, 227, 4825-4852 (2008) |
| [15] | Deiterding, R. Detonation structure simulation with amroc. High Performance Computing and Communications, Springer, Heidelberg, 916-927 (2005) |
| [16] | Lee, X. and Lee, C. An implicit algorithm based on iterative modified approximate factoriza-tion method coupling with characteristic boundary conditions for solving subsonic viscous flows. Science China: Physics, Mechanics and Astronomy, 56, 1187-1208 (2013) |
| [17] | Bai, Y., Yang, K., Sun, D., Zhang, Y., Kennedy, D., Williams, F., and Gao, X. Numerical aerodynamic analysis of bluff bodies at a high reynolds number with three-dimensional CFD modelling. Science China: Physics, Mechanics and Astronomy, 56, 277-289 (2013) |
| [18] | Borazjani, I., Ge, L., and Sotiropoulos, F. Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. Journal of Computational Physics, 227, 7587-7620 (2008) |
| [19] | Conca, C., Osses, A., and Planchard, J. Added mass and damping in fluid-structure interaction. Computer Methods in Applied Mechanics and Engineering, 146, 387-405 (1997) |
 2016, Vol. 37
2016, Vol. 37



















