Shanghai University
Article Information
- S. A. SHEHZAD, F. M. ABBASI, T. HAYAT, B. AHMAD.
- Cattaneo-Christov heat flux model for third-grade fluid flow towards exponentially stretching sheet
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 761-768
- http://dx.doi.org/10.1007/s10483-016-2088-6
Article History
- Received Oct. 11, 2015;
- Revised Feb. 17, 2016
2. Department of Mathematics, Comsats Institute of Information Technology, Islamabad 44000, Pakistan;
3. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan;
4. NAAM Research Group, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia
Researchers at present have interest to explore the phenomenon of non-Newtonian liquids over the stretching surface. It is all due to the practical implementations of non-Newtonian materials in industry and technology. Most of liquids used in our daily routine exhibit the characteristics of non-Newtonian liquids. Examples of such liquids include shampoos,soaps, apple sauce,muds,sugar solution,condensed milk,tomato ketchup,etc. The boundary layer behavior of non-Newtonian materials over a moving surface has extensive applications in plastic sheet manufacturing,fiber spinning,petroleum drilling,aerodynamic construction of plastic films,glass blowing,continuous casting and so on. All non-Newtonian materials cannot be evaluated by a single relation. Different fluid models have been formulated for different nonNewtonian materials according to their nature. The model of third-grade fluids is amongst such non-Newtonian materials that explore the shear thinning and shear thickening effects. Sahoo and Poncet[1] addressed the effect of the viscous dissipation in the stretched flow of thirdgrade liquid by imposing the slip conditions at the surface. Here,the heat transfer analysis is made for both constant and variable surface temperature conditions. Abbasbandy and Hayat[2] developed the homotopic algorithm of the time-dependent special third-grade fluid induced by a porous sheet. Hayat et al.[3] examined the temperature stratification effect in the thermally radiative flow of a third-grade fluid past a stretching sheet. Hussain et al.[4] explored the effect of Ohmic heating in the two-dimensional (2D) flow of a third-grade fluid in the presence of nanoparticles. Sajid et al.[5] reported the axisymmetric flow of a third-grade fluid induced by a thin lubricated surface.
Heat transfer phenomena occur in many engineering and industrial applications,e.g.,heat pumps,heat conduction in tissues,energy creation,and copper materials. Due to such importance,Fourier[6] derived the heat conduction law to examine the mechanism of the heat transfer in various objects. Cattaneo[7] developed the modified version of Fourier’s law of heat conduction,and considered the relaxation time effect to avoid the paradox of heat conduction. Christov[8] employed Oldroyd’s upper convective derivative to introduce the material invariant formula for the Maxwell-Cattaneo law. Straughan[9, 10] explored the heat transfer analysis in porous and thermal convections by using the Cattaneo heat flux formula. Tibullo and Zampoli[11] presented the unique solutions of the Cattaneo-Christov heat equation for an incompressible liquid. Haddad[12] addressed the thermal instability of the Cattaneo-Christov model for Brinkman porous medium problems. Han et al.[13] reported the stretched flow of a Maxwell fluid with the Cattaneo-Christov heat flux model under the slip condition. Khan et al.[14] numerically investigated the Cattaneo-Christov heat flux model for the steady flow of a viscoelastic fluid induced by an exponentially stretching. Hayat et al.[15] explored the effect of homogenous and heterogeneous reactions in the 2D flow of a non-Newtonian fluid with the Cattaneo-Christov heat flux theory. Abbasi et al.[16] presented the optimal homotopic solutions of an Oldroyd-B fluid by considering the Cattaneo-Christov heat flux model.
The theme of this article is to explore the effect of the Cattaneo-Christov heat flux model in the 2D laminar flow of a third-grade fluid induced by an exponentially stretched surface. In the literature,the heat transfer analysis of a third-grade fluid has been reported by employing the simple Fourier’s law of heat conduction. Here,we utilize the Cattaneo-Christov heat flux theory. The presence of the thermal relaxation factor corresponds to an increase in the nonlinearity of energy expression. To tackle this highly nonlinear problem,we employ the homotopic criteria[17, 18, 19, 20, 21, 22, 23] for the series solutions. The obtained series solutions are plotted graphically and discussed physically.
2 Mathematical developmentLet us assume the 2D laminar flow of a third-grade fluid due to an exponentially stretching sheet. The laws of the conservation and linear momentum have the following forms for the present flow configuration[1]:
The boundary conditions are where u and v denote the velocity components parallel to the x- and y-directions,respectively, α1*,α2* ,and α3* are the material parameters,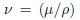 is the kinematic viscosity,μ is the
dynamic viscosity,ρ is the density of the fluid,U0 is the reference velocity,and L is the
reference length.
is the kinematic viscosity,μ is the
dynamic viscosity,ρ is the density of the fluid,U0 is the reference velocity,and L is the
reference length.
The Cattaneo-Christov heat flux model can be written as follows[7, 13]:
where q is the heat flux,λ2 is the relaxation time of the heat flux,T is the temperature,k is the thermal conductivity,and V is the velocity vector. Fourier’s law of heat conduction can be obtained by setting λ = 0. The law of energy conservation can be expressed byThen,the governing energy expression becomes
The boundary conditions for energy equation are where α denotes the thermal diffusivity,Tw is the temperature at the wall,T∞ is the ambient fluid temperature,and T0 is the reference temperature.The equations (2),(3),(6),and (7) can be reduced to dimensionless forms by introducing the following new variables[1, 14]:
The equations of momentum and energy can be reduced to where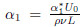 is the viscoelastic parameter,
is the viscoelastic parameter,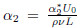 is the cross-viscous parameter,
is the cross-viscous parameter,
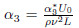 is the third-grade parameter,De = λc is the Deborah number with respect to the
relaxation time of the heat flux,and
is the third-grade parameter,De = λc is the Deborah number with respect to the
relaxation time of the heat flux,and 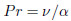 is the Prandtl number.
3 Analysis and discussion
is the Prandtl number.
3 Analysis and discussion
The solutions of Eqs. (9) and (10) along with the boundary conditions (11) and (12) are
obtained through the homotopy analysis method (HAM). This method consists of the auxiliary
parameters  and
and  that are very useful for adjusting and controlling the convergence. The
proper values of these parameters are obtained by plotting the
that are very useful for adjusting and controlling the convergence. The
proper values of these parameters are obtained by plotting the 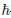 -curves at the 12th-order of
approximations (see Fig. 1). From Fig. 1,we can see that the suitable values of
-curves at the 12th-order of
approximations (see Fig. 1). From Fig. 1,we can see that the suitable values of 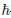 f ,
f ,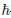 g,and
g,and 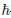 θ
are −1.40≤
θ
are −1.40≤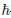 f≤0.20,−1.30≤
f≤0.20,−1.30≤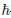 g≤0.40,and≤1.00≤
g≤0.40,and≤1.00≤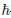 θ≤0.25. The residual errors of
functions f(η) and θ(η) are plotted in Figs. 2 and 3,respectively,to obtain the optimal values
of
θ≤0.25. The residual errors of
functions f(η) and θ(η) are plotted in Figs. 2 and 3,respectively,to obtain the optimal values
of 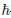 f and
f and 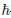 θ. The convergent values of f′′(0) and θ′(0) at different orders of computations are
explored in Table 1 when α1 = 0.3,α2 = 0.2 = β,Pr = 1.0,A = 0.5,and
θ. The convergent values of f′′(0) and θ′(0) at different orders of computations are
explored in Table 1 when α1 = 0.3,α2 = 0.2 = β,Pr = 1.0,A = 0.5,and 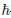 f = −0.50 =
f = −0.50 = 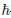 θ.
From Table 1,we can see that the values of θ′(0) in the case of Fourier’s law of heat conduction
are smaller than those obtained by the Cattaneo-Christov heat flux. This guarantees that the
24th-order solutions correspond to the convergent solutions.
θ.
From Table 1,we can see that the values of θ′(0) in the case of Fourier’s law of heat conduction
are smaller than those obtained by the Cattaneo-Christov heat flux. This guarantees that the
24th-order solutions correspond to the convergent solutions.
 |
Fig. 1 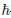 -curves for f′′(0) and θ′(0) at 12th-
order of HAM deformations when
α1 = 0.3, α2 = 0.2 = β = De,
Pr = 1.0, and A = 0.5 -curves for f′′(0) and θ′(0) at 12th-
order of HAM deformations when
α1 = 0.3, α2 = 0.2 = β = De,
Pr = 1.0, and A = 0.5 |
 |
| Fig. 2 Residual error for f(η) when α1 = 0.3, α2 = 0.2 = β = De, Pr = 1.0, and A = 0.5 |
 |
| Fig. 3 Residual error for θ(η) when α1 = 0.3, α2 = 0.2 = β = De, Pr = 1.0, and A = 0.5 |
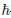 f = −0.50 =
f = −0.50 = 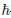 θ
θ  |
Figures 4 and 5 elaborate the variations in the dimensionless velocity f′(η) and the temperature θ(η) for several values of the viscoelastic parameter α1. From these curves,we can see that the velocity field and the momentum boundary layer thickness increase while the temperature profile and the thermal boundary layer thickness reduce when the viscoelastic parameter increases. Physically,when the viscoelastic parameter increases,the elastic deformation of the fluid increases,due to which the velocity distribution function increases whereas the temperature distribution function decreases. The effects of the cross-viscous parameter α2 on the fluid velocity and temperature are investigated in Figs. 6 and 7,respectively. It is clearly observed from these figures that both the velocity field and the temperature profile have quite reverse behaviors when the cross-viscous parameter increases. The increase in the cross-viscous parameter leads to a reduction in the velocity profile while increases in the temperature and its associated boundary layer thickness.
 |
| Fig. 4 Effects of α1 on f′(η) when α2 = 0.2 = β, and De = 0.3 |
 |
| Fig. 5 Effects of α1 on θ(η) when α2 = 0.2 = β, De = 0.3, Pr = 1.0, and A = 0.5 |
 |
| Fig. 6 Effects of α2 on f′(η), where β = 0.2, and α1 = 0.3 = De |
 |
| Fig. 7 Effects of α2 on θ(η), where β = 0.2, α1 = 0.3 = De, Pr = 1.0, and A = 0.5 |
The effects of the Deborah number De on the temperature profile θ(η) are investigated in Fig. 8. From the figure,we can see that the increase in De creates decreases in the temperature profile and the thermal boundary layer thickness. The heat flux relaxation time is stronger for larger De. Such stronger heat flux relaxation time is responsible for the lower temperature and thinner thermal boundary layer thickness. The Cattaneo-Christov heat flux theory can be reduced to Fourier’s law of heat conduction by setting De = 0. Figure 9 shows the curves of the temperature profile for various values of the Prandtl number Pr. Here,we observe that lower Prandtl number corresponds to higher temperature. The temperature decreases when we enhance the values of the Prandtl number. The Prandtl number is inversely related to the thermal diffusion parameter. Larger Pr corresponds to weaker thermal diffusion,resulting in smaller temperature and thinner thermal boundary layer (see Fig. 9). The changes in the temperature θ(η) for different values of the parameter A are shown in Fig. 10. An increase in A leads to decreases in the temperature and its associated thermal boundary layer thickness.
 |
| Fig. 8 Effects of De on θ(η), where α2 = 0.2 = β, α1 = 0.3, Pr = 1.0, and A = 0.5 |
 |
| Fig. 9 Effects of Pr on θ(η), where α2 = 0.2 = β, α1 = 0.3 = De, and A = 0.5 |
 |
| Fig. 10 Effects of A on θ(η), where α2 = 0.2 = β, α1 = 0.3 = De, and Pr = 1.0 |
The salient features of the Cattaneo-Christov heat flux model for an incompressible flow of a third-grade fluid are investigated. The flow generation is due to an exponential stretching of the sheet. We have seen that the values of θ′(0) are smaller for Fourier’s law of heat conduction while the values of θ′(0) are larger for the Cattaneo-Christov heat flux theory. When the viscoelastic parameter α1 increases,the fluid velocity and the boundary layer thickness increase,while the temperature and the thermal boundary layer thickness decrease. The presence of the crossviscous parameter α2 leads to a reduction in the velocity field and momentum boundary layer thickness. The temperature profile and thermal boundary layer thickness decrease when De increases. The Cattaneo-Christov model corresponds to the case of simple Fourier’s law when the heat flux relaxation time is zero. Larger Pr yields lower temperature and thinner thermal boundary layer thickness. This phenomenon is due to the involvement of the thermal diffusion.
| [1] | Sahoo, B. and Poncet, S. Flow and heat transfer of a third-grade fluid past an exponentially stretching sheet with partial slip boundary condition. International Journal of Heat and Mass Transfer, 54, 5010-5019 (2011) |
| [2] | Abbasbandy, S. and Hayat, T. On series solution for unsteady boundary layer equations in a special third-grade fluid. Communications in Nonlinear Science and Numerical Simulation, 16, 3140-3146 (2011) |
| [3] | Hayat, T., Shehzad, S. A., Qasim, M., Asghar, S., and Alsaedi, A. Thermally stratified radiative flow of third-grade fluid over a stretching surface. Journal of Thermophysics and Heat Transfer, 28, 155-161 (2014) |
| [4] | Hussain, T., Hayat, T., Shehzad, S. A., Alsaedi, A., and Chen, B. A model of solar radiation and Joule heating in flow of third-grade nanofluid. Zeitschrift fjr Naturforschung A, 70, 177-184 (2015) |
| [5] | Sajid, M., Ahmad, M., Ahmad, I., Taj, M., and Abbasi, A. Axisymmetric stagnation-point flow of a third-grade fluid over a lubricated surface. Advances in Mechanical Engineering, 7, 1-8 (2015) |
| [6] | Fourier, J. B. J. Théorie Analytique de la Chaleur, Chez Firmin Didot, Paris (1822) |
| [7] | Cattaneo, C. Sulla conduzione del calore. Atti del Seminario Matematico e Fisico dell'Universit`a di Modena, 3, 83-101 (1948) |
| [8] | Christov, C. I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mechanics Research Communications, 36, 481-486 (2009) |
| [9] | Straughan, B. Porous convection with Cattaneo heat flux. International Journal of Heat and Mass Transfer, 53, 2808-2812 (2010) |
| [10] | Straughan, B. Thermal convection with the Cattaneo-Christov model. International Journal of Heat and Mass Transfer, 53, 95-98 (2010) |
| [11] | Tibullo, V. and Zampoli, V. A uniqueness result for the Cattaneo-Christov heat conduction model applied to incompressible fluids. Mechanics Research Communications, 38, 77-79 (2011) |
| [12] | Haddad, S. A. M. Thermal instability in Brinkman porous media with Cattaneo-Christov heat flux. International Journal of Heat and Mass Transfer, 68, 659-668 (2014) |
| [13] | Han, S., Zheng, L., Li, C., and Zhang, X. Coupled flow and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model. Applied Mathematics Letters, 38, 87-93 (2014) |
| [14] | Khan, J. A., Mustafa, M., Hayat, T., and Alsaedi, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLoS One, 10, e0137363 (2015) |
| [15] | Hayat, T., Imtiaz, M., Alsaedi, A., and Almezal, S. On Cattaneo-Christov heat flux in MHD flow of Oldroyd-B fluid with homogeneous-heterogeneous reactions. Journal of Magnetism and Magnetic Materials, 401, 296-303 (2016) |
| [16] | Abbasi, F. M., Mustafa, M., Shehzad, S. A., Alhuthali, M. S., and Hayat, T. Analytical study of Cattaneo-Christov heat flux model for a boundary layer flow of Oldroyd-B fluid. Chinese Physics B, 25, 014701 (2016) |
| [17] | Zheng, L., Wang, L., and Zhang, X. Analytic solutions of unsteady boundary flow and heat transfer on a permeable stretching sheet with non-uniform heat source/sink. Communications in Nonlinear Science and Numerical Simulation, 16, 731-740 (2011) |
| [18] | Liao, S. J. Homotopy Analysis Method in Nonlinear Differential Equations, Higher Education Press, Beijng (2012) |
| [19] | Turkyilmazoglu, M. Solution of the Thomas-Fermi equation with a convergent approach. Com-munications in Nonlinear Science and Numerical Simulation, 17, 4097-4103 (2012) |
| [20] | Zheng, L., Zhang, C., Zhang, X., and Zhang, J. Flow and radiation heat transfer of a nanofluid over a stretching sheet with velocity slip and temperature jump in porous medium. Journal of Franklin Institute, 350, 990-1007 (2013) |
| [21] | Abbasbandy, S., Hayat, T., Alsaedi, A., and Rashidi, M. M. Numerical and analytical solutions for Falkner-Skan flow of MHD Oldroyd-B fluid. International Journal of Numerical Methods for Heat and Fluid Flow, 24, 390-401 (2014) |
| [22] | Hayat, T., Hussain, T., Shehzad, S. A., and Alsaedi, A. Flow of an Oldroyd-B fluid with nanopar-ticles and thermal radiation. Applied Mathematics and Mechanics (English Edition), 36, 69-80 (2015) DOI 10.1007/s10483-015-1896-9 |
| [23] | Shehzad, S. A., Hayat, T., Alsaedi, A., and Ahmad, B. Effects of thermophoresis and thermal radiation in mixed convection three-dimensional flow of Jeffrey fluid. Applied Mathematics and Mechanics (English Edition), 36, 655-668 (2015) DOI 10.1007/s10483-015-1935-7 |
 2016, Vol. 37
2016, Vol. 37










