2016, Vol. 37
Shanghai University
Article Information
- Chibin ZHANG, Xiaohui LIN, Hao YANG.
- Theoretical model of biomacromolecule through nanopore including effects of electrolyte and excluded volume
- Appl. Math. Mech. -Engl. Ed., 2016, 37(6): 787-802
- http://dx.doi.org/10.1007/s10483-016-2082-6
Article History
- Received Aug. 21, 2015;
- Revised Oct. 29, 2015
The translocation process of biomacromolecule through nanopores is a common and significant biological phenomenon widely existing in biology,medicine,and pharmacology,e.g.,the transportation of viral genome,the translocation of ribonucleic acid (RNA) through nuclear pore complexes,the translocation of protein through the mitochondria,and the transportation of drug molecules across the cell membrane[1].
Many experiments[2, 3, 4],theoretical investigations[5, 6, 7, 8, 9, 10, 11],and numerical simulations[12, 13, 14, 15, 16, 17, 18, 19, 20, 21] have been carried out to understand the physical mechanism of the polymer through nanopores. Kong and Muthukumar[22] investigated the polymer translocation modified by the excluded volume effect among monomers,and showed that the excluded volume effect speeded up the translocation when the donor sphere was much smaller than the recipient sphere,the donor and recipient spheres were comparable in the size,and the excluded volume interaction induced a local minimum in the free energy landscape of translocation which could slow down the polymer translocation time tremendously. Yang and Neimark[23] and Park and Sung[24] investigated the effects of the adsorption potential on the translocation,and showed that the free energy was independent of the chain length at the critical adsorption potential for an ideal Gaussian chain. However,for a real chain,the critical point does not exist because of the excluded volume effect among the monomers. The free energy of a real chain is considerably larger than that of a Gaussian chain with the same chain length. Slonkina and Kolomeisky[25] studied the translocation process with the consideration of the effect of the nanopore dimension,and showed that the translocation velocity remained approximately constant when the chain length was much longer than the nanopore length while was inversely proportional to the nanopore length when the polymer length was shorter than the nanopore length. Mohan et al.[26] studied the effect of the charge distribution on the translocation of an inhomogeneously charged polymer through a nanopore.
Mohan et al.[27] and Wong and Muthukumar[28] investigated the polymer translocation of an ideal Gaussian chain through a cylindrical pore between two spherical compartments,illuminated the distribution of the translocation time and the free energy landscape of every stage,and showed that the diameters of two spherical compartments and the nanopore radius had significant effects on the average translocation time. However,in many biological processes,the polymer translocation happens in the electrolyte solution,and the charged ions in the electrolyte solution have obviously effects on the conformation free energy (the electrolyte effect).
Zhang et al.[29] found a phenomenon that the translocation time increased in the solution with high-valence salt,e.g.,MgCl2,which might perform as a moderator. It reveals that the property of the electrolytic solution may remarkably affect the translocation velocity of DNA molecules.
To explore the dynamic process of the polymer chain translocation through a nanopore,a novel theoretical model is developed based on the self-consistent field theory (SCFT) and the transport theory,where the electrolyte effect and the excluded volume effect are considered. The self-consistent field theory is used to discuss the diffusion process of the polymer,including the excluded volume effect and the external potential. The aqueous solution motion is described by the fluid mechanics equation. The distribution of the charged ions is derived by the particle transport equation. A theoretical model including the electrolyte effect is established by coupling the above equations.
2 Theoretical modelLet us assume that both donor and recipient are spheres,which are fully filled with the electrolyte solution. These two spheres are connected by a cylindrical nanopore with the axial length l0. The electrolyte solution is composed of the incompressible homogeneous Newtonian fluid and the charged ions. We only consider the electrolyte effect and the excluded volume effect in these two spheres because the size of the nanopore is small enough. As Fig. 1 shows,in the model,the radius of the nanopore is taken to be small enough for only a train of polymer segments so as to thread through,while the hairpin conformations are disallowed. The biomacromolecule is regarded as the freely jointed polymer chains consisting of N steps of Kuhn,each of which has the length of b. The number of the segments of the polymer chains is approximated to be a continuous variable,because N is tremendous. The absorbing potential between the nanopore and the polymer chain can be approximately described by the energy parameter ε.
 |
| Fig. 1 Schematic figure of translocating polymer chain |
Assume that the external electric potential difference between the two spheres is △V1,2. The external electric field intensity is
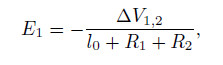
and the electric field intensity of the electric double layer field is E2. Then,the Navier-Stokes equations of the aqueous solution in the spheres can be expressed as follows:
where the electric potential of the electric double layer φ satisfies[30]
The boundary conditions for Eq. (1) are specified as follows:
The boundary conditions for Eq. (2) are specified as follows:
where the donor sphere R = R1,and the recipient sphere R = R2.
The ion density is
Equations (1) and (2) and the boundary conditions (3) and (4) are dispersed by use of the finite difference method,and then solved by the the successive over relaxation (SOR) numerical method.
2.2 Distribution equation of charged ions in spheresThe equilibrium distribution of the charged ions in the electrolyte will reach equilibrium from the non-equilibrium state under the external potential and the interaction between the ions. The interaction between the ions is described by use of the Coulomb potential. The evolution of the distribution function of the charged ions satisfies the Fokker-Planck equation expressed as follows[31]:
where
The first item on the right-side of Eq. (6) denotes the drift of the ions caused by Brown’s effect in the velocity space,while the second item denotes the diffusion of the ions caused by the Coulomb interaction.
The boundary conditions of Eq. (6) are
Assume that fi is approximately linear when the speed range is small enough. Equation (6) is dispersed by use of the finite difference method,and then solved by the Newton-SOR numerical method.
2.3 Diffusion equation including effects of electrolyte and excluded volumeThe polymer chain considered the excluded volume effect is simulated as the stochastic diffusion process under the electrolyte. Assume that the conformation of the polymer chain in the spheres is spherically symmetrical. Then,we can obtain a distribution function G(r,r1,s) by the SCFT theory[32],which means that the polymer chain probably has s segments in the spheres and the chain end resides,respectively,at r and r1. With the s segments in the spheres,the probability that one chain end resides at r and the other end resides at anywhere can be expressed by
The probability function F(r,s) obeys
The boundary condition of Eq. (13) is specified as follows:
The external potential of Eq. (13) can be given by
where ωρ(r) represents the excluded volume effect of the polymer chain. ω represents the excluded volume parameter between the chain segments,which is equivalent to the excluded volume of one segment. The potential function U(r) in the spheres includes the electrostatic potential field and the Coulomb potential between the ions and the polymer chain. Since the time for the ions reaching an equilibrium state (generally on the order in the range from 10−15 s to 10−12 s) is far less than the translocation time of the polymer chain (generally on the order of 10−4 s),the distribution function of the ions fi and the polymer chain F(r,s) can be considered to be independent of each other. Therefore,the equilibrium distribution of the ions feqi can be used to calculate the Coulomb potential between the ions and the polymer chain,which can be expressed by
The electrostatic potential field acting on the polymer chain at r in the donor sphere is given by
While in the recipient sphere,
When one end of the polymer chain is tethered at r0 and the other end is free,we can define the probability function as follows:
where
The probability function FT(r,s) also satisfies Eqs. (13) and (14). Equation (13) can be also solved by numerical iterations.
We assume a distribution ρ(0)(r),and obtain φ(0) through Eq. (15). F(0) can be solved by taking φ(0) into Eq. (13). ρ(1)(r) can be obtained through the integral equation (17). This iteration will continue until F(r,s) satisfies a certain accuracy.
3 Free energy of conformation and translocation time of polymer chain 3.1 Free energy of conformation in process of polymer chain through nanoporeDuring the translocation of the polymer chain through nanopores,the free energy of the conformation can be calculated by the confinement probability. The translocation from the donor sphere to the recipient sphere can be divided into three stages:
(i) One end of the polymer chain finds the entrance of the nanopore (see Figs. 2(a) and 2(b)).
 |
| Fig. 2 Polymer chain configurations during translocation from donor sphere to recipient sphere through cylindrical pore |
(ii) The polymer chain translocates through the nanopores (see Figs. 2(b) and 2(c)).
(iii) The polymer chain gradually translocates into the recipient sphere (see Figs. 2(c)-2(e)).
The free energy of the conformation of the polymer chain at each stage can be given as follows:
(Ⅰ) When the polymer chain resides in the donor sphere,the free energy of the conformation of the polymer chain can be expressed by
(Ⅱ) When one end of the polymer chain is tethered at the entrance of the nanopores,and the rest part resides in the donor sphere,the free energy of the conformation of the polymer chain can be calculated by
(Ⅲ) Assume that the average interaction potential between each segment and nanopore can be expressed as ε,which is positive when the interaction potential is absorbing while negative when the interaction potential is mutually exclusive. When s segments reside in the nanopore and (N − s) segments reside in the donor sphere,the free energy of the conformation of the polymer chain can be calculated by
(Ⅳ) When M segments reside in the nanopore,s segments reside in the recipient sphere,and (N −M − s) segments reside in the donor sphere,the free energy of the conformation of the polymer chain can be calculated by
(Ⅴ) When (N − s) segments reside in the nanopore,and s segments reside in the recipient sphere,the free energy of the conformation of the polymer chain can be calculated by
3.2 Translocation time
The duration from the polymer chain starting from the nanopore to the polymer chain totally getting into a recipient sphere can be described as the average translocation time <τ>,which can be calculated by the mean first-passage time. Following Eq. (36) yields the mean first-passage time as follows:
where the reflective boundary condition is used at s = s0,and the absorbing boundary condition is used at s = s1.
The solution of Eq. (36) can be written as follows:
The translocation time <τ> is consisted of three stages. The initial status and the termination status of the first stage are shown in Figs. 2(b) and 2(c),respectively. The initial status and the termination status of the second stage are shown in Figs. 2(d) and 2(e),respectively. The translocation time of each stage can be expressed by
which can be solved by the numerical integral equation (37).
The expression of F(b→c) can be given by Eq. (26). The expression of F(c→d) can be given by Eq. (30). The expression of F(d→e) can be given by Eq. (34).
4 Results and discussionThe equilibrium distribution of Mg2+ ions along the radial direction in the donor sphere is shown in Fig. 3(a),and the equilibrium distribution of Mg2+ ions as a function of the velocity in the donor sphere is shown in Fig. 3(b). The results show that the ions are mainly distributed in the center of the sphere and few resides at the wall position in Fig. 3(a). Moreover,the equilibrium distribution of the ions is approximately a Maxwell distribution in the ion velocity space (see Fig. 3(b)).
 |
| Fig. 3 Equilibrium distribution of Mg2+ ions in donor sphere, where N = 120, electrolyte is MgCl2, electrolyte concentration is 1mol, and ω = 0.5 |
The results show that the conformation free energy at both cases varies monotonically with the chain length N and the existence of the excluded volume effect leads to an increase in the free energy of the polymer chain at the same chain length in Fig. 4. As shown in Figs. 4(a) and 4(b),the free energy of the tethered polymer chain is smaller than that of the free polymer chain. The conformation of the polymer chain is limited,since one end of the polymer chain is tethered at the entrance of the nanopore. Therefore,the entropy decreases at the same chain length,and excludes the volume effect parameter. The result predicted by this model agrees with that in Ref. [24].
 |
| Fig. 4 Free energy of polymer chain in donor sphere as function of chain length N at stages of Figs. 2(a) and 2(b), where electrolyte is MgCl2, electrolyte concentration is 1mol, and R1 = 30b |
Figure 5 shows the conformation free energy with the polymer chain diffusion in the nonelectrolyte solution and the electrolyte MgCl2 at the stages of Figs. 2(a) and 2(b). It shows that when the polymer is in the electrolyte solution,the conformation free energy increases. The reason is that the Coulomb electrostatic potential between the charged ions and the polymer chain segments makes the conformations of the polymer chain become more disorderly. Therefore,the conformation free energy in the electrolyte is extended.
 |
| Fig. 5 Comparison of free energy change of polymer chain with polymer chain diffusion in nonelectrolyte solution and MgCl2 at stages of Figs. 2(a) and 2(b), where electrolyte concentration is 1mol, and ω = 0.5 |
Figure 6 plots the free energy 
as functions of the translocation coordinate s with the donor sphere of the nonelectrolyte solution and the donor sphere filled with the electrolyte MgCl2. The results show that the free energy increases with an increase in the translocation coordinate s. When the translocation coordinate s increases and the number of the segments inside the donor sphere decreases,the absorbing potential between the nanopore and the polymer chain increases gradually. Meanwhile,the conformations of the polymer chain in the donor sphere decrease with a decrease in the segment number inside the donor sphere. Therefore,the entropy barrier declines and the free energy increases. Moreover,the conformation free energy in the electrolyte solution is more extended than that in the nonelectrolyte solution at the same value of s. The reason is that the coulomb electrostatic interaction between the charged ions and the polymer chain makes the conformations of the polymer chain become more disordered. Therefore,the entropy barrier of the conformations will be increased and the free energy will be reduced.
 |
|
Fig. 6 Free energy as function of s with donor sphere filled with nonelectrolyte solution and donor sphere filled with electrolyte MgCl2, where s denotes number of segments inside nanopore, N = 120, electrolyte concentration is lmol, and ω = 0.5 |
Figure 7 shows that the free energy 
changes non-monotonically with an increase in the translocation coordinate s. The free energy gradually increases to reach a maximum sc (sc ≈ 35),and then gradually declines with the increase in the translocation coordinate s. When the number of the segments inside the donor sphere decreases with an increase in the translocation coordinate s,the conformation states in the donor sphere decrease,and the entropy barrier of the polymer chain in the donor sphere declines. Similarly,the entropy barrier of the polymer chain in the recipient sphere increases. When s is smaller than sc,the reduction of the conformation entropy in the donor sphere is greater than the augment of the conformation entropy in the recipient sphere,and the total conformation entropy will be reduced. Therefore,the free energy increases gradually,and reaches a maximum. On the contrary,when s is greater than sc,the free energy falls down,and the conformation free energy in the donor sphere filled with the electrolyte is less than that in the nonelectrolyte solution at the same value of s. The reason is the same as that of Fig. 6.
 |
|
Fig. 7 Free energy as function of s with donor sphere filled with nonelectrolyte solution and donor sphere filled with electrolyte MgCl2, where s denotes number of segments inside nanopore, N = 120, electrolyte concentration is lmol, and ω = 0.5 |
Figure 8 shows that the free energy 
gradually declines with the increase in the translocation coordinate s. When the number of the conformation states of the polymer chain increases,the number of the segments inside the recipient sphere and the conformation entropy of the polymer chain increase,while the attraction effect of the nanopore on the polymer chain is weakened. Therefore,the free energy decreases. The conformation free energy in the recipient sphere filled with electrolyte is less than that in the volume at the same value of s.
 |
|
Fig. 8 Free energy as function of s with donor sphere filled with nonelectrolyte solution and donor sphere filled with electrolyte MgCl2, where s denotes number of segments inside nanopore, N = 120, electrolyte concentration is lmol, and ω = 0.5 |
Figure 9(a) shows that when the number of the segments inside the nanopore increases,the whole chain conformation number will be reduced due to the confine by the nanopore,and the entropy S(b→c) will decrease monotonously at the same time. Figure 9(b) shows that the entropy S(c→d) exits a minimum value in the process through the nanopore. When a small number of segments are in the recipient sphere,the reduction of the conformation in the donor sphere is greater than the increment of the conformation in the recipient sphere so that the conformation entropy decreases. When a large number of segments are in the recipient sphere,contrarily,the whole chain will be more disordered,leading to the decrease in the conformation entropy. Figure 9(c) shows that the entropy S(d→e) increases monotonously when more chain segments translocate into the recipient sphere. When less and less segments stay in the nanopore,the absorbing potential between the nanopore and the polymer chain will get weakened. Meanwhile,more and more segments translocate into the recipient sphere,the whole chains will be more disordered,and the entropy S(d→e) will increase. The electrolyte effect will make the conformation of the polymer chain have a tendency to be disordered during each stage of the translocation. Therefore,the entropy considering the effect of the electrolyte is greater than that not considering the effect of the electrolyte at the same value of s.
 |
| Fig. 9 Curves of entropy barrier as function of s, where s denotes number of segments inside nanopore in Fig. 9(a) or recipient sphere in Figs. 9(b) and 9(c), N = 210, electrolyte is MgCl2, electrolyte concentration is 1mol, and ω = 0.5 |
Figure 10 shows the distribution of the segment density considering the electrolyte effect at the stage of Fig. 2(a). It reveals that the maximum value exits at the point r*= 0.4 for the distribution of the segment density,regardless of the chain length. The excluded volume effect is proportional to the segment density. Therefore,the excluded volume effect is the strongest around the range of r* = 0.4 and the weakest near the center or boundary of the sphere. Figure 10 also shows that the excluded volume effect will increase when the chain length is longer,while the polymer length has little impact on the excluded volume effect at the boundary or center of the sphere.
 |
| Fig. 10 Segment density of polymer chain as function of radius direction in donor sphere, where electrolyte is MgCl2, electrolyte concentration is lmol, and ω = 0.5 |
Figures 11(a) and 11(b) show that the average translocation time will extend when the surface charge of a polymer chain increases. When the surface charge distribution remains the same,the electrolyte effect will result in an increase in the average translocation time. Furthermore,the higher the valency number of the electrolyte is,the longer the average translocation time is. This is because that the Coulomb electrostatic potential between the polymer chain and the charged ions in the electrolyte will result in the resistance effect,and the resistance effect will be stronger when the valency number of the electrolyte increases.
 |
| Fig. 11 Average translocation time as function of surface charge of polymer chain |
Figures 12(a) and 12(b) show that the translocation time <τ1> (from the stage of Fig. 2(b) to the stage of Fig. 2(c)) and the translocation time <τ2> + <τ3> (from the stage of Fig. 2(c) to the stage of Fig. 2(e)) increase monotonously with the increase in the chain length N,and the translocation time that the polymer chain translocating through the nanopore is far less than that fully filled with the recipient sphere at the same value of N. Moreover,the average translocation time in the electrolyte MgCl2 is longer than that in the electrolyte KCl at the same value of N,because the polymer chain will be more disordered for high valence electrolyte and the conformation entropy will be larger. Consequently,high valence electrolyte can extend the translocation time. The result in Fig. 12(c) agrees with the experiment data shown in Ref. [31].
 |
| Fig. 12 Translocation time as function of chain length N at each stage for different electrolytes and translocation time of experimental data contrast to simulation data, where electrolyte concentration is 1mol, ω = 0.5, and N = 270 |
A novel theoretical model is developed based on the SCFT theory and the transport theory to describe the process of the polymer chain translocating through nanopores. The results show that the proposed model can couple the electrolyte effect,the surface charge effect,and the excluded volume effect,and a minimum conformation entropy exists in the process of getting into the recipient sphere in the case considering the excluded volume effect. The electrolyte effect makes the polymer chain become more disordered at each stage,and the conformation entropy is larger than that without electrolyte. When the polymer length remains the same,the electrolyte effect will result in an increase in the average translocation time. Furthermore,the average translocation time will extend when the valency number of the electrolyte increases. The translocation time will be much longer in higher valence solutions. For long chains,consider the excluded volume effect. Then,<τ1> and <τ2>+<τ3> increase with an increase in the polymer length N,and the time <τ1> used to fully fill the nanopore (from the stage of Fig. 2(b) to the stage of Fig. 2(c)) is much shorter than the time <τ2> + <τ3> used to fully fill the recipient sphere (from the stage of Fig. 2(c) to the stage of Fig. 2(e)). During the translocation,with an increase in the surface charge of a polymer chain,the resistance effect generated by the Coulomb electrostatic potential will increase,resulting in an increase in the average translocation time.
| [1] | Branton, D. and Deamer, D. W. Membrane Structure, Springer-Verlag, Berlin, 1-70 (1972) |
| [2] | Akeson, M., Branton, D., Kasianowicz, J. J., Brandin, E., and Deamer, D. W. Microsecond time-scale discrimination among polycytidylic acid, polyadenylic acid, and polyuridylic acid as homopolymers or as segments within single RNA molecules. Biophysical Journal, 77, 3227-3233 (1999) |
| [3] | Kasianowicz, J. J., Brandin, E., Branton, D., and Deamer, D. W. Characterization of individual polynucleotide molecules using a membrane channel. Proceedings of the National Academy of Sciences, 93, 13770-13773 (1996) |
| [4] | Henrickson, S. E., Misakian, M., Robertson, B., and Kasianowicz, J. J. Driven DNA transport into an asymmetric nanometer-scale pore. Physical Review Letters, 85, 3057 (2000) |
| [5] | Sung, W. and Park, P. J. Polymer translocation through a pore in a membrane. Physical Review Letters, 77, 783 (1996) |
| [6] | Muthukumar, M. Translocation of a confined polymer through a hole. Physical Review Letters, 86, 3188 (2001) |
| [7] | Chuang, J., Kantor, Y., and Kardar, M. Anomalous dynamics of translocation. Physical Review E, 65, 011802 (2001) |
| [8] | Wong, C. T. A. and Muthukumar, M. Polymer translocation through a cylindrical channel. The Journal of Chemical Physics, 128, 154903 (2008) |
| [9] | Wong, C. T. A. and Muthukumar, M. Scaling theory of polymer translocation into confined regions. Biophysical Journal, 95, 3619-3627 (2008) |
| [10] | Wolterink, J. K., Barkema, G. T., and Panja, D. Passage times for unbiased polymer translocation through a narrow pore. Physical Review Letters, 96, 208301 (2006) |
| [11] | Lubensky, D. K. and Nelson, D. R. Driven polymer translocation through a narrow pore. Biophysical Journal, 77, 1824-1838 (1999) |
| [12] | Milchev, A., Binder, K., and Bhattacharya, A. Polymer translocation through a nanopore in-duced by adsorption: Monte Carlo simulation of a coarse-grained model. The Journal of Chemical Physics, 121, 6042-6051 (2004) |
| [13] | Matsuyama, A., Yano, M., and Matsuda, A. Packaging-ejection phase transitions of a polymer chain: theory and Monte Carlo simulation. The Journal of Chemical Physics, 131, 105104 (2009) |
| [14] | Matsuyama, A. Phase transitions of a polymer escaping from a pore. Journal of Physics: Condensed Matter, 17, S2847 (2005) |
| [15] | Gauthier, M. G. and Slater, G. W. A Monte Carlo algorithm to study polymer translocation through nanopores, I: theory and numerical approach. The Journal of Chemical Physics, 128, 065103 (2008) |
| [16] | Fyta, M., Melchionna, S., Succi, S., and Kaxiras, E. Hydrodynamic correlations in the transloca-tion of a biopolymer through a nanopore: theory and multiscale simulations. Physical Review E, 78, 036704 (2008) |
| [17] | Fyta, M., Melchionna, S., Succi, S., and Kaxiras, E. Hydrodynamic correlations in the transloca-tion of a biopolymer through a nanopore: theory and multiscale simulations. Physical Review E, 78, 036704 (2008) |
| [18] | Bhattacharya, A., Morrison, W. H., Luo, K., Ala-Nissila, T., Ying, S. C., Milchev, A., and Binder, K. Scaling exponents of forced polymer translocation through a nanopore. The European Physical Journal E: Soft Matter and Biological Physics, 29, 423-429 (2009) |
| [19] | Luo, K., Metzler, R., Ala-Nissila, T., and Ying, S. C. Polymer translocation out of confined environments. Physical Review E, 80, 021907 (2009) |
| [20] | Yu, W. C. and Luo, K. F. Chaperone-assisted translocation of a polymer through a nanopore. Journal of the American Chemical Society, 133, 13565-13570 (2011) |
| [21] | Alapati, S., Fernandes, D. V., and Suh, Y. K. Numerical and theoretical study on the mechanism of biopolymer translocation process through a nanopore. The Journal of Chemical Physics, 135, 055103 (2011) |
| [22] | Kong, C. Y. and Muthukumar, M. Polymer translocation through a nanopore, II: excluded volume effect. The Journal of Chemical Physics, 120, 3460 (2004) |
| [23] | Yang, S. and Neimark, A. V. Adsorption-driven translocation of polymer chain into nanopores. The Journal of Chemical Physics, 136, 214901 (2012) |
| [24] | Park, P. J. and Sung, W. Polymer translocation induced by adsorption. The Journal of Chemical Physics, 108, 15-23 (1998) |
| [25] | Slonkina, E. and Kolomeisky, A. B. Polymer translocation through a long nanopore. The Journal of Chemical Physics, 118, 7112-7118 (2003) |
| [26] | Mohan, A., Kolomeisky, A. B., and Pasquali, M. Effect of charge distribution on the translocation of an inhomogeneously charged polymer through a nanopore. The Journal of Chemical Physics, 128, 125104 (2008) |
| [27] | Mohan, A., Kolomeisky, A. B., and Pasquali, M. Polymer translocation through pores with com-plex geometries. The Journal of Chemical Physics, 133, 024902 (2010) |
| [28] | Wong, C. T. A. and Muthukumar, M. Polymer translocation through a cylindrical channel. The Journal of Chemical Physics, 128, 154903 (2008) |
| [29] | Zhang, Y., Liu, L., Sha, J. J., Ni, Z. H., Yi, H., and Chen, Y. F. Nanopore detection of DNA molecules in magnesium chloride solutions. Nanoscale Research Letters, 8, 1-8 (2013) |
| [30] | Gardiner, C. W. Handbook of Stochastic Methods: for Physics, Chemistry and the Natural Sciences, Springer-Verlag, Berlin (1983) |
| [31] | Lin, X. H., Zhang, C. B., Gu, J., Jiang, S. Y., and Yang, J. K. Poisson-Fokker-Planck model for biomolecules translocation through nanopore driven by electroosmotic flow. Science China-Physics, Mechanics & Astronomy, 57, 2104-2113 (2014) |
| [32] | Fredrickson, G. H. The Equilibrium Theory of Inhomogeneous Polymers, Clarendon Press, Oxford, 34-97 (2006) |