Shanghai University
Article Information
- M. AREFI, R. KARROUBI, M. IRANI-RAHAGHI. 2016.
- Free vibration analysis of functionally graded laminated sandwich cylindrical shells integrated with piezoelectric layer
- Appl. Math. Mech. -Engl. Ed., 37(7): 821-834
- http://dx.doi.org/10.1007/s10483-016-2098-9
Article History
- Received 2015-12-10;
- in final form 2016-03-22
Vibration analysis of structures for calculation of natural frequencies and corresponding mode shapes was frequently performed by researchers. These analyses are necessary for structures subjected to harmonic loading to avoid resonance. The natural frequencies of the system depend on the material properties as well as boundary conditions. Stiffness, density, and distribution of them can significantly change the vibration behavior of structures. To control the vibration characteristics of the structures and avoiding the resonance, functionally graded materials (FGMs) may be suggested. These materials with variable directional properties can offer the best combination of materials and tend to optimized distribution of material properties.
Furthermore, to control the vibration behaviors of the structures, using the piezoelectric materials such as sensor or actuator is suggested. Piezoelectric materials as thin layers can be attached to main structures to evaluate and control the vibration characteristics of the structures. This paper investigates vibration analysis of a functionally graded cylindrical shell integrated with functionally graded piezoelectric (FGP) layers based on a three-dimensional analysis. The comprehensive literature review can justify necessity of this study.
Shu[1] used the generalized differential quadrature (GDQ) to study the free vibration of isotropic conical shells. The fundamental frequency parameters for four sets of boundary conditions and various semi vertex angles were shown in the paper. The accuracy and efficiency of the GDQ method were examined by comparing the results with previously published results, and good agreement was observed. Lam and Qian[2] developed an analytical solution for the vibrations of thick symmetric angle-ply laminated composite cylindrical shells using the firstorder shear deformation theory (FSDT). The influence of the lamination angle and the number of lamination layers was considered on the frequency of system. Chen et al.[3] investigated the three-dimensional free vibration analysis of a functionally graded thick orthotropic piezoelectric hollow cylinder filled with fluid. The effect of internal fluid was considered as a relation between the fluid pressure and the radial displacement at the interface. The frequency equations were derived for some boundary conditions, and the effects of various parameters on the natural frequencies were investigated. Patel et al.[4] studied free vibration analysis of functionally graded elliptical cylindrical shells using the finite element formulated based on the higher-order theory. The finite element used in the study was based on the field-consistency approach and free from shear and membrane locking problems. The influence of different parameters on the free vibration frequencies and mode shapes was investigated at the end.
Wang and Redekop[5] developed free vibration characteristics of an orthotropic thin shell of revolution. They used the Sanders-Budiansky shell theory and the differential quadrature method (DQM). Numerical examples for frequencies and mode shapes were given. The obtained results of the DQM were compared with the results obtained using the finite element method. Kurpa et al.[6] studied vibration of composite laminated shallow shells resting on an arbitrary planform using the FSDT. The proposed method involves the use of the R-functions theory and variation methods. They studied the effects of various parameters such as the planform geometry, the lamination scheme, the curvatures, and boundary conditions on the dynamical behavior of the shell.
Tornabene et al.[7] developed a two-dimensional GDQ solution for free vibrations of FGM laminated doubly curved shells and panels of revolution based on the FSDT. In order to include the effect of the initial curvature, a generalization of the Reissner-Mindlin theory, proposed by Toorani and Lakis, was adopted. To include the effect of the initial curvature, a generalization of the Reissner-Mindlin theory was adopted. Comparisons between the Reissner-Mindlin and Toorani-Lakis theories were presented. Furthermore, the GDQ results were compared with those obtained by commercial programs. Neves et al.[8] investigated free vibration analysis of functionally graded shells based on the higher-order shear deformation theory and the radial basis functions collocation. The equations of motion and the boundary conditions were obtained using Carrera’s unified formulation resting upon the principle of virtual work, and further interpolated by collocation with radial basis functions. Numerical results include spherical as well as cylindrical shell panels with different boundary conditions.
Sheng and Wang[9] studied nonlinear vibration control of functionally graded laminated cylindrical shells. They presented a new simplifying model of smart functionally graded laminated cylindrical shells with thin piezoelectric layers based on Hamilton’s principle and nonlinear von Karman strain-displacement and constant-gain negative velocity feedback approach. They derived equations of motion as the coupled nonlinear partial differential equations. The derived equations were discretized based on multi-term Galerkin’s method. The Runge-Kutta method was used for numerical analysis of the problem. Kumar et al.[10] studied free vibration response of sandwich shells based on the zigzag theory using an efficient two-dimensional finite element model. The finite element formulation was used for analysis of the problem. The numerical studies indicated that the present two-dimensional finite element model was more accurate than the existing finite element models based on first- and higher-order theories for predicting results.
Ebrahimi and Najafizadeh[11] developed free vibration analysis of two-dimensional functionally graded cylindrical shells based on Love’s first approximation classical shell theory. The spatial derivatives of the equations of motion and boundary conditions were discretized by the methods of GDQ and generalized integral quadrature (GIQ). In order to describe the material properties, two kinds of micromechanics models, i.e., Voigt and Mori-Tanaka models, were used. The results were validated by comparing with the previously published results.
Duc et al.[12] studied nonlinear vibration of shear deformable functionally graded piezoelectric material (FGPM) double curved shallow shells under different loads. Material properties of FGM shells were assumed to be temperature dependent and graded in the thickness direction according to a simple power-law distribution in terms of the volume fractions of the constituents. The governing equations were established based on Reddy’s higher-order shear deformation theory that includes thermo-piezoelectric effects and were solved by the stress function, the Galerkin method, and the fourth-order Runge-Kutta method. In numerical results, the effects of different parameters on the nonlinear vibration were discussed.
Wali et al.[13] developed free vibration analysis of FGM shell structures using a threedimensional- shell model based on a discrete double directors shell element. Transverse shear strains on top and bottom faces were considered in a discrete form. The mechanical properties of the shell structure were assumed to vary continuously in the thickness direction according to the general four-parameter power-law distribution in terms of the volume fractions of the constituents. The equations of motion for the system were derived using the principle of virtual work.
Assaee and Hasani[14] studied the forced vibration behavior of thin walled composite circular cylindrical shells using the spline finite strip method. They used the classical bending theory of shells and Sanders-Koiter’s strain-displacement relation. In order to validate the results, a comparison with the finite element results was performed. They extracted the natural frequencies using the fast Fourier transform from the time history response.
In this work, a free vibration three-dimensional analysis of laminated sandwich shell is investigated. The FSDT is used for description of displacement components. Non-homogeneities are considered for both core and integrated piezoelectric layers. Hamilton's principle is used to derive partial differential equations of motion. The numerical results of natural frequency analysis are presented for simply supported cylindrical shell in terms of different parameters of the system. The effect of geometric parameters such as thickness and length and the effect of material properties gradation of both FGM and FGPM sections can be studied on the responses of the system in detail.
2 Theory and formulationThe fundamental relations of the functionally graded cylindrical shell integrated with FGP layers are presented in this section. The schematic figure of the problem is plotted in Fig. 1. The required notation and coordinates are presented in the mentioned figure. The inner and outer layers are considered as FGPMs that are named as sensor and actuator, respectively. The orthogonal curvilinear coordinates (x, θ, z) are assumed to be at the middle surface of the core. The required terms such as the thicknesses of core, sensor, and actuator are presented as h, hs, and ha, respectively.

|
| Fig. 1 Schematic of cylindrical shell |
According to the FSDT, the displacement field is considered as[2, 15, 16]
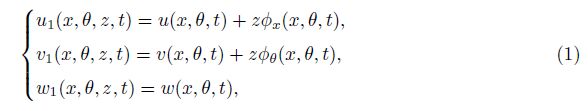
in which (u, v, w) are the mid-surface displacements along the x-, θ-, and z-directions, respectively, and φx and φθ represent the rotations of the normal vector of the mid-surface along the x- and θ-axes, respectively.
The normal and transverse shear strains considering the von Karman terms are expressed as[2]
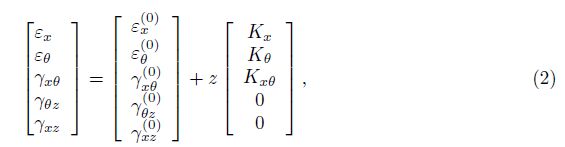
where the strains of mid-surface and curvature defined in Eq. (2) are expressed as[2, 17]
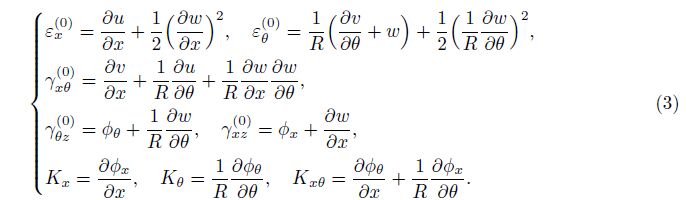
The FGM and FGPM layers properties are assumed to change along the thickness direction z as follows[18, 19]:
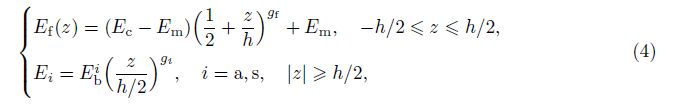
in which f, a, and s represent the functionally graded core, actuator, and sensor, respectively. The first equation demonstrates the distribution of material properties for FGM shell, and the second equation is used for FGPM properties, where subscripts m and c refer to the metal and ceramic constituents, respectively. Ef includes the density and Young’s modulus of the functionally graded core, and Eb includes the density, Young’s modulus, and the stiffness matrix elements of the actuator and sensor sections. Poisson’s ratio of FGMs is assumed to remain constant because of small change.
After defining the material properties and strain-displacement relation, the stress-strain relations for FGM section and stress-strain equations considering the electric field for FGPM sections are presented as follows[9, 20]:
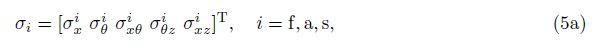
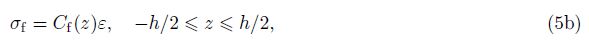
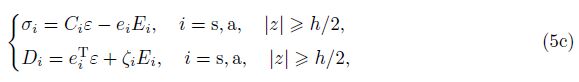
in which C is the stiffness matrix. D and E demonstrate the electrical displacement and the electrical field, respectively. The matrices of material properties are expressed as

where eij and ζij represent the effective piezoelectric constant and the effective permittivity constant, respectively.
The electrical field in piezoelectric materials is obtained by the gradient of electric potential as follows[16, 21]:

in which φa and φs are electrical potentials of actuator and sensor sections, respectively. To consider an applied voltage in piezoelectric layers, the electrical potential function for the actuator section is introduced as[21]
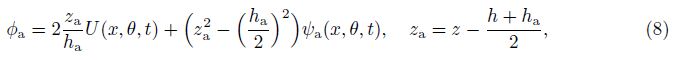
in which U(x, θ, t) is the applied electrical potential, and ψa indicates the distribution of the electric potential along the planar coordinate of the actuator integrated layer.
The electric potential distribution for the sensor section is considered as
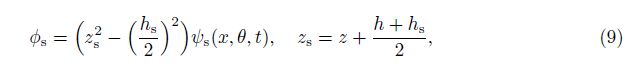
in which, similar to the electric potential of the actuator section, ψs indicates the distribution of electric potential along the planar coordinate of sensor integrated layers.
In order to derive the equations of motion, Hamilton’s principle is used[11],
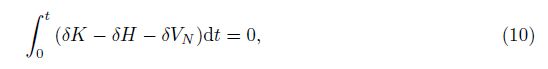
in which K, H, and VN are the total kinetic energy, the total potential energy of the system containing the core FGM layer and both two piezoelectric layers, and the external axial loading work, respectively[22], and
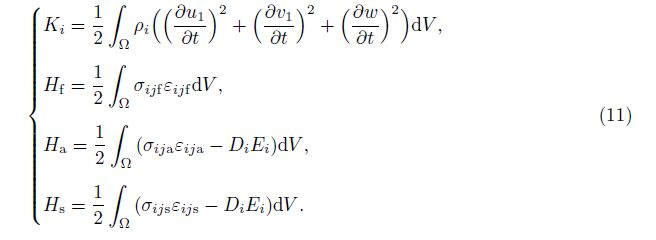
By substitution of the required terms of stress, strain, electric displacement, electric potential, and kinetic energy, the final governing equations of motion are derived in the familiar forms as

in which Ii and kij are components of mass and stiffness coefficients in Appendix A.
The governing equations of system can be obtained for a cylindrical shell with simply-supported boundary conditions using the Navier solution as follows[9]:
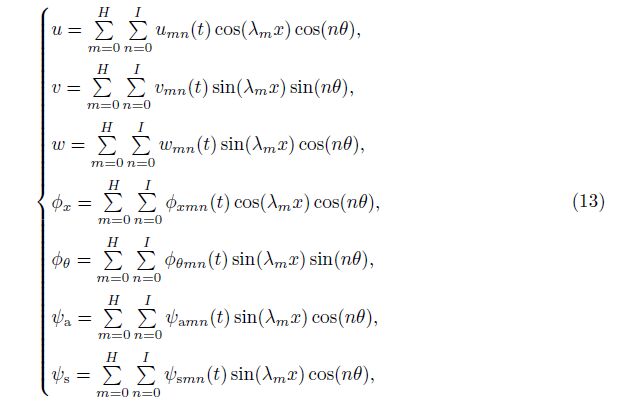
in which  , and m and n represent the numbers of axial and circumferential half-waves, respectively. By substituting the solution as presented in Eq. (13) into the equations of motion, the coupled system of partial differential equations converts to ordinary differential equations as follows:
, and m and n represent the numbers of axial and circumferential half-waves, respectively. By substituting the solution as presented in Eq. (13) into the equations of motion, the coupled system of partial differential equations converts to ordinary differential equations as follows:

in which Tij can be calculated by substituting Eq. (13) in kij that are described in Appendix A.
The last two equations of Eq. (14) are algebraic equations that can be easily solved as follows:
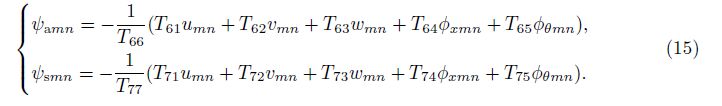
Substitution of the obtained solutions for two electric potential functions in the remained five functions leads to the final governing equations of the system. The natural frequencies of the system can be obtained by the defined matrices M and K in Eq. (15) as follows:
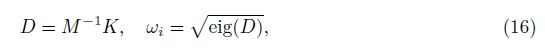
where eig(D) denotes the eigenvalues of D.
3 Results and discussionBy considering a specified material for FGM and FGPM sections, the numerical results can be evaluated in terms of different parameters of the system.
Table 1, Table 2, and Table 3 show geometric and material properties of the cylindrical shell. Aluminum (Al) at the bottom and alumina (Al2O3) at the top constitute the material properties of functionally graded core. The material properties change continuously and gradually along the thickness in terms of volume fraction of constituent materials[23]. Both sensor and actuator layers are made of PZT-4[16, 24, 25, 26].
After definition of material properties, the numerical results are depicted in terms of different parameters of cylindrical shell. Figure 2 is the distribution of natural frequencies of the cylinder in terms of non-homogeneous index (gf ) of functionally graded core for different values of non-homogeneous index of FGP layers (gp). It can be concluded that by increasing the nonhomogeneous index of core, the natural frequencies of the cylinder decrease. This decrease is due to high order increase of the cylinder mass rather than increase of the stiffness of cylinder. Furthermore, it can be observed that by increasing the non-homogeneous index of piezoelectric layers, the natural frequencies of the cylinder increase considerably. This increase is due to the increase of the bending stiffness of the cylinder caused by increasing the stiffness of integrated layers.

|
| Fig. 2 First natural frequencies of cylindrical shell in terms of different values of non-homogeneous index of core (gf ) and integrated layers (gp) |
The distributions of second and third natural frequencies of the cylindrical shell are presented in Figs. 3 and 4, respectively. An investigation on the presented results of high order natural frequencies of the cylinder indicates that by increasing the non-homogeneous index of functionally graded core (gf ), the natural frequencies decrease continuously due to the increase of the mass of cylinder rather than the increase of the stiffness of cylinder. The same discussion for the first natural frequency can be presented for the second and third natural frequencies of the system when the non-homogeneous indexes of functionally graded core and integrated layers change.

|
| Fig. 3 Second natural frequencies of system in terms of different values of nonhomogeneous index of core (gf) and integrated layers (gp) |

|
| Fig. 4 Third natural frequencies of system in terms of different values of nonhomogeneous index of core (gf) and integrated layers (gp) |
The effects of the core thickness and the integrated layers on the vibrational behavior of sandwich cylinder are considered. Figure 5 is the distribution of the first natural frequencies of the cylinder in terms of the ratio of core thickness to piezoelectric layer thickness hf/hp for different values of non-homogeneous index of piezoelectric layers (gp). The total thickness is assumed to be constant in order to investigate the importance of the core thickness in comparison of the piezoelectric thickness.

|
| Fig. 5 Distribution of first natural frequencies of cylinder in terms of ratio of core thickness to piezoelectric layer thickness hf/hp for different values of non-homogeneous index of piezoelectric layers (gp) |
It can be concluded that by increasing the assumed thickness ratio hf/hp, the first natural frequency of the cylinder increases. This increase is due to the increase of the bending stiffness of cylinder by increasing the thickness of the cylinder.
The effect of the cylinder length as another important parameter on the natural frequency is investigated. Figure 6 is the distribution of the first natural frequencies of the sandwich cylinder in terms of the length of the cylinder. A decreasing manner is observed for natural frequencies, when the length of the cylinder is increased. Increasing the length of the cylinder results in the increase of flexibility and yields lower frequencies.

|
| Fig. 6 Distribution of first natural frequencies of sandwich cylinder in terms of length of cylinder (L) |
The effect of the ratio of core thickness to cylinder length (hf/L) is considered on the responses of the cylinder in Fig. 7.

|
| Fig. 7 Distribution of first natural frequencies of sandwich cylinder in terms of ratio hf/L |
Figure 7 shows the distribution of the first natural frequencies of the sandwich cylinder in terms of ratio hf/L for different values of non-homogeneous index of piezoelectric layers. The obtained results in this figure indicate that by increasing the ratio hf/L, the natural frequencies of the cylinder increase considerably.
4 ConclusionsThe three-dimensional vibration analysis of a sandwich cylindrical shell containing a functionally graded core and two FGP layers as sensor and actuator is investigated. The FSDT is used for description of displacement field. Geometric nonlinearity is considered on the straindisplacement relations based on the von Karman relations. Non-homogeneity is considered for both core and integrated layers using the power law distribution. Using Hamilton’s principle and evaluation of strain and kinetic energies of the cylinder, the equations of motion are derived. Some important conclusions of this research are expressed.
(i) Investigation on the non-homogeneous index of functionally graded core indicates that by increasing this index, all natural frequencies (first, second, and third natural frequencies) of the system decrease. The reason is due to the increase of the mass of cylinder rather than the increase of the bending stiffness of cylinder. Unlike the effect of non-homogeneous index of functionally graded core, increasing the non-homogeneous index of FGP layers tends to increase the natural frequencies of the system.
(ii) The geometric parameters of the cylinder have important effect on the vibration behavior of the cylinder. Increasing the ratio hf/L tends to increase the natural frequencies of the cylinder. A cylinder with greater hf/L reflects greater bending stiffness that causes the increase of natural frequencies. Increasing the length of the cylinder causes the decrease of the natural frequencies of the cylinder due to the increase of the flexibility and consequently causes the decrease of the stiffness of the cylinder.
Appendix A



| [1] | Shu, C. An efficient approach for free vibration analysis of conical shells. International Journal of Mechanical Science, 38(8/9), 935-949(1995) |
| [2] | Lam, K. Y. and Qian, W. Free vibration of symmetric angle-ply thick laminated composite cylindrical shells. Composites:Part B, Engineering, 31, 345-354(2000) |
| [3] | Chen, W. Q., Bian, Z. G., Lv, C. F., and Ding, H. J. 3D free vibration analysis of a functionally graded piezoelectric hollow cylinder filled with compressible fluid. International Journal of Solids and Structures, 41, 947-964(2004) |
| [4] | Patel, B. P., Gupta, S. S., Loknath, M. S., and Kadu, C. P. Free vibration analysis of functionally graded elliptical cylindrical shells using higher-order theory. Composite Structures, 69, 259-270(2005) |
| [5] | Wang, X. H. and Redekop, D. Natural frequencies and mode shapes of an orthotropic thin shell of revolution. Thin-Walled Structures, 43, 735-750(2005) |
| [6] | Kurpa, L., Shmatko, T., and Timchenko, G. Free vibration analysis of laminated shallow shells with complex shape using the R-functions method. Composite Structures, 93, 225-233(2010) |
| [7] | Tornabene, F., Liverani, A., and Caligiana, G. FGM and laminated doubly curved shells and panels of revolution with a free-form meridian:a 2-D GDQ solution for free vibrations. International Journal of Mechanical Sciences, 53, 446-470(2011) |
| [8] | Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Cinefra, M, Roque, C. M. C., Jorge, R. M. N., and Soares, C. M. M. Free vibration analysis of functionally graded shells by a higher-order shear deformation theory and radial basis functions collocation, accounting for through-the-thickness deformations. European Journal of Mechanics A/Solids, 37, 24-34(2013) |
| [9] | Sheng, G. G. and Wang, X. Nonlinear vibration control of functionally graded laminated cylindrical shells. Composites:Part B, Engineering, 52, 1-10(2013) |
| [10] | Kumar, A., Chakrabarti, A., and Bhargava, P. Vibration of laminated composites and sandwich shells based on higher order zigzag theory. Engineering Structures, 56, 880-888(2013) |
| [11] | Ebrahimi, M. J. and Najafizadeh, M. M. Free vibration analysis of two-dimensional functionally graded cylindrical shells. Applied Mathematical Modelling, 38, 308-324(2014) |
| [12] | Duc, N. D., Quan, T. Q., and Luat, V. D. Nonlinear dynamic analysis and vibration of shear deformable piezoelectric FGM double curved shallow shells under damping-thermo-electromechanical loads. Composite Structures, 125, 29-40(2015) |
| [13] | Wali, M., Hentati, T., Jarraya, A., and Dammak, F. Free vibration analysis of FGM shell structures with a discrete double directors shell element. Composite Structures, 125, 295-303(2015) |
| [14] | Assaee, H. and Hasani, H. Forced vibration analysis of composite cylindrical shells using spline finite strip method. Thin-Walled Structures, 97, 207-214(2015) |
| [15] | Arefi, M. and Rahimi, G. H. Comprehensive thermoelastic analysis of a functionally graded cylinder with different boundary conditions under internal pressure using first order shear deformation theory. Mechanika, 18(1), 5-13(2012) |
| [16] | Arefi, M., Rahimi, G. H., and Khoshgoftar, M. J. Electro elastic analysis of a pressurized thickwalled functionally graded piezoelectric cylinder using the first order shear deformation theory and energy method. Mechanika, 18(3), 292-300(2012) |
| [17] | Liu, Y., and Chu, F. Nonlinear vibrations of rotating thin circular cylindrical shell. Nonlinear Dynamics, 67(2), 1467-1479(2011) |
| [18] | Ebrahimi, F. and Rastgo, A. An analytical study on the free vibration of smart circular thin FGM plate based on classical plate theory. Thin-Walled Structures, 46, 1402-1408(2008) |
| [19] | Ghorbanpour-Arani, A., Bakhtiari, R., Mohammadmehr, M., and Mozdianfard, M. R. Electromagnetomechanical responses of a radially polarized rotating functionally graded piezoelectric shaft. Turkish Journal of Engineering and Environment Science, 36, 33-44(2010) |
| [20] | Arefi, M., Rahimi, G. H., and Khoshgoftar, M. J. Exact solution of a thick walled functionally graded piezoelectric cylinder under mechanical, thermal and electrical loads in the magnetic field. Smart Structures and System, 9(5), 427-439(2012) |
| [21] | Fernandes, A. and Pouget, J. Structural response of composite plates equipped with piezoelectric actuators. Computers and Structures, 84, 1459-1470(2006) |
| [22] | Ghorbanpour-Arani, A., Shajari, A. R., Amir, S., and Loghman, A. Electro-thermo-mechanical nonlinear nonlocal vibration and instability of embedded micro-tube reinforced by BNNT, conveying fluid. Physica E, 45, 109-121(2012) |
| [23] | Patel, B. P., Gupta, S. S., Loknath, M. S., and Kadu, C. P. Free vibration analysis of functionally graded elliptical cylindrical shells using higher-order theory. Composite Structures, 69, 259-270(2005) |
| [24] | Yan, X. and Jinxi, L. Decay rate of Saint-Venant end effects for plane deformations of piezoelectric piezomagnetic sandwich structures. Acta Mechanica Solida Sinica, 23(5), 407-419(2010) |
| [25] | Rahimi, G. H., Arefi, M., and Khoshgoftar, M. J. Application and analysis of functionally graded piezoelectrical rotating cylinder as mechanical sensor subjected to pressure and thermal loads. Applied Mathematics and Mechanics (English Edition), 32(8), 997-1008(2011) DOI 10.1007/sl0483-011-1475-6 |
| [26] | Khoshgoftar, M. J., Arani, A. G., and Are, M. Thermoelastic analysis of a thick walled cylinder made of functionally graded piezoelectric material. Smart Materials and Structures, 18, 115007(2009) |
 2016, Vol. 37
2016, Vol. 37





