Nonlinear analysis on dynamic buckling of eccentrically stiffened functionally graded material toroidal shell segment surrounded by elastic foundations in thermal environment and under time-dependent torsional loads

http://dx.doi.org/10.1007/s10483-016-2099-9
Shanghai University

Article Information

D. V. DUNG, P. M. VUONG. 2016.

Appl. Math. Mech. -Engl. Ed., 37(7): 835-860

http://dx.doi.org/10.1007/s10483-016-2099-9

Article History

Received 2015-12-13;

in final form 2016-03-22

Citation

D. V. DUNG, P. M. VUONG. 2016. Nonlinear analysis on dynamic buckling of eccentrically stiffened functionally graded material toroidal shell segment surrounded by elastic foundations in thermal environment and under time-dependent torsional loads[J]. Appl. Math. Mech. -Engl. Ed., 37(7): 835-860. 复制到剪切板

D. V. DUNG¹, P. M. VUONG^2,

1. Department of Mathematics, Mechanics and Informatics, Vietnam National University, Hanoi 120160702, Vietnam;
2. Faculty of Civil and Industrial, National University of Civil Engineering, Hanoi 120160702, Vietnam

Received 2015-12-13; in final form 2016-03-22

Fund program: Project supported by the Vietnam National Foundation for Science and Technology Development (No. 107.02-2015.11)

Corresponding author: P. M. VUONG E-mail: phamminhvuongkhtn@gmail.com

ABSTRACT: The nonlinear analysis with an analytical approach on dynamic torsional buckling of stiffened functionally graded thin toroidal shell segments is investigated. The shell is reinforced by inside stiffeners and surrounded by elastic foundations in a thermal environment and under a time-dependent torsional load. The governing equations are derived based on the Donnell shell theory with the von Kármán geometrical nonlinearity, the Stein and McElman assumption, the smeared stiffeners technique, and the Galerkin method. A deflection function with three terms is chosen. The thermal parameters of the uniform temperature rise and nonlinear temperature conduction law are found in an explicit form. A closed-form expression for determining the static critical torsional load is obtained. A critical dynamic torsional load is found by the fourth-order Runge-Kutta method and the Budiansky-Roth criterion. The effects of stiffeners, foundations, material, and dimensional parameters on dynamic responses of shells are considered.

Keywords: toroidal shell segment functionally graded material (FGM) stiffened shell critical static and dynamic torsional load thermal environment

1 Introduction

Functionally graded material (FGM) is a material made of metal and ceramic. The highlights of FGM result from a combination of prominent characteristics of constituents such as high elasticity modulus, low thermal expansion, and conduction coefficients of ceramic and ductility of metal. By varying gradually the volume fractions of constituent materials, effective properties of FGM exhibit a smooth and continuous change from one surface to another, thus reducing or eliminating interface bond problems and huge stress concentration that are inherent in laminated composites. In recent, FGM structures are used efficiently in various engineering applications as pressure vessels, missiles, spacecraft, submarines, and nuclear reactors.

Due to importance of FGM structures in practical applications, the studies on the static and dynamic behaviors of FGM structures have attracted attention of many scientists. Many significant results have been obtained. Batra^[1] investigated the torsion of un-stiffened cylinders with material moduli varying only in the axial direction. Wang et al.^[2] presented an exact solution and transient behavior for torsional vibration of functionally graded finite hollow cylinder. Shen^[3] used the higher-order shear deformation theory (HSDT) and the singular perturbation technique to obtain the results on torsional loads and the post-buckling equilibrium paths of torsion-loaded FGM shells in thermal environments. Huang and Han^{[4, 5, 6, 7]}, with the three term deflection function, analyzed the buckling and post-buckling of un-stiffened FGM cylindrical shells under axial compressive load, radial pressure, and combined axial compressive load, and obtained the radial pressure based on the Donnell shell theory with the von K´arm´an geometrical nonlinearity and the Ritz method. By the same authors, the nonlinear dynamic buckling problems of un-stiffened functionally graded cylindrical shells subjected to time-dependent axial load by the one term solution form were investigated^[8]. Various effects of the inhomogeneous parameter, the loading speed, the dimension parameters “environmental temperature rise”, and the initial geometrical imperfection on nonlinear dynamic buckling were discussed in their works.

Sofiyev and Schnack^[9] investigated the stability of un-stiffened FGM cylindrical shells under linearly increasing dynamic torsional loading. The modified Donnell type dynamic stability equation and Galerkin method were used. However, the geometrical relation is linear, and the approximate solution was chosen by one-term.

For shells resting on elastic foundations, many studies have been focused on the buckling and post-buckling analysis of un-stiffened shells. Sheng and Wang^[10] considered the effect of thermal load on buckling, vibration, and dynamic buckling of un-stiffened FGM cylindrical shells embedded in a linear elastic medium based on the first-order shear deformation theory (FSDT) taking into account the rotary inertia and transverse shear strains. Also, based on the FSDT, Sheng and Wang^{[11, 12]} investigated thermoelastic vibration and buckling characteristic of the functionally graded piezoeletric cylindrical and analyzed response and control of functionally graded piezoeletric shells under thermal shock and moving loadings. Sheng and Wang^[13] studied dynamic characteristics of fluid, conveying functionally graded cylindrical shells under mechanical and thermal loads. Shen^[14] and Shen et al.^[15] presented the post-buckling analysis of FGM cylindrical shells surrounded by an elastic medium under the lateral pressure and axial load by the singular perturbation technique and the HSDT. Sofiyev and Avcar^[16] studied the stability of cylindrical shells containing an FGM layer subjected to axial load on the Pasternak foundation by the Galerkin method. By the same method, Sofiyev and Kuruoglu^[17] analyzed the torsional vibration and buckling of the un-stiffened cylindrical shell with functionally graded coatings surrounded by an elastic medium. Najafov et al.^[18] studied torsional vibration and stability of functionally graded orthotropic cylindrical shells on elastic foundation using the classical shell theory and the Galerkin method. Bagherizadeh et al.^[19] investigated the mechanical buckling of FGM cylindrical shells surrounded by the Pasternak elastic foundation based on the HSDT. Akbari et al.^[20] studied the thermal buckling of temperature-dependent FGM conical shells with arbitrary edge supports by an iterative generalized differential quadrature method. Bich and Tung^[21] presented an analytical approach to investigate nonlinear axisymmetric responses of FGM shallow spherical shells under uniform external pressure including temperature effects using the classical shell theory.

For revolution shells and toroidal shells, many interesting results on vibration and stability have been obtained. Stein and McElman^[22] studied static buckling of isotropic shallow segment of toroidal shell. Hutchinson^[23] analyzed initial post-buckling behavior of toroidal shell segments. Parnell^[24] reported a numerical improvement of asymptotic solutions for shells of revolution with application to toroidal shell segments. Using the theory of thin shells for deriving inhomogeneous Heun equations in a complex form, Chen^[25] presented exact solutions of toroidal shells in pressure vessels and piping under symmetric load. Wang and Zhang^[26] used the asymptotic solution to solve the problem on buckling of toroidal shells subjected to hydrostatic pressure based on Sander nonlinear equations of equilibrium. Zhang^[27] presented the complete asymptotic expansions of four homogeneous solutions and a particular solution of toroidal shells under nonsymmetric loadings based on Novozhilov thin shell equations. Zhu^[28] studied the vibration and stability of toroidal shells conveying fluid by the use of Love general thin shell equations and the classical flow theory. A general solution for the natural frequency was obtained in that work. Blachut and Jaiswal^[29] investigated the elastic and elastic-plastic buckling of geometrically perfect and imperfect toroidal shells under uniform external pressure by the numerical method. The geometrically nonlinear problems of in-plane pure bending of a toroidal shell of arbitrary cross-section were considered by Kuznetsov and Levyakov^[30]. A finite element algorithm for solution of the problem was proposed in their work. The free vibrations of elastic in vacuo circular toroidal shells under different boundary conditions were studied by Ming et al.^[31] using the Sander linear thin shell theory. Buchanan and Liu^[32] investigated the free vibration of thick-walled isotropic toroidal shells by the finite element method, in which the nine-node Lagrangian finite element was formulated in the toroidal coordinate system. Solutions were obtained for the case where an axis of symmetry can be assumed at the center of the torus. Asratyan and Gevorgyan^[33] solved mixed boundary-value problems of thermoelasticity for anisotropic-in-plan inhomogeneous toroidal shells by asymptotic integration of the equations of the three-dimensional problem of the anisotropic shell theory. Using the FSDT, Tornabene and Viola^[34] presented the static analysis of FGM doubly curved shells and panels of revolution by the generalized differential quadrature method.

For the FGM stiffened cylindrical shell, the stability problem is also a very interesting subject. Najafizadeh et al.^[35] used the linear stability equations in terms of displacements and studied buckling of FGM cylindrical shell reinforced by FGM rings and stringers under axial compression. By homogeneous stiffeners, Bich et al.^{[36, 37]} obtained the results on the nonlinear static and dynamic analysis of stiffened FGM imperfect doubly curved thin shallow shells and stiffened FGMcylindrical shells using the classical shell theory with the von K´arm´an geometrical nonlinearity and the smeared stiffeners technique. The nonlinear critical dynamic buckling load was found according to the Budiansky-Roth criterion. Dung and Hoa^{[38, 39]} obtained the results on the nonlinear static buckling and post-buckling analysis of eccentrically stiffened FGM (ESFGM) circular cylindrical shells under torsional and external loads without taking into account thermal elements. The material properties of shell and stiffeners are assumed to be continuously graded in the thickness direction. The Galerkin method was used to obtain the closed-form expression to determine critical buckling loads and load-deflection curve. Dung and Nam^[40] used the semi-analytical approach to present the nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under pressure and surrounded by an elastic medium without taking into account thermal elements.

The review of the literature signifies a problem, which has not been considered till today, i.e., the nonlinear analysis on dynamic buckling of ES-FGM toroidal shell segment surrounded by elastic foundation and subjected to dynamic torsional load in thermal environment.

This paper has new contributions. The shell under dynamic torsional load is a convex and concave toroidal shell segment, which is a general form for circular cylindrical shells. The shell is reinforced by closely spaced FGM stiffeners and attached to shell inside. The thermal elements of shell and stiffeners are taken into account. The thermal parameters of uniform temperature rise and nonlinear temperature conduction law are found in an analytical form. The deflection function with three-terms taking into account the nonlinear buckling shape is chosen more correctly. The closed-form expression for determining the static critical torsional load is obtained. The critical dynamic torsional load is determined using the Runge-Kutta method and the Budiansky-Roth criterion. The influence of various parameters such as the radius of longitudinal curvature, the stiffener, the foundation, the dimensional parameters, the volume fraction index of materials, and the temperature on the dynamic response of shell is analyzed.

The theoretical formulations based on the smeared stiffeners technique and the Donnell shell theory with the von K´arm´an geometrical nonlinearity, the Stein and McElman assumption, and the smeared stiffeners technique are derived. The resulting equations are solved by the Galerkin method to obtain nonlinear dynamic differential equations. When the radius of longitudinal curvature a→∞, we obtain results of the stiffened FGM cylindrical shell.

2 ES-FGM toroidal shell segment surrounded by elastic foundations

Assume that there is a plane circular arc of radius a (see Fig. 1(a) and Fig. 1(b)). Rotating this arc about an axis orthogonal to equator line in their plane, we obtain the middle surface of a shell of revolution called a segment of toroidal shell. If the curvature 1/a is positive, this shell is a convex shell (see Fig. 1(c)), in which k₁ is the Winkler foundation modulus characterizing the compressive resistance of foundation, k₂ is the shear layer foundation stiffness of the Pasternak model, b_s is the width of the stringer, z_s is the eccentricity of the stringer with respect to the middle surface of shell, d_s is the distance between two stringers, h_s is the thickness of the stringer, b_r is the width of ring, d_r is the distance between two rings, and h_r is the thickness of ring. If 1/a is negative, this shell is a concave shell (see Fig. 1(d)). If 1/a → 0, the shell becomes a cylindrical shell.

Fig. 1 Geometry and coordinate system of stiffened FGM toroidal shell segment

Figure options

Now, consider a segment of thin toroidal shell formed as was said above. The segment has the thickness h, the length L, and the radius of shell equator R, subjected to the torsional load of intensity τ. Assume that the shell is reinforced by closely spaced circular rings and longitudinal stringers attached to the inside of the shell. In addition, the stiffeners and skin are made of FGMs with Young’s modulus, the mass density, the thermal expansion coefficient, and the thermal conductivity coefficient varying continuously through the thickness direction of the shell with power laws as follows^{[35, 38, 41, 42]}:

For the shell,

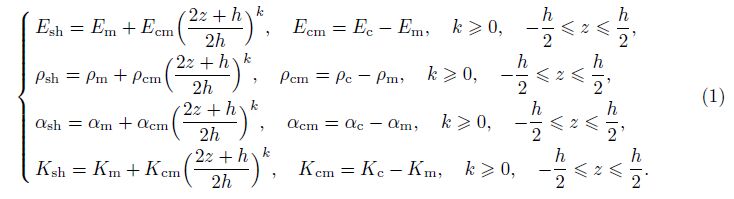
For the stringer,

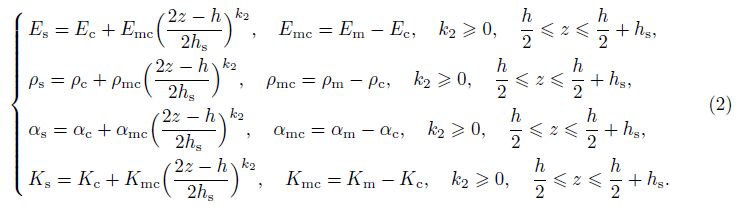
For the ring,

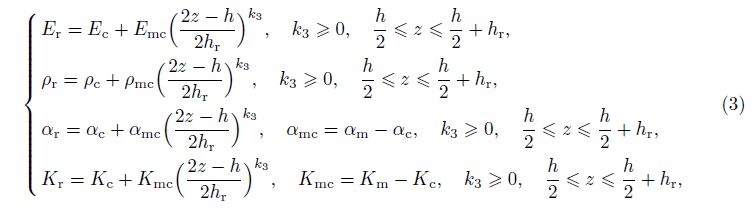
where k, k₂, and k₃ are the volume fraction indices of the shell, stringer, and ring, respectively, and the subscripts c, m, sh, s, and r denote ceramic, metal, shell, stringer, and ring, respectively. Note that h_s and h_r denote the thicknesses of the stringer and ring, respectively. E_sh, E_c, and E_m are Young’s moduli of the shell, ceramic, and metal, respectively. ρsh, ρc, and ρm are the mass densities of the shell, ceramic, and metal, respectively, αsh, αs, and αr are the thermal expansion coefficients of the shell, stringer, and ring, respectively, and K_sh, K_s, and K_r are the thermal conductivity coefficients of the shell, stringer, and ring, respectively.

It can be seen that, from Eqs. (1)-(3), a continuity between the shell and stiffeners is satisfied. In this study, Poisson’s ratios of shell, stringer, and ring are assumed to be constant, i.e., νsh = ν_s = ν_r = ν =const.

An elastic foundation is assumed as the Pasternark model^[43]. Therefore, the shell-foundation interaction is in the form of

where K₁ is the Winkler foundation modulus characterizing the compressive resistance of foundation, K₂ is the shear layer foundation stiffness of Pasternak model, w is the deflection of the shell, and ∇² is the Laplace operator. When K₂ = 0 from the Pasternak model, we can obtain the Winkler foundation model.

3 Theoretical derivation

It can be observed in Fig. 1(a) and Fig. 1(b), the radius of parallel circle R₀ is given by

where ϕ is the angle between the axis of revolution and the normal axis to the surface of shell.

Using the assumption of the shallowness of the toroidal shell along the meridian^{[21, 23, 41]}, the angle ϕ is approximate to π/2. Therefore, sin ϕ ≈ 1, cosϕ ≈ 0, and it leads to R₀ ≈ R. We can use a simpler coordinate as dx = adϕ and dy = Rdθ, where x and y are the axial and circumferential coordinates, respectively. Also, due to the shallowness of the toroidal shell, we can assume that the spacing between stringer stiffeners is constant.

According to the Donnell shell theory with the von K´arm´an geometrical nonlinearity^{[41, 42]} and the Stein and McElman assumption^[21], and Hutchinson^[23], the strain components at the middle surface of toroidal shell segment relating to the displacement components u, v, and w are in the forms of

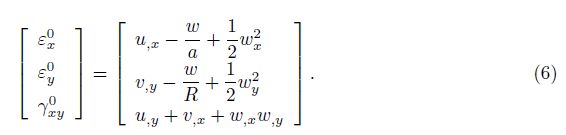
The strains across the shell thickness at a distance z from the middle surface are described as follows:

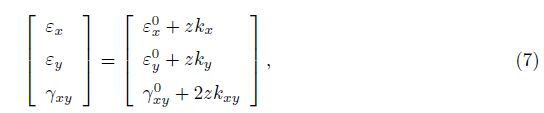
where k_x, k_y, and k_xy are the change of curvatures and twist of shell and defined as

From Eq. (6), the deformation compatibility equation for a toroidal shell segment is

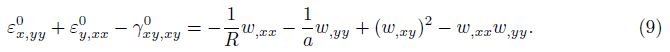
Applying Hooke’s law, the stress-strain relations taking into account the thermal element of shell and stiffeners are defined as follows.

For the toroidal shell segment,

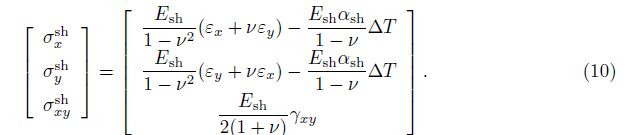
For the stringer and ring,

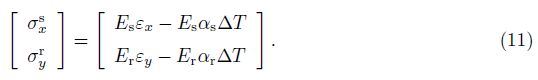
The contribution of stiffeners is accounted by the Lekhnitskii smeared stiffeners technique. Integrating the stress-strain equations and their moments through the thickness of the shell, the expressions for force and moment resultants of an ES-FGM toroidal shell segment are obtained as follows^{[35, 38, 41]}:

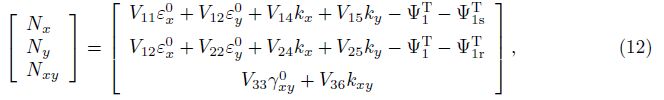
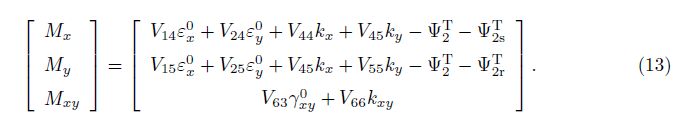
Equations (5) and (6) are our most significant established relations for an ES-FGM toroidal shell segment, where the coefficients V_ij and the thermal parameters Ψ^T₁, Ψ^T₂, Ψ^T_1s, Ψ^T_1r, Ψ^T_2s, and Ψ^T_2r are defined in Appendix A.

The strain-force reverse relations are found from Eq. (12) as

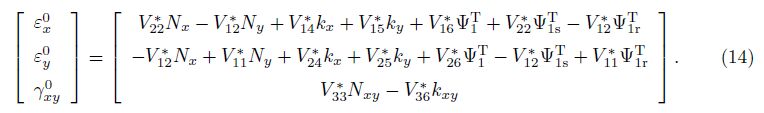
Substituting these relations into Eq. (13), we obtain

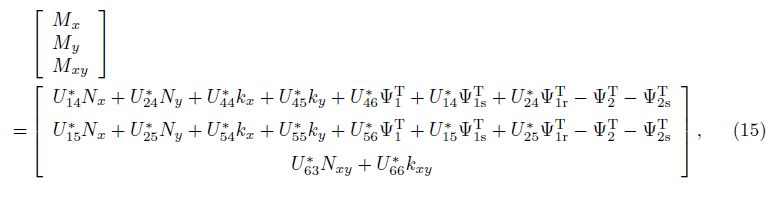
where the coefficients V ^* _ij and U^* _ij are determined in Appendix B.

The nonlinear motion equations of a toroidal shell segment using the Donnell shell theory and taking into account an elastic foundation and the assumption^{[31, 32, 44]}

are given by^{[28, 29, 38, 39, 41]}

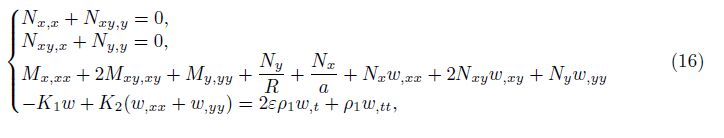
where

in which A₁ and A₂ are cross-section areas of stringer and ring, respectively, and ε is a damping coefficient.

It can be seen that the first two equations of Eq. (16) are automatically satisfied with the stress function F = F(x, y) as follows:

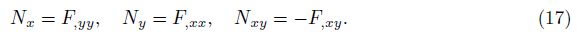
Substituting M_ij and N_ij from Eqs. (15) and (17) together with kij from Eq. (8) into the third equation of Eq. (16), we have

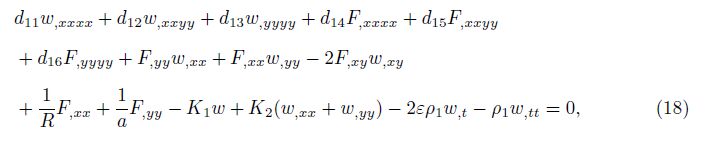
where

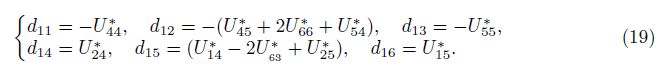
Because Eq. (18) includes two dependent unknown functions w and F, it is necessary to find a second equation relating to these two functions. For that, we use the geometrical compatibility equation (9). Setting Eq. (14) into Eq. (9), after some calculations, we obtain

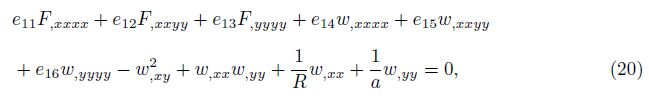
where

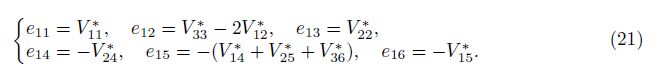
Equations (18) and (20) are two important governing equations used to investigate the vibration and nonlinear dynamic stability of ES-FGM toroidal shell segments surrounded by elastic foundations and subjected to time-dependent torsion loads. These governing equations are not only used to analyze the stability for the convex toroidal shell segment but also for the concave toroidal shell segment. These coupled nonlinear equations are more complex and more general than those of the cylindrical shell by the longitudinal curvature 1/a. The quality 1/a is taken positive value for a convex toroidal shell segment and negative value for a concave toroidal shell segment. When 1/a → 0, Eqs. (18) and (20) return to the equations of cylindrical shell.

4 Dynamic Galerkin method approach

Suppose that the ES-FGM toroidal shell segment is simply supported and subjected to uniformly distributed torsional load of intensity τ. Thus, the boundary conditions are written as

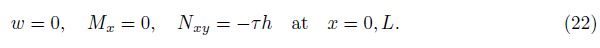
The deflection function w satisfying the above boundary conditions on the average sense is assumed to take three terms as^{[4, 44]}

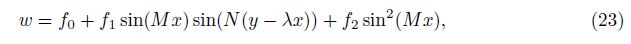
where is a time dependent uniform unknown amplitude of the prebuckling state, f₁ = f₁(t) is a time dependent linear unknown amplitude of the post-buckling state, f₂ = f₂(t) is a time dependent nonlinear unknown amplitude of the post-buckling state, m is a number of half wave in the axial direction, and n is a number of wave in the circumferential direction of the shell.

Substituting the expression of w from Eq. (23) into Eq. (20) yields the equation to determine unknown function F as

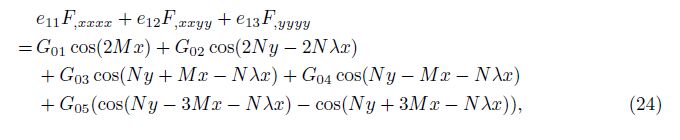
where

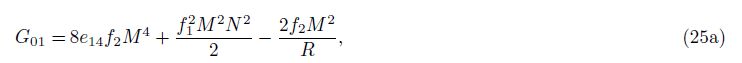
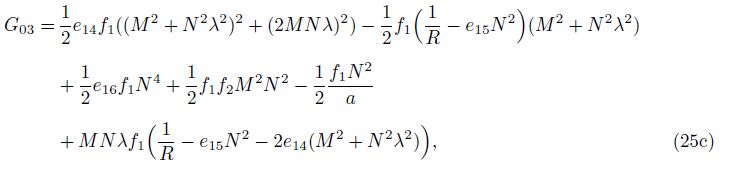
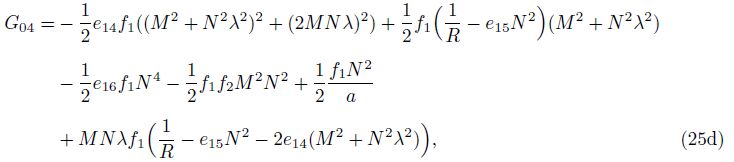
The general solution of this equation can be found in the form of

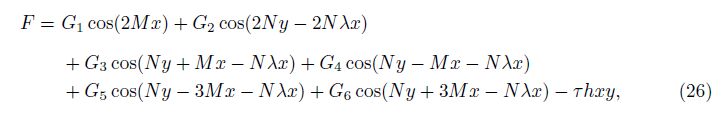
where G_i (i = 1, 2,…, 6) are defined in Appendix C.

In order to establish the torsional load-deflection relations, we apply the Galerkin method. First of all, introducing w and F into the left-hand side of Eq. (18) and then applying the Galerkin method for the remaining equation in the ranges 0 ≤ y ≤ 2πR and 0 ≤ x ≤ L lead to

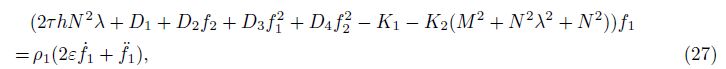
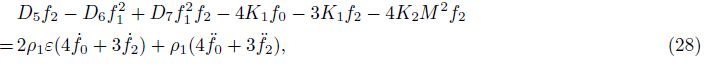
where

The coefficients D_i are defined in Appendix C.

Because the toroidal shell segment is a closed circular shell, it must satisfy the circumferential closed condition^{[4, 5, 6, 44]},

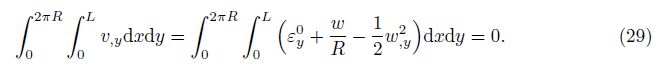
Using Eqs. (14), (8), (17), (23), and (26), this integral leads to

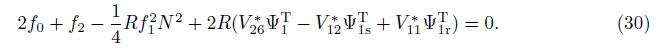
From Eq. (30), solving f₀ with respect to f₁ and f₂, then substituting it into Eq. (28), we have

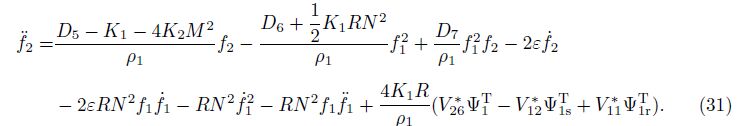
Equations (27) and (31) are nonlinear differential equations consisting of two unknown functions f₁ and f₂.

The maximal deflection of the shell is defined from Eq. (23) as

which is located at x = iL/(2m), and y = jπR/(2n)+iλL/(2m), where i and j are odd integer numbers.

From Eq. (30), representing f0 via f1 and f2, and introducing into Eq. (32) lead to

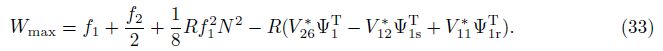
Using Eqs. (27) and (31) with Eq. (33), the critical dynamic torsional load and load-maximal deflection curves and the effects of the material properties, the dimensional parameters, the stiffener, the foundation, and the loading speed on the stability of shells are investigated in the numerical computational section.

When a→∞, these equations return to those of cylindrical shells.

The angle of twist for ES-FGM toroidal shell segments is defined^[44] as

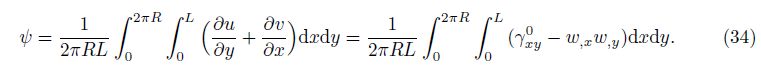
Using Eqs. (14) and (17), this integral becomes

Substituting w and F from Eqs. (23) and (26) and V ^*₃₃ into this equation yields

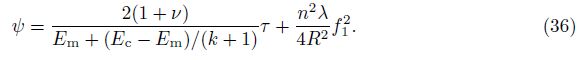
Combining Eqs. (27) and (31) together with Eq. (36), the τ-ψ twist angle-torsional load relation of shells will be studied.

Equations (27) and (31) are the nonlinear second-order differential equation system, and the mathematical difficulty is in the analytical solution. Therefore, for the dynamic buckling analysis, the Runge-Kutta numerical integration method and the Budiansky-Roth criterion are applied.

Assume a shell subjected to torsional load linearly varying on time τ = Ct, in which C is a loading speed (MPa/s). The critical dynamic torsional load τ_crd can be obtained according to the Budiansky-Roth criterion as follows^{[8, 9, 36, 40, 44, 45]}.

Under the action of dynamic load, the deflection of structure increases progressively with the increase of time. If the amplitude of deflection increases suddenly, the structure is instability. The time corresponding to this sudden jump is called the critical dynamic time t = t_crd, and the corresponding load τ_crd = Ct_crd is the critical dynamic buckling load.

Graphically, the slope of deflection amplitude-time (W_max-t) curve increases rapidly and reaches the first maximal point. Thus, unlike the static instability in which there is a definite point of instability, in the dynamic instability, there exists a region of instability during the initial time of sudden jump to the latest time at the first maximal point of deflection amplitudetime curve. Therefore, the dynamic critical time can be taken by a certain value in this region.

This paper uses the method proposed by Huang and Han^[8] with the instability point that satisfies the condition , and the dynamic critical load corresponding to this critical time is investigated numerically by τ_dcr = Ct_dcr.

5 Temperature 5.1 Uniform temperature rise

In this subsection, we assume that the environment temperature is uniformly raised from an initial value Ti to a final value Tf , and the temperature difference ΔT = T_f - T_i is a constant. The thermal parameters of the shell, the stringer, and the ring in this case can be found, respectively, in terms of ΔT as follows:

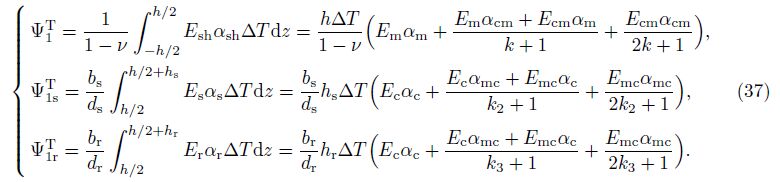
Combining Eq. (37) with Eqs. (27) and (31), the effects of the uniform temperature rise of the shell and the stiffener on static and dynamic responses of shells are investigated.

5.2 Nonlinear temperature change across thickness of shell

In this subsection, we consider the temperature changing in the thickness direction with the one-dimensional Fourier steady-state heat conductivity law. The thermal conductivity equation in the shell is established in a cylindrical coordinate system whose origin is on the symmetric axis of the cylinder rather than on the middle surface of the cylindrical shell^[46],

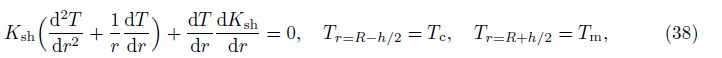
where r = R - z is the radial coordinate of the point which is the distant z from the middle surface of the shell respect to the symmetric axis of the cylinder. The quantities T_c and T_m are the temperatures at the ceramic-rich surface and the metal-rich surface, respectively.

Integrating Eq. (38), we can obtain the analogical result as^[21]

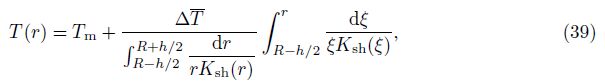
where is defined as the temperature difference between the ceramic-rich and metal-rich surfaces of the FGM toroidal shell.

Integrating of Eq. (39) has mathematical difficulty. This section only considers the linear distribution of ceramic and metal constituents, i.e., k =1 and

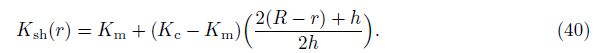
Substituting Eq. (40) into Eq. (39) and integrating the resulting equation yield the temperature distribution across the thickness z of shell as follows:

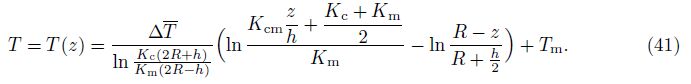
Using T (z) from Eq. (41) and substituting ΔT (z) = T (z) - T_m into the expressions of temperature parameters of shell in Appendix A, we obtain

in which

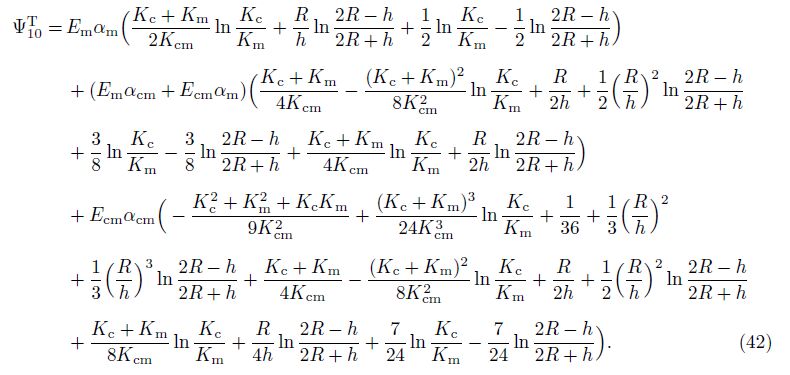
By the same method, with the linear thermal conductivity coefficients K_s and K_r, we also obtain the explicit expressions of thermal parameters of stringers and rings as follows:

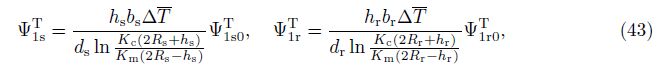
in which

Equations (42) and (43) are new results which we have found analytically. Combining Eqs. (42) and (43) with Eqs. (27) and (31), the effects of nonlinear temperature change across the thickness of shell on static and dynamic responses of shells are analyzed.

6 Static buckling problem

In this case, Eqs. (27), (28), and (30) must be taken as , and . To establish explicit expressions of static buckling, first eliminating f₀ and f₂ from those equations and then solving τ with respect to f₁ lead to the equation representing the τ-f₁ torsional load-deflection amplitude relation as

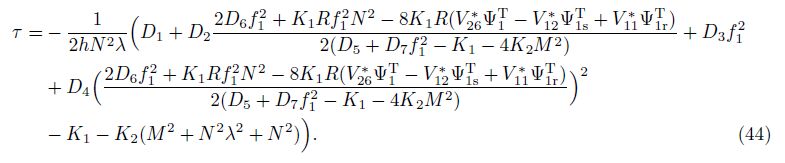
If K₁ = K₂ = 0 and the thermal element is ignored, Eq. (44) yields

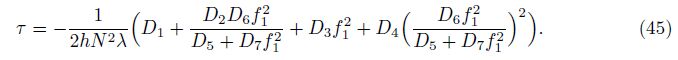
When a→∞, Eq. (45) coincides with the one reported in Ref. ^[38]. Taking f1 → 0, Eq. (45) becomes

and Eq. (44) reduces to

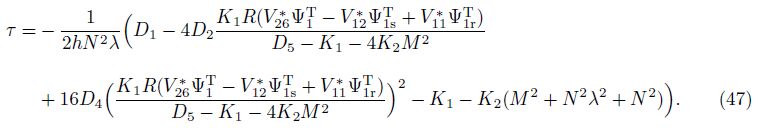
Equations (44)-(47) are explicit expressions used to find critical static torsional loads for ES-FGM toroidal shell segments without and with elastic foundations and without and with temperature.

7 Numerical results and discussion 7.1 Validation of present study

To verify the accuracy of present approach, three comparisons are considered below.

Table 1, using Eq. (46) with a→∞, compares the static critical torsional load for the unstiffened FGM cylindrical shell without foundation and under torsional load with the results given by Huang and Han^[4] and Sofiyev and Kuruoglu^[17]. The input parameters are taken as

Table 1 Comparisons of static critical torsional loads τ_crs for un-stiffened FGM cylindrical shell without foundation

Table options

Table 2 compares the results of this paper for the un-stiffened isotropic cylindrical shell without foundation and under static torsion load with the results given by Shen^[3] using the HSDT and with the experimental results of Nash^[47].

Table 2 Comparisons of static critical torsional load τ_crs for un-stiffened isotropic cylindrical shell

Table options

Table 3 compares the results of the present work for an ES-FGM cylindrical shell under the torsional load with those of Ref. ^[38]. The input parameters are given as k = k₂ = k₃ = 1, L = 387.35 × 10^-3 m, h_s = h_r = h/2, b_r = b_s = h/2, E_c = 151 GPa, and E_m = 70 GPa.

Table 3 Comparisons of static critical torsional load τ_crs for ES-FGM cylindrical shell

Table options

It can be seen that good agreement is obtained in these comparisons.

In the subsections below, consider a shell with geometric and material properties as follows:

7.2 Effectiveness of reinforcement stiffeners

In order to demonstrate the effectiveness of reinforcement stiffeners, we consider five cases for cylindrical shells (with the same volume of materials V = 0.032 169 9 m³): an un-stiffened shell, a stiffened shell with stringers n_s=15 and rings n_r=15, a stiffened shell with stringers n_s=15, a stiffened shell with rings n_r=15, and a stiffened shell with rings n_r=30. The input parameters are given as

Using Eqs. (44) and (47), we obtain static critical loads for un-stiffened shell and stiffened shells as shown in Table 4.

Table 4 Effectiveness of reinforced stiffeners

Table options

It can be observed that with the same volume of materials, the static critical load is the largest for the stiffened shell with n_s=0, n_r=30; next for the case n_s=0, n_r=15; next for the case n_s=15, n_r=15; and the static critical load for the un-stiffened shell is the smallest. The obtained results affirm the effectiveness of reinforcement stiffeners. The loading carrying capacity of shell increases when the shells are reinforced.

7.3 Effects of longitudinal curvature radius a on critical torsional loads

Consider a toroidal shell with material and geometric properties as Subsection 7.2 and R/h=100, h_s =h_r =0.008 m, b_s =b_r =0.003 m, and n_s =n_r =15. The radius of longitudinal curvature a varies.

The effects of longitudinal curvature radius a on static and dynamic critical loads are given in Table 5 and Fig. 2. It is observed the critical torsional load decreases when a increases. The convex toroidal shell (a > 0) subjected to torsional loads is better than the concave torsional shell (a < 0). For example, τ_crs=589.407 8 MPa (a=2, ΔT =0) is about 2.5 times of τ_crd=233.081 1 MPa (a = -2, ΔT =0).

Table 5 Effects of curvature radius a on static and dynamic critical torsional loads

Table options

Fig. 2 Effects of radius a on dynamic critical torsional loads

Figure options

7.4 Effects of temperature on critical torsional loads

The effects of uniform temperature rise and change of nonlinear temperature on static and dynamic critical torsional loads of toroidal shell are presented in Table 6. The input parameters are taken as in Subsection 7.3, but a=5 m, K_m = 204 W/(m·K), and K_c = 10.4 W/(m·K). It can be seen that the static and dynamic torsional loads decrease with the increase of ΔT. In addition, the static and dynamic torsional loads for the nonlinear temperature are larger than those for the uniform temperature rise.

Table 6 Effects of temperature on critical torsional loads

Table options

7.5 Effects of ratio R/h on critical torsional loads

Table 7 and Fig. 3 illustrate effects of the radius-to-thickness ratio R/h on the static and dynamic critical torsional loads of toroidal shell using the database in Subsection 7.2 and a=5 m, h_s = h_r = h, b_s = b_r = h, n_s = n_r =15, and R=0.8 m. The ratio R/h varies from 100 to 500.

Table 7 Effects of ratio R/h on static and dynamic critical torsional loads

Table options

Fig. 3 Effects of ratio R/h on dynamic critical torsional loads

Figure options

It is clear that the critical torsion load decreases when the ratio R/h increases. These characteristics are adequate to true property of shell. It means that the shell is thinner, and the critical buckling load is smaller. In addition, the critical load decreases strongly when the ratio R/h varies from 100 to 200. However, with the ratio R/h varying from 400 to 500, the critical load decreases more slowly.

7.6 Effects of volume fraction indices k, k2, and k3 on critical torsional loads

Table 8 and Fig. 4 describe the effects of volume fraction indexes k, k₂, and k₃ on the critical load of the shell. The input parameters are chosen as in Subsection 7.2 and a=5 m, R/h=100, L/R=2, h_s = h_r =0.008 m, b_s = b_r =0.003 m, and n_s = n_r =15. The indexes k, k₂, and k₃ vary.

Table 8 Effects of k and k₂=k₃=1/k on static and dynamic critical loads

Table options

Fig. 4 Effects of k on dynamic critical torsional loads

Figure options

It is seen that the critical torsional loads of shells decrease with the increase of k. This property appropriates to the real characteristic of material, because the higher value of k corresponds to a metal-richer shell which usually has less stiffness than a ceramic-richer shell. This decrease is significant. For example, from Table 9, τ_crd =464.176 5 MPa (k=0.5) is larger than τ_crd =387.032 0 MPa about 16.6%.

Table 9 Effects of K₁ and K₂ on static and dynamic critical torsional loads

Table options

7.7 Effects of elastic foundation parameters on critical torsional loads

By the same input parameters as Subsection 7.2 and a=5 m, h=h_s=h_r=0.008 m, R/h=100, b_s = b_r =0.003 m, and n_s = n_r =15, Table 9 and Fig. 5 show the effects of elastic foundation parameters K₁ (N/m³) and K₂ (N/m) on the critical torsional loads of shell.

Fig. 5 Effects of elastic foundation parameters on dynamic critical torsional loads

Figure options

It is found that the presence of foundations increases the carrying capacity of shells. In addition, the critical torsional load corresponding to the contribution of both two foundation parameters is the largest. It seems that K2 affects the critical load more strongly than K₁. We also see that the critical torsional load of shell without foundation is the smallest. The difference between the critical loads of the shell with foundation and the shell without foundation is significant. For example, from Table 10, τ_crd =434.759 8 MPa (K₁ = 1.5 × 10⁷N/m³ and K² = 1.5×10⁵ N/m) is larger than τ_crd =397.327 6 MPa of the shell without foundation about 8.6%.

7.8 Effects of stiffener number on critical torsional loads

Table 10 and Fig. 6 show the effects of the stiffener number on the critical torsional loads of shell using the input parameters of Subsection 7.2 and a=5 m, h = h_s = h_r =0.008 m, R/h=100, b_s = b_r =0.003 m.

Table 10 Effects of stiffener number on static and dynamic critical torsional loads

Table options

Fig. 6 Effects of stiffener number on dynamic critical torsional loads

Figure options

It can be seen that the critical torsional loads increase with the increase of the stiffener number. The critical loads corresponding to the presence of rings are the largest. However, the critical loads of un-stiffened shells are the smallest. These results affirm once again on the effectiveness of reinforcement stiffeners. The increase of the critical torsional load of stiffened shell is significant. For example, τ_crd =460.279 MPa of the stiffened shell (n_s=0, n_r=30) is larger than τ_crd =401.823 8 MPa of the un-stiffened shell about 12.7%.

7.9 Effects of temperature, foundation, and index volume fraction on τ-ψ curves

Figure 7 describes the effects of foundation parameters on τ-ψ curves. It can be observed that during the first stage, these curves increase linearly with the increase of foundation parameters. However, in the second stage, they vary nonlinearly. The larger K₁ and K₂ are, the higher the curves are.

Fig. 7 Effect of foundation on τ -ϕ curves (m=1)

Figure options

Figure 8 shows the effects of the volume fraction indexes k and k₁ = k₂ = 1/k on the τ-ϕ curves. Graphs are plotted with k=0, 0.5, 1, 5. We can see that these curves become to be down gradually when the value of k increases. In addition, with the same value of load, the twist angle decreases when k increases.

Fig. 8 Effects of k on τ -ϕ

Figure options

Figure 9 shows the effects of the thermal element on the τ-ϕ curves. Graphs are plotted for ES-FGM shells without and with temperature. The static critical torsional load of shell decreases when ΔT increases. This phenomenon is suitable to true property of shell. The higher the shell subjected to temperature is, the weaker its loading carrying capacity is.

Fig. 9 Effects of L/R and ΔT on τ -ϕ curves (m=1)

Figure options

Figure 9 also shows the effects of the ratio L/R on the τ-ϕ curves. We can see that the static critical torsional load of shell decreases when the ratio L/R increases.

8 Concluding remarks

An analytical approach to analyze the nonlinear static and dynamic torsional behavior of ES-FGM toroidal shells surrounded by elastic foundations and under dynamic torsional load and in the thermal environment is studied in this paper. The shells are assumed to be stiffened by eccentrically FGM rings and stringers. Material properties of shell and stiffeners vary continuously in the thickness direction. The elastic foundation is assumed as the Pasternak twoparameter elastic foundation model. Based on the Donnell shell theory with the von K´arm´an geometrical nonlinearity, the Lekhniskii smeared the stiffeners technique, and the Galerkin method, the governing equations are derived. Some main results are reached.

(i) The deflection function with three-terms taking into account the nonlinear buckling shape is chosen satisfying simply supported boundary conditions at the butt-ends of the shell.

(ii) The analytical expressions of thermal parameters for the shell, the stringers, and the rings are obtained.

(iii) The twist angle-torsional-load relation is obtained in the explicit form.

(iv) The dynamic critical torsional load is found by the fourth-order Runge-Kutta method and the Budiansky-Roth criterion.

(v) The analytical expression for determining the static critical torsional load is obtained.

(vi) The effects of the radius of longitudinal curvature a, the stiffeners, the foundations, the temperature, the material, and the dimensional parameters on static and dynamic responses of the shells are considered by numerical calculations.

Appendix A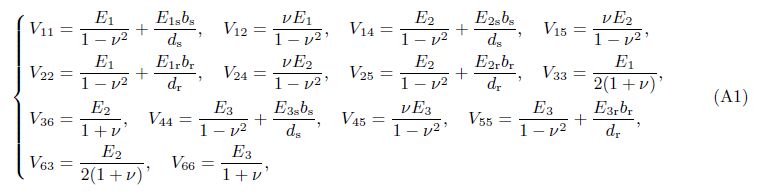

in which for the shell,

If ΔT is constant, then

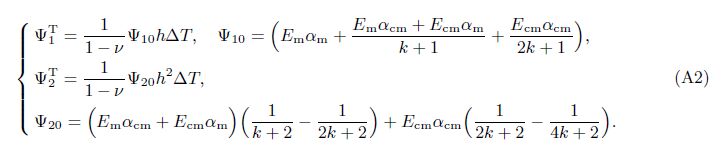
For stringers,

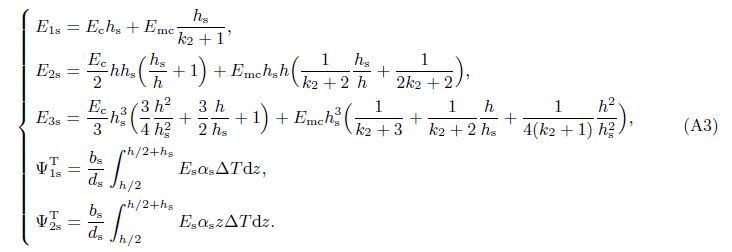
For rings,

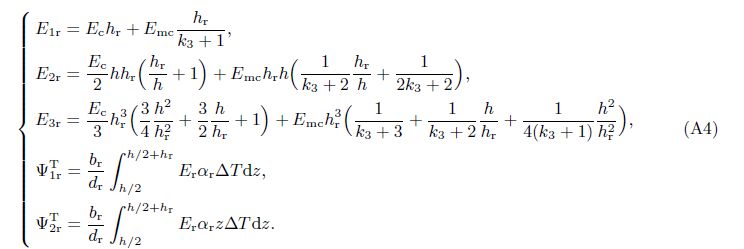
If ΔT is constant, then

Appendix B

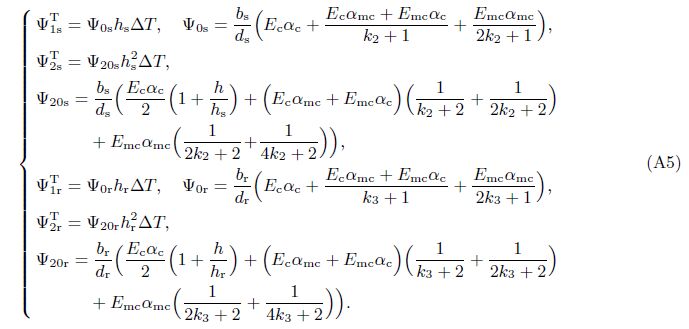
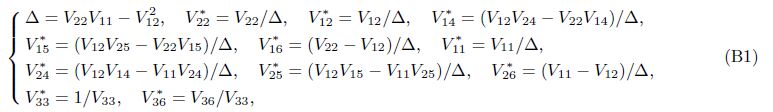
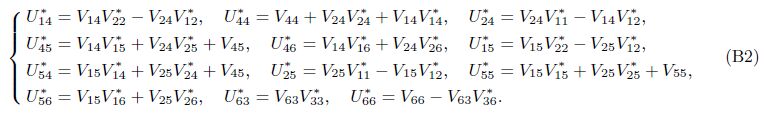
Appendix C

in which

References

[1]	Batra, R. C. Torsion of a functionally graded cylinder. AIAA Journal, 44, 1363-1365(2006)

[2]	Wang, H. M., Liu, C. B., and Ding, H. J. Exact solution and transient behavior for torsional vibration of functionally graded finite hollow cylinders. Acta Mechanica Sinica, 25, 555-563(2009)

[3]	Shen, H. S. Torsional buckling and postbuckling of FGM cylindrical shells in thermal environments. International Journal of Non-Linear Mechanics, 44, 644-657(2009)

[4]	Huang, H. and Han, Q. Nonlinear buckling of torsion-loaded functionally graded cylindrical shells in thermal environment. European Journal of Mechanics-A/Solids, 29, 42-48(2010)

[5]	Huang, H. and Han, Q. Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells. International Journal of Mechanical Sciences, 51, 500-507(2009)

[6]	Huang, H. and Han, Q. Nonlinear buckling and postbuckling of heated functionally graded cylindrical shells under combined axial compression and radial pressure. International Journal of Non-Linear Mechanics, 44, 209-218(2009)

[7]	Huang, H. and Han, Q. Research on nonlinear postbuckling of FGM cylindrical shells under radial loads. Composite Structures, 92, 1352-1357(2010)

[8]	Huang, H. and Han, Q. Nonlinear dynamic buckling of functionally graded cylindrical shells subjected to a time-dependent axial load. Composite Structures, 92, 593-598(2010)

[9]	Sofiyev, A. and Schnack, H. E. The stability of functionally graded cylindrical shells under linearly increasing dynamic torsional loading. Engineering Structures, 26, 1321-1331(2004)

[10]	Sheng, G. G. and Wang, X. Thermal vibration, buckling and dynamic stability of functionally graded cylindrical shells embedded in an elastic medium. Journal of Reinforced Plastics and Composites, 27, 117-134(2008)

[11]	Sheng, G. G. and Wang, X. Thermoelastic vibration and buckling analysis of functionally graded piezoelectric cylindrical shells. Applied Mathematical Modelling, 34, 2630-2643(2010)

[12]	Sheng, G. G. and Wang, X. Response and control of functionally graded laminated piezoelectric shells under thermal shock and moving loadings. Composite Structures, 93, 132-141(2010)

[13]	Sheng, G. G. and Wang, X. Dynamic characteristics of fluid-conveying functionally graded cylindrical shells under mechanical and thermal loads. Composite Structures, 93, 162-170(2010)

[14]	Shen, H. S. Postbuckling of shear deformable FGM cylindrical shells surrounded by an elastic medium. International Journal of Mechanical Sciences, 51, 372-383(2009)

[15]	Shen, H. S., Yang, J., and Kitipornchai, S. Postbuckling of internal pressure loaded FGM cylindrical shells surrounded by an elastic medium. European Journal of Mechanics-A/Solids, 29, 448-460(2010)

[16]	Sofiyev, A. H. and Avcar, M. The stability of cylindrical shells containing a FGM layer subjected to axial load on the Pasternak foundation. Engineering, 2, 228-236(2010)

[17]	Sofiyev, A. H. and Kuruoglu, N. Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Composites Part B:Engineering, 45, 1133-1142(2013)

[18]	Najafov, A. M., Sofiyev, A. H., and Kuruoglu, N. Torsional vibration and stability of functionally graded orthotropic cylindrical shells on elastic foundations. Meccanica, 48, 829-840(2013)

[19]	Bagherizadeh, E., Kiani, Y., and Eslami, M. R. Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Composite Structures, 93, 3063-3071(2011)

[20]	Akbari, M., Kiani, Y., and Eslami, M. R. Thermal buckling of temperature-dependent FGM conical shells with arbitrary edge supports. Acta Mechanica, 226, 897-915(2015)

[21]	Bich, D. H. and Tung, H. V. Nonlinear axisymmetric response of functionally graded shallow spherical shells under uniform external pressure including temperature effects. International Journal of Non-Linear Mechanics, 46, 1195-1204(2011)

[22]	Stein, M. and McElman, J. A. Buckling of segments of toroidal shells. AIAA Journal, 3, 1704-1709(1965)

[23]	Hutchinson, J. W. Initial post-buckling behavior of toroidal shell segments. International Journal of Solids and Structures, 3, 97-115(1967)

[24]	Parnell, T. K. Numerical improvement of asymptotic solutions for shells of revolution with application to toroidal shell segments. Computers and Structures, 16, 109-117(1983)

[25]	Chen, G. D. Exact solutions of toroidal shells in pressure vessels and piping. International Journal of Pressure Vessels and Piping, 19, 101-115(1985)

[26]	Wang, A. W. and Zhang, W. Asymptotic solution for buckling of toroidal shells. International Journal of Pressure Vessels and Piping, 45, 61-72(1991)

[27]	Zhang, R. J. Toroidal shells under nonsymmetric loading. International Journal of Solids and Structures, 19, 2735-2750(1994)

[28]	Zhu, F. Vibration and stability analysis of toroidal shells conveying fluid. Journal of Sound and Vibration, 183(2), 197-208(1995)

[29]	Blachut, J. and Jaiswal, O. R. On buckling of toroidal shells under external pressure. Computers and Structures, 77, 233-251(2000)

[30]	Kuznetsov, V. V. and Levyakov, S. V. Nonlinear pure bending of toroidal shells of arbitrary cross-section. International Journal of Solids and Structures, 38, 7343-7354(2001)

[31]	Ming, R. S., Pan, J., and Norton, M. P. Free vibrations of elastic circular toroidal shells. Applied Acoustics, 63, 513-528(2002)

[32]	Buchanan, G. R. and Liu, Y. J. An analysis of the free vibration of thick-walled isotropic toroidal shells. International Journal of Mechanical Sciences, 47, 277-292(2005)

[33]	Asratyan, M. G. and Gevorgyan, R. S. Mixed boundary-value problems of thermoelasticity anisotropic-in-plane inhomogeneous toroidal shells. Journal of Applied Mathematics and Mechanics, 74, 306-312(2010)

[34]	Tornabene, F. and Viola, E. Static analysis of functionally graded doubly-curved shells and panels of revolution. Meccanica, 48, 901-930(2013)

[35]	Najafizadeh, M. M., Hasani, A. P., and Khazaeinejad, P. Mechanical stability of functionally graded stiffened cylindrical shells. Applied Mathematical Modelling, 33, 1151-1157(2009)

[36]	Bich, D. H., Dung, D. V., and Nam, V. H. Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures, 96, 384-395(2013)

[37]	Bich, D. H. Dung, D. V., Nam, V. H., and Phuong, N. T. Nonlinear static and dynamic buckling analysis of imperfect eccentrically stiffened functionally graded circular cylindrical thin shells under axial compression. International Journal of Mechanical Sciences, 74, 190-200(2013)

[38]	Dung, D. V. and Hoa, L. K. Research on nonlinear torsional buckling and post-buckling of eccentrically stiffened functionally graded thin circular cylindrical shells. Composites Part B:Engineering, 51, 300-309(2013)

[39]	Dung, D. V. and Hoa, L. K. Nonlinear buckling and post-buckling analysis of eccentrically stiffened functionally graded circular cylindrical shells under external pressure. Thin-Walled Structures, 63, 117-124(2013)

[40]	Dung, D. V. and Nam, V. H. Nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. European Journal of Mechanics-A/Solids, 46, 42-53(2014)

[41]	Brush, D. O. and Almroth, B. O. Buckling of Bars, Plates and Shells, McGraw-Hill, New York (1975)

[42]	Reddy, J. N. Mechanics of Laminated Composite Plates and Shells, Theory and Analysis, CRS Press, Boca Raton (2004)

[43]	Pasternak, P. L. On a New Method of Analysis of an Elastic Foundation by Mean of Two Foundation Constant, Gos Izd Lit Po Stroit Arkh, Moscow (1954)

[44]	Volmir, A. S. Stability of Elastic Systems, Science Edition, Moscow (1963)

[45]	Budiansky, B. and Roth, R. S. Axisymmetric dynamic buckling of clamped shallow spherical shells. NASA Technical Note, Washington, D. C., 597-609(1962)

[46]	Shariyat, M., Khaghani, M., and Lavasani, S. M. H. Nonlinear thermoelasticity, vibration, and stress wave propagation analyses of thick FGM cylinders with temperature-dependent material properties. European Journal of Mechanics-A/Solids, 29, 378-391(2010)

[47]	Nash, W. A. An experimental analysis of the buckling of thin initially imperfect cylindrical shells subject to torsion. Proceedings of the Society for Experimental Stress Analysis, 16(2), 55-68(1959)