Appl. Math. Mech. -Engl. Ed.   2016, Vol. 37 Issue (7): 861-878     PDF       
http://dx.doi.org/10.1007/s10483-016-2094-9
Shanghai University
0

Article Information

Xuan WANG, Shirong LI. 2016.
Free vibration analysis of functionally graded material beams based on Levinson beam theory
Appl. Math. Mech. -Engl. Ed., 37(7): 861-878
http://dx.doi.org/10.1007/s10483-016-2094-9

Article History

Received 2015-10-14;
in final form 2016-03-02
Citation
Xuan WANG, Shirong LI. 2016. Free vibration analysis of functionally graded material beams based on Levinson beam theory[J]. Appl. Math. Mech. -Engl. Ed., 37(7): 861-878.
Free vibration analysis of functionally graded material beams based on Levinson beam theory
Xuan WANG1, Shirong LI1,2        
1. School of Hydraulic, Energy and Power Engineering, Yangzhou University, Yangzhou 225127, Jiangsu Province, China;
2. School of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, Jiangsu Province, China
Received 2015-10-14; in final form 2016-03-02
Fund program: Project supported by the National Natural Science Foundation of China (No. 11272278)
Corresponding author: Shirong LI E-mail: srli@yzu.edu.cn
ABSTRACT: Free vibration response of functionally graded material (FGM) beams is studied based on the Levinson beam theory (LBT). Equations of motion of an FGM beam are derived by directly integrating the stress-form equations of elasticity along the beam depth with the inertial resultant forces related to the included coupling and higherorder shear strain. Assuming harmonic response, governing equations of the free vibration of the FGM beam are reduced to a standard system of second-order ordinary differential equations associated with boundary conditions in terms of shape functions related to axial and transverse displacements and the rotational angle. By a shooting method to solve the two-point boundary value problem of the three coupled ordinary differential equations, free vibration response of thick FGM beams is obtained numerically. Particularly, for a beam with simply supported edges, the natural frequency of an FGM Levinson beam is analytically derived in terms of the natural frequency of a corresponding homogenous Euler-Bernoulli beam. As the material properties are assumed to vary through the depth according to the power-law functions, the numerical results of frequencies are presented to examine the effects of the material gradient parameter, the length-to-depth ratio, and the boundary conditions on the vibration response.
Keywords: functionally graded material (FGM)beam     Levinson beam theory (LBT)     free vibration     shooting method     natural frequency    
1 Introduction

Functionally graded materials (FGMs) are one kind of new composites that have a smooth and continuous spatial variation of material properties which can alleviate the stress concentration found in laminated composites. The gradient compositional variation in the constituents from one surface to another provides a good way to solve the problem of higher transverse shear stresses induced when two similar materials with large difference in material properties are bonded. Therefore, FGMs have an enormous application potential in modern technology and engineering, such as mechanical, aerospace, nuclear, and civil engineering. Especially, in the thermal environments, it can minimize the thermal stress concentration produced by the high temperature gradient. In recent years, many efforts have been paid to various investigations of the mechanical behaviours of the FGM structures. A survey in the literature shows that many studies on free vibration of FGM beam structures based on different beam theories, such as the Euler-Bernoulli beam theory (EBBT), the Timoshenko beam theory (TBT), the Levinson beam theory (LBT), and the Reddy-Bickford beam theory (RBBT), have been made by different researchers.

On the basis of the EBBT, some authors studied vibration the responses of FGM beams by different analytical and numerical approaches[1, 2, 3, 4, 5, 6, 7, 8, 9]. Alshorbagy et al.[1] investigated free vibration of an FGM beam by the finite element method. Due to the deficiency in the EBBT for consideration of the shear effect, the numerical results showed that the slenderness of the beam has no influence on the frequencies and mode shapes. S¸im¸sek and Kocat$\ddot u$rk[2] studied dynamic response of an FGM beam under a concentrated moving load, in which the effects of the material gradient, the velocity of the moving harmonic load, and the excitation frequency on the dynamic responses of the beam were discussed. The same problem was also investigated by Khalili et al.[3] using a mixed Ritz-differential quadrature (DQ) method. Pradhan and Murmu[4] presented a numerical research on thermo-mechanical vibration of a simply supported sandwich beam with two FGM surface layers, resting on an axially variable elastic foundation and subjected to a transversely non-uniform temperature rise by the differential quadrature method (DQM). By assuming the material properties changing in the thickness direction, free vibration and buckling of FGM beams with vertical edge cracks were analyzed by Yang and Chen[5]. Effects of the parameters of material gradient, location and numbers of the cracks, and the boundary conditions on the natural frequencies and buckling loads were examined. Li and Liu[6] showed that the deflections, the critical buckling loads, and the natural frequencies of FGM beams are proportional to those of the reference homogenous beams and proved that these relationships are independent of the load and boundary conditions. Li et al.[7] performed a small free vibration of thermo-electrically post-buckled FGM beams with surface-bonded piezoelectric layers in thermal environment by a numerical shooting method based on the exact geometrically nonlinear theory for the axially extensible beams. Huang and Li[8] studied free vibration of axially functionally graded beams with non-uniform cross-section using an integration technique to transform the differential governing equations into Fredholm integral equations. More recently, Liu and Shu[9] presented an analytical solution for the free vibration of exponential functionally graded beams with a single delamination, in which the ‘free mode’ and ‘constrained mode’ assumptions in delamination vibration were adopted.

In the framework of the first-order shear deformation theory, or the TBT, other researchers dealt with the dynamic response of FGM beams[10, 11, 12, 13, 14, 15, 16, 17, 18, 19]. Sina et al.[10] used a new beam theory different from the traditional first-order shear deformation beam theory to analyze the free vibration of FGM beams. By introducing a new unknown function to decouple the governing equations, Li[11] presented analytical solutions for the bending and free vibration of FGM Timoshenko beams. Pradhan and Chakraverty[12] carried out an investigation on free vibration of FGM beams by the Rayleigh-Ritz method based on both classical and first-order shear deformation beam theory considering Poisson’s ratio effect in the axial stress-strain relation. The free and forced vibration of a laminated functionally graded beam of variable thickness under thermally induced initial stress was studied by Xiang and Yang[13] using the DQM. By the finite element method, Shahba et al.[14] examined free vibration analysis of axially functionally graded tapered beams with classical and non-classical boundary conditions. Huang et al.[15] investigated the free vibration of both geometrically and physically non-homogenous beams, in which the authors introduced a similar auxiliary function as in Ref. [11] to decouple the governing differential equations and obtained a polynomial form solution of the reduced ordinary differential equation with variable coefficients. Analytical solution for static buckling and free vibration of simply supported FGM beams subjected axial load were obtained by Nguyen et al.[16], where the effects of axial load parameter on the natural frequency were examined quantitatively. More recently, Rajasekaran and Tochaei[17] used both the differential transformation element method (DTEM) and the differential quadrature element method (DQEM) to carry out the free vibration analysis of axially functionally graded tapered beams. By the DQEM, Li and Fan[18] studied free vibration of FGM beams with a through-width delamination. Numerical results of the first eight natural frequencies of the delaminated FGM beam with clamped-clamped ends were presented to show the effects of the parameters of the material gradients and the size and location of the delamination on the vibration responses. Li et al.[19] also studied free vibration of FGM beams based on both classical and Timoshenko beam theories by a shooting method. An analytical and proportional transition relation between the natural frequency of FGM beams and that of the homogenous ones were derived based on the classical beam theory.

In order to get higher accuracy in taking into account the transverse shear deformation, studies on free vibration of FGM beams were performed based on the higher-order shear deformation beam theory[20, 21, 22, 23, 24, 25, 26, 27, 28]. Based on the first, parabolic, and exponential shear deformation beam theories, Aydogdu and Taskin[20] studied free vibration of a simply supported FGM beam and obtained natural frequencies using the Navier type solution method. S¸im¸sek[21, 22] investigated dynamic responses of FGM beams based on different shear deformation beam theories, in which motion equations were derived using Lagrange’s equations. Mahi et al.[23] analyzed free vibration of FGM beams with the temperature dependent material properties. The effects of the initial thermal stress on the natural frequencies were also discussed. Pradhan and Chakraverty[24] investigated free vibration response of FGM beams under different boundary conditions based on different higher-order shear deformation beam theories using the Rayleigh-Ritz method. In the stress-strain relation, the Poisson’s ratio effect on the axially normal stress was taken into account. Analytical solution in trigonometric series form for static bending and free vibration of simply supported FGM beams was presented by Thai and Vo[25] using various higher-order shear deformation theories. Numerical results were given to examine the effects of different theories on the static and dynamic responses. More recently, Vo et al.[26, 27] investigated static bending, buckling, and free vibration of FGM beams based on the refined shear deformation beam theory (a kind of higher-order beam theory) using the finite element method. The effects of the material gradient parameter, the length-to-depth ratio, and the boundary conditions on the deflection, buckling loads, and natural frequency were discussed in detail through the giving plentiful numerical results. Shen and Wang[28] carried out geometrically nonlinear analysis for vibration, bending, and thermal buckling of FGM beams resting on an elastic foundation in thermal environment based on the higher-order shear deformation theory and incorporated von Karman’s nonlinear strain-displacement relation. In the prediction of the effective material properties in the FGM beam, two kinds of micromechanics models, namely, the Voigt model and the Mori-Tanaka model, were used.

In this paper, free vibration of FGM beams is investigated based on the LBT by the numerical shooting method. In the displacement field of the LBT[29, 30], the higher-order variation of the axial displacement through the beam depth is assumed to accurately satisfy the condition of shear stress on the top and bottom surfaces and to avoid the use of shear correction factor in the TBT. Different from the derivation of equations of motion by Hamilton’s principle in the RBBT, we use the thickness-integration procedure to derive the equations of motion of Levinson FGM beams from the dynamic equation of the plane elasticity. The complicated coupling ordinary differential equations with boundary conditions corresponding to harmonic response of the FGM beams are solved by a numerical shooting method. Meanwhile, an analytical transition between the natural frequencies of a simply supported FGM Levinson beam and those of the related homogenous Euler-Bernoulli beam are derived by ignoring the axial inertia terms. Numerical examples are presented to show validity and accuracy of the theory and the numerical approach and to examine the effects of the material gradient parameter, the length-to-depth ratio, and the boundary conditions on the free vibration response.

2 Mathematical formulation 2.1 Material distribution

Consider a functionally graded beam with a rectangular cross-section, where the length is l, the width is b, and the depth is h. The x-, y-, and z-axes are taken along the length, width, and depth of the beam, respectively, as shown in Fig. 1. The xz-plane is symmetric about the width, and the xy-plane is located in the geometrically mid-surface of the FGM beam. It is assumed that the beam is made of two different components with their material properties varying continuously in the depth direction from top to bottom surfaces. The effective material properties of the FGM beam, such as Young’s modulus E and the mass density ρ, are continuous functions and given in the following form[19, 30]:

Fig. 1 Geometry and coordinates of functionally graded beams
Figure options

where Pb denotes the material property constant at the bottom surface of the beam, and ψP (z) is a specified continuous function of coordinate z. Especially, it gives ψP (-h/2) = 1 and ψP (h/2) = Pt/Pb, where Pt denotes the material property constant at the top surface of the beam. Quantities with subscripts ‘t’ and ‘b’ represent the material constants at the top and bottom surfaces, respectively.

2.2 Equations of motion

Before the derivation of the governing equations of the FGM Levinson beam, a short review for the different beam theories is given herein. It is well known that the EBBT, or the classical beam theory, is the simplest one, in which it is assumed that the cross-section is perpendicular to the bending line so that the transverse shear deformation is neglected[1, 2, 3, 4, 5, 6, 7, 8, 9]. However, in the TBT[10, 11, 12, 13, 14, 15, 16, 17, 18, 19] or the first-order shear deformation beam theory, it allows a rotation between the cross-section and the bending line and takes into account rotational inertia effects. This rotation comes from a shear deformation which is considered by introducing a shear deformation correction factor. The TBT makes it suitable for describing the behaviour of short beams, sandwich composite beams, or beams subject to high-frequency excitation when the wavelength approaches the thickness of the beams. In the axial displacement of Timoshenko beam, only the first-order term of the coordinate in the depth direction is included. In order to consider more accurate shear deformation in the thick beams, Levinson[29] presented a new theory for beams of rectangular cross-section which included warping of the cross-sections. The displacement field contains both the first-order and third-order terms of the coordinate in the depth direction and accurately satisfies the shear-free boundary conditions at the top and bottom surfaces of the beam. It avoids the use of shear deformation correction factor as in the TBT. Another higher-order shear deformation beam theory was given by Reddy et al.[31] and Wang et al.[32]. In the RBBT, the displacement field of the beam is also assumed the same as that in the LBT[20, 21, 22, 23, 24, 25, 26, 27, 28]. However, different from the LBT in which the depth-integration procedure is used to derive the equations of motion from the dynamic equation of the plane elasticity[30], motion equations of the RBBT are derived by a variational approach, where three independent variational quantities of the deflection, the slope of the bending line, and the rotational angle of the cross-section are included in the variational formulation. As a result, in the governing equations, the higher-order bending moment and the shear force are introduced. Therefore, we are forced to additionally define a placement boundary condition on the Kirchhoff rotation, the slope of the bending line, at the clamped edges, which causes the shearing force and the higherorder shearing force to erroneously vanish at the clamped supports. Thus, the RBBT leads to an inconsistency at a clamped edge between the shearing force obtained from constitutive and equilibrium equations[33].

Therefore, the displacement field for the FGM Levinson beam is given as follows[29, 30, 31]:

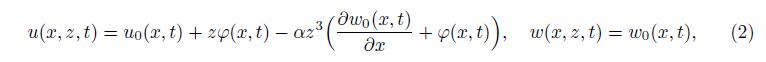
where t is the time variable, u0 and w0 are the displacements of arbitrary point at the centroidal axis in the x- and z-directions, respectively, ϕ is the rotation angle of the cross-section about the y-axis, and α = 4/(3h2). Note that by setting α = 0, Eq. (2) is reduced to the displacement field of the first-order shear deformation beam theory, or that of the TBT.

Substitution of Eq. (2) into the linear strain-displacement relation gives the strain components as follows:

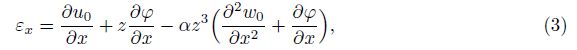
Using Hooke’s law, it yields

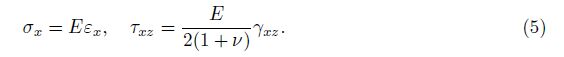
Based on the plane elasticity theory, equations of motion of the FGM beam are written by

As opposed to using the variationally-derived equations of equilibrium in the RBBT[31], Levinson[29] used the thickness-integrated equations of elasticity. By performing integration to Eqs. (6) and (7) over the cross-section of the beam and using the boundary conditionsτxz|z=±h/2 = 0, σz|z=h/2 = q, and σz|z=-h/2 = 0, it yields the following equations of the FGM Levinson beam of motion in terms of the resultant forces:

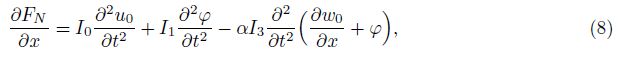
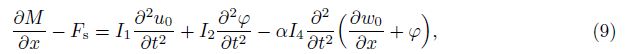
where q is the applied transverse force per length of the beam, and Ii are the resultant inertial quantities defined by

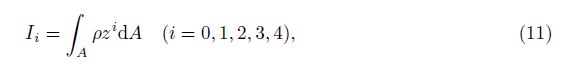
in which A is the area of cross-section. The resultant forces and the bending moment are defined as follows:

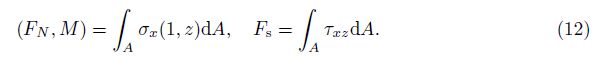
Substitution from Eqs. (3)-(5) into Eq. (12) yields the axial force FN, the shear force Fs, and the bending moment M in terms of the displacements as

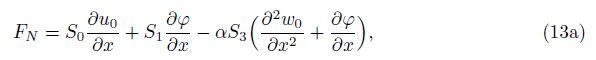
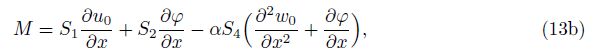
where the stiffness coefficients in Eq. (13) are calculated by the following integrals:

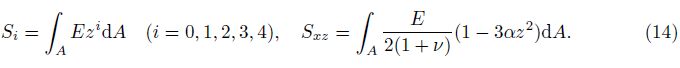
Substituting Eq. (1) into Eqs. (11) and (14), the resultant inertial quantities and the stiffness coefficients are given as follows:

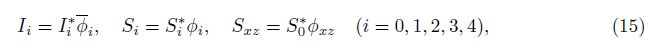
where the quantities with superscript star are related to the reference homogenous material beam, definitions of which are given in Appendix A. φi and φi are the dimensionless coefficients including the inhomogeneity and coupling of the deformation of the FGM beams. By substituting Eq. (1) into Eqs. (14) and (15), it yields the dimensionless coefficients in Eq. (15) by the following integrations:

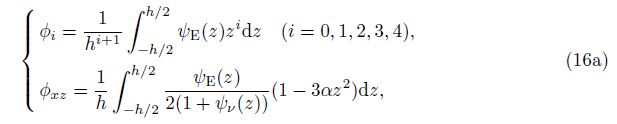
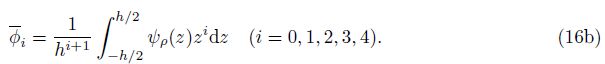
If we assume that Poisson’s ratio of the FGM beam is constant, then we have ψν(z) ≡ 1 or ν = νb = νt. For the given functions of material properties of the beam changing as the power-law functions of the coordinate z, analytical expressions of functions ψE(z), ψρ(z), and the corresponding coefficients φi, φi are given analytically in Appendix A. For the reference homogenous beam, they are given by φ0 = φ0 = 1, φ2 = φ2 = 1/12, φ1 = φ1 = φ3 = φ3 = 0, and φ4 = φ4 = 1/80.

By substituting Eq. (13) into Eqs. (8)-(10) and setting q = 0, we obtain equations of motion for free vibration of FGM Levinson beams in terms of the displacements as follows:

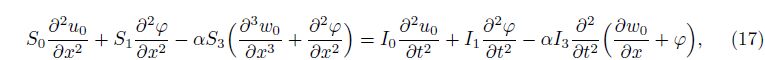
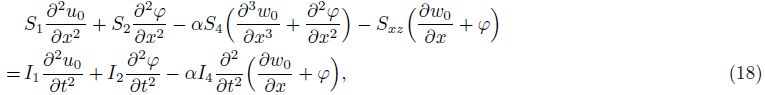
which consist of a complicated coupled system of partial differential equations with three independent unknown functions u0(x, t), w0(x, t), and ϕ(x, t).

3 Response of free vibration response of FGM Levinson beam

Free vibration response of the FGM beam can be assumed to be in a harmonic form of

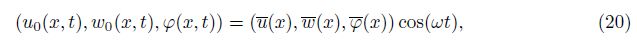
where ω is the natural frequency, and u(x), w(x), and φ(x) are the shape functions. By substituting Eq. (20) into Eqs. (17)-(19), we obtain a system of ordinary differential equations in the dimensionless forms as follows:

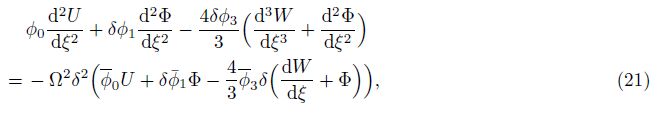
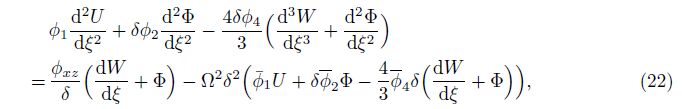
in which the dimensionless quantities are defined by

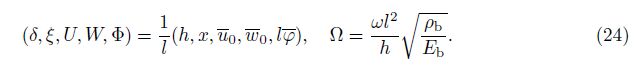
By some mathematical manipulations, the terms of the third-order derivative can be eliminated, and Eqs. (21)-(23) can be rewritten in the following forms:

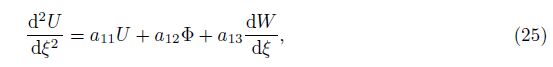
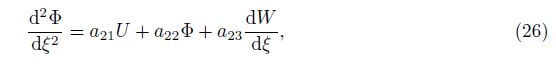
The coefficients aij in Eqs. (25)-(27) are given by

where the dimensionless parameters are defined by

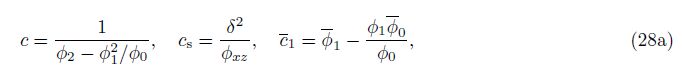
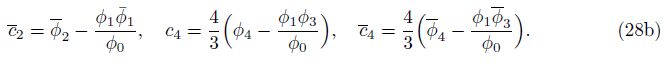
For the reference homogenous beam, we have c = 12, c2 = 1/12, c4 = c4 = 1/60, and cs = 3(1 + νb)δ2.

Equations (25)-(27) consist of a standard system of three second-order ordinary differential equations including the frequency parameter Ω in terms of the unknown shape functions of U(ξ), W(ξ), and Φ(ξ), which can be numerically solved by the shooting method[7, 19] under specified boundary conditions. In order to write dimensionless natural boundary conditions, dimensionless resultant forces and bending moment corresponding to the mode shapes are given,

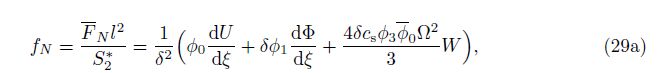
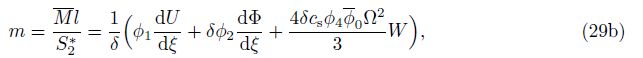
where the third terms in the brackets of Eqs. (29a) and (29b) are written by Eq. (23). From Eq. (29), we find that the inertia terms of the deflection appear in the mode shapes of the axial force and bending moment for the Levinson beams, which is different from the TBT[19].

In searching for numerical solution, three types of boundary conditions are considered.

Case 1 Clamped-clamped (C-C)

For the beam with two ends clamped, the boundary conditions can be written by

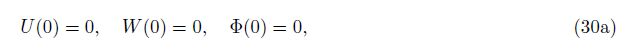
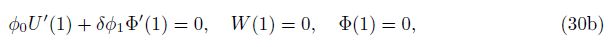
where the prime as superscript represents the derivatives respected to ξ, and the first equation in Eq. (30b) is given by fN(1) = 0 using Eq. (29a).

Case 2 Simply supported-simply supported (S-S)

The boundary conditions of the beam simply supported at the two ends are given by

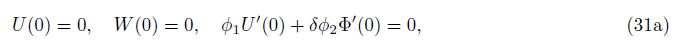
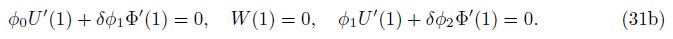
The third equations in Eqs. (31a) and (31b) are given by m(0) = m(1) = 0, and the first equation in Eq. (31b) is given by fN(1) = 0. By the condition, φ2 -φ12 /φ0 = 1/c ≠ 0, Eq. (31b) can be simplified as an uncoupled form of

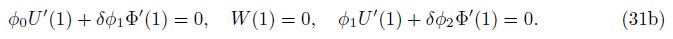
Case 3 Clamped-free (C-F)

If the beam is clamped at the left end and free at the right end, the boundary conditions are given by

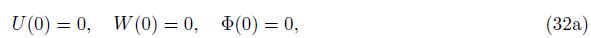
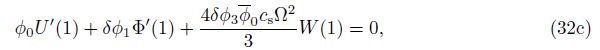
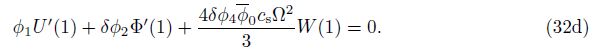
From Eqs. (32c) and (32d), we can see that the inertial terms or the frequency parameters are included in the free end boundary conditions due to the consideration of higher-order shear deformation. Obviously, the effects of the inertia terms on the vibration response are proportional quantity of δ3 = (h/l)3. Thus, for a thin beam, the effects of inertia terms can be ignored. In another respect, for the higher vibration modes (large values of Ω), the effects of the inertia terms will become significant. By setting φ3 = φ4 = 0 and using the condition φ0φ2-φ12 ≠ 0, the free end boundary conditions (32c) and (32d) are simplified to the boundary conditions, which are the same as those of the Timoshenko beams[19] as follows:

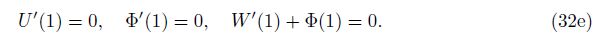
In the special case, Eqs. (25)-(27) and the associated boundary conditions for FGM Levinson beams can be easily reduced to those for FGM Timoshenko beams by letting φ3 = φ4 = φ3 = φ4 = 0 and φxz = κφ0/(2(1 + ν)), where κ is the shear deformation correction factor to be taken as 5/6 for the rectangular cross-section beam[19].

4 Approximate analytical solution for S-S beams

Through some mathematical derivations, Eqs. (20)-(22) can be written as

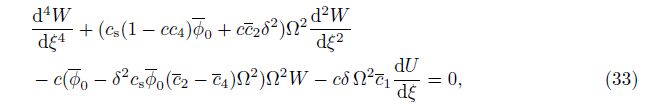
where the last term arises from the axial-transverse coupling vibrations of the FGM beams, which depends on the level of non-homogeneity of the materials in the depth direction (see the expression of parameter c1). For the homogenous beam, the term vanishes due to c1 = 0 (φ1 = φ1 = 0). From Eqs. (25) and (26), it can be found that if we ignore the inertia forces produced by the axial displacement U, the last term in Eq. (33) will not appear. Then, in the case that the axial-transverse coupling effect can be neglected, we obtain the governing equation for the free vibration of FGM Levinson beams only in terms of the dimensionless deflection shape function W as follows:

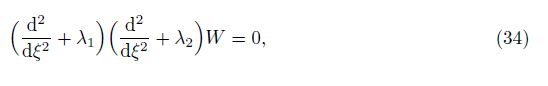
where

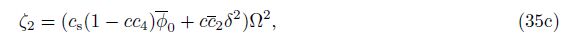
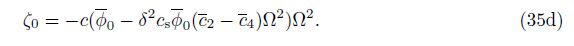
For an S-S FGM beam, if we replace the essential boundary condition in the axial direction at the left end by the natural one or change U(0) = 0 by fN(0) = 0, and in the view of Eq. (29a), we have

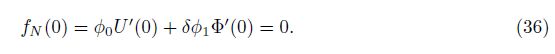
Furthermore, by the condition of φ2 - φ12 /φ0 = 1/c ≠ 0, Eq. (31a) together with Eq. (36) can be simplified as the uncoupled form of

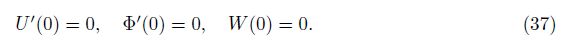
Then, by Eq. (34), the boundary conditions for an S-S FGM Levinson beam can also be written only in terms of the deflection shape function by

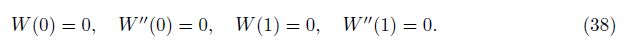
By setting δ = 0, c = 12, and φ0 = 1 in Eq. (34), one can obtain the governing equation for the homogenous Euler-Bernoulli beam as

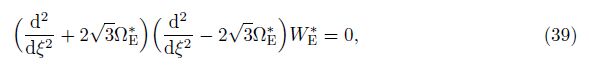
where ΩE* is the non-dimensional natural frequency of the homogenous Euler-Bernoulli beam defined by Eq. (24), and WE* is the corresponding mode shape function. Boundary conditions of the simply supported homogenous Euler-Bernoulli beam are the same as Eq. (38), which can be written by

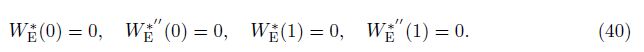
Obviously, the differential equations (34) associated the boundary conditions (38) are mathematically analogous to Eq. (39) with the boundary conditions (40). As a result, there exists a relationship between the eigenvalues of the two boundary value problems as

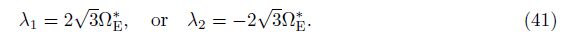
Then, by substituting Eq. (41) into Eqs. (35a) and (35b), and using Eqs. (35c) and (35d), one can finally obtain

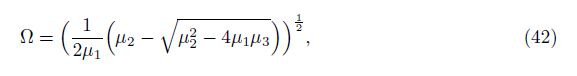
where

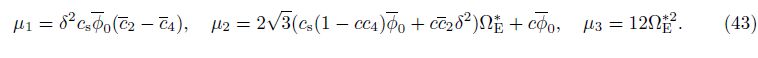
Equation (42) gives an analytical solution of natural frequency for S-S FGM Levinson beam in terms of that of the S-S homogenous Euler-Bernoulli beam, in which the parameters μ1 and μ2 are determined analytically by the coefficients φi and φi which only depend on the material properties and the geometry of the FGM beam. It is well known that , where the number m = 1, 2, 3,… is the order of the vibration mode shapes.

The relationship between the natural frequency of FGM Euler-Bernoulli beam and that of the homogenous Euler-Bernoulli beam can be derived as follows[6, 19]:

It is proved that the above relationship is independent of the boundary conditions. Therefore, Eq. (44) gives a proportional relation between the frequencies of the FGM Euler-Bernoulli beam and the reference homogenous Euler-Bernoulli beam. The proportional coefficient is determined by the parameters c and φ0 which only depend on the material gradient of the beam.

5 Numerical results and discussion

It is difficult to find any analytical solutions of Eqs. (25)-(27) associated with the boundary conditions (30)-(32) due to the complicated coupling. Herein, the shooting method is used to search for the numerical solution of the above mentioned two-point boundary value problem of the ordinary differential equations[9, 19].

In the numerical computation, the material constituents of the FGM beam are assumed to be composed by alumina (ceramic) and aluminum (metal) with the material properties as follows[22, 24, 26]:

The reference homogenous beam is considered to be made of pure aluminum. The effective material properties in the FGM beam are considered to vary as

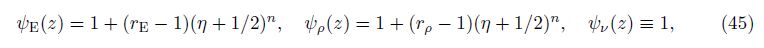
where n is the power-law exponent, η = z/h, rE = Et/Eb, and rρ = ρt/ρb. Values of the coefficients φi and φi (i = 0, 1, 2, 3, 4) for some specified values of n are listed in Table 1. It quantitatively shows the levels or the weights in the values of these parameters. It can be seen that the magnitudes of the extension-bending coupling coefficients, φ1, φ1, and the extensionshearing coupling coefficients, φ3, φ3, are more significant for FGM beams when 0.5 < n < 10.

Table 1 Values of coefficients φi and φi (i = 0, 1, 2, 3, 4) for different values of power exponent n
Table options

In Tables 2 and 3, we list the dimensionless fundamental frequencies of S-S and C-F beams with different values of the power-law exponent, n, for δ = 1/5 and δ = 1/20 based on the LBT. For the S-S beam, the present results in the first row are related to the axial boundary condition U(0) = 0, and those in the second row are related to fN(0) = 0. For the C-F beam, the values in the first row are obtained by deleting the inertia terms in the free end boundary conditions. At the same time, in order to demonstrate accuracy and validity of this study, a comparison of the present results with those based on the RBBT by S¸im¸sek[22] and Vo et al.[26] is given in the tabulations. Obviously, the present frequencies are in good agreement with those in the literature. Especially, the frequencies of the C-F beam without considering the inertial effects in the free end boundary conditions are in better agreement with those in the literature by the RBT. The increase of the value of power-law index leads to the increase of the dimensionless frequency, which is due to the fact that the increase of the value of n results in the increase of the volume fraction of the metal, in other words, in the decrease of the bending stiffness of the beam. Very small difference between the two beam theories shows that the LBT together with the numerical shooting method can predict the free vibration response of thick FGM beams with satisfactory accuracy. We also list the values of frequency based on the EBBT given by Eq. (44) in the two tables to show the shear deformation effects predicted by the shear deformational beam theories. Comparing the results of the EBBT with those of the LBT and the RBBT in the two tables, the difference between the frequencies predicted by the classical beam theory and those by the shear deformable beam theories decreases as the value of l/h increases, which means that the shear deformation effects become weaker when the beams get thinner.

Table 2 Variation of fundamental frequency Ω1 with power-law exponent n, for l/h = 5
Table options

Table 3 Variation of fundamental frequency Ω1 with power exponent n for l/h = 20
Table options

For some specified values of n and l/h, the first and second frequencies of the FGM Levinson beam with C-F ends are given in Tables 4 and 5, respectively. For a fixed value of l/h, frequencies in the first row are obtained by deleting the inertia terms in the free end boundary conditions (32c) and (32d), or under the boundary condition (32e). From the results, one can find that the effects of the inertia terms in the boundary conditions on the natural frequency depend on both the slenderness parameter, l/h, and the order of the vibration shape modes. The values of the first frequency obtained by the boundary condition (32e) are smaller than those by Eqs. (32c) and (32d). However, in Table 5, the values of the second-order frequency by Eq. (32e) are greater than those by Eqs. (32c) and (32d), which shows that the effects of the inertia terms in the boundary conditions become significant with the increase of the vibration modes and the decrease of the values of l/h. For l/h = 5 and 20, a comparison between the present results and those in Ref. [24] for the second frequency corresponding to n = 0, 1, 2, and 10 is given in Table 5. In Ref. [24], the authors considered the effect of Poisson’s ratio in the stress-strain relation. Thus, the values of √ frequencies in the literature are timed by . Obviously, the results obtained by the boundary condition (32e) are in good agreement with those in the literature. Of course, inertia terms in the free boundary conditions are not considered in the literature. Therefore, the validity of Eqs. (32c) and (32d) including frequency parameters may still need further study in the future. From the numerical results, one can found that the difference between the frequencies obtained under different boundary conditions decreases with the slenderness ration l/h due to the inertia terms proportional to δ3 = (h/l)3 (see the definition of parameter cs). When l/h = 30, the difference becomes very small, and the frequencies approach closely the frequency of the Euler-Bernoulli beam, which means that the beam is very slender and the shear deformation effect can be neglected.

Table 4 Fundamental dimensionless frequency Ω1 of C-F FGM Levinson beam versus n and l/h
Table options

Table 5 Second dimensionless frequency Ω2 of C-F FGM Levinson beam versus n and l/h
Table options

Tables 6 and 7 show the variation of the first three frequencies of S-S FGM Levinson beam with different values of the power-law exponent, n, for l/h = 5, 10, respectively. The values in the first row are obtained by the shooting method to solve Eqs. (25)-(27) under the boundary conditions (31a) and (31c). Those in the second row are obtained under the boundary conditions (38) and (31c). The results in the third row are given by the explicit solution (42). In the last row, we list the results by Thai and Vo[25] based on the RBBT for some specified values of n. It can be seen that for the homogenous beam, full ceramic (n = 0) and full metal (n = 1011), the frequencies in the first three rows obtained by different approaches are the same. It is because that the geometrically middle surface of the beam coincides with the physical neutral surface, or φ1 = φ1 = φ3 = φ3 = 0. Therefore, there is no extension-bending coupling, and the differential equations and boundary conditions are identical for the three cases. For an FGM beam, the numerical results in the second and third rows are the same. This is due to that the corresponding boundary conditions are the same, and the effect of the inertial terms of the axial displacement in the governing equations (25)-(27) and (33) is not significant due to giving up the restriction for the axial displacement, U, at the end of ξ = 0. There is a small difference between the results in the first row and those in the other two rows for the FGM beam, which arise from the difference between the boundary conditions (31a) and (37) when the material is non-homogenous. As the numerical results shown in the tabulation, Eq. (42) gives a high precision solution in the analytical form for the natural frequency of the S-S FGM Levinson beam in terms of the natural frequency of the homogenous Euler-Bernoulli beam, which is valid for arbitrary material gradient in the depth direction. Thus, the solution of a simply supported FGM Levinson beam is simplified as calculation of those parameters depending on the geometry and material gradient of the FGM beam.

Table 6 First three dimensionless frequencies of S-S FGM Levinson beam versus n for l/h = 5
Table options

Table 7 First three dimensionless frequencies of S-S FGM Levinson beam versus n for l/h = 20
Table options

Finally, in Fig. 2, a continuous variation of the first three natural frequencies versus the length-to-depth ratios of the C-C FGM Levinson beam is shown for some specified values of the exponent index n. From the results, it can be found that the effects of the slenderness ratio on the frequencies are more significant when δ < 15. When δ > 30, the frequencies tend to constants which are the frequencies of FGM Euler-Bernoulli beam. This means that for short beams, the shear deformable beam theories should be used in the analysis of the free vibration response, but for the slender beams, the classical beam theory can give a satisfied solution for the natural frequency.

Fig. 2 First three dimensionless natural frequencies versus length-to-depth ratios of C-C FGM Levinson beam for some specified values of material gradient parameter n
Figure options
6 Conclusions

The free vibration response of FGM beams is studied based on the LBT. The displacement field of the beam is given based on the third-order shear deformation theory. Motion equations for the free vibration of the non-homogenous beam are derived by directly integrating the stress-form equations of motion of plane elasticity along the beam depth with the higherorder shear deformation and the axial, transversal, rotational, and the tension-bending coupling inertia forces included by assuming the material properties of the beam to be varied arbitrarily in the thickness direction. By a shooting method to solve the boundary value problem of the three coupled ordinary differential equations (25)-(27) with different boundary conditions, the free vibration response of the FGM Levinson beam is obtained numerically. The effects of the material gradient parameter, the length-to-depth ratio, and the boundary conditions on the frequency are examined quantitatively through the numerical results. Comparisons of the presented numerical solutions with those in the literature are given to show validity and efficiency of the theory and methodology dealing with the free vibration of FGM Levinson beam.

Based on the LBT, natural boundary conditions at the free end are derived in terms of the mode shape functions, in which the terms of the inertia force or of the natural frequency are included. This arises from the terms of the higher-order shear deformation in the assumed displacement filed which will appear in the axial resultant force and bending moment. It is the first attempt in this presentation, to the best of the authors’ knowledge, to consider the effect of inertial forces in the free end boundary conditions for the C-F FGM beams based on the higher-order shear deformation beam theory. Numerical results show that this effect is more significant for the thick FGM beam.

For the S-S FGM Levinson beam, a closed form solution for natural frequency is derived by ignoring the axial-transverse coupling effect produced by the axial displacement. This solution is expressed explicitly in terms of the natural frequency of the related homogenous Euler-Bernoulli beam and the dimensionless coefficients determined by the geometry and material gradient distribution in the depth of the beam. Numerical results show that this solution gives a very accurate prediction for the frequencies of a simply supported FGM Levinson beam.

Appendix A

The resultant stiffness and inertia coefficients of the reference homogenous beams are given by

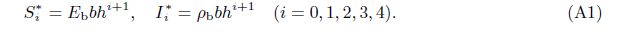
If the material properties of the FGM beam are assumed to vary continuously through the depth of the beam by a power-law functions, then the functions in Eq. (1) can be given by Eq. (45). Substituting Eq. (45) into Eq. (16) yields the dimensionless coefficients φi analytically as follows:

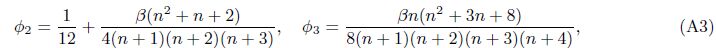
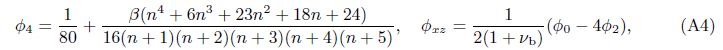
in which β = rE - 1. By replacing β with β = rρ - 1 in Eqs. (A2)-(A4), one can obtain the similar analytical expressions for coefficients φi by changing β to β.

References
[1] Alshorbagy, A. E., Eltaher, M. A., and Mahmoud, F. F. Free vibration characteristics of a functionally graded beam by finite element. Applied Mathematics Modeling, 35, 412-425(2011)
[2] Şimşek, M. and Kocatürk, T. Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Composite Structures, 90, 465-473(2009)
[3] Khalili, S. M. R., Jafari, A. A., and Eftekhari, S. A. A mixed Ritz-DQ method for forced vibration of functionally graded beams carrying moving loads. Composite Structures, 92, 2497-2511(2010)
[4] Pradhan, S. C. and Murmu, T. Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundation using differential quadrature method. Journal of Sound and Vibration, 321, 342-362(2009)
[5] Yang, J. and Chen, Y. Free vibration and buckling analysis of functionally graded beams with edge cracks. Composite Structures, 93, 48-60(2011)
[6] Li, S. R. and Liu, P. Analogous transformation of static and dynamic solutions between functionally graded material and uniform beams (in Chinese). Mechanics and Engineering, 32, 45-49(2010)
[7] Li, S. R., Su, H. D., and Cheng, C. J. Free vibration of functionally graded material beams with surface-bonded piezoelectric layers in thermal environment. Applied Mathematics and Mechanics (English Edition), 30(8), 969-982(2009) DOI 10.1007/s10483-009-0803-7
[8] Huang, Y. and Li, X. F. A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. Journal of Sound and Vibration, 329, 2291-2303(2010)
[9] Liu, Y. and Shu, D. W. Free vibration analysis of exponential functionally graded beams with a single delamination. Composites:Part B, 59, 166-172(2014)
[10] Sina, S. A., Navazi, H. M., and Haddadpour, H. An analytical method for free vibration analysis of functionally graded beams. Materials and Design, 30, 741-747(2009)
[11] Li, X. F. A unified approach for analyzing static and dynamic behaviours of functionally graded Timoshenko and Euler-Bernoulli beams. Journal of Sound and Vibration, 318, 1210-1229(2008)
[12] Pradhan, K. K. and Chakraverty, S. Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method. Composites:Part B, 51, 175-184(2013)
[13] Xiang, H. J. and Yang, J. Free and forced vibration of laminated FGM Timoshenko beam of variable thickness under heat conduction. Composites:Part B, 39, 292-303(2008)
[14] Shahba, M., Attarnejad, R., Tavanaie Marvi, M., and Hajilar, M, S. Free vibration and stability analysis axially functionally graded tapered Timoshenko beams with classical and non-classical boundary conditions. Composites:Part B, 42, 801-808(2011)
[15] Huang, Y., Yang, L. E., and Luo, Q. A. Free vibration of axially graded Timoshenko beams with non-uniform cross-section. Composites:Part B, 44, 1493-1498(2013)
[16] Nguyen, T. K., Vo, T. P., and Thai, H. T. Static and free vibration of axially loaded functionally graded beams based on the first-order-shear deformation theory. Composites:Part B, 55, 147-157(2013)
[17] Rajasekaran, S. and Tochaei, E. N. Free vibration analysis of axially functionally graded tapered Timoshenko beams using differential transformation element method and differential quadrature element method of lowest-order. Meccanica, 49, 995-1009(2014)
[18] Li, S. R. and Fan, L. L. Free vibration of FGM Timoshenko beams with through-width delamination. Science China Physics, Mechanics and Astronomy, 57, 927-934(2014)
[19] Li, S. R., Wan, Z. Q., and Zhang, J. H. Free vibration of functionally graded beams based on both classical and the first-order shear deformation beam theories. Applied Mathematics and Mechanics (English Edition), 35(5), 591-606(2014) DOI 10.1007/s10483-014-1815-6
[20] Aydogdu, M. and Taskin, V. Free vibration analysis of functionally graded beams with simply supported edges. Material Design, 28, 1651-1656(2007)
[21] Şimşek, M. Vibration analysis of a functionally graded beam under moving mass by using different beam theories. Composite Structure, 92, 904-917(2010)
[22] Şimşek, M. Fundamental frequency analysis of functionally graded beams by using different higherorder beam theories. Nuclear Engineering and Design, 240, 697-705(2010)
[23] Mahi, A., Adda-Bedia, E. A., Tounsi, A., and Mechab, I. An analytical method for temperaturedependent free vibration analysis of functionally graded beams with general boundary conditions. Composite Structure, 92, 1877-1887(2010)
[24] Pradhan, K. K. and Chakraverty, S. Effects of different shear deformation theories on free vibration of functionally graded beams. International Journal of Mechanical Science, 82, 149-160(2014)
[25] Thai, H. T. and Vo, T. P. Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories. International Journal of Mechanical Sciences, 62, 57-66(2012)
[26] Vo, T. P., Thai, H. T., Nguyen, T. K., and Inam, F. Static and vibration analysis of functionally graded beams using refined shear deformation theory. Meccanica, 49, 155-168(2014)
[27] Vo, T. P., Thai, H. T., Nguyen, T. K., Maheri, A., and Lee, J. Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Engineering Structures, 64, 12-22(2014)
[28] Shen, H. S. and Wang, Z. X. Nonlinear analysis of shear deformable FGM beams resting on elastic foundations in thermal environments. International Journal of Mechanical Sciences, 89, 195-206(2014)
[29] Levinson, M. A new rectangular beam theory. Journal of Sound and Vibration, 74, 81-87(1981)
[30] Li, S. R., Wan, Z. Q., and Wang, X. Homogenized and classical expressions for static bending solutions for functionally graded material Levinson beams. Applied Mathematics and Mechanics (English Edition), 36(7), 895-910(2015) DOI 10.1007/s10483-015-1956-9
[31] Reddy, J. N., Wang, C. M., and Lee, K. H. Relationships between bending solutions of classical and shear deformation beam theories. International Journal of Solids and Structures, 34, 3373-3384(1997)
[32] Wang, C. M., Reddy, J. N., and Lee, K. H. Shear Deformable Beams and Plates-Relationship with Classical Solutions, Elsevier, Oxford (2000)
[33] Groh, R. M. J. and Weaver, P. M. Static inconsistencies in certain axiomatic higher-order shear deformation theories for beams, plates and shells. Composite Structures, 120, 231-235(2015)