Shanghai University
Article Information
- D. V. DUNG, L. K. HOA, B. T. THUYET, N. T. NGA. 2016.
- Buckling analysis of functionally graded material (FGM) sandwich truncated conical shells reinforced by FGM stiffeners filled inside by elastic foundations
- Appl. Math. Mech. -Engl. Ed., 37(7): 879-902
- http://dx.doi.org/10.1007/s10483-016-2097-9
Article History
- Received 2015-11-20;
- in final form 2016-03-08
2. Faculty of Basic Science, Military Logistic Academy, Hanoi 120160704, Vietnam;
3. Faculty of Mining, Hanoi University of Mining and Geology, Hanoi 120160704, Vietnam
Truncated conical shells are used in various engineering applications such as hoppers, marine and ocean engineering structures, components of missiles and spacecrafts, and other civil applications.
The buckling and vibration analysis of plates and shells containing conical shells subjected to external loads is one of the fundamental important problems attracting considerable attention of many researchers. There are many results presented in the well-known monographs[1, 2, 3, 4, 5] and in the literature[6, 7, 8, 9, 10, 11, 12, 13, 14, 15].
In recent years, because functionally graded material (FGM) structures have been widely used in modern engineering, the stability and vibration behaviors of FGM plates and shells have attracted increasing research effort. Among those available, the results of Shen were presented in his monograph[5]. Sofiyev[16, 17] investigated the linear stability and vibration of unstiffened FGM truncated conical shells with different boundary conditions. Sofigev[18] also presented the nonlinear buckling behavior and nonlinear vibration[19] of FGM truncated conical shells, and considered the buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler-Pasternak foundations[20]. For linear analysis, the general characteristic in his works is that the modified Donnell-type equations were used, and the Galerkin method was applied to obtain the closed-form relations of bifurcation type buckling load or to find expressions of fundamental frequencies, whereas for nonlinear analysis, the large deflection theory with von Karman-Donnell-type of kinetic nonlinearity was used.
Based on the first-order shell deformation theory (FSDT) by Love-Kirchhoff and the Sanders nonlinear kinetic equations, the thermal and mechanical instability of FGM truncated conical shells was also investigated by Naj et al.[21]. The results on the buckling of un-stiffened FGM conical panels under mechanical loads were presented by Bich et al.[22], in which the linearized stability equations in terms of displacement components were derived by the classical shell theory. The Galerkin method was applied to obtain the explicit expression of buckling load. Malekzadeh and Heydarpour[23] studied the influence of centrifugal and Coriolis forces in combination with other geometrical and material parameters on the free vibration behavior of rotating FGM truncated conical shells subjected to different boundary conditions based on the FSDT.
It is well known that the shells, in which the inner and outer surfaces are covered, belong to the class of sandwich structures. Covered shells are widely used as structural elements in modern equipment, aircraft, shipbuilding, nuclear reactors, and aerospace. There are significant studies on the stability and vibration of layered FGM shells. Liew et al.[24] analyzed the nonlinear vibration of a three-layer coating-FGM-substrate based on the FSDT with the geometric nonlinearity in von Karman sense. Alibeigloo and Liew[25] investigated the free vibration of sandwich cylindrical panel with FGM core using the three-dimensional theory of elasticity. The state space technique was used to obtain natural frequencies analytically in this work. Li and Batra[26] considered the buckling of a simply supported three-layer circular cylindrical shell under the axial compressive load. The inner and outer layers of the shell are comprised of the same homogenous and isotropic material, and the middle layer is made of FGM. Sofiyev and Kuruoglu[27] solved the problem on vibration and buckling of the cylindrical shell with FGM coatings in an elastic medium. By the Galerkin method, the dimensionless torsional buckling load and the dimensionless torsional frequency parameter of shell were obtained analytically. Sofiyev[28] studied the vibration and buckling of sandwich cylindrical shells covered by different types of coatings, such as functionally graded, metal, and ceramic coatings and subjected to a uniform hydrostatic pressure using the FSDT. The closed-form solutions for non-dimensional frequencies and critical hydrostatic pressures were obtained. Najafov et al.[29] considered the linear and nonlinear vibrations of a truncated conical shell. Both internal and external surfaces are covered by functionally graded coatings. The theoretical formulation was based on the von Karman-Donnell-type nonlinear kinematics. The basic equations were reduced to the ordinary differential equations depending on time with geometric nonlinearity using the superposition and Galerkin methods. By applying the homotopy perturbation method to the foregoing equation, the relation between the nonlinear frequency parameters with the dimensionless amplitude of a truncated conical shell with functionally graded coatings was obtained. For conical shells, the stability of a thin three-layered composite truncated conical containing an FGM layer subjected to a non-uniform lateral pressure was studied by Sofiyev et al.[30], the nonlinear stability of a truncated conical shell with FGM coatings in the finite deflection was considered by Deniz[31], and the dynamic buckling analysis of a truncated conical shell with FGM coatings under a time dependent axial load in the large deformation was presented by Sofiyev[32].
It can be seen that the above introduced works only relate to unstiffened structures. However, in practice, plates and shells including conical shells are usually reinforced by stiffeners system to provide the benefit of added load carrying capability with a relatively small additional weight. Thus, the study on static and dynamic behaviors of these structures is significant. Weingarten[33] conducted a free vibration analysis for a ring-stiffened simply supported conical shell by considering an equivalent orthotropic shell and using the Galerkin method. He also carried out experimental investigations. Crenwelge and Muster[34] applied an energy approach to find the resonant frequencies of simply supported ring-stiffened and ring and stringer-stiffened conical shells. Mustaffa and Ali[35] studied the free vibration characteristics of stiffened cylindrical and conical shells by structural symmetry techniques. Srinivasan and Krishnan[36] obtained the results on the dynamic response analysis of stiffened conical shell panels, in which the effect of eccentricity was taken into account. The integral equations for the space domain and mode superposition for the time domain were used in their work. Based on the Donnell-Mushtari thin shell theory and the stiffeners smeared technique, Mecitoglu[37] studied the vibration characteristics of a stiffened truncated conical shell by the collocation method. The minimum weight design of axially loaded simply supported stiffened conical shells with natural frequency constraints was considered by Rao and Reddy[38]. The influence of place of the stiffeners inside as well as outside on the optimum design of the conical shell was studied. The expressions for the critical axial buckling load and the natural frequency of vibration of conical shell were also derived.
For eccentrically stiffened FGM (ES-FGM) structures, there are some important investigations which have focused on the analysis of static buckling, post-buckling, vibration, and dynamic buckling of plates and shells. By FGM stiffeners, Najafizadeh et al.[39] studied buckling of FGM cylindrical shell reinforced by rings and stringers under axial compression with the linearized stability equations in terms of displacements. The stiffeners and skin, in their work, were assumed to be made of FGMs, and their properties vary continuously through the thickness direction. Following this direction, Dung and Hoa[40, 41] obtained the results on the static nonlinear buckling and post-buckling analysis of eccentrically stiffened FGM circular cylindrical shells under the external pressure and the torsional load. The material properties of shell and stiffeners were assumed to be continuously graded in the thickness direction. The deflection function was chosen by three-term. The Galerkin method was used to obtain the closed-form expressions to determine critical buckling loads. By homogenous stiffeners, Bich et al.[42, 43] obtained the results on the nonlinear dynamic analysis of eccentrically stiffened FGM cylindrical panels and imperfect doubly curved thin shallow shells. The governing equations of motion were derived by the smeared stiffeners technique and the classical shell theory with von Karman geometrical nonlinearity. With the deflection function chosen by three-term, Dung and Nam[44] studied the nonlinear dynamic behavior of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium by semi-analytical approach.
The review of the literature signifies that up to now, for eccentrically stiffened conical shells, the analytical studies are still very limited. Principal cause is the inherent complexity of governing equations of conical shell. Those are variable coefficient partial differential equations. In addition, for a stiffened conical shell, the spacing between stringers in the meridional direction also varies. Recently, Dung et al.[45] investigated the buckling of combined loaded stiffened FGM truncated conical shells without elastic foundations. The closed-form expressions to determine critical buckling loads were obtained.
Unlike the studies in Refs. [44] and [45], in which the system of stiffeners is homogeneous and the material properties vary with a power law, in this paper, the system of stiffeners is FGM and the material properties are graded with the general sigmoid law. An analytical solution for buckling of eccentrically stiffened sandwich truncated conical shell consisting of two FGM coating layers and one core layer being metal or ceramic subjected to an axial compressive load and an external uniform pressure resting on elastic foundations is developed. Shells are reinforced by stringers and rings, in which the material properties of shell and stiffeners are graded in the thickness direction with a general model of sigmoid law distribution. The shell-foundation interaction is described by the two-parameter elastic foundation model or the Pasternak foundation model. Two models of coated shell-stiffener arrangement are investigated. The change of spacing between stringers in the meridional direction is taken into account. The stability equations for stiffened shells are derived based on the Donnell shell theory and the smeared stiffeners technique. The resulting equations, which are the couple set of three-variable-coefficient partial differential equations in terms of displacement components, are solved by the Galerkin method. The closed-form expression for determining the buckling load is obtained. The influence of various parameters such as the core layer, the coating layer, the stiffener, the foundation, the dimensional parameters, and the volume fraction index of materials on the stability of shell is discussed. The accuracy of the present study is validated by comparing with available result in related literature.
2 ES-FGM sandwich shell model and elastic foundationsConsider an ES-FGM sandwich truncated conical shell consisting of two FGM coating layers and one core layer being metal or ceramic. The geometry of shell is shown in Fig. 1, where h is the total thickness, α is the semi-vertex angle, L is the length, and R is the small base radius of shell. The truncated conical shell is referred to a curvilinear coordinate system (x, θ, z), in which x is in the generatrix direction measured from the vertex of conical shell, θ is in the circumferential direction, and z is in the direction of the outwards normal of the middle surface. x0 indicates the distance from the vertex to the small base of the shell. Assume that the shell is reinforced by the closely spaced FGM stiffener system, and two models following are investigated. In addition, it is assumed that the conical shell is made of FGMs varying continuously through the shell thickness direction with the power distribution law. Two models with four cases are investigated in this paper.

|
| Fig. 1 Geometry and cross-section of ES-FGM sandwich truncated conical shell, where 1 denotes FG layer, 2 denotes core layer, and 3 denotes FG layer |
First model
Case 1 FGM-metal core-FGM conical shell and outside FGM stiffener
Case 2 FGM-metal core-FGM conical shell and inside FGM stiffener
Second model
Case 3 FGM-ceramic core-FGM conical shell and outside FGM stiffener
Case 4 FGM-ceramic core-FGM conical shell and inside FGM stiffener
In Case 1, Young’s modulus of shell is expressed by
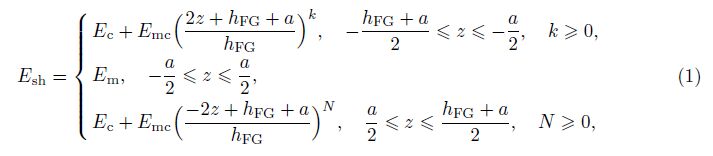
and for FGM stiffeners,
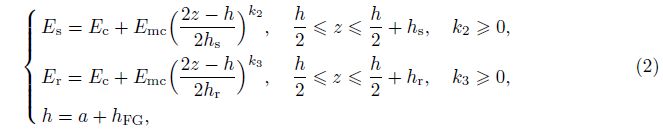
where hFG/2 is the thickness of each FGM coating layer, a is the thickness of the middle layer, and hs and hr are the thicknesses of the stringer and the ring, respectively,

k, N, k2, and k3 are the volume fractions indices of shell, stringer, and ring, respectively, and c, m, sh, s, and r are the subscripts denoting ceramic, metal, shell, stringers, and ring, respectively. Ec and Em are Young’s moduli of the ceramic and metal, respectively. Esh, Es, and Er are Young’s moduli of shell, stringer, and ring, respectively. Poison’s ratios are assumed constant, νsh = νs = νr = ν =constant.
From Eqs. (1) and (2), it is evident that a continuity between the layers of shell and between shell and stiffeners is satisfied.
It can be seen that Eq. (1) is the general equation, from which we can obtain particular cases as the FGM shell with the sigmoid distribution law (a = 0, k = N), the FGM shell with the a-layer one coated by FGM-layer (k = 0 or N = 0), the full metal shell (k = 0, N = 0), and full ceramic shell (k = ∞, N = ∞).
Young’s moduli for remaining cases are given in Appendix A.
The shell-foundation interaction is described by the two-parameter elastic foundation model or the Pasternak foundation model as
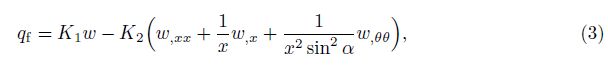
where w is a deflection of the truncated conical shell, K1 (N/m3) is the Winkler foundation modulus, and K2 (N/m) is the shear layer foundation stiffness of the Pasternak model.
3 Fundamental relations and nonlinear equilibrium equationsAccording to the Donnell shell theory with the von Karman geometrical nonlinearity, the strain components at the distance z from the middle surface of shell are in the forms of[2]
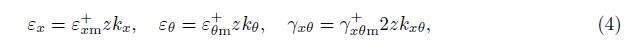
where εxmand εθm are the normal strains, γxθm is the shear strain at the middle surface of the shell, and kx, kθ, and kxθ are the change of curvatures and twist, respectively. They are relate to the displacement components as[2]
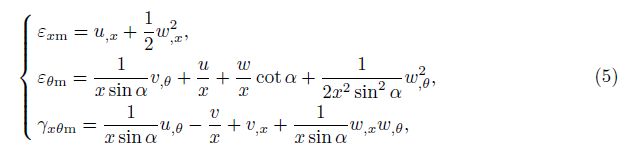
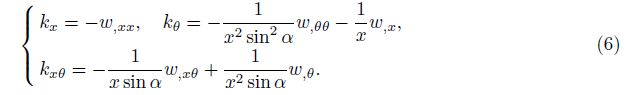
The stress-strain relations for the FGM sandwich conical shell are given by
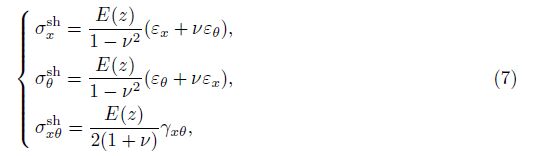
and for FGM stiffeners,

where the superscripts sh and s denote shell and stiffeners, respectively. Es and Er are Young’s moduli of stiffener in the x-direction and the θ-direction, respectively. To guarantee the continuity between the stiffener and shell, the stiffener is taken to be pure-metal if it is located at the metal-rich side and is pure-ceramic if it is located at the ceramic-rich side.
The force and moment resultants taking into account the contribution of stiffeners are
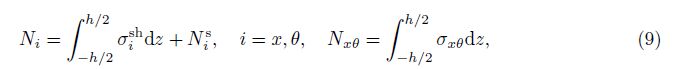
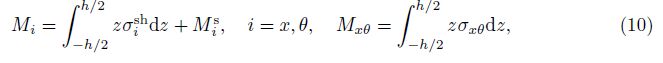
where Nis and Mis (i = x, θ) are the force and moment resultants of stiffeners, respectively.
Substituting Eq. (7) into Eqs. (9)-(10), using the smeared stiffener technique, and taking into account the change of spacing between stringers in the meridional direction, we obtain[38, 45]
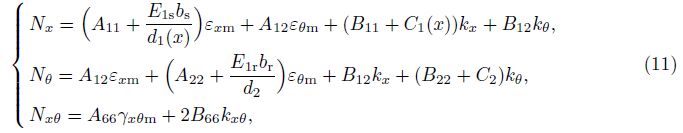
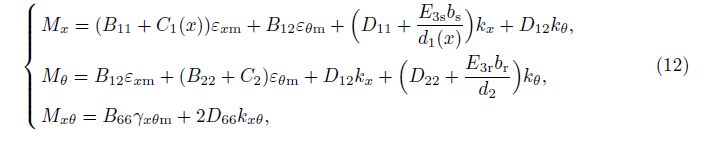
where the coefficients can be defined as follows.
In Case 1,

in which ns and nr are the numbers of stringer and ring, respectively, and bs and br are the width of stringer and the width of ring, respectively. Also, d1 = d1(x) and d2 are the distances between two stringers and two rings, respectively (see Fig. 2).

|
| Fig. 2 Geometry of stiffeners and foundation |
The coefficients for remaining cases are given in Appendix A.
According to the Donnell shell theory, the nonlinear equilibrium equations of truncated conical shells taking into account the elastic foundation are in the forms of[2]
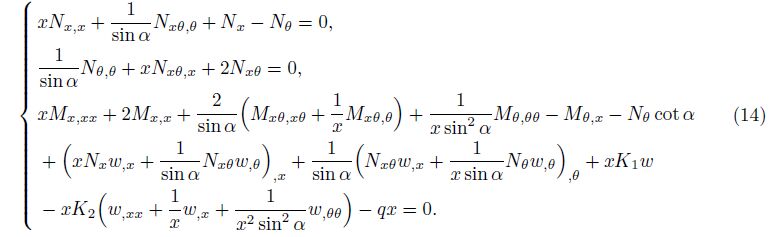
Assume that a shell is subjected to the compressive load of intensity

parallel to the axisymmetric axis of the shell at x = x0 and the external uniform pressure q (Pa). Thus, according to the symmetry of geometry and loading conditions, the prebuckling force resultants of shell are found from the equilibrium equation (14) as
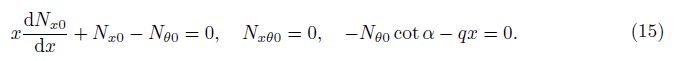
Solve this system with the condition at x = x0 as
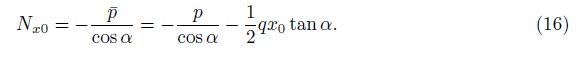
Then, we obtain
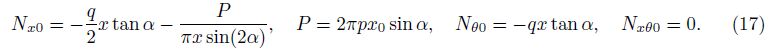
The linearization stability equations of conical shell are derived using the adjacent equilibrium criterion[2]. Assume that the equilibrium state of the ES-FGM conical shell under mechanical loads is defined in terms of the displacement components u0, v0, and w0. We give arbitrarily small increase u1, v1, and w1 to the displacement variables. Therefore, the total displacement components of a neighboring state are
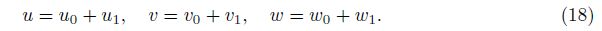
Similarly, the force and moment resultants of a neighboring state may be related to the state of equilibrium as
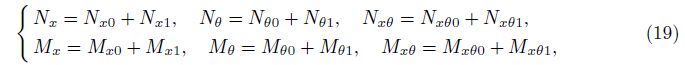
where the terms with subscript 0 correspond to the displacements u0, v0, and w0, and those with subscript 1 represent the portions of increments of force and moment resultants that are linear in u1, v1, and w1. The linearization stability equations may be obtained by substituting Eqs. (18) and (19) into Eq. (14), and note that the terms in the resulting equations with subscript 0 satisfy the equilibrium equations and therefore drop out of the equations. In addition, the nonlinear terms with subscript 1 are ignored because they are small compared with the linear terms. The remaining terms form the stability equations as follows:

where the force and moment resultants for the state of stability are given by
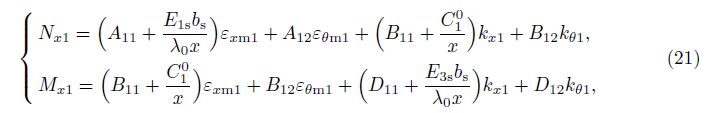
and the linear forms of the strains and the change of curvatures in terms of the displacement components are
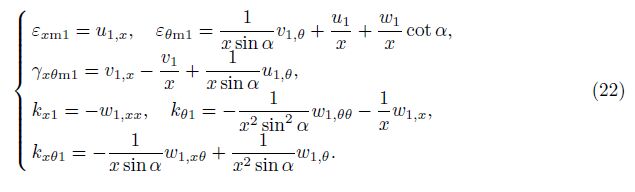
Substituting Eqs. (17), (21), and (22) into Eq. (18), the stability equations in terms of the buckling displacements are in the forms of
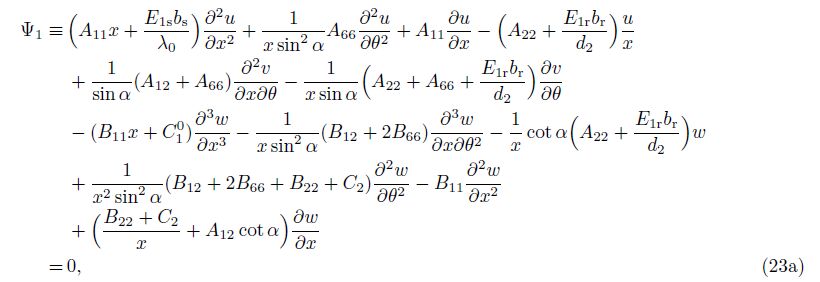
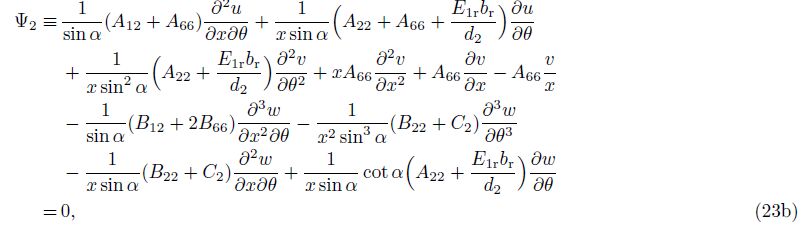
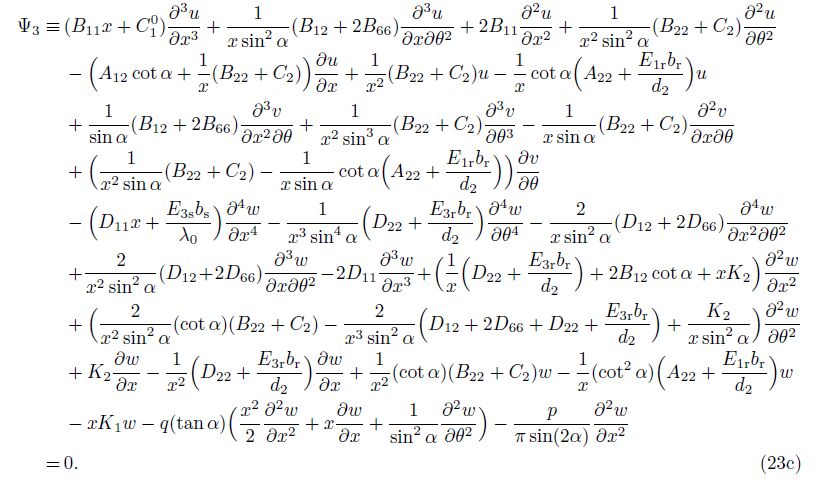
The system of Eq. (23) is used to analyze stability and find the critical buckling load of ES-FGM coated truncated conical shells. It is difficult because these equations are a couple set of three-variable-coefficient partial differential equations. This problem will be solved below.
6 Buckling analysisAssume that a shell is simply supported at both ends. Thus, the boundary conditions are expressed by
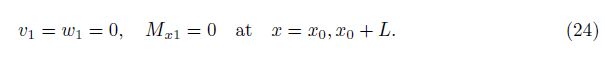
The approximate solution satisfying the boundary conditions of Eq. (24) is in the form of[45]
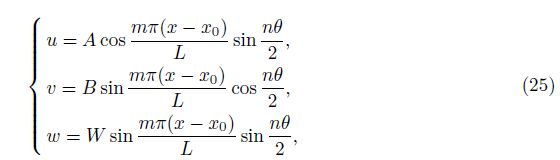
where A, B, and W are the amplitudes of the buckling displacements, m is the number of half-waves along a generatrix, and n is the number of full-waves along a parallel circle. For the sake of convenience in integration, Eqs. (23a) and (23b) are multiplied by x and Eq. (23c) by x2, and applying the Galerkin method for the resulting equations yields
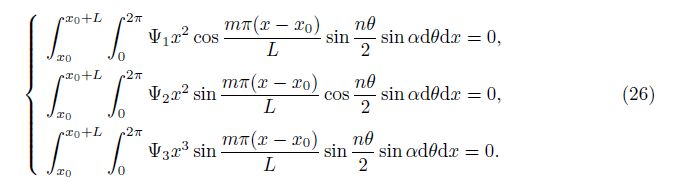
Substituting the expression (25) into Eq. (26), after integrating longer and some rearrangements, Eq. (26) may be written in the following form:
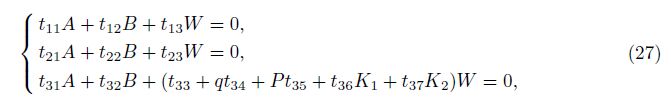
where the coefficients tij are defined in Appendix B.
Because the solutions of Eq. (27) are nontrivial, the determinant of coefficient matrix of this system must be zero. Developing that determinant and solving the resulting equation for combination of P and q, we obtain
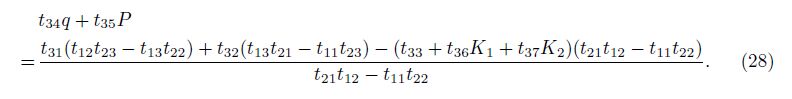
The explicit equation (28) is used to determine the critical buckling load of ES-FGM coated conical shells surrounded by elastic foundation and under axial compressive load and uniform pressure load. The buckling loads P and q still depend on the values of m and n. Therefore, minimizing these expressions with respect to m and n, we obtain the critical values of P and q, respectively.
7 Numerical results and discussion 7.1 Validation of present approachTo validate the present study, Fig. 3 compares the present results for an un-stiffened isotropic truncated conical shell under an external pressure with the results given in the monograph of Brush and Almroth[2]. The data base in this case is taken as a = 0, k = 0, h = 0.01m, R = 100h, ν = 0.3, P = 0, and q* = 104Rqcr/(Eh), where qcr is found from Eq. (28).

|
| Fig. 3 Comparisons with results of Brush and Almroth[2] for un-stiffened isotropic conical shells (P = 0) |
Figure 4 compares the present results with those of Seide[6] and Sofiyev[20] for a pure isotropic
un-stiffened truncated conical shell without foundation. The input parameters are a = 0,  , and
, and  [6, 20], where Pcr is found from Eq. (28).
[6, 20], where Pcr is found from Eq. (28).
Table 1 compares the present results with those of Baruch et al.[8] and Naj et al.[21] for a
pure isotropic un-stiffened truncated conical shell. The input parameters are a = 0, k = 0,
h = 0.01m, R = 100h, ν = 0.3, q = 0, and P* = Pcr/Pcl with  in Ref. [21],
where Pcr is found from Eq. (28).
in Ref. [21],
where Pcr is found from Eq. (28).
It can be seen that good agreement is obtained in these three comparisons.
7.2 Effect of core layer aIn the following subsections, the materials used are alumina with Ec = 380GPa and aluminum with Em = 70GPa and ν = 0.3. The geometrical parameters are taken as h = 0.005m, R/h = 150, L = 2R, hs = hr = 0.003m, and bs = br = 0.002m.
The effects of the thickness of core to FGM coating layer ratio a/hFG on the critical buckling loads qcr and Pcr of ES-FGM coated truncated conical shell are shown in Tables 2 and 3, respectively. It is observed that when a/hFG increases, qcr and Pcr both increase markedly in Cases 3 and 4, but they decrease in Cases 1 and 2. For example, in Table 3, for Case 1, comparing Pcr = 16.127 68 MN (when a/hFG = 0.5 and q = 0kPa) with Pcr = 11.745 86 MN (when a/hFG = 2, q = 0 kPa), it is observed that the critical load decreases about 27%. The effects of a/hFG ratio are also illustrated in Figs. 5 and 6. Once again, they are also shown that the critical buckling increases when a/hFG increases in Cases 3 and 4, and inversely in Cases 1 and 2. This result agrees with the actual property of material. As the core layer a (for Cases 3 and 4) increases, the volume fraction of ceramic increases, and the value of the critical load is larger. Inversely, when the core layer a (for Cases 1 and 2) increases, the volume fraction of metal increases, and the value of critical load is smaller.
 |
 |

|
| Fig. 5 Effects of a/hFG on buckling load qcr (P = 0 and k2 = k3 = N = k = 1) |

|
| Fig. 6 Effects of a/hFG on critical load Pcr (q = 0 and k2 = k3 = N = k = 1) |
Tables 4 and 5 present the effect of the semi-vertex angle α on the critical pressures qcr and the critical axial compressive load Pcr, respectively. It can be seen that the critical buckling load of the truncated conical shell strongly decreases when the semi-vertex angle increases. For example, in Table 4, for Case 1, with P = 0 MN, when the semi-vertex angle varies from 10° to 70°, the critical pressure qcr decreases from 1 561.046 85 kPa to 161.134 28 kPa. This remark has also been pointed out in Ref. [45]. Graphically, the effects of the semi-vertex angle α on the critical axial compressive load Pcr and the critical pressure qcr are plotted in Figs. 7 and 8, respectively. They also show that the critical axial compressive load Pcr and the critical pressure qcr decrease when α increases.
 |
 |

|
| Fig. 7 Effects of α on critical pressure qcr (k2 = k3 = N = k = 1) |

|
| Fig. 8 Effects of α on critical load Pcr (q = 0 and k2 = k3 = N = k = 1) |
The effects of the radius-to-thickness ratio R/h and the length-to-radius ratio L/R on the critical buckling loads qcr and Pcr of ES-FGM are presented in Tables 6 and 7, respectively.
 |
 |
It can be seen that the critical buckling load decreases markedly when R/h and L/R increase. This result agrees with the actual property of structure, i.e., when the shell is thinner or longer, the value of critical load is smaller. For example, in Table 6, for Case 1, comparing qcr = 623.177 54kPa (with L/R = 1.5, R/h = 100) with qcr = 437.458 68kPa (with L/R = 2, R/h = 100), the critical load decreases about 30%. This point is also illustrated in Figs. 9 and 10 for the effect of R/h and Figs. 11 and 12 for the effect of L/R. Thus, the critical buckling load is very sensitive with the change of R/h or L/R.

|
| Fig. 9 Effects of R/h on critical pressure qcr (Case 2, P = 0, k2 = k3 = N = k = 1) |

|
| Fig. 10 Effects of R/h on critical load Pcr (Case 2, q=0, k2=k3 =N =k=1) |

|
| Fig. 11 Effects of L/R on critical pressure qcr (Case 2, P = 0, k2 = k3 = N = k = 1) |

|
| Fig. 12 Effects of L/R on critical load Pcr (Case 2, q = 0, k2 = k3 = N = k = 1) |
The effects of the indices k, N, k2, and k3 on the critical buckling loads are given in Figs. 13 and 14. In Figs. 13 and 14, the lines 1 and 2 correspond to Case 2 with a/hFG = 0 and a/hFG = 2, respectively. The lines 3 and 4 correspond to Case 4. It can be observed that for Case 2 (lines 1 and 2), when k increases, the critical loads qcr and Pcr increase. This is reasonable because the ceramic quantity in the shell increases (see Eq. (1)). Conversely, for Case 4 (lines 3 and 4), when k increases, the critical loads qcr and Pcr decrease because the ceramic quantity in the shell decreases (see Appendix A). The numerical results on the effects of k, N, k2, and k3 on the critical buckling loads are presented in Tables 8 and 9. It can be seen that these effects are significant. For example, in Table 9, for Case 1, comparing Pcr = 15.347 04MN (N = k = 1, k2 = k3 = 1/N) with Pcr = 20.300 84MN (N = k = 5, k2 = k3 = 1/N), we can see that the critical load increases about 24%. For Case 2, comparing Pcr = 15.017 76MN (N = k = 1, k2 = k3 = k) with Pcr = 20.263 29 MN (N = k = 5, k2 = k3 = k), the critical load increases about 25.87%. For Case 3, comparing Pcr = 17.981 57MN (N = k = 1, k2 = k3 = N) with Pcr = 12.689 01MN (N = k = 5, k2 = k3 = N), the critical load decreases about 29.43%. For Case 4, comparing Pcr = 17.603 94MN (N = k = 1, k2 = k3 = 1/k) with Pcr = 11.906 23MN (N = k = 5, k2 = k3 = 1/k), the critical load decreases about 32.37%.

|
| Fig. 13 Effects of k on critical pressure qcr (P = 0, N = k, Case 2: k2 = k3 = k, Case 4: k2 = k3 = 1/k) |

|
| Fig. 14 Effects of k on critical load Pcr (q = 0, N = k, Case 2: k2 = k3 = k, Case 4: k2 = k3 = 1/k) |
 |
 |
Tables 10 and 11 and Figs. 15 and 16 illustrate the effects of stiffeners and foundation on the critical compression load Pcr and the critical external pressure load qcr. It can be seen that the buckling increases when the number of stiffeners and the foundation parameters increase. For example, in Table 10, for Case 2, comparing qcr = 1 089.675 38kPa (ns = 10, nr = 20, K1 = 107 N/m3, K2 = 2 × 105 N/m) with qcr = 1 179.774 75kPa (ns = 30, nr = 50, K1 = 107 N/m3, K2 = 2× 105 N/m), we can see that the critical load increases about 7.6%.
 |
 |

|
| Fig. 15 Effects of stiffeners and foundation on critical pressure qcr (P = 0 and k2 = k3 = N = k = 1) |

|
| Fig. 16 Effects of stiffeners and foundation on critical load Pcr (q = 0 and k2 = k3 = N = k = 1) |
An analytical solution is presented to investigate the buckling of ES-FGM-core layer-FGM truncated conical filled inside by an elastic medium and subjected to axial compressive load and uniform pressure. The material properties of stiffeners are graded in the thickness direction according to a volume fraction general sigmoid distribution. The change of spacing between stringers in the meridional direction is taken into account. The couple set of three variable coefficient partial differential equations is investigated by the Galerkin method, and the closedform expression for determining the critical buckling load is obtained. The accuracy of the present study is validated by comparing with the available results in the related literature.
Some remarks are obtained from the present results.
(i) The critical buckling load of ES-FGM coated truncated conical shell increases considerably when the thickness of core-to-FGM coating layer a/hFG ratio increases in Cases 3 and 4, and reversely in Cases 1 and 2.
(ii) The critical loads decrease when the semi-vertex angle α increases.
(iii) The stiffeners, the foundation parameters K1, K2, R/hFG, or L/R ratios, and the volume fraction indices k, N, k2, and k3 strongly affect the critical buckling load.
(iv) The critical pressure qcr decreases with the increase of the pre-loaded axial compression load P, and the critical axial compression load Pcr decreases when the pre-loaded pressure q increases.
Appendix A
in which es and er represent the eccentricities of stiffeners with respect to the middle surface of shell (see Fig. 1).
For the FGM-metal core-FGM conical shell,

Case 2 Inside stiffener

For the FGM-ceramic core-FGM conical shell,

Case 3 Outside stiffener

Case 4 Inside stiffener

In Eq. (21),


| [1] | Timoshenko, S. P. and Gere, J. M. Theory of Elastic Stability, Mc Graw-Hill, New York (1961) |
| [2] | Brush, D. O. and Almroth, B. O. Buckling of Bars, Plates and Shells, Mc Graw-Hill, New York (1975) |
| [3] | Volmir, A. S. Stability of Elastic Systems (in Russian), Science Ed., Moscow (1963) |
| [4] | Reddy, J. N. Mechanics of Laminated Composite Plates and Shells, Theory and Analysis, CRC Press, Boca Raton (2004) |
| [5] | Shen, H. S. Functionally Graded Materials, Nonlinear Analysis of Plates and Shells, CRC Press, Taylor and Francis Group, Boca Raton (2009) |
| [6] | Seide, P. Buckling of circular cones under axial compression. Journal of Applied Mechanics, 28, 315-326(1961) |
| [7] | Singer, J. Buckling of circular conical shells under axisymmetrical external pressure. Journal of Mechanical Engineering Science, 3, 330-339(1961) |
| [8] | Baruch, M., Harari, O., and Singer, J. Low buckling loads of axially compressed conical shells. Journal of Applied Mechanics, 37, 384-392(1970) |
| [9] | Tani, J. and Yamaki, Y. Buckling of truncated conical shell under axial compression. AIAA Journal, 8, 568-570(1970) |
| [10] | Tong, L. and Wang, T. K. Buckling analysis of laminated composite conical shells. Composites Science and Technology, 47, 57-63(1993) |
| [11] | Pariatmono, N. and Chryssanthopoulos, M. K. Asymmetric elastic buckling of axially compressed conical shells with various endconditions. AIAA Journal, 33, 2218-2227(1995) |
| [12] | Spagnoli, A. Koiter circles in the buckling of axially compressed conical shells. International Journal of Solids and Structures, 40, 6095-6109(2003) |
| [13] | Lam, K. Y., Li, H., Ng, T. Y., and Chua, C. F. Generalized differential quadrature method for the free vibration of truncated conical panels. Journal of Sound and Vibration, 251, 329-348(2002) |
| [14] | Liew, K. M., Ng, T. Y., and Zhao, X. Free vibration analysis of conical shells via the element-free kp-Ritz method. Journal of Sound and Vibration, 281, 627-645(2005) |
| [15] | Civalek, O. An efficient method for free vibration analysis of rotating truncated conical shells. International Journal of Pressure Vessels and Piping, 83, 1-12(2006) |
| [16] | Sofiyev, A. H. The buckling of FGM truncated conical shells subjected to combined axial tension and hydrostatic pressure. Composite Structures, 92, 488-498(2010) |
| [17] | Sofiyev, A. H. The vibration and stability behavior of freely supported FGM conical shells subjected to external pressure. Composite Structures, 89, 356-366(2009) |
| [18] | Sofiyev, A. H. Non-linear buckling behavior of FGM truncated conical shells subjected to axial load. International Journal of Non-Linear Mechanics, 46, 711-719(2011) |
| [19] | Sofiyev, A. H. The non-linear vibration of FGM truncated conical shells. Composite Structures, 94, 2237-2245(2012) |
| [20] | Sofiyev, A. H. The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler-Pasternak foundations. International Journal of Pressure Vessels and Piping, 87, 753-761(2010) |
| [21] | Naj, R., Boroujerdy, M. S., and Eslami, M. R. Thermal and mechanical instability of functionally graded truncated conical shells. Thin-Walled Structures, 46, 65-78(2008) |
| [22] | Bich, D. H., Phuong, N. T., and Tung, H. V. Buckling of functionally graded conical panels under mechanical loads. Composite Structures, 94, 1379-1384(2012) |
| [23] | Malekzadeh, P. and Heydarpour, Y. Free vibration analysis of rotating functionally graded truncated conical shells. Composite Structures, 97, 176-188(2013) |
| [24] | Liew, K. M., Yang, J., and Wu, Y. F. Nonlinear vibration of a coating-FGM-substrate cylindrical panel subjected to a temperature gradient. Computer Methods in Applied Mechanics and Engineering, 195, 1007-1026(2006) |
| [25] | Alibeigloo, A. and Liew, K. M. Free vibration analysis of sandwich cylindrical panel with functionally grade core using three-dimensional theory of elasticity. Composite Structures, 113, 23-30(2014) |
| [26] | Li, S. R. and Batra, R. C. Buckling of axially compressed thin cylindrical shells with functionally graded middle layer. Thin-Walled Structures, 44, 1039-1047(2006) |
| [27] | Sofiyev, A. H. and Kuruoglu, N. Torsional vibration and buckling of the cylindrical shell with functionally graded coatings surrounded by an elastic medium. Composites:Part B, 45, 1133-1142(2013) |
| [28] | Sofiyev, A. H. The vibration and buckling of sandwich cylindrical shells covered by different coatings subjected to the hydrostatic pressure. Composite Structures, 117, 124-134(2014) |
| [29] | Najafov, A. M., Sofiyev, A. H., and Kuruoglu, N. On the solution of nonlinear vibration of truncated conical shells covered by functionally graded coatings. Acta Mechanica, 225, 563-580(2014) |
| [30] | Sofiyev, A. H., Zerin, Z., and Korkmaz, A. The stability of a thin three-layered composite truncated conical shell containing an FGM layer subjected to non-uniform lateral pressure. Composite Structures, 85, 105-115(2008) |
| [31] | Deniz, A. Nonlinear stability analysis of truncated conical shell with functionally graded composite coatings in the finite deflection. Composites:Part B, 51, 318-326(2013) |
| [32] | Sofiyev, A. H. On the dynamic buckling of truncated conical shells with functionally graded coatings subjected to a time dependent axial load in the large deformation. Composites:Part B, 58, 524-533(2014) |
| [33] | Weingarten, V. I. Free vibration of ring stiffened conical shells. AIAA Journal, 3, 1475-1481(1965) |
| [34] | Crenwelge, O. E. and Muster, D. Free vibration of ring and stringer stiffened conical shells. The Journal of Acoustical Society of America, 46, 176-185(1969) |
| [35] | Mustaffa, B. A. J. and Ali, R. Free vibration analysis of multi-symmetric stiffened shells. Computers and Structures, 27, 803-810(1987) |
| [36] | Srinivasan, R. S. and Krishnan, P. A. Dynamic analysis of stiffened conical shell panels. Computers and Structures, 33, 831-837(1989) |
| [37] | Mecitoglu, Z. Vibration characteristics of a stiffened conical shell. Journal of Sound and Vibration, 197, 191-206(1996) |
| [38] | Rao, S. S. and Reddy, E. S. Optimum design of stiffened conical shells with natural frequency constraints. Computers and Structures, 14, 103-110(1981) |
| [39] | Najafizadeh, M. M., Hasani, A., and Khazaeinejad, P. Mechanical stability of functionally graded stiffened cylindrical shells. Applied Mathematical Modelling, 33, 1151-1157(2009) |
| [40] | Dung, D. V. and Hoa, L. K. Nonlinear buckling and post-buckling analysis of eccentrically stiffened functionally graded circular cylindrical shells under external pressure. Thin-Walled Structures, 63, 117-124(2013) |
| [41] | Dung, D. V. and Hoa, L. K. Research on nonlinear torsional buckling and post-buckling of eccentrically stiffened functionally graded thin circular cylindrical shells. Composite:Part B, 51, 300-309(2013) |
| [42] | Bich, D. H., Dung, D. V., and Nam, V. H. Nonlinear dynamical analysis of eccentrically stiffened functionally graded cylindrical panels. Composite Structures, 94, 2465-2473(2012) |
| [43] | Bich, D. H., Dung, D. V., and Nam, V. H. Nonlinear dynamic analysis of eccentrically stiffened imperfect functionally graded doubly curved thin shallow shells. Composite Structures, 96, 384-395(2013) |
| [44] | Dung, D. V. and Nam, V. H. Nonlinear dynamic analysis of eccentrically stiffened functionally graded circular cylindrical thin shells under external pressure and surrounded by an elastic medium. European Journal of Mechanics A/Solids, 46, 42-53(2014) |
| [45] | Dung, D. V., Hoa, L. K., Nga, N. T., and Anh, L. T. N. Instability of eccentrically stiffened functionally graded truncated conical shells under mechanical loads. Composite Structures, 106, 104-113(2013) |
 2016, Vol. 37
2016, Vol. 37




