Shanghai University
Article Information
- R. ANSARI, T. POURASHRAF, R. GHOLAMI, H. ROUHI. 2016.
- Analytical solution approach for nonlinear buckling and postbuckling analysis of cylindrical nanoshells based on surface elasticity theory
- Appl. Math. Mech. -Engl. Ed., 37(7): 903-918
- http://dx.doi.org/10.1007/s10483-016-2100-9
Article History
- Received 2016-01-27;
- in final form 2016-03-28
2. Department of Mechanical Engineering, Lahijan Branch, Islamic Azad University, Lahijan 1616, Iran;
3. Department of Engineering Science, Faculty of Technology and Engineering, East of Guilan, University of Guilan, Rudsar-Vajargah 44891-63157, Iran
Theoretical investigations on the behavior of nanostructures are generally performed via atomistic simulations and continuum models. Although the accuracy of atomistic simulation is very high, their computational cost is noticeably higher than that of continuum approaches especially for nanostructures with a large number of atoms. As a result, continuum models as computationally efficient tools are extensively used for modeling nanostructures with a large number of atoms. Classical continuum models are size-independent, making their applicability to nanostructures questionable. As the size of nanostructures is scaled down to very small scales, size effects play an important role in their mechanical behavior. Thus, classical continuum models need to be extended in order to take the size effects into account. Up to now, several nonclassical continuum theories have been developed for considering the small scale effects in the analysis of micro- and nanostructures. The nonlocal[1, 2], couple stress[3, 4, 5], strain gradient[6, 7, 8], micropolar, and micromorphic[9, 10] theories can be mentioned for example.
The nonlocal effect is one of the size effects which cannot be taken into account by the classical continuum mechanics. Such an effect is due to the discrete nature of matter and can be captured based on the Eringen nonlocal elasticity theory[1, 2]. There are several research works in the literature on the mechanical problems of nanostructures in which nonlocal beam, plate, and shell models have been used[11, 12, 13, 14, 15, 16, 17, 18, 19, 20].
The surface stress is another important small scale influence that can significantly affect the mechanical behavior of ultra-thin nanostructures. The concept of surface stress in solids was first proposed by Gibbs[21]. It can be briefly explained as follows. Atoms at or near a free surface of a solid body have different equilibrium requirements in comparison with those within the bulk of material as a consequence of different environmental conditions. Because the energies of atoms located on the surface or near to it are different from those of atoms in the bulk phase, creation of a surface leads to an excess free energy in the solid which is called the surface free energy, and the surface stress is defined based on the variation of surface free energy with the surface strain. In nanostructures for which the surface-to-volume ratio is very high, the surface stress effect plays an important role in their mechanical behavior. In this regard, Cammarata[22] commented that for a solid phase with one or more of its dimensions smaller than about 10 nm, the surface and interface stresses can be principal factors in determining the equilibrium structure and behavior of the solid.
So as to incorporate the surface stress effect into the continuum mechanics, Gurtin and Murdoch[23, 24] developed a non-classical continuum theory. In the Gurtin-Murdoch model, the surface stress was formulated as a function of the deformation gradient, and the surface was treated as a mathematical layer with zero thickness perfectly bonded to the bulk of material. Several research papers on the mechanics of nanorods[25], nanobeams[26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39], nanoplates[40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53], nanowires[54, 55, 56, 57], and nanoshells[58, 59] can be found, in which the surface stress has been taken into consideration using such a continuum model. Eltaher et al.[27] studied the coupling effects of surface energy and nonlocal elasticity on the vibration behavior of nanobeams based on a finite element approach. In order to capture the surface effects, they developed a sizedependent Euler-Bernoulli beam model based on the Gurtin-Murdoch theory. Amirian et al.[31] investigated the free vibration characteristics of Timoshenko nanobeams made of alumina in the presence of surface and thermal effects resting on a Pasternak foundation. Their results indicated that the surface effects result in an increase in the natural frequency of nanobeams. The asymmetric bifurcation of initially curved Euler-Bernoulli nanobeams with considering surface effects was analyzed by Chen and Meguid[34]. Wang and Wang[36] presented a continuum model for nano-cantilever switches including surface effects and nonlinear curvature. Radebe and Adali[51] studied the influence of surface stress on the buckling response of nonlocal nanoplates subjected to material uncertainty. The surface stress effect on the stiffness of micro- and nano-cantilevers was also probed by Qiao and Zheng[57].
Nanoshells have recently attracted attention of researchers for several applications[60]. In some of these applications, accurate identification of buckling and postbuckling behaviors of the nanoshell can be very significant from the designing point of view. At the macroscale, the postbuckling characteristics of shells have been widely studied[61, 62, 63, 64, 65]. However, research works on the postbuckling behavior of nanoshells with considering the size effects are very limited. Also, a literature survey shows that the surface effects have been extensively investigated on the mechanical behavior of nanobeams, nanoplates, and nanowires. However, the mechanical responses of nanoshells with the consideration of such important effects have been rarely investigated up to now. The limited number of research works on the size-dependent shell models might be because of the difficulty of derivation and solution of non-classical shell equations including small scale effects that are obviously more complex than their beam and plate counterparts.
In the present paper, an analytical size-dependent shell model including the surface effects is proposed to address nonlinear buckling and postbuckling problems of cylindrical nanoshells subjected to the axial compressive load. To this end, within the framework of Gurtin-Murdoch surface elasticity theory, a Donnell-type shell model is developed first. The geometric nonlinearity is taken into account using the von K´arm´an assumption. Then, in the context of variational formulation, an efficient analytical approach is used for the solution procedure. The selected numerical results are presented for investigating the effects of the surface stress, the surface residual tension, and the radius-to-thickness ratio on prebuckling and postbuckling characteristics of nanoshells.
2 Formulation of problemConsider a circular cylindrical nanoshell with the length L, the thickness h, and the midsurface radius R as indicated in Fig. 1. A bulk part and two thin surface layers (inner and outer layers) are considered for the nanoshell. For the bulk part, one has Young’s modulus E and Poisson’s ratio ν. Also, the two surface layers are considered to have the surface Lam´e constants of λs and μs and the surface residual tension τs.

|
| Fig. 1 Schematic of circular cylindrical nanoshell: kinematic parameters, coordinate system, and geometry |
With reference to a coordinate system (x, y, z) with its origin located on the middle surface of nanoshell, the coordinates of a typical point in the axial, circumferential, and radial directions are denoted by x, y, and z, respectively. On the basis of the classical deformation shell theory and Love’s hypotheses, because of assuming zero transverse shear deformation, the rotation of the normal is related to the slope of the mid-surface after deformation. Therefore, the displacement field can be written as follows[66]:
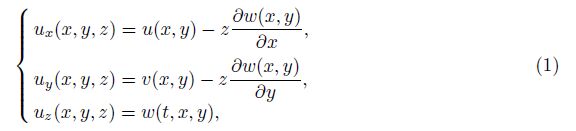
in which u, v, and w denote the middle surface displacements.
Following the classical Donnell shell theory[67] which assumes that the thickness of the shell h is remarkably small as compared with its radius of curvature R, and based on the von K´arm´an hypothesis, the relations between the strain and displacement components are given by
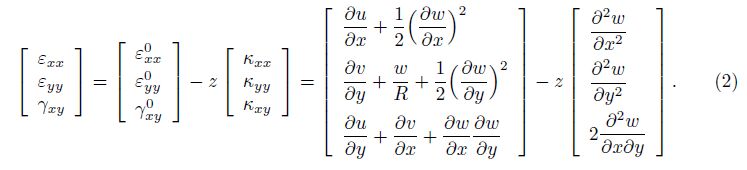
Then, the constitutive relations are expressed as
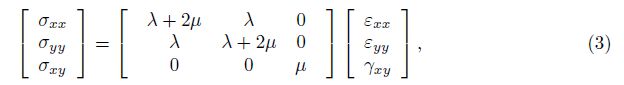
in which λ = Eν/(1 - ν2) and μ = E/(2(1 + ν)) stand for the classical Lam´e constants.
In nanostructures, there are always interactions between the elastic surface and the bulk of material. Therefore, they mostly undergo in-plane loads in different directions. These inplane loads applied on the surfaces of the bulk part result in surface stresses. According to the Gurtin-Murdoch theory, the surface constitutive equations are given by[23]
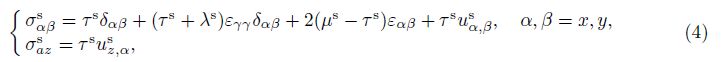
where λs and μs are the surface Lam´e constants. Using Eq. (4), the surface stress components
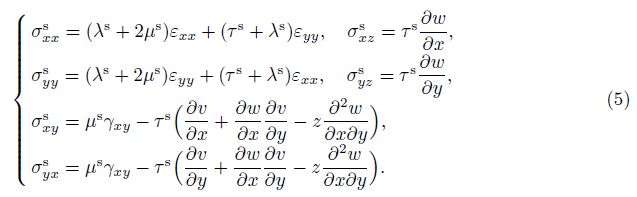
In the classical continuum theories, it is assumed that σzz is equal to zero, because it is small in comparison with the other normal stresses. However, this assumption does not satisfy the surface conditions of the Gurtin-Murdoch theory. In order to solve this problem, it is assumed that σzz varies linearly through the thickness of nanoshell and satisfies the balance conditions on the surfaces. Hence, σzz is obtained as
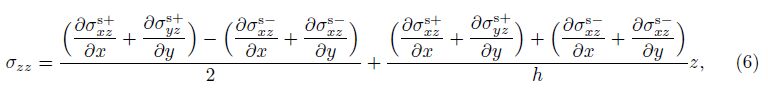
where the superscripts s+ and s- show the outer and inner layers, respectively.
Using Eq. (5) leads to
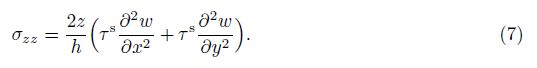
In addition, the normal stresses (σxx, σyy) for the bulk of the nanoshell are written as
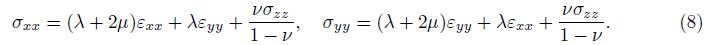
The total strain energy of the nanoshell including the surface stress effect can be formulated as
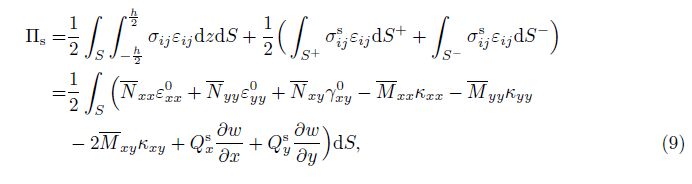
where S is the area occupied by the middle plane of the nanoshell. In Eq. (9), the in-plane force resultants, the bending moments, and the shear forces are expressed as
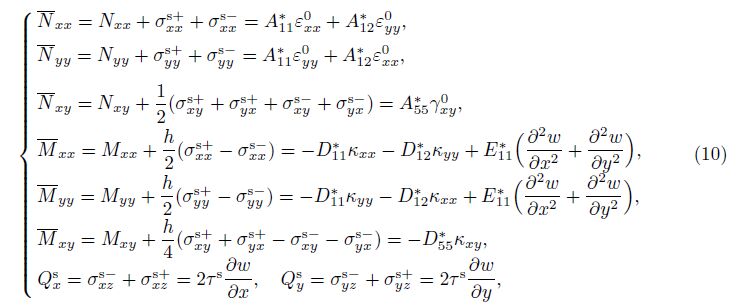
in which
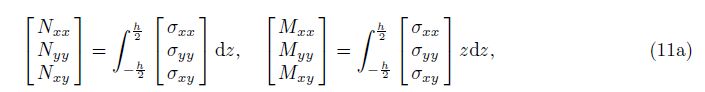
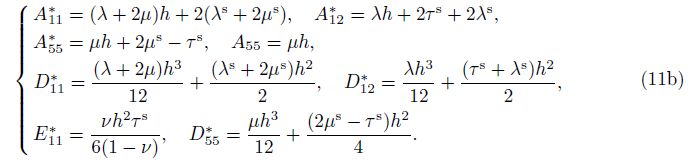
Now from Eq. (2), the compatibility equation is obtained as
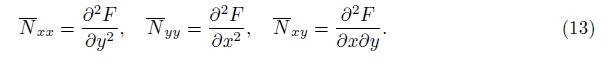
Substituting Eq. (13) into Eq. (10) yields
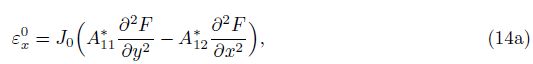
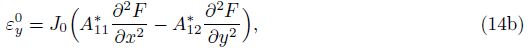

where
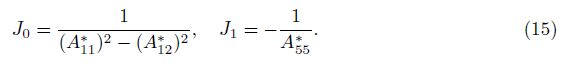
By inserting Eq. (14) into Eq. (12), one can obtain
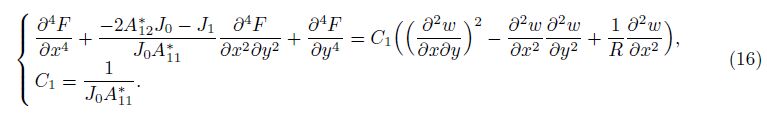
Substituting Eqs. (13) and (14) into Eq. (9) yields
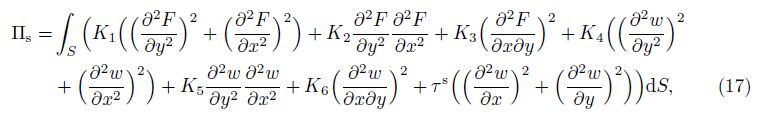
where
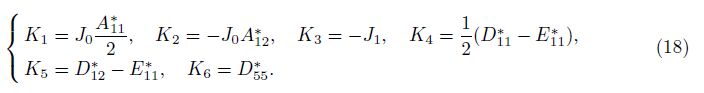
It is assumed that the nanoshell is subjected to an axial load. By means of Eqs. (2) and (14), the work done by the external forces is
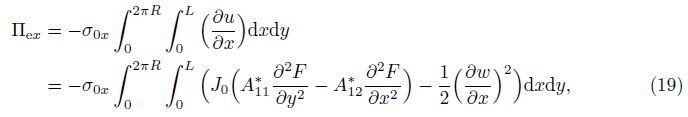
where σ0x is the average axial stress on the end sections of nanoshell and is positive for the compression.
The total potential energy of the system is

Based on Eqs. (2) and (14),
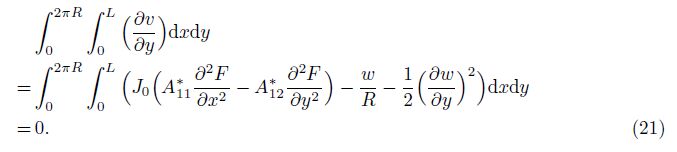
Similarly, the average end-shortening ratio of the nanoshell can be given as
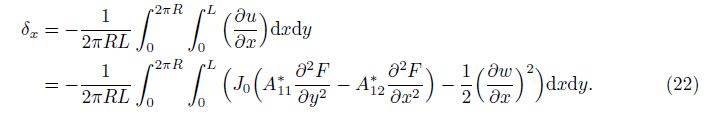
The deflection of combined axially and laterally loaded shells under simply-supported boundary conditions can be expressed as follows[68]:
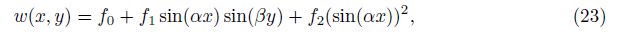
in which α = mπ/L, β = n/R, and m and n are the axial half-wave number along the x-axis and the wave number along the y-axis, respectively. Also, f0, f1, and f2 are unknown amplitudes. f0 denotes the uniform deflection in the prebuckling state. f1 sin(αx) sin(βy) expresses the linear buckling shape, and f2(sin(αx))2 represents the nonlinear diamond buckling shape of large deflection.
Substitution of Eq. (23) into Eq. (16) yields
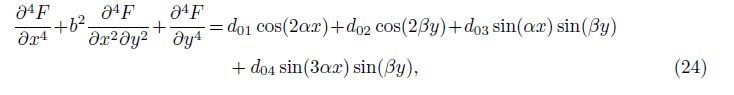
where
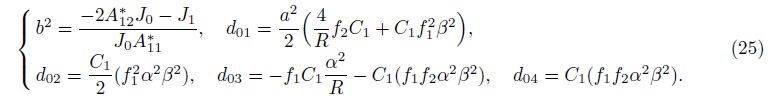
Then, the general solution of F is given by
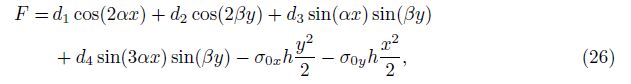
in which σ0y signifies the average circumferential stress and is positive when the nanoshell is circumferentially compressed. The other parameters are introduced as
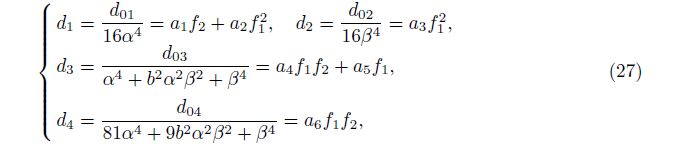
where
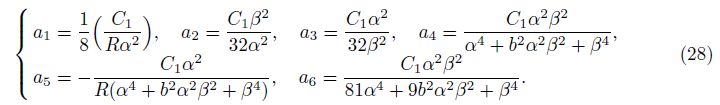
By Eqs. (23) and (26), Eqs. (17) and (19) are rewritten as
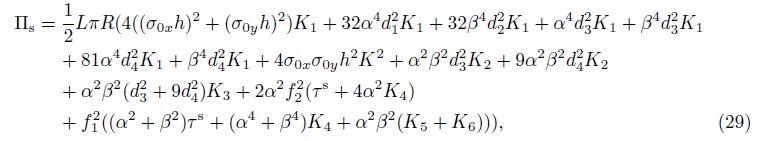
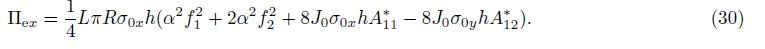
By substituting Eqs. (29) and (30) into Eq. (20), the total potential energy is obtained, and the Ritz energy method is then applied as
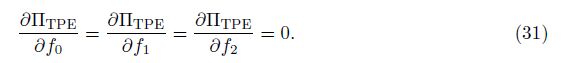
By Eqs. (23) and (26), Eq. (21) becomes
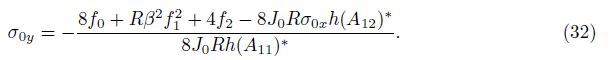
Through inserting Eq. (32) into Eq. (20), and then from Eq. (31), one has
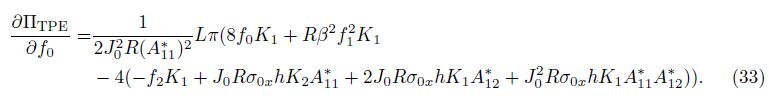
Considering Eqs. (32) and (33) leads to

As this equation is satisfied, the close condition and  hold simultaneously. This
indicates that the prebuckling circumferential stress should be related only to the radial pressure
when the shell can freely move in the radial direction. By considering Eq. (34) in the last two
partial derivatives of Eq. (31) and noting that f1 ≠ 0, one has
hold simultaneously. This
indicates that the prebuckling circumferential stress should be related only to the radial pressure
when the shell can freely move in the radial direction. By considering Eq. (34) in the last two
partial derivatives of Eq. (31) and noting that f1 ≠ 0, one has
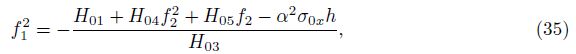
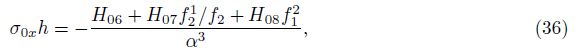
where
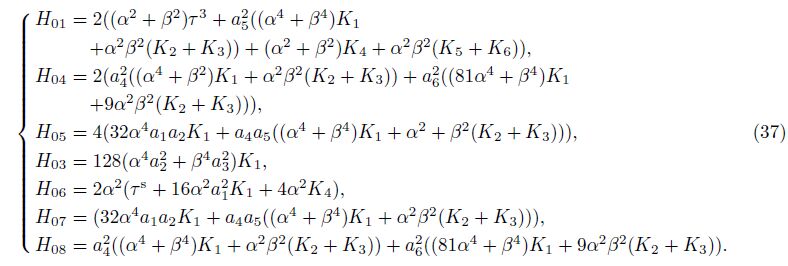
According to Eqs. (36) and (37), one achieves the following relation:
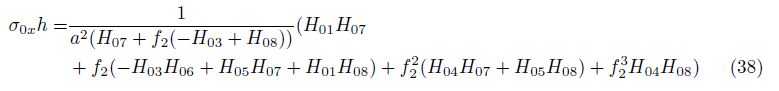
that can be used to obtain the nonlinear critical condition for the axially loaded circular cylindrical nanoshell. By dropping the nonlinear buckling shape (f2 = 0), the linear critical axial load is calculated.
With the use of Eq. (34), substituting Eqs. (23) and (26) into Eq. (22) yields the expression of the end shortening ratio of the nanoshell as
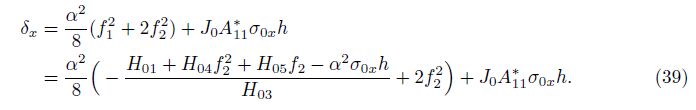
In this section, selected numerical results are presented for nonlinear buckling and postbuckling characteristics of nanoshells under the axial compressive load with and without considering the surface stress effect. The nanoshells are assumed to be made of two materials including Si (100) and Al (111). The material properties of bulk and surface layers of nanoshell used to generate the numerical results are given in Table 1[54, 69, 70]. Also, the dimensions of the nanoshells considered here are selected in accordance with the experimental evidences[60, 71].
As it was mentioned earlier, the nonlinear critical condition for the axially loaded nanoshell can be obtained through Eq. (38). The nonlinear critical condition is defined here as the possible lowest point of external axial load[72]. Figures 2 and 3 show the diagrammatic sketch of solving the nonlinear critical axial stress and the buckling mode of nanoshells made of Si and Al based on the classical and surface elasticity theories. In these figures, for different combinations of mode numbers (m, n), σx0 is plotted against f2/h using Eq. (38). From the lowest point of the envelope curve (indicated by solid lines), the nonlinear critical condition with the nonlinear critical axial stress and the associated nonlinear buckling mode can be extracted.

|
| Fig. 2 Diagrammatic sketch of solving nonlinear critical axial stress and buckling mode of nanoshells made of Si and Al based on classical elasticity theory (h = 10 nm, L = R, R = 200h, and n = 4, 5, …, 9) |

|
| Fig. 3 Diagrammatic sketch of solving nonlinear critical axial stress and buckling mode of nanoshells made of Si and Al based on surface elasticity theory (h = 50 nm, L = R, and R = 200h) |
In Fig. 4, the postbuckling paths of nanoshells made of Si and Al are shown, in which the solid lines specify the postbuckling equilibrium path. It is seen that the structure follows a prebuckling path before reaching the linear bifurcation point. At this point, the axial stress has its maximum value (the linear critical load or the upper critical load). It is then observed that the structure follows the postbuckling path and the axial stress noticeably decreases up to the minimum value which corresponds to the lower critical load. After that, the stress slightly increases. According to the figure, continuous mode jumps are also observed in the postbuckling regions (m = 1, n = 8, 7, …, 4 in the case of Si, and m = 1, n = 6, 5, …, 3 in the case of Al).

|
| Fig. 4 Diagrammatic sketch of load-shortening ratio response curve of nanoshells made of Si and Al based on surface elasticity theory (h = 10 nm, L = R, and R = 200h) |
Figure presents the postbuckling paths of the nanoshells made of Si and Al based on both classical and surface elasticity theories. In this figure, the influence of material type is highlighted. As it can be seen that there is a considerable difference between the prebuckling and postbuckling paths of the nanoshells made of Si and Al when the surface effects are taken into account. It is observed that the curve corresponding to Al is higher than that for Si.
Figure 5 shows the postbuckling paths of nanoshells made of Si with different thicknesses including the surface effects. The results from the classical elasticity theory are also provided in this figure for comparison purpose. It is seen that as the thickness of nanoshell decreases, the surface stress effect becomes more prominent leading to the increase of carrying capacity of nanoshell. Figure 6 indicates that the upper and lower critical loads get larger and the postbuckling equilibrium path moves upward with decreasing the thickness of nanoshell. Moreover, one can find that the difference between the results of two theories is considerable at small values of thickness, but it becomes insignificant by increasing the thickness. It can be explained by the fact that with decreasing the thickness of nanoshell, the energies of surface layers become considerable as compared with those of bulk of material. However, with increasing the thickness of nanoshell, the energies of the bulk phase increase, and thus the surface energies become negligible.

|
| Fig. 5 Effect of material type on load-shortening ratio response curve of nanoshells based on classical elasticity theory and surface elasticity theory (L = R, R = 200h, and h = 50 nm) |

|
| Fig. 6 Effect of surface stress on load-shortening ratio response curve of nanoshell made of Si (L = R, R = 200h, and n = 4, 5, …, 9) |
Figure 7 highlights the influence of the surface residual tension on the postbuckling paths of nanoshell made of Si. It is observed that the buckling behavior of nanoshell is dependent on the selected value for τs. It is seen that by selecting a positive value for the surface residual tension, the upper and lower critical axial loads increase, and the postbuckling equilibrium path moves upward, whereas the negative value has a reverse effect. The reason for such behaviors is that the tensile and compressive in-plane forces are generated in the nanoshell due to the positive and negative surface residual tensions, respectively.

|
| Fig. 7 Effect of surface residual tension on load-shortening ratio response curve of nanoshell made of Si (h = 60 nm, L = R, R = 200h, and n = 4, 5, …, 9) |
Figure 8 represents the effect of the radius-to-thickness ratio on prebuckling and postbuckling characteristics of the nanoshell. It is observed that by increasing this ratio, the lower critical load decreases, and the postbuckling equilibrium path moves downward.

|
| Fig. 8 Effect of radius-to-thickness ratio on load-shortening ratio response curve of nanoshell made of Si based on surface elasticity theory (h = 50 nm and L = R) |
The geometrically nonlinear buckling and postbuckling characteristics of circular cylindrical nanoshells subjected to the axial compressive load including the surface effects are investigated based on an analytical approach. To accomplish this aim, a Donnell-type shell model is first developed, whose geometric nonlinearity is captured based on the von K´arm´an hypothesis. The surface effects are also incorporated into the model according to the Gurtin-Murdoch theory. The selected numerical results are provided on prebuckling and postbuckling characteristics of nanoshells made of Si and Al based on both classical and Gurtin-Murdoch theories. It is shown that there is a considerable difference between the prebuckling and postbuckling paths of the nanoshells made of Si and Al as the surface stress effect is considered. It is also concluded that due to the surface stress effect, the upper and lower critical loads increase, and the postbuckling equilibrium path moves upward when the thickness of nanoshell decreases. The results reveal that the surface energies have significant influence on the postbuckling behavior of very thin nanoshells, but their effect becomes negligible when the thickness is sufficiently large. Another finding is that the surface stress effect is dependent on the value of surface residual tension.
| [1] | Eringen, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54(9), 4703-4710(1983) |
| [2] | Eringen, A. C. Nonlocal Continuum Field Theories, Springer, New York (2002) |
| [3] | Mindlin, R. D. and Tiersten, H. F. Effects of couple-stresses in linear elasticity. Archive for Rational Mechanics and Analysis, 11(1), 415-448(1962) |
| [4] | Koiter, W. T. Couple stresses in the theory of elasticity. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen (B), 67(1), 17-44(1964) |
| [5] | Yang, F., Chong, A. C. M., Lam, D. C. C., and Tong, P. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 39(10), 2731-2743(2002) |
| [6] | Mindlin, R. D. Micro-structure in linear elasticity. Archive for Rational Mechanics and Analysis, 6(1), 51-78(1964) |
| [7] | Mindlin, R. D. Second gradient of strain and surface tension in linear elasticity. International Journal of Solids and Structures, 1(4), 417-438(1965) |
| [8] | Lam, D. C. C., Yang, F., Chong, A. C. M., Wang, J., and Tong, P. Experiments and theory in strain gradient elasticity. Journal of the Mechanics and Physics of Solids, 51(8), 1477-1508(2003) |
| [9] | Eringen, A. C. and Suhubi, E. Nonlinear theory of simple micro-elastic solids-I. International Journal of Engineering Science, 2(2), 189-203(1964) |
| [10] | Suhubi, E. and Eringen, A. C. Nonlinear theory of micro-elastic solids-Ⅱ. International Journal of Engineering Science, 2(4), 389-404(1964) |
| [11] | Ansari, R., Arash, B., and Rouhi, H. Vibration characteristics of embedded multi-layered graphene sheets with different boundary conditions via nonlocal elasticity. Composite Structures, 93(9), 2419-2429(2011) |
| [12] | Peddieson, J., Buchanan, G. R., and McNitt, R. P. Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science, 41(3-5), 305-312(2003) |
| [13] | Sudak, L. J. Column buckling of multiwalled carbon nanotubes using nonlocal continuum mechanics. Journal of Applied Physics, 94(11), 7281-7287(2003) |
| [14] | Rouhi, H. and Ansari, R. Nonlocal analytical flugge shell model for axial buckling of double-walled carbon nanotubes with different end conditions. Nano, 7, 1250018(2012) |
| [15] | Ansari, R. and Rouhi, H. Analytical treatment of the free vibration of single-walled carbon nanotubes based on the nonlocal flugge shell theory. Journal of Engineering Materials and Technology, 134(1), 011008(2012) |
| [16] | Chang, T. P. Thermal-mechanical vibration and instability of a fluid-conveying single-walled carbon nanotube embedded in an elastic medium based on nonlocal elasticity theory. Applied Mathematical Modelling, 36(5), 1964-1973(2012) |
| [17] | Wang, K. F., Wang, B. L., and Kitamura, T. A review on the application of modified continuum models in modeling and simulation of nanostructures. Acta Mechanica Sinica, 32(1), 83-100(2016) |
| [18] | Ansari, R., Gholami, R., and Rouhi, H. Size-dependent nonlinear forced vibration analysis of magneto-electro-thermo-elastic Timoshenko nanobeams based upon the nonlocal elasticity theory. Composite Structures, 126, 216-226(2015) |
| [19] | Ansari, R., Rouhi, H., and Sahmani, S. Calibration of the analytical nonlocal shell model for vibrations of double-walled carbon nanotubes with arbitrary boundary conditions using molecular dynamics. International Journal of Mechanical Sciences, 53(9), 786-792(2011) |
| [20] | Ansari, R. and Rouhi, H. Explicit analytical expressions for the critical buckling stresses in a monolayer graphene sheet based on nonlocal elasticity. Solid State Communications, 152(2), 56-59(2012) |
| [21] | Gibbs, J. W. The Scientific Papers of J. Willard Gibbs, Vol. 1, Longmans-Green, London (1906) |
| [22] | Cammarata, R. C. Surface and interface stress effects on interfacial and nanostructured materials. Materials Science and Engineering, A237(2), 180-184(1997) |
| [23] | Gurtin, M. E. and Murdoch, A. I. A continuum theory of elastic material surfaces. Archive for Rational Mechanics and Analysis, 57(4), 291-323(1975) |
| [24] | Gurtin, M. E. and Murdoch, A. I. Surface stress in solids. International Journal of Solids and Structures, 14(6), 431-440(1978) |
| [25] | Arefi, M. Surface effect and non-local elasticity in wave propagation of functionally graded piezoelectric nano-rod excited to applied voltage. Applied Mathematicsand Mechanics (English Edition), 37(3), 289-302(2016) DOI 10.1007/s10483-016-2039-6 |
| [26] | Ansari, R. and Sahmani, S. Bending behavior and buckling of nanobeams including surface stress effects corresponding to different beam theories. International Journal of Engineering Science, 49(11), 1244-1255(2011) |
| [27] | Eltaher, M. A., Mahmoud, F. F., Assie, A. E., and Meletis, E. I. Coupling effects of nonlocal and surface energy on vibration analysis of nanobeams. Applied Mathematics and Computation, 224, 760-774(2013) |
| [28] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Sahmani, S. Postbuckling characteristics of nanobeams based on the surface elasticity theory. Composites Part B:Engineering, 55, 240-246(2013) |
| [29] | Hossieni-Hashemi, S. and Nazemnezhad, R. An analytical study on the nonlinear free vibration of functionally graded nanobeams incorporating surface effects. Composites Part B:Engineering, 52, 199-206(2013) |
| [30] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Rouhi, H. Nonlinear vibration analysis of Timoshenko nanobeams based on surface stress elasticity theory. European Journal of Mechanics-A/Solids, 45, 143-152(2014) |
| [31] | Amirian, B., Hosseini-Ara, R., and Moosavi, H. Surface and thermal effects on vibration of embedded alumina nanobeams based on novel Timoshenko beam model. Applied Mathematics and Mechanics (English Edition), 35(7), 875-886(2014) DOI 10.1007/s10483-014-1835-9 |
| [32] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Sahmani, S. Postbuckling analysis of Timoshenko nanobeams including surface stress effect. International Journal of Engineering Science, 75, 1-10(2014) |
| [33] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Sahmani, S. On the forced vibration analysis of Timoshenko nanobeams based on the surface stress elasticity theory. Composites Part B:Engineering, 60, 158-166(2014) |
| [34] | Chen, X. and Meguid, S. A. Asymmetric bifurcation of initially curved nanobeam. Journal of Applied Mechanics, 82, 091003(2015) |
| [35] | Ansari, R., Gholami, R., Norouzzadeh, A., and Darabi, M. A. Surface stress effect on the vibration and instability of nanoscale pipes conveying fluid based on a size-dependent Timoshenko beam model. Acta Mechanica Sinica, 31(5), 708-719(2015) |
| [36] | Wang, K. F. and Wang, B. L. A general model for nano-cantilever switches with consideration of surface effects and nonlinear curvature. Physica E, 66, 197-208(2015) |
| [37] | Ansari, R., Pourashraf, T., and Gholami, R. An exact solution for the nonlinear forced vibration of functionally graded nanobeams in thermal environment based on surface elasticity theory. Thin-Walled Structures, 93, 169-176(2015) |
| [38] | Lu, Z., Xie, F., Liu, Q., and Yang, Z. Surface effects on mechanical behavior of elastic nanoporous materials under high strain. Applied Mathematics and Mechanics (English Edition), 36(7), 927-938(2015) DOI 10.1007/s10483-015-1958-9 |
| [39] | Duan, J., Li, Z., and Liu, J. Pull-in instability analyses for NEMS actuators with quartic shape approximation. Applied Mathematics and Mechanics (English Edition), 37(3), 303-314(2016) DOI 10.1007/s10483-015-2007-6 |
| [40] | He, L. H., Lim, C. W., and Wu, B. S. A continuum model for size-dependent deformation of elastic film of nano-scale thickness. International Journal of Solids and Structures, 41(3), 847-857(2004) |
| [41] | Ansari, R. and Sahmani, S. Surface stress effects on the free vibration behavior of nanoplates. International Journal of Engineering Science, 49(11), 1204-1215(2011) |
| [42] | Lu, P., He, L. H., Lee, H. P., and Lu, C. Thin plate theory including surface effects. International Journal of Solids and Structure, 43(16), 4631-4647(2006) |
| [43] | Ansari, R., Gholami, R., Faghih-Shojaei, M., Mohammadi, V., and Darabi, M. A. Surface stress effect on the pull-in instability of hydrostatically and electrostatically actuated rectangular nanoplates with various edge supports. Journal of Engineering Materials and Technology, 134(4), 041013(2012) |
| [44] | Huang, D. W. Size-dependent response of ultra-thin films with surface effects. International Journal of Solids and Structures, 45(2), 568-579(2008) |
| [45] | Ansari, R., Gholami, R., Faghih-Shojaei, M., Mohammadi, V., and Sahmani, S. Surface stress effect on the vibrational response of circular nanoplates with various edge supports. Journal of Applied Mechanics, 80(2), 021021(2013) |
| [46] | Narendar, S. and Gopalakrishnan, S. Study of Terahertz wave propagation properties in nanoplates with surface and small-scale effects. International Journal of Mechanical Sciences, 64(1), 221-231(2012) |
| [47] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Sahmani, S. Surface stress effect on the postbuckling and free vibrations of axisymmetric circular Mindlin nanoplates subject to various edge supports. Composite Structures, 112, 358-367(2014) |
| [48] | Shaat, M., Mahmoud, F. F., Gao, X. L., and Faheem, A. F. Size-dependent bending analysis of Kirchhoff nano-plates based on a modified couple-stress theory including surface effects. International Journal of Mechanical Sciences, 79, 31-37(2014) |
| [49] | Ansari, R., Mohammadi, V., Faghih-Shojaei, M., Gholami, R., and Darabi, M. A. A geometrically non-linear plate model including surface stress effect for the pull-in instability analysis of rectangular nanoplates under hydrostatic and electrostatic actuations. International Journal of Non-Linear Mechanics, 67, 16-26(2014) |
| [50] | Ansari, R., Gholami, R., Faghih-Shojaei, M., Mohammadi, V., and Sahmani, S. Surface stress effect on the pull-in instability of circular nanoplates. Acta Astronautica, 102, 140-150(2014) |
| [51] | Radebe, I. S. and Adali, S. Effect of surface stress on the buckling of nonlocal nanoplates subject to material uncertainty. Latin American Journal of Solids and Structures, 56, 840-846(2015) |
| [52] | Ansari, R., Ashrafi, M. A., Pourashraf, T., and Sahmani, S. Vibration and buckling characteristics of functionally graded nanoplates subjected to thermal loading based on surface elasticity theory. Acta Astronautica, 109, 42-51(2015) |
| [53] | Ansari, R., Shahabodini, A., Faghih-Shojaei, M., Mohammadi, V., and Gholami, R. On the bending and buckling behaviors of Mindlin nanoplates considering surface energies. Physica E, 57, 126-137(2014) |
| [54] | Miller, R. E. and Shenoy, V. B. Size-dependent elastic properties of nanosized structural elements. Nanotechnology, 11, 139-147(2000) |
| [55] | Park, H. S. Surface stress effects on the critical buckling strains of silicon nanowires. Computational Materials Science, 51(1), 396-401(2012) |
| [56] | Chiu, M. S. and Chen, T. Bending and resonance behavior of nanowires based on Timoshenko beam theory with high-order surface stress effects. Physica E, 54, 149-156(2013) |
| [57] | Qiao, L. and Zheng, X. Effect of surface stress on the stiffness of micro/nanocantilevers:nanowire elastic modulus measured by nano-scale tensile and vibrational techniques. Journal of Applied Physics, 113(1), 013508(2013) |
| [58] | Rouhi, H., Ansari, R., and Darvizeh, M. Size-dependent free vibration analysis of nanoshells based on the surface stress elasticity. Applied Mathematical Modelling, 40(4), 3128-3140(2016) |
| [59] | Rouhi, H., Ansari, R., and Darvizeh, M. Analytical treatment of the nonlinear free vibration of cylindrical nanoshells based on a first-order shear deformable continuum model including surface influences. Acta Mechanica, 227(2016) DOI 10.1007/s00707-016-1595-4 |
| [60] | Zabow, G., Dodd, S. J., Moreland, J., and Koretsky, A. P. Fabrication of uniform cylindrical nanoshells and their use as spectrally tunable MRI contrast agents. Nanotechnology, 20, 385301(2009) |
| [61] | Weingarten, V. I. and Seide, P. Elastic stability of thin-walled cylindrical and conical shells under combined external pressure and axial compression. AIAA Journal, 3, 913-920(1965) |
| [62] | Hutchinson, J. W. Imperfection sensitivity of externally pressurized spherical shells. Journal of Applied Mechanics, 34(1), 49-55(1967) |
| [63] | Kirshnamoorthy, G. Buckling of thin cylinders under combined external pressure and axial compression. Journal of Aircraft, 11, 65-68(1974) |
| [64] | Bisagni, C. Numerical analysis and experimental correlation of composite shell buckling and postbuckling. Composites Part B:Engineering, 31(8), 655-667(2000) |
| [65] | Teng, J. G. and Hong, T. Postbuckling analysis of elastic shells of revolution considering mode switching and interaction. International Journal of Solids and Structures, 43(3-4), 551-568(2006) |
| [66] | Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates, Cambridge University Press, Cambridge (2008) |
| [67] | Donnell, L. H. Beam, Plates and Shells, McGraw-Hill, New York (1976) |
| [68] | Vol'mir, A. S. Stability of Elastic Systems, No. FTD-MT-64-335, Foreign Technology Division, Wright-Patterson AFB, Ohio (1965) |
| [69] | Ogata, S., Li, J., and Yip, S. Ideal pure shear strength of aluminum and copper. Science, 298, 807-811(2002) |
| [70] | Zhu, R., Pan, E., Chung, P. W., Cai, X., Liew, K. M., and Buldum, A. Atomistic calculation of elastic moduli in strained silicon. Semiconductor Science and Technology, 21, 906-911(2006) |
| [71] | Prinz, V. Y. and Golod, S. V. Elastic silicon-film-based nanoshells:formation, properties, and applications. Journal of Applied Mechanics and Technical Physics, 47(6), 867-878(2006) |
| [72] | Huang, H. and Han, Q. Nonlinear buckling and postbuckling of heated functionally graded cylindrical shells under combined axial compression and radial pressure. International Journal of Non-Linear Mechanics, 44(2), 209-218(2009) |
 2016, Vol. 37
2016, Vol. 37



