Shanghai University
Article Information
- T. HAYAT, S. MAKHDOOM, M. AWAIS, S. SALEEM, M. M. RASHIDI. 2016.
- Axisymmetric Powell-Eyring fluid flow with convective boundary condition:optimal analysis
- Appl. Math. Mech. -Engl. Ed., 37(7): 919-928
- http://dx.doi.org/10.1007/s10483-016-2093-9
Article History
- Received 2015-11-17;
- in final form 2016-03-08
2. Department of Mathematics, COMSATS Institute of Information Technology, Attock 43600, Pakistan;
3. Department of Mathematics, Statistics and Physics, Qatar University, Doha 2713, Qatar;
4. Shanghai Key Lab of Vehicle Aerodynamics and Vehicle Thermal Management Systems, Tongji University, Shanghai 201804, China
Non-Newtonian fluids in industry and technology are now accepted more appropriate than viscous fluids. Several materials such as polymer solutions or melts, greases, various oils, lubricants, drilling mud, paints, yoghurt, shampoo, and ketchup are classified as non-Newtonian fluids. Apart from thickening and thinning behaviors, other various rheological responses can be seen in the flows of non-Newtonian fluids including normal and tangential stresses and relaxation and retardation time. In view of these characteristics, several empirical and semi-empirical fluid models have been presented in the literature in the past few years. Obviously, all these non-Newtonian fluids due to their immense properties cannot be covered by one mathematical equation. Therefore, many models have been proposed for the description of behavior of the shear thinning/thickening process, the normal stress differences, the stress relaxation, the elastic effects, etc. For-instance, Fetecau et al.[1] presented the time dependent flow of an Oldroyd-B fluid caused by a constantly accelerating plate between two side walls normal to the surface. The authors utilized Fourier-sine transforms and computed the solutions for the Maxwell, secondgrade, and Newtonian fluids. The exact solutions for the rotating flows of a generalized Burgers fluid in a cylindrical system were constructed by Jamil and Fetecau[2]. They used the finite Hankel and Laplace transforms for the solution procedure and presented the computed results in the form of Bessel functions. Hussain et al.[3] explored the oscillatory flows of second-grade fluid in a porous medium. The investigation was presented by the modified Darcy’s law, and the Hall current effects were also analyzed. Akbar[4] presented the impact of magnetic field on the peristaltic flow of a Casson fluid in an asymmetric channel. He explained the application of his work in the crude oil refinement industries. Comprehensive analysis of nano third-grade fluid on a rotating vertical cone was presented by Nadeem and Saleem[5]. Solutions for the momentum, energy, and diffusion equations in the boundary-layer region were presented and analyzed. They used the thermal boundary conditions of the Neumann type on the walls and computed the semi analytical solutions. Sheikholeslami et al.[7] presented the effects of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer for the twophase model. He studied the fourth-order Runge-Kutta method, and the variations of the Reynolds numbers, the rotation effects, the thermophoretic parameter, etc. are analyzed in detail. Thermal convective instability of the viscoelastic fluid in a rotating porous layer heat from below was analyzed by Kang et al.[8]. Coriolis effects on thermal convective instability of viscoelastic fluid in a rotating porous cylindrical annulus were studied by Kang et al.[9]. They incorporated the modified Darcy-Jeffrey model in addition with the Coriolis term to mention the non-viscous rotating rheology in the porous medium. Thermal instability of a nonhomogeneous power law nanofluid in a porous layer with horizontal through flow was investigated by Kang et al.[10]. In this analysis, they considered the power-law model to investigate the shear-thinning behavior. Moreover, the physical quantities including the Lewis number and the Peclet number were analyzed in detail. Unsteady flows of a generalized fractional Burgers’ fluid between two side walls normal to a plate were analyzed by Kang et al.[11]. They computed the exact solution of the momentum equation and presented them of Mittag-Leffler function.
The non-Newtonian fluid flows over a stretching surface have paramount value in polymer industry and electrochemistry. It is generally acknowledged that the stretching of surface might be of several types, i.e., linear and nonlinear stretching, bidirectional stretching, exponential stretching, and radial stretching. In the recent years, various investigators have been engaged in analyzing and predicting the non-Newtonian fluid flow behavior in a boundary layer domain. For-instance, Ahmad et al.[12] presented the effects of thermal radiation on hydromagnetic axisymmetric stagnation point flow and heat transfer of a micropolar fluid about a moving sheet. They presented a detailed study of the hydromagnetic axisymmetric stagnation point flow and heat transfer characteristic of an electrically conducting viscous incompressible micropolar fluid over a shrinking sheet with radiation effects. Sochi[13] investigated the flow of power-law fluids in axisymmetric corrugated tubes. He utilized the analytical method for modelling the relationship between the pressure drop and the flow rate. Khan and Shahzad[14] presented an axisymmetric flow of a Sisko fluid over a radially stretching sheet. They incorporated the twodimensional flow, modeled the problem as a combination of power law and Newtonian fluids, and utilized suitable variables for the simplification of the considered analysis. Hayat et al.[15] analyzed the axisymmetric flow of third-grade fluid between porous disks. The combined effects of magnetic field and heat transfer were considered and analyzed for the axisymmetric fluid flow. Hosseini et al.[16] presented the non-Newtonian fluid flow in an axisymmetric channel with the porous wall. They used the optimal homotopy asymptotic method (OHAM) to construct the solution expressions of momentum and energy equations. A comparison of numerical and analytical solutions was also presented showing validity of the results. Mastroberardino[17] considered the annular axisymmetric stagnation point flow on a moving cylinder and computed the series solutions for the momentum and energy equations. Hydromagnetic axisymmetric third-grade fluid flow between stretching sheets with heat transfer was presented by Hayat et al.[18]. Newtonian heating, thermal-diffusion, and diffusion-thermo effects in an axisymmetric flow of a Jeffrey fluid over a moving surface were presented by Awais et al.[19]. The convergence criterion was presented, and the effects of several important physical quantities were discussed.
In the recent years, investigators have shown interest in minimizing the skin friction coefficient and maximizing the rate of heating/cooling in the rapid and advanced industrial and technological processes. In this direction, serious attempts have been done by considering flows over the surface of a wing, wind turbine rotor, and tail plane. It is noted that the skin friction coefficient can be minimized by taking the boundary layer away from the separation and delay the transition of laminar to turbulent flow. It is achieved via different physical concepts such as by moving the surface and introducing fluid suction and injection. Recently, some investigators have tried to increase the cooling/heating rate by different kinds of physical conditions over a flat surface. Therefore, in this analysis, we investigate the mechanism of boundary layer flow induced by a radially stretching convective wall. The nonlinear equations are mathematically modeled and then solved with the OHAM. The optimized value of convergence control parameter is calculated using the OHAM. References [20]-[27] and the references there in utilized this procedure for the computation of nonlinear problems. Graphical and numerical results are presented to give the real insight of the considered problem.
2 Mathematical formulationThe two-directional axisymmetric flow of a Powell-Eyring fluid is considered. The motion in the fluid is driven by a radially stretching wall located at z = 0, whereas the fluid occupies the region z ≥ 0, as shown in Fig. 1.

|
| Fig. 1 Geometry of flow problem |
The Cauchy stress tensor satisfying the Powell-Eyring fluid model can be stated as

where an extra stress tensor τij for the Powell-Eyring fluid yields
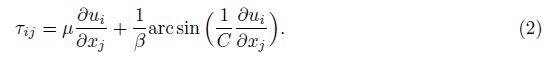
Here, μ represents the dynamic viscosity, p is the pressure, and I is the identity tensor. Moreover, β and C are the material fluid parameters.
By use of the appropriate approximations
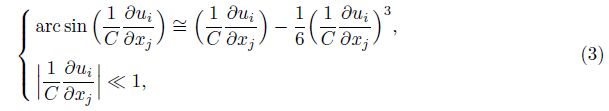
the equations of mass, momentum, and energy under boundary layer approximations give

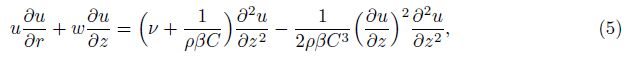

where the momentum and thermal boundary conditions are in the forms of
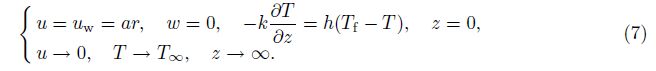
uw is the velocity at the wall, r is the radial direction, ν = μ/ρ is the kinematic viscosity, ρ is the fluid density, σ is the thermal diffusivity, a is the dimensional constant related to the rate of radially stretching sheet, h is the heat transfer coefficient, k is the thermal conductivity, T is the fluid temperature, and Tf is the temperature of hot fluid.
By utilizing the following variables:
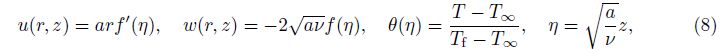
the incompressibility (4) satisfies identically, where the laws of conservation of momentum and energy (5) and (6) become
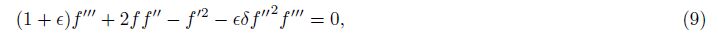

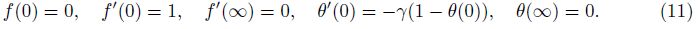
In the above equations, γ represents the Biot number, Pr is the Prandtl number, and ε and δ are the fluid parameters. They are defined as
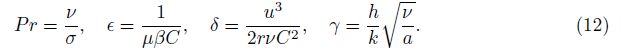
The skin friction coefficient Cf is given by
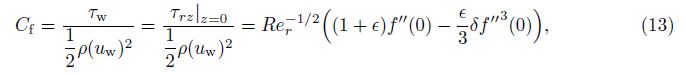
and the local Nusselt number Nur is given by
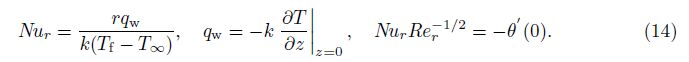
We select the initial guesses in the forms of
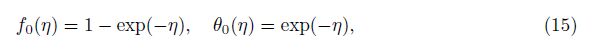
where the auxiliary linear operators are given by


Now, (9) and (10) are subjected to the physical conditions (11) using the homotopy analysis
method (HAM)[20, 21, 22, 23, 24, 25, 26, 27]. We select  and
and  as the auxiliary parameters for the functions f
and θ, respectively. The convergence of derived series solutions can be adjusted and controlled
through these auxiliary parameters. The
as the auxiliary parameters for the functions f
and θ, respectively. The convergence of derived series solutions can be adjusted and controlled
through these auxiliary parameters. The  -curves for f´´(0) and θ´(0) are sketched at the 15th
iteration in Fig. 2. This plot depicts that the domains of suitable region of
-curves for f´´(0) and θ´(0) are sketched at the 15th
iteration in Fig. 2. This plot depicts that the domains of suitable region of  and
and  are -0.9
≤
are -0.9
≤  ≤ -0.25 and -1.35 ≤
≤ -0.25 and -1.35 ≤  ≤ -0.15, respectively.
≤ -0.15, respectively.

|
Fig. 2  -curves for f´´(0) and θ´(0) when γ = 0.8, δ = 0.1, and ε = Pr = 1.0 -curves for f´´(0) and θ´(0) when γ = 0.8, δ = 0.1, and ε = Pr = 1.0
|
The homotopy series solution contains the non-zero auxiliary parameters c0f and c0θ , which is in fact the range of convergence of the homotopy solutions. To get the optimized values of c0f and c0θ, we use the idea of minimization by defining the squared average residual errors,
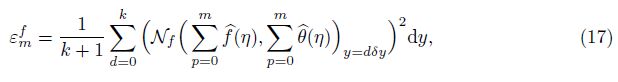
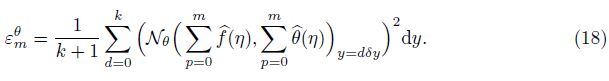
Following Liao[20],

where the total squared residual error is εmt . δy = 0.5, and k = 20. Table 1 is arranged to show the minimized values of total averaged-squared residual error for the group of optimized convergence control parameters at various iterations.
 |
Both residual errors are given in Table 2 at various iterations against the 8th-order optimal convergence control parameters. It is perceived that both the residual errors decrease with the increasing iterations.
 |
The aim of this portion of the manuscript is to present the influence of several physical quantities on the velocity and temperature profiles. Therefore, we prepare Figs. 3-7. Figure 3 presents the comparison of the Newtonian and Powell-Eyring fluid models. It is observed that the magnitude of velocity is greater for the Powell-Eyring fluid model when compared with the Newtonian model.

|
| Fig. 3 Newtonian modle vs. Powell-Eyring model |

|
| Fig. 4 Effects of ε on f ´ |

|
| Fig. 5 Effects of ε on θ |

|
| Fig. 6 Effects of γ on θ |

|
| Fig. 7 Effects of Pr on θ |
It is because of the fact that the Powell-Eyring fluid is a shear thinning fluid, in which the viscosity decreases with the shear rate which results in an increase of the fluid velocity, as observed in Fig. 3. The impact of the fluid parameter against the velocity profile is shown in Fig. 4.
It is noteworthy that the velocity profile depicts an increment with the increasing ε . Furthermore, the boundary layer is thicker for larger values of the fluid parameter ε . In real, larger values of ε result in the reduction of fluid viscosity because of the shear thinning property of the fluid, which enhances the molecular movement and results into increase of the velocity field. The behavior of ε on the temperature is shown in Fig. 5. This figure shows that the temperature profile and the thickness of thermal boundary layer reduce when is increased. Physically, it justifies that higher values of ε produce a reduction in the fluid viscosity. Therefore, less heat is produced due to frictional forces. Hence, the temperature distribution decreases.
Figure 6 shows the behavior of the Biot number γ on the temperature field. It is perceived that there is an increase of temperature for large Biot numbers γ.
It is due to fact that as we increase the Biot number, the heat transfer coefficient also increases, which is responsible in enhancement of temperature profile. Moreover, an increase of the Biot number also causes a thermal slip at the wall. The behavior of Pr on the temperature is sketched in Fig. 7. It is obvious that the temperature of fluid decreases with Pr. Moreover, the thermal boundary layer is thicker for smaller Pr. The Prandtl number is the ratio of momentum and thermal diffusivities. Therefore, large Prandtl numbers result in the reduction of thermal diffusivity. Therefore, the temperature profile decreases.
Numerical behaviors of the skin friction coefficient and the local Nusselt number for important parameters are deliberated in Tables 3 and 4. It is obvious from Table 3 that the skin friction coefficient enhances by increasing ε , while it decreases when increase δ. Thus, higher values of δ can be used for the reduction of the skin friction coefficient in different industrial processes in order to increase the efficiency of various machines. Table 4 shows that the value of the local Nusselt number increases for increasing values of Pr, γ, and ε , and it decreases by increasing δ. It is analyzed that higher values of Pr, γ, and ε can be used as cooling agent in various industrial and technological processes in order to avoid over heating of machines. Table 5 shows the comparison of Nusselt number with the previous published material. It is concluded that both the results are in reasonable relation.
The axisymmetric flow induced by a radially stretching sheet with convective boundary conditions is discussed. The major findings are given below.
(i) The magnitude of velocity is greater for the Powell-Eyring fluid as compared with that of the viscous fluid.
(ii) Larger values of enhance the velocity profile.
(iii) The temperature profile decreases due to an increase of ε .
(iv) The Biot number enhances the wall temperature and produces the thermal slip.
(v) The thermal boundary layer is thicker for larger values of γ.
We hope that the present investigation serves as a stimulus for stretching flows especially in polymeric sheets, annealing, and thinning of copper wires and food processes. The performed study may be extended for the subclass of non-Newtonian fluids describing relaxation and retardation time characteristics. The presented analysis can also be modeled for the flows of nanofluid with various physical aspects.
AcknowledgementsWe are grateful to the editor and the referees for their valuable suggestions.
| [1] | Fetecau, C., Nazar, M., and Fetecau, C. Unsteady flow of an Oldroyd-B fluid generated by a constantly accelerating plate between two-side walls perpendicular to the plate. Internationl Journal of Nonlinear Mechanics, 44, 1039-1047(2009) |
| [2] | Jamil, M. and Fetecau, C. Some exact solutions for rotating flows of a generalized Burgers' fluid in cylindrical domains. Journal of Non-Newtonian Fluid Mechanics, 165, 1700-1712(2010) |
| [3] | Hussain, M., Hayat, T., Asghar, S., and Fetecau, C. Oscillatory flows of second grade fluid in a porous space. Nonlinear Analysis:Real World Applications, 11, 2403-2414(2010) |
| [4] | Akbar, N. S. Influence of magnetic field on peristaltic flow of a Casson fluid in an asymmetric channel:application in crude oil refinement. Journal of Magnetism and Magnetic Materials, 378, 463-468(2015) |
| [5] | Nadeem, S. and Saleem, S. Analytical study of third grade fluid over a rotating vertical cone in the presence of nanoparticles. Internationl Journal of Heat and Mass Transfer, 85, 1041-1048(2015) |
| [6] | Alloui, Z. and Vasseur, P. Natural convection of Carreau-Yasuda non-Newtonian fluids in a vertical cavity heated from sides. Internationl Journal of Heat and Mass Transfer, 84, 912-924(2015) |
| [7] | Sheikholeslami, M., Ganji, D. D., Javed, M. Y., and Ellahi, R. Effects of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two-phase model. Journal of Magnetism and Magnetic Materials, 374, 36-43(2015) |
| [8] | Kang, J., Fu, C., and Tan, W. C. Thermal convective instability of viscoelastic fluids in a rotating porous layer heated from below. Journal of Non-Newtonian Fluid Mechanics, 166, 93-101(2011) |
| [9] | Kang, J., Niu, J., Fu, C., and Tan, W. C. Coriolis effect on thermal convective instability of viscoelastic fluids in a rotating porous cylindrical annulus. Transport in Porous Media, 98, 349-362(2013) |
| [10] | Kang, J., Zhou, F., Tan, W. C., and Xia, T. Thermal instability of a nonhomogeneous powerlaw nanofluid in a porous layer with horizontal through flow. Journal of Non-Newtonian Fluid Mechanics, 213, 50-56(2014) |
| [11] | Kang, J., Liu, Y., and Xia, T. Unsteady flows of a generalized fractional Burgers' fluid between two-side walls perpendicular to a plate. Advances in Mathematics and Physics, 2015, 521069(2015) |
| [12] | Ahmad, S., Ashraf, M., and Syed, K. S. Effects of thermal radiation on MHD axisymmetric stagnation point flow and heat transfer of a micropolar fluid over a shrinking sheet. World Applications Science Journal, 15, 835-848(2011) |
| [13] | Sochi, T. The flow of power-law fluids in axisymmetric corrugated tubes. Journal of Peterolium and Science Engineering, 78, 582-585(2011) |
| [14] | Khan, M. and Shahzad, A. On axisymmetric flow of Sisko fluid over a radially stretching sheet. International Journal of Nonlinear Mechanics, 47, 999-1007(2012) |
| [15] | Hayat, T., Shafiq, A., Nawaz, M., and Alsaedi, A. MHD axisymmetric flow of third grade fluid between porous disks with heat transfer. Applied Mathematics and Mechanics (English Edition), 33(6), 749-764(2012) DOI 10.1007/s10483-012-1584-9 |
| [16] | Hosseini, Z., Sheikholeslami, M., and Ganji, D. D. Non-Newtonian fluid flow in an axisymmetric channel with porous wall. Propulsion and Power Research, 2, 254-262(2013) |
| [17] | Mastroberardino, A. Series solutions of annular axisymmetric stagnation flow and heat transfer on moving cylinder. Applied Mathematics and Mechanics (English Edition), 34(9), 1043-1054(2013) DOI 10.1007/s10483-013-1726-7 |
| [18] | Hayat, T., Shafiq, A., Alsaedi, A., and Awais, M. MHD axisymmetric flow of third grade fluid between stretching sheets with heat transfer. Computors and Fluids, 86, 103-108(2013) |
| [19] | Awais, M., Hayat, T., Nawaz, M., and Alsaedi, A. Newtonian heating, thermal-diffusion and diffusion-thermo effects in an axisymmetric flow of a Jeffrey fluid over a stretching sheet. Brazilien Journal of Chemical Enginerring, 32, 555-561(2015) |
| [20] | Liao, S. J. An optimal homotopy analysis method approach for strongly nonlinear differential equation. Communication in Nonlinear Science and Numerical Simulations, 15, 2003-2016(2010) |
| [21] | Rashidi, M. M. and Pour, S. A. M. Analytic approximate solutions for unsteady boundary-layer flow and heat transfer due to a stretching sheet by homotopy analysis method. Nonlinear Analysis:Modelling and Control, 15, 83-95(2010) |
| [22] | Rashidi, M. M., Freidoonimehr, N., Hosseini, A., Beg, O. A., and Hung, T. K. Homotopy simulation of nanofluid dynamics from a non-linearly stretching isothermal permeable sheet with transpiration. Meccanica, 49, 469-482(2014) |
| [23] | Abbasbandy, S. and Hayat, T. On series solution for unsteady boundary layer equations in a special third grade fluid. Communication in Nonlinear Science and Numerical Simulations, 16, 3140-3146(2011) |
| [24] | Awais, M., Hayat, T., Irum, S., and Alsaedi, A. Heat generation/absorption effects in a boundary layer stretched flow of Maxwell nanofluid:analytic and numeric solutions. Plos One, 10, e0129814(2015) |
| [25] | Hayat, T., Ali, S., Awais, M., and Alhuthali, M. S. Newtonian heating in stagnation point flow of Burgers fluid. Applied Mathematics and Mechanics (English Edition), 36(1), 61-68(2015) DOI 10.1007/s10483-015-1895-9 |
| [26] | Wang, C. Y. Natural convection on a vertical radially stretching sheet. Journal of Mathematical Analysis and Applications, 332, 877-883(2007) |
| [27] | Asad, S., Alsaedi, A., and Hayat, T. Flow of couple stress fluid with variable thermal conductivity. Applied Mathematics and Mechanics (English Edition), 37(3), 315-324(2016) DOI 10.1007/s10483-016-2031-6 |
 2016, Vol. 37
2016, Vol. 37





