Shanghai University
Article Information
- Luyu SHEN, Changgen LU. 2016.
- Local receptivity in non-parallel boundary layer
- Appl. Math. Mech. -Engl. Ed., 37(7): 929-940
- http://dx.doi.org/10.1007/s10483-016-2092-9
Article History
- Received 2015-10-19;
- in final form 2015-12-25
2. School of Marine Science, Nanjing University of Information Science and Technology, Nanjing 210044, China
The mechanism of the laminar-turbulent transition in fluid mechanic has attracted scholars’ interest all the time. The transition process is generally divided into the stages: receptivity, growth with the linear stability theory (LST), nonlinear evolution, and breakdown into the turbulent flow. Recently, a lot of relevant studies on the laminar-turbulent transition have been carried out[1, 2, 3]. However, these works all ignored the effect of the initial stage in the transition process. Receptivity, which establishes the initial conditions of amplitudes, frequencies, wave numbers, and phases of the unstable waves, plays an important role in the laminar-turbulent transition[4].
Up to now, it has been acknowledged that the boundary layer is receptive to acoustic waves or vortical disturbances interacting with small perturbation in the boundary layer (such as the localized wall roughness, the wall suction and blowing, and the leading edge effect) which excites the unstable Tollmien-Schlichting (T-S) waves. Earlier, the acoustic local receptivity mechanism was explained by Goldstein[5, 6] and Ruban[7] independently using the triple-deck formulation. This receptivity mechanism was verified by a series of experiments such as Saric et al.[8], Wiegel and Wlezien[9], and W¨urz et al.[10]. Then, Choudhari[11] and Duck et al.[12] revealed the local boundary-layer receptivity mechanism to vortical disturbances in the free stream by the finite-Reynolds number approach and the matched asymptotic method, respectively. This receptivity mechanism was first confirmed by the experiments of Dietz[13, 14, 15] that the excited unstable T-S waves were observed in the boundary layer. A perfect quantitative agreement with Dietz's experimental results was made by Wu[16, 17], who presented a secondorder asymptotic theory based on the triple-deck formulation. On this basis, Zhang and Zhou[18] and Shen and Lu[19] performed direct numerical simulation (DNS) of the local boundary-layer receptivity to vortical disturbances, but their results limited to applying the periodic boundary condition in the streamwise direction. Then, the finite-Reynolds number approach was adopted by Ricco[20] to research the local boundary-layer receptivity induced by gusts with small normal wavelength, which was also based on the parallel flow assumption. The relation between the receptivity efficiency function and the wavelength of the vortical disturbances in the free stream was determined. Zuccher and Luchini[21] introduced the multiple scale method to compare the parallel and non-parallel results of local boundary-layer receptivity and found that the maximum difference in the amplitude of the parallel and non-parallel receptivity coefficients was on the order of 10%-15%.
In our research, to overcome the disadvantages of the parallel flow assumption in the previous studies[18, 19, 20] and make more conform to the natural laminar-turbulent transition, the Navier- Stokes equations are solved numerically to obtain the basic flow in the non-parallel flat-plate boundary layer. Additionally, considering that turbulence is ubiquitous in the free stream, we extend single vortical disturbances to the free-stream turbulence (FST) for the study of local boundary-layer receptivity. The difference between the non-parallel and parallel boundary layers on the local receptivity is investigated. What is more important by comparing with Refs. [18] and [19] is that we study the relation between the local receptivity in the boundary layer and the frequency of the FST as well as the effects of the multiple localized roughness and the roughness location on the local receptivity in the boundary layer. High-order and highresolution compact finite difference schemes on non-uniform meshes are utilized to perform the DNS of local boundary-layer receptivity to the FST interacting with localized wall roughness, and some meaningful results are achieved.
2 Fundamental equations and computing methods 2.1 Fundamental equationsThe dimensionless perturbation equations deduced from the Navier-Stokes equations are
Here, U = [U, V]T is the basic flow in the non-parallel flat-plat boundary layer obtained by solving the Navier-Stokes equations, where U and V are the velocity components in the xdirection and the y-direction of the basic flow, respectively, u = [u, v]T is the perturbation velocity, and p is the perturbation pressure. The Reynolds number Re = (U∞δ∗)/ν, where δ∗ is the boundary-layer displacement thickness, U∞ is the free-stream velocity, and ν is the kinematic viscosity.High-order finite difference schemes are utilized to discretize the fundamental equations. A modified fourth-order Runge-Kutta scheme is used for time integration[22]. The compact finite difference schemes on non-uniform meshes are applied for spatial discretization[23]. The convective terms are discretized by the fifth-order upwind compact scheme. The pressure gradient terms are discretized by the sixth-order compact scheme. The viscosity terms are discretized by the fifth-order compact scheme. Besides, the pressure Poisson equation is solved by the fourth-order schemes on the non-uniform meshes. The details for the discrete schemes can be seen in Ref. [23].
2.2 FST modelThe mathematical model[24] is introduced to generate the FST, which is given by
in which Here,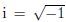 denotes the amplitude, κ1 and κ2 are the fundamental wave numbers in the x-direction and y-direction, respectively, and κ1 is also the fundamental frequency, the frequency ω = mκ1, and the streamwise and normal wave numbers are α = mκ1 and β = jκ2, respectively. κ = (α2 + β2)1/2. M and J are the selected maximum mode numbers. The velocity spectrum
denotes the amplitude, κ1 and κ2 are the fundamental wave numbers in the x-direction and y-direction, respectively, and κ1 is also the fundamental frequency, the frequency ω = mκ1, and the streamwise and normal wave numbers are α = mκ1 and β = jκ2, respectively. κ = (α2 + β2)1/2. M and J are the selected maximum mode numbers. The velocity spectrum  and
and  depend on the one-dimensional energy spectrum E(κ) and the random angle θ .
2.3 DNS domain
depend on the one-dimensional energy spectrum E(κ) and the random angle θ .
2.3 DNS domain The computational domain of the DNS is shown in Fig. 1. The length of the domain is X = 2.0 × 2π/κ1, and the height of the domain is Y = 14.39, which is five times of the boundary layer thickness so that there is sufficient space for the evolution of the excited waves in the boundary layer. The computational domain is x ∈ [0, X] and y ∈ [0, Y]. The roughness element is placed at the location [x1, x2], where x1 is the start location, and x2 is the end location on the flat-plate. L = x2 − x1, and L is the roughness length.

|
| Fig. 1 DNS domain |
The computational grids are uniform in the x-direction and concentrated near the wall in the y-direction to improve the resolution where flow is rapidly varying in the near-wall region. Three sets of grids (512 × 150, 1 024× 200, and 2 048× 250) are adopted to test the grid convergence at the Reynolds number 1 000. By comparing the numerical results of the dispersion relations of T-S waves with the LST, the absolute errors for three sets of grids are on the order of 10-4, 10-5, and 10-5, respectively. Therefore, the optimal converged grid is implied to be 1 024×200.
2.4 Boundary conditions(i) The upper boundary
The pressure is set to zero, and accordingly, the perturbation velocity of the imposed FST[24] is
(ii) The lower boundary
The no-slip wall conditions are utilized, i.e., u(x, 0) = 0, v(x,0) = 0, and  = 0. The rectangle localized roughness elements are added on the flat-plate,
= 0. The rectangle localized roughness elements are added on the flat-plate,
(iii) The inflow boundary The perturbation velocity is determined by the FST model as well, and  = 0.
= 0.
(iv) The outflow boundary
 = 0, and the non-reflect boundary condition[21] is given by
= 0, and the non-reflect boundary condition[21] is given by
To compare with Dietz's experiments[15], a non-dimensional frequency is defined as F = 2πfν/U∞ × 106[15, 19], the inflow Reynolds number Re is set to 1 000, a rectangle roughness element is placed at the location x1 = 40 and x2 = 70, the roughness length is L = 30.0, and the height is h∗/δr = 0.20, where h∗ is the dimensional height, and δr = (νx/U∞)1/2 is the boundary-layer reference height. The fundamental wave number of the imposed FST is κ1 = 0.01, and the maximum mode number is M = 8.
Under these conditions, the DNS of local boundary-layer receptivity to the FST is carried out. As a result, a group of generated perturbation wave packets are observed in the boundary layer, which is determined by a subtraction of the result computed above a smooth plate from a similar result with a wall roughness element. Figure 2 gives the spatial evolution of streamwise velocity in the boundary layer. As shown in Fig. 2, the amplitude of the wave packets is gradually amplifying in the streamwise direction. According to these spatial evolutions, the positions of peaks and valleys of the wave packets are tracked over time to estimate the propagation speed of the wave packets which is 0.325. It is very close to the propagation speed of the T-S wave packets measured by Dietz[14], one-third of the free-stream velocity. In this section below, further verification is presented to prove that the generated perturbation wave packets are real T-S wave packets via the comparisons of the numerical results of the dispersion relations, the phase speed, the growth rate, the amplitude, and the phase of the perturbation waves with the experiment data and the LST.

|
| Fig. 2 Spatial evolution of wave packets excited by FST interacting with localized wall roughness |
Firstly, a group of perturbation waves with different frequencies are separated from the perturbation wave packets in Fig. 2 by the fast Fourier transform, as shown in Fig. 3. Figures 3(a) and 3(b) give the spatial evolutions of the stable and unstable perturbation waves, respectively. It is found that the excited perturbation waves of F < 46 are all stable waves, and those of 46 < F < 116 are all unstable ones, which accords with the theoretical solutions of the neutral stability curve.

|
| Fig. 3 Spatial evolutions of perturbation waves with different frequencies separated from wave packets |
Secondly, according to these spatial evolutions of perturbation waves at different times, the positions of wave peaks and valleys are recorded over time to calculate the average wave number and the average phase speeds. The obtained results are shown in Table 1. Table 1 shows that the generated perturbation waves in the boundary layer have the same frequencies but shorter wavelengths (or larger wave numbers) by comparing with the imposed FST. These results conform to the wavelength conversion mechanism for the local boundary-layer receptivity. Moreover, the dispersion relations of the excited perturbation waves are in accordance with those of T-S waves obtained from the LST. Meanwhile, the phase speeds of the perturbation waves with different frequencies agree well with the solutions of the LST, and the phase speed of F = 50 is very close to the phase speed of T-S wave measured by Dietz[15].
 |
Thirdly, the growth rates of the excited perturbation waves are computed and compared with the results of the eN method and Dietz's measurements[15]. The streamwise growths of T-S wave amplitudes with different frequencies computed by the eN method are
Here, the Reynolds number is defined as R =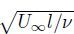 , where l is the distance to the leading edge of the flat-plate. Rr is the Reynolds number of the roughness location, and the N-factors are calculated by integrating the growth rate αi which are obtained from the LST. The wave amplitude |u| is normalized by the amplitude at the roughness location |ur| in Fig. 4. Figure 4 shows that the numerical results of the streamwise growths of perturbation wave amplitudes with different frequencies are in agreement with the results of the LST, and the streamwise growth of F = 50 is also found to be in accordance with Dietz's measurements[15]. Thus, it can be inferred that the growth rates of the perturbation waves are in accordance with those of the LST and agree well with Dietz's measurements[15] for the case of F = 50.
, where l is the distance to the leading edge of the flat-plate. Rr is the Reynolds number of the roughness location, and the N-factors are calculated by integrating the growth rate αi which are obtained from the LST. The wave amplitude |u| is normalized by the amplitude at the roughness location |ur| in Fig. 4. Figure 4 shows that the numerical results of the streamwise growths of perturbation wave amplitudes with different frequencies are in agreement with the results of the LST, and the streamwise growth of F = 50 is also found to be in accordance with Dietz's measurements[15]. Thus, it can be inferred that the growth rates of the perturbation waves are in accordance with those of the LST and agree well with Dietz's measurements[15] for the case of F = 50.

|
| Fig. 4 Numerical results of streamwise growths of T-S wave amplitudes compared with results of eN method and Dietz's measurements[15] (F = 50) |
Finally, for the further verification of local boundary-layer receptivity, one of the excited perturbation waves is selected from Table 1 whose frequency F = 50 is the same as that measured by Dietz[15]. Figure 5 gives the numerical results of the amplitude and phase vertical profiles of streamwise perturbation velocity of this wave comparing with the solutions of the LST and Dietz's measurements[15]. The results coincide completely.

|
| Fig. 5 Numerical results of amplitude and phase vertical profiles of excited perturbation wave compared with solutions of LST and Dietz's measurements[15] |
From the above, the numerical results of the frequency, the wave number, the phase speed, the growth rate, the amplitude, and the phase of the excited perturbation waves all agree well with the theoretical solutions of T-S waves obtained from the LST and Dietz's measurements[15].Therefore, the excited perturbation wave packets in the boundary layer are confirmed to be T-S wave packets superposed by a group of stable and unstable T-S waves under interaction of the FST and localized wall roughness. Consequently, it demonstrates that the local boundary-layer receptivity does exist.
3.2 Receptivity responses to amplitude of FST, roughness height, and roughnesslength The local boundary-layer receptivity is verified to be linear within a specific range for the case of vortical disturbances interacting with the localized wall roughness[15, 16, 18], which is given by
Here, uTS is the T-S wave amplitude at the roughness location, uFS is the forcing amplitude, and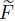 (αTS − αFS) is the spatial transform of the roughness geometry at the wave number of difference between the T-S wave number αTS and the wave number of free-stream disturbance αFS. The efficiency function Λ is independent of the roughness geometry.
(αTS − αFS) is the spatial transform of the roughness geometry at the wave number of difference between the T-S wave number αTS and the wave number of free-stream disturbance αFS. The efficiency function Λ is independent of the roughness geometry.
In this section, the amplitudes of FST, roughness heights, and roughness lengths are varied to determine the relation of local receptivity with the amplitudes of the FST, with the roughness heights, and with the roughness lengths for the case of FST interacting with the localized wall roughness. To facilitate the comparison with Dietz's experiments[15], T-S wave amplitudes at the roughness location |u| are normalized by the T-S wave amplitudes |u0| excited under the condition of uFST = 0.3%, L = 30.0, and h∗/δr = 0.20, where uFST is the amplitude of the imposed FST at the edge of the boundary layer, η ≡ y∗/(2x∗ν/U∞)1/2 = 8 and R = 630 at a fixed streamwise location.
Figure 6 (a) gives the variations of the excited T-S wave amplitudes with the amplitude of the imposed FST at the edge of the boundary layer uFST. The local boundary-layer receptivity is linear for uFST up to 1% of the free-stream velocity. Figure 6 (b) shows that for the height h∗/δr less than 0.2, the receptivity responses of the T-S waves with different frequencies are all linear. When the height h∗/δr is greater than 0.2, the receptivity responses turn to be a nonlinear increase. These conclusions are in good agreement with Dietz's experiment[15] and the numerical results[18, 19] for the vortical receptivity, and are also similar to those for the acoustic receptivity[8, 25, 26].

|
|
Fig. 6 Numerical results of T-S wave amplitudes varying with amplitudes of FST uFST and with roughness heights h |
Moreover, the spatial Fourier transform of a single rectangle hump evaluated at αTS − αFS is given by
Figure 7 (a) gives the variations of T-S wave amplitudes with the roughness lengths, where L is normalized by the resonant wave length 2π/(αTS −αFS) (αTS = 0.128 11, αFS = 0.040 00 for F = 40; αTS = 0.154 78, αFS = 0.050 00 for F = 50; and αTS = 0.180 52, αFS = 0.060 00 for F = 60, see Table 1), and the T-S wave amplitudes |u| are normalized by the maximum amplitudes |umax|. As seen in Fig. 7 (a), the T-S wave amplitude variations with the roughness lengths coincide with the function sin(L(αTS − αFS)/2) in Eq. (8). The T-S wave amplitudes increase initially with the roughness lengths and reach a maximum when the roughness lengths are equal to π/(αTS − αFS). Then, they decrease as the roughness lengths increase when the roughness lengths are greater than π/(αTS − αFS). Figure 7 (b) shows that the receptivity response is almost linear with the spatial Fourier transform of the roughness geometry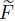 (αTS − αFS). These results reach the same conclusions with Dietz's experiments[15] and Zhang and Zhou’s simulation[18].
(αTS − αFS). These results reach the same conclusions with Dietz's experiments[15] and Zhang and Zhou’s simulation[18].

|
Fig. 7Numerical results of T-S wave amplitudes varying with normalized roughness lengths L(αTS−αFS)/(2π) and with Fourier transform of roughness geometry 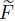 (αTS − αFS) compared with Dietz's measurements[15]
(αTS − αFS) compared with Dietz's measurements[15]
|
The effects of the disturbance frequency, the roughness location, and the numbers of multiple roughness elements on the local receptivity are studied in this section. To facilitate the comparison with Dietz's experiments[15] and Wu's calculations[16], the amplitude of FST at the edge of the boundary-layer uFST is equal to 0.3%, the roughness height is h∗/δr = 0.20, and the roughness length is L = 30.0. The receptivity coefficient Λ is calculated by Eq. (7).
Firstly, we study the relation between the receptivity coefficient Λ and the disturbance frequency F at a fixed localized roughness R = 620. Figure 8 shows that the numerical result of receptivity coefficient decreases slightly as the disturbance frequency of the FST F increases. It agrees well with the receptivity coefficient measured by Dietz[15] and calculated by Wu[16].

|
| Fig. 8 Receptivity coefficient Λ varying with localized roughness location R |
Then, the relation between the receptivity coefficient Λ and the roughness location is also studied. As seen in Fig. 9 (a), within the range of 350 < R < 850, the receptivity coefficient gradually decreases as the roughness is moved downstream, whereas the receptivity coefficient increases as the roughness is moved upstream. That is, the roughness elements located closer to the leading edge of the flat-plate induce more strong receptivity. These results are in agreement with Dietz's measurements[15] and Wu's theoretical calculation[16]. Figure 9 (b) gives the variation of parallel and non-parallel receptivity coefficients with the roughness location. The numerical results demonstrate that when the Reynolds number R is less than 650, the receptivity coefficients considering the effect of non-parallel boundary layer are stronger than those based on the parallel assumption. The maximum difference between the parallel and non-parallel receptivity coefficients is about 10%. It is in accordance with the results computed by Zuccher and Luchini[21]. When the Reynolds number R is greater than 650, the difference between the parallel and non-parallel receptivity coefficients is very small. Therefore, the parallel flow assumption is available for the local boundary-layer receptivity at large Reynolds numbers[27]. In addition, Fig. 9 shows that for different disturbance frequencies, the receptivity coefficient variations with the roughness location have the similar trends.

|
| Fig. 9 Receptivity coefficient Λ varying with localized roughness location R |
Finally, we research the variation of T-S wave amplitudes |u| with the numbers of rectangle roughness elements n (n = 1, 3, 5, 7, 9, and 11), which are normalized by the amplitude of T-S wave excited by a single roughness |un=1| as shown in Fig. 10. Since T-S waves with different frequencies have different T-S wave numbers αTS and wave numbers of free-stream disturbance αFS, the resonant spaces of multiple localized roughness elements 2π/(αTS − αFS) are not the same. The roughness elements are distributed evenly and spaced to give the resonant wave numbers for the T-S wave of F = 50, i.e., αTS = 0.154 78 and αFS = 0.050 00. At these wave numbers, the amplitude of T-S wave increases linearly with the numbers of the roughness elements up to five roughness elements; beyond five roughness elements, the increase turns to be slower; and the increase in receptivity saturates as the roughness elements number n is equal to or greater than nine. However, the spaces of these roughness elements do not satisfy the resonance condition of T-S waves with F = 40 and F = 60, respectively. Hence, their amplitude increases are not so obvious at the F = 50 case. Furthermore, if the T-S waves with different frequencies satisfy their own resonant conditions, the increase of the T-S wave amplitude with the numbers of roughness elements is similar to the case of F = 50. Otherwise, the increase is not so obvious as the resonant case. These results are consistent with Dietz's measurements[15] and Wu's theoretical calculation[16].
High-order and high-resolution compact finite difference schemes on non-uniform meshes are utilized to perform the DNS of the local boundary-layer receptivity to the FST interacting with the localized wall roughness, and the conclusions are summarized as follows.
(i) The perturbation wave packets excited in the boundary layer by the FST interacting with the localized wall roughness are confirmed to be T-S wave packets superposed by a group of stable and unstable T-S waves, and the propagation speed of the T-S wave packets is approximate to 0.325. The numerical results of the dispersion relation, the growth rate, the phase speed, the amplitude, and the phase of the excited perturbation waves all agree well with the solutions of the LST and Dietz's measurements[14, 15]. Thus, it fully demonstrates the existence of local boundary-layer receptivity.
(ii) The amplitudes of excited T-S waves with different frequencies are found to be linear for the amplitude of FST at the edge of the boundary layer uFST up to 1% of the free-stream velocity. When the non-dimensional height h∗/δr is less/greater than 0.2, the local boundarylayer receptivity responses is a linear/nonlinear increase. The variations of T-S wave amplitudes with the normalized roughness length L(αTS − αFS)/2 are in agreement with the function sin(L(αTS − αFS)/2). When the roughness length is equal to π/(αTS − αFS), the maximum amplitude of T-S wave is achieved. The receptivity response is almost linear with the spatial Fourier transform of the roughness geometry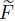 (αTS − αFS).
(αTS − αFS).
(iii) The receptivity coefficient Λ decreases as the disturbance frequency F increases. The roughness elements positioned closer to the leading edge of the flat-plate can induce more strong receptivity. If the multiple roughness elements are spaced to satisfy the resonance condition for the T-S wave with F = 50, the T-S wave amplitude with F = 50 increases linearly with the number of the roughness elements up to five roughness elements. Beyond five roughness elements, the increase turns to be slower and approaches an upper limit as the roughness elements number n reaches nine. The spaces of these roughness elements do not satisfy the resonance condition of T-S waves with F = 40 and F = 60, respectively. Hence, their amplitude increases are not so obvious at the F = 50 case. These results reach the same conclusions as Dietz's measurements[15] and Wu's theoretical calculations[16].
(iv) The non-parallel receptivity coefficient is larger than the parallel receptivity coefficient when the Reynolds number is less than 650. The maximum difference between the non-parallel and parallel receptivity coefficients is about 10%, which is in accordance with Zuccher and Luchini’s result[21]. When the Reynolds number is greater than 650, there is a slight difference between the parallel and non-parallel receptivity coefficients. Thus, the parallel flow assumption is available for the local boundary-layer receptivity at large Reynolds numbers.
| [1] | Chen, L., Tang, D. B., and Liu, C. Numerical studies on evolution of secondary streamwise vortices in transitional boundary layers. Advances in Applied Mathematics and Mechanics, 32, 449-458(2011) |
| [2] | Wu, W. Z. and Tang, D. B. Studies on nonlinear stability of three-dimensional H-type disturbance. Acta Mechanica Sinica, 19, 517-526(2003) |
| [3] | Zheng, X. B. and Jiang, N. The spatial-temporal evolution of coherent structures in log law region of turbulent boundary layer. Acta Mechanica Sinica, 31, 16-24(2015) |
| [4] | Saric, W. S., Reed, H. L., and Kerschen, E. J. Boundary-layer receptivity to freestream disturbances. Annual Review of Fluid Mechanics, 34, 291-319(2002) |
| [5] | Goldstein, M. E. The evolution of Tollmien-Schlichting waves near a leading edge. Journal of Fluid Mechanics, 127, 59-81(1983) |
| [6] | Goldstein, M. E. Scattering of acoustic waves into Tollmien-Schlichting waves by small streamwise variations in surface geometry. Journal of Fluid Mechanics, 154, 509-529(1985) |
| [7] | Ruban, A. I. On the generation of Tollmien-Schlichting waves by sound. Fluid Dynamics, 19, 709-717(1984) |
| [8] | Saric, W. S., Hoos, J. A., and Radeztsky, R. H. Boundary-layer receptivity of sound with roughness. Boundary Layer Stability and Transition to Turbulence, 1, 17-22(1991) |
| [9] | Wiegel, M. and Wlezien, R. Acoustic receptivity of laminar boundary layers over wavy walls. The 3rd Shear Flow Conference, American Institute of Aeronautics and Astronautics, Reston (1993) |
| [10] | Würz, W., Herr, S., Wörner, A., Rist, U., Wagner, S., and Kachanov, Y. S. Three-dimensional acoustic-roughness receptivity of a boundary layer on an airfoil:experiment and direct numerical simulations. Journal of Fluid Mechanics, 478, 135-163(2003) |
| [11] | Choudhari, M. Boundary-layer receptivity to three-dimensional unsteady vortical disturbances in free stream. The 34th Aerospace Sciences Meeting and Exhibit, American Institute of Aeronautics and Astronautics, Reston (1996) |
| [12] | Duck, P. W., Ruban, A. I., and Zhikharev, C. N. The generation of Tollmien-Schlichting waves by free-stream turbulence. Journal of Fluid Mechanics, 312, 341-371(1996) |
| [13] | Dietz, A. J. Distributed boundary layer receptivity to convected vorticity. Fluid Dynamics Conference, American Institute of Aeronautics and Astronautics, Reston (1996) |
| [14] | Dietz, A. J. Boundary-layer receptivity to transient convected disturbances. AIAA Journal, 36, 1171-1177(1998) |
| [15] | Dietz, A. J. Local boundary-layer receptivity to a convected free-stream disturbance. Journal of Fluid Mechanics, 378, 291-317(1999) |
| [16] | Wu, X. S. On local boundary-layer receptivity to vortical disturbances in the free stream. Journal of Fluid Mechanics, 449, 373-393(2001) |
| [17] | Wu, X. S. Receptivity of boundary layers with distributed roughness to vortical and acoustic disturbances:a second-order asymptotic theory and comparison with experiments. Journal of Fluid Mechanics, 431, 91-133(2001) |
| [18] | Zhang, Y. M. and Zhou, H. Numerical study of local boundary layer receptivity to freestream vortical disturbances. Applied Mathematics and Mechanics (English Edition), 26(5), 547-554(2005) DOI 10.1007/BF02466327 |
| [19] | Shen, L. Y. and Lu, C. G. Boundary-layer receptivity under the interaction of free-stream turbulence and localized wall roughness. Applied Mathematics and Mechanics (English Edition), 37(3), 349-360(2016) DOI 10.1007/s10483-016-2037-6 |
| [20] | Ricco, P. The pre-transitional Klebanoff modes and other boundary-layer disturbances induced by small-wavelength free-stream vorticity. Journal of Fluid Mechanics, 638, 267-303(2009) |
| [21] | Zuccher, S. and Luchini, P. Boundary-layer receptivity to external disturbances using multiple scales. Meccanica, 49, 441-467(2014) |
| [22] | Shen, L. Y., Lu, C. G., Wu, W. G., and Xue, S. F. A high-order numerical method to study threedimensional hydrodynamics in a natural river. Advances in Applied Mathematics and Mechanics, 7, 180-195(2015) |
| [23] | Lu, C. G., Cao, W. D., Zhang, Y., and Peng, J. Large eddies induced by local impulse at wall of boundary layer with pressure gradients. Progress in Natural Science, 18, 873-878(2008) |
| [24] | Zhang, Y. M., Zaki, T., Sherwin, S., and Wu, X. S. Nonlinear response of a laminar boundary layer to isotropic and spanwise localized free-stream turbulence. The 6th AIAA Theoretical Fluid Mechanics Conference, American Institute of Aeronautics and Astronautics, Reston (2011) |
| [25] | Bodonyi, R. J. Nonlinear triple-deck studies in boundary-layer receptivity. Applied Mechanics Reviews, 43, S158-S166(1990) |
| [26] | Zhou, M. D., Liu, D. P., and Blackwelder, R. F. An experimental study of receptivity of acoustic waves in laminar boundary layers. Experiments in Fluids, 17, 1-9(1994) |
| [27] | Lu, C. G. and Shen, L. Y. Numerical study on boundary-layer receptivity with localized wall blowing/suction (in Chinese). Acta Physica Sinica, 64, 224702(2015) |
 2016, Vol. 37
2016, Vol. 37












