Shanghai University
Article Information
- Chao ZHANG, Zhenhua WAN, Dejun SUN. 2016.
- Mode transition and oscillation suppression in supersonic cavity flow
- Appl. Math. Mech. -Engl. Ed., 37(7): 941-956
- http://dx.doi.org/10.1007/s10483-016-2095-9
Article History
- Received 2015-11-10;
- in final form 2016-03-02
Cavity flows have received great attention in the past decades in both experimental and numerical investigations due to its relevance to many practical engineering applications. The research of supersonic cavity flow was motivated by the development of the weapon bay for stealth aircraft in the 1980s[1]. Large oscillation amplitude exceeding 160 dB may occur even in subsonic cavity flows, resulting in structural fatigue. Cavity geometry was characterized by the length-to-depth ratio (L/D) which determines the flow fields to be closed, open, or transitional[2]. Closed cavity flow fields are typically associated with shallow cavities (L/D > 13). In this type of flow, the shear layer hits the cavity floor, forming two recirculating regions inside the cavity. Open cavity flow fields are typically associated with deep cavities (L/D < 10). The flow of this type consists of internal and external regions separated by the shear layer along the cavity opening, wherein the internal region contains a large recirculating flow. An intermediate value of 10 < L/D < 13 is associated with transitional cavity flow fields.
Generally, the cavity flow oscillations are regarded as flow-acoustic resonance phenomenon. Its first detailed description was credited to Rossiter[3], who proposed a semi-empirical formula to predict the resonant frequencies based on the feedback mechanism. Heller and Bliss[4] modified Rossiter's semi-empirical formula. As Rowley and Williams[5] mentioned, the feedback mechanism contains only four elemental fluid dynamic processes: (i) shear layer amplification of vortical disturbances; (ii) pressure wave generation through vortex-surface interaction; (iii) upstream propagation of acoustic waves; (iv) receptivity at the front wall of the cavity and converting pressure waves into vorticity waves.
The cavity flow modes can be affected by the cavity geometry and the inflow conditions, wherein the thickness of the incoming boundary layer was recognized as a decisive factor for the mode selection[6]. In subsonic or incompressible cavity flow with fixed inflow velocity, many researchers[7, 8, 9, 10] have studied the flow modes by changing the cavity length (L). Only Rowley et al.[8] considered the effect of the boundary layer momentum thickness ( θ ) with fixed cavity geometry. Overall, the cavity flow modes are affected by the ratio of the cavity length over the momentum thickness of the separating boundary layer (L/ θ ). As it increases, a transition from the steady mode to the shear layer mode then to the wake mode has been observed. However, there is no clear answer to whether the same mode transition can be found in the supersonic cavity flow.
How the coherent structures changed was not intuitive for the mode transition mentioned in the previous literature. To obtain information about the coherent structures, the dynamic mode decomposition (DMD) approach[11, 12, 13] based on the Koopman analysis of dynamical system is an effective method, which attempts to represent a data sequence by orthogonalizing it in time. A typical work about application of the DMD to open cavity flow can be seen in Seena and Sung[14], who used the DMD to analyze the self-sustained oscillations for incompressible turbulent cavity flows. However, the report about the DMD used for compressible cavity flows has not been observed, although there is no technical difficulty. In our research work, the DMD is utilized to get the dynamic modes for supersonic cavity flows to display the mode transition. Meanwhile, the global oscillation frequencies showing by the energy spectrum can be compared with the local power spectral density (PSD) results. Extensive studies have been carried out to control oscillations of cavity flow[5, 15, 16]. For passive control, the common method is to mount spoilers at the upstream of the cavity front wall or replace the cavity front/rear wall by ramps[17, 18, 19]. The other method such as using a sub-cavity on the front wall of the cavity covered by a flat plate[20, 21] has been proven to be effective. For active open-loop control, the mass injection is frequently utilized at the cavity leading edge or the upstream of it[22, 23, 24]. The existing results show that passive control and active open-loop control can be achieved for supersonic cavity flows, while active closed-loop control has not been used until now. However, research works about cavity flow control always focus on the suppression of the oscillation amplitude. To the best of the authors' knowledge, the mode transition under control has rarely been discussed.
In this paper, the effect of the incoming boundary layer thickness on the two-dimensional supersonic cavity flow is investigated. As the boundary layer thickness decreases, the dominant mode transition from the steady mode to the Rossiter Ⅱ mode then to the Rossiter Ⅲ mode occurs due to the change of vortex-corner interactions. Meanwhile, the low frequency mode appears. Different from the subsonic cavity flow, we do not obtain the wake mode in the current simulation even if the momentum thickness is very small. Then, we investigate a passive control technique by substituting the cavity trailing edge with a quarter-circle. Suppression of pressure oscillations can be achieved, and the dominant mode transition from the Rossiter Ⅱ mode to the Rossiter Ⅲ mode also occurs as the effective cavity length increases. Furthermore, we consider an active control technique using the steady subsonic mass injection at the upstream of leading edge. The shear layer is lifted up and thickened. Consequently, the vortex-corner interaction is greatly weakened or completely avoided. Thus, the flow may develop into steady mode.
2 Numericalmethods 2.1 Physics modelThe schematic description of the two-dimensional open cavity model with/without control is shown in Fig. 1. First, the baseline cavity (named as R0) has a depth (D) of 5 cm, and its length (L) is given as 4D. The origin of the coordinate is located at the cavity leading edge. The Mach number of the incoming flow is 1.8. At the separation point, the momentum thickness θ of the incoming flow is obtained from the time-averaged field. Based on the cavity depth (D) and the freestream velocity (u∞), the Reynolds number ReD = ρu∞D/μ is 4 500. Then, a passive control technique by substituting the cavity trailing edge with a quarter-circle is studied, with the radius (R) equal to D/5, 3D/5, and D, respectively. The corresponding cavities are named as R1, R3, and R5 for simplicity. Also, we consider an active control technique using the steady subsonic mass injection at the upstream of leading edge. The jet has a streamwise length of 0.08D and is positioned at a distance of 0.08D from the leading edge cavity lip. A monitor is located in the shear layer near the cavity trailing edge (x/D = 3.9, y/D = 0). During the whole computation, the time-dependent flow information, such as the local wall static pressure, is recorded at the monitor, and the frequency spectrum of the pressure oscillations can be obtained through the PSD technique.

|
| Fig. 1 Schematic of cavity model with/without passive and active control |
The governing equations are the compressible Navier-Stokes equations, i.e.,
where The molecular viscosity coefficient μ is obtained from the Sutherland law, and the Prandtl number is a constant (Pr = 0.7). The ratio of specific heats is γ = 1.4, and R is the gas constant. We use the OpenFOAM C++ library to solve the governing equations. A densitybased compressible flow solver, which is based on the central upwind schemes of Kurganov and Tadmor[25], is used for spatial discretization. The time integration is performed by a secondorder implicit backward approach, and a small time-step of 4.0×10-8 s is used.A laminar supersonic flow (Ma = 1.8), which has a boundary layer thickness δ, is applied to the inlet boundary. The incoming velocity profile is given by the approximate solutions of two-dimensional finite length plate boundary layer. The static pressure p is 100 kPa, and the static temperature T is 300 K. On the solid walls of the cavity, no-slip and adiabatic conditions are applied, given as
For the upper and outflow boundaries, the non-reflecting boundary condition (wave transmissive outflow condition) of pressure is utilized, combined with where n is the direction normal to the surface. The upper cavity region is initialized with the Mach 1.8 inflow, while the fluid in the inside cavity region contains the quiescent state at the initial time. 2.3 ValidationThe simulation of the two-dimensional supersonic (Ma = 1.83) cavity flow with L/D = 1 is chosen to validate the present numerical method. The oscillation frequency (the Strouhal number) is compared with the other results[20, 26, 27], as shown in Table 1. The theoretical result of Nishioka et al.[27] considered the effect of the cavity geometry. The comparison shows that the present numerical method is acceptable with the tolerable accuracy.
A non-uniform structured grid is used with the mesh points clustered near walls of the baseline cavity. The domain is composed of inside cavity and upper cavity regions. The length from the inlet to the cavity leading edge is equal to 6.82D, and 12D is extended from the cavity trailing edge to the outlet. The upper cavity region is built up by 656×150 rectangular cells, while 200×152 rectangular cells are used inside the cavity region. The minimum cell length equals 1.0×10-4 m. A finer mesh, which is built up by 1 000×300 and 300×200 rectangular cells, is created to validate the grid resolution. For the cavity flow with passive control, a similar structured grid system is built up, while C-shaped cells are used around the quarter-circle.
The distributions of time-averaged streamwise velocity component at five streamwise locations for the uncontrolled cavity flow with L/ θ ≈ 83.2 are shown in Fig. 2, which shows that nearly the same distributions are obtained using the two different meshes, and the grid independence is obtained.

|
| Fig. 2 Time-averaged streamwise velocity component distributions at five streamwise locations for uncontrolled cavity flow with L/θ ≈ 83.2 under two different meshes |
As aforementioned, the flow-acoustic resonant mechanism of cavity oscillations was first proposed by Rossiter[3]. With the assumption that the sound speed inside the cavity is equal to that in a free stream, the semi-empirical formula is shown as
Heller and Bliss[4] modified Rossiter's formula by assuming that the sound speed inside the cavity is equal to that in the stagnation free stream. The semi-empirical formula is then rewritten as where Stn is the Strouhal number, fn is the frequency at a given mode number n, u∞ is free stream velocity, L is the cavity length, Ma is the free stream Mach number, and κ = 0.57 and α = 0.25 are the empirical constants corresponding to the average convection speed of disturbances in the shear layer and a phase delay given by Rossiter[3]. The sound pressure level (pSPL) is obtained from ρPSD[28] , which is defined by where pref = 2× 10-5 Pa is the reference pressure. 3.1 Effect of incoming boundary layer thickness Many flow and geometric parameters can affect the choice of cavity oscillation modes, such as the incoming boundary layer thickness, the freestream Mach number, and the length-todepth ratio. For the subsonic cavity flow, there exists a minimum cavity length below which no oscillation occur for given flow conditions[8, 10, 29]. Also, the flow is steady below a minimum velocity for a given cavity geometry and boundary layer thickness at the separation point[8]. Now, the freestream Mach number is 1.8, and the length-to-depth ratio is fixed at 4. The effects of the incoming boundary layer thickness are investigated. Figure 3 shows the PSD peak frequencies at the monitor for baseline cavities with different L/ θ . The flow mode with the highest PSD peak is the dominant mode, and the Strouhal number for this mode is represented by solid circles. When L/ θ is lower than about 53, the shear layer cannot roll up, and the cavity has no oscillation (St = 0), indicating that there is a maximum momentum thickness of the incoming flow for the onset of oscillations. As L/ θ increases, the Strouhal number of the dominant oscillation mode becomes lager, and the cavity flow turns into the shear layer mode (the Rossiter Ⅱ mode). Note that, the Rossiter Ⅲ mode and the low-frequency mode are observed as L/ θ larger than about 66. The dominant mode transition from the Rossiter Ⅱ mode to the Rossiter Ⅲ mode occurs at L/ θ ≈ 90. The Rossiter Ⅱ mode and the low-frequency mode are also observed. Overall, the mode transition we obtained is quite similar to the subsonic cavity flow. However, no wake mode is found even if the momentum thickness is very small. In the subsonic cavity flow, Colonius et al.[7] found that the laminar boundary layer separation upstream of the cavity was the cause of the transition to wake mode and gave a criterion based on the adverse pressure gradient at the separation point = 0.09. When −λ > 0.09, the wake mode appeared. In our simulation, −λ is always lower than 0.09. Hence, the wake mode is not observed.
= 0.09. When −λ > 0.09, the wake mode appeared. In our simulation, −λ is always lower than 0.09. Hence, the wake mode is not observed.

|
| Fig. 3 Strouhal numbers St for baseline cavities with different L/θ (NO=no oscillation; SLⅡ=Rossiter Ⅱ mode is dominant mode; SL Ⅲ=Rossiter Ⅲ mode is dominant mode) |
We choose three typical cases shown in Table 2 (B2-B4) to carry on the DMD analysis in order to show dynamic mode structures of different shear layer modes and compare the global oscillation frequencies with the PSD results. Figure 4 shows the energy spectrum, and Fig. 5 shows the dynamic mode structure visualized by the vorticity. The DMD modes with the highest energy are marked 0 in the spectra, corresponding to the time-averaged modes. Flow structures for these modes are quite similar. The dominant oscillation modes are DMD modes with the second highest energy marked 1 in the spectra, and the oscillation frequencies are quite consistent with the PSD results. The same conclusions can be obtained for other oscillation modes. It should be pointed out that there are other modes with the oscillation frequency quite close to the marked ones for the B4 case possibly because of the jittering effect. In Figs. 5(a), 5(b), and 5(e), two vortices can be observed in the shear layer, indicating the Rossiter Ⅱ mode.There are three vortices in the shear layer for Figs. 5(c) and 5(d), which represent the Rossiter Ⅲ mode. Hence, the dominant mode transition can be clearly observed through comparing Fig. 5(b) with Fig. 5(d).
 |

|
| Fig. 4 Energy spectrum given by DMD for baseline cavities with three different L/ θ shown in Table 2 |

|
| Fig. 5 DMD modes (real part only) visualized by vorticity for baseline cavities with three different L/ θ shown in Table 2 |
In order to explain the generation of the low-frequency mode, we discuss the interaction of the shear layer vortex with the downstream cavity edge. Rockwell and Knisely[30, 31] classified the vortex-corner interaction as complete clipping (CC), partial clipping (PC), partial escape (PE), and complete escape (CE), and related the generation of the low frequency components in low speed flow with the alternating occurrence of these vortex-corner interactions. From the instantaneous fields for the baseline cavity with L/ θ ≈ 58.8, one can only find a single and stable PE vortex-corner interaction, resulting in single and stable Rossiter Ⅱ modes. For the other two cases, one can find a PC vortex-corner interaction and a PE vortex-corner interaction similar to the below R0 case or more vortex-corner interactions. The alternating occurrence of these vortex-corner interactions produces the low-frequency mode.
The boundary layer thickness not only affects the oscillation mode but also affects the oscillation amplitude. Figure 6 shows the overall sound pressure level (OASPL) distributions on the floor for the above three baseline cavities. We can get that the OASPL increases as the momentum thickness of the incoming flow decreases. Note that, the OASPL distribution for the cavity with L/ θ ≈ 90.5 is different from the other two because of the dominant mode transition from the Rosster Ⅱ to the Rossiter Ⅲ. The pressure oscillations are related to the features of the shear layer which can be described using the velocity fluctuations[32]. Figure 7 shows the velocity fluctuations for the above three baseline cavities at three streamwise locations. The amplitudes for both the horizontal velocity fluctuations and the vertical velocity fluctuations increase as the momentum thickness of the incoming flow decreases, indicating that the growth rate of the shear layer increases. The enhancement of the shear layer instability should be responsible for the increasing pressure oscillations.

|
| Fig. 6 OASPL distributions on floor for baseline cavities with three different L/ θshown in Table 2 |

|
| Fig. 7 Velocity fluctuations at three streamwise locations for baseline cavities with three different L/ θ shown in Table 2 (horizontal velocity fluctuations (a), (b), and (c); vertical velocity fluctuations (d), (e), and (f)) |
Previous studies have shown that flow oscillations in the cavity can cause structural fatigue, and the cavity trailing edge plays an important role in the feedback process of the oscillation. As the shear layer hits the cavity trailing edge, a part of the fluid continues to move downstream of the cavity, and the other goes into the cavity. It is natural to consider that we can break or weaken such a feedback process by just modifying the shape of this trailing edge. In this paper, we investigate a passive control method of substituting the cavity trailing edge with a quartercircle, and the radius of the circle equals D/5, 3D/5, and D, respectively. The corresponding cavities are named cavity R1, R3, and R5 for simplicity. The parameters can be seen in Table 3, and the effective cavity length equals 4D + (1 − 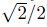 )R.
)R.
Figure 8 shows the SPLs of the monitor with/without passive control. Through a comparison between Figs. 8(a) and 8(b), it can be observed that the jittering effect is removed by substituting the cavity trailing edge with a quarter-circle whose radius equals D/5. However, the cavity oscillation mode is unchanged (the SL Ⅱ mode), the dominant oscillation frequency and amplitude are rarely affected. As the radius of the circle for passive control increases, the amplitude shifts to lower levels. One can see that the SPL corresponding to the dominant oscillation frequency in the cavity is reduced by about 3 dB and 11 dB when the radius of the quarter-circle equals 3D/5 and D, respectively. It is proved to be effective to reduce the oscillations by current control technique. The cavity oscillation mode changes from the SL Ⅱ mode to the SL Ⅲ mode. Note that, the oscillation mode of the controlled cavity R5 is single and the stable Rossiter Ⅲ mode. As shown in Table 3, the dominant mode transition is conformed to the trend, as illustrated in Fig. 3.

|
| Fig. 8 SPLs at monitor for cavities with/without passive control shown in Table 3 |
 R
R
 |
The enstrophy distribution can describe the magnitude of the vorticity and the interaction of the shear layer with the recirculation zone in supersonic cavity flows. Instantaneous enstrophy fields for the uncontrolled cavity are shown in Fig. 9. Figures 9(a)-9(c) show the PC vortex-corner interaction, while Figs. 9(d)-9(f) show the PE vortex-corner interaction. The alternating occurrence of these vortex-corner interactions produces the low-frequency mode. For the controlled cavity R5, the instantaneous enstrophy fields are shown in Fig. 10. The present vortex-corner interaction is a single and stable PE type, which results in a shear layer mode (the Rossiter Ⅲ mode) without any other component. The flow mode can be influenced by not only L/ θ but also cavity geometry.

|
| Fig. 9 Instantaneous enstrophy fields for uncontrolled cavity R0, where (a)-(c) show PC vortexcorner interaction and (d)-(f) show PE vortex-corner interaction |

|
| Fig. 10 Instantaneous enstrophy fields for controlled cavity R5, showing single and stable PE vortexcorner interactions |
The OASPL distributions on the floor for cavities with/without passive control are shown in Fig. 11. One can see that the pressure oscillations are suppressed as the radius of the quartercircle increases, the OASPL can even be reduced by approximate 23 dB near x/D = 1.5 on the cavity floor for the R5 cavity. Figure 12 shows the velocity fluctuations for cavities with/without passive control. The amplitudes for both the horizontal velocity fluctuations and the vertical velocity fluctuations decrease as the radius of the quarter-circle increases, indicating that the growth rate of the shear layer decreases. In other words, the shear layer instability is weakened.Also, comparing Fig. 9 with Fig. 10, the enstrophy around the recirculation zone is rather smaller under control, indicating that the interaction of the shear layer with the recirculation zone is weakened. These are possibly the reasons for the suppression of the pressure oscillations.

|
| Fig. 11 OASPL distributions on floor for cavities with/without passive control shown in Table 3 |

|
| Fig. 12 Velocity fluctuations at three streamwise locations for cavities with/without passive control shown in Table 3 (horizontal velocity fluctuations (a), (b), and (c); vertical velocity fluctuations (d), (e), and (f)) |
Active control for the cavity pressure oscillations often requires large actuator power to be effective, and mass injection at the upstream of the cavity leading edge is a common choice. Now, we consider a subsonic mass injection by specifying a jet ejecting vertically. Its velocity profile is defined as
where A represents the maximum Mach number of the jet flow, a∞ is the sound speed of the free-stream flow, and x1 and x2 are the x -coordinates of the jet edges. A mass injection with the parameter of A = 0.29 is applied to the B2 case. The flow conditions of the supersonic cavity flow with/without upstream mass injection are listed in Table 4. |
The pressure history at the monitor for the cavities with/without upstream mass injection can be seen in Fig. 13. For the uncontrolled case, the periodical flow is obtained. As aforementioned, the cavity flow is dominated by a shear-layer mode. For the controlled cavity, pressure oscillations are diminishing, and the steady state is achieved finally. L/ θ under control is about 49.1, which is less than the minimum value for the onset of oscillations (L/ θ ≈ 53). From the flow field, we find that the shear layer is thickened and lifted up, which greatly weakens or completely avoids the vortex-corner interaction around the trailing edge.

|
| Fig. 13 Pressure history at monitor for cavities with/without upstream mass injections shown in Table 4 |
The characteristics of oscillations in the two-dimensional supersonic cavity flows with/ without control are investigated by the DNS based on the OpenFOAM C++ Library.
For the baseline cavity with a length-depth ratio (L/D) fixed at 4 in a freestream of Mach number 1.8, we study the effects of the incoming boundary layer thickness. There is a maximum momentum thickness of the incoming flow for the onset of oscillations at low Reynolds number laminar flows. Below this critical value, the cavity flow loses stability to the shear layer mode (the Rossiter mode). As the decline of the boundary layer thickness, the amplitudes of the pressure oscillations (OASPL) increase, and the dominant mode transition from the Rossiter Ⅱ to the Rossiter Ⅲ is clearly shown by the dynamic modes obtained from the DMD. The decrease of the boundary layer thickness further destabilizes the shear layer showing by the velocity fluctuations. Vortices in the shear layer become more unstable and thus results in different vortex-corner interactions, which are responsible for such a mode transition. Note that, we do not obtain the wake mode in current simulation even if the momentum thickness is very small. Furthermore, a passive control technique by substituting the cavity trailing edge with a quarter-circle is studied with the radius (R) of the circle equals D/5, 3D/5, and D, respectively. The results indicate that the amplitudes of the pressure oscillations are reduced as the increase of the radius of the circle. Compared with R0, the OASPL at the cavity floor can even be reduced by up to 23 dB in R5. Hence, the current passive control method is proven to be quite effective. As the effective cavity length increases, the dominant mode transition from the Rossiter Ⅱ to the Rossiter Ⅲ mode occurs, which conforms to the trend for uncontrolled cavity with increasing L/ θ . Without control, there are different kinds of vortex-corner interactions near the downstream edge, resulting in multiple oscillation modes. Under passive control with R = D, the vortex-corner interaction becomes stable and single, and the interaction of the shear layer with the recirculation zone is weakened. Therefore, the flow only presents the Rossiter Ⅲ mode, and the amplitude of the pressure oscillation is suppressed. Active control using steady subsonic mass injection upstream of the cavity leading edge can stabilize the flow through thickening the shear layer and lifting up it, which can greatly weaken or completely avoid the vortex-corner interaction. Overall, the parameter L/ θ plays an important role in determining the flow mode for controlled cavity.
Acknowledgements The authors especially thank the OpenFOAM Foundation for the free open source CFD software package—OpenFOAM.
| [1] | Cattafesta, L., Shukla, D., Garg, S., and Ross, J. Development of an adaptive weapons-bay suppression system. The 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, American Institute of Aeronautics and Astronautics, Reston, 676-682(1999) |
| [2] | Stallings, R. L. and Wileox, F. J. Experimental cavity pressure distributions at supersonic speeds. NASA Technical Paper 2683, NASA Langley Research Center, Virginia (1987) |
| [3] | Rossiter, J. E. Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds. No. 64037, Royal Aircraft Establishment Technical Report, Farnborough (1964) |
| [4] | Heller, H. H. and Bliss, D. B. The physical mechanism of flow induced pressure fluctuations in cavities and concepts for their suppression. AIAA 2nd Aero-Acoustics Conference, American Institute of Aeronautics and Astronautics, Reston (1975) |
| [5] | Rowley, C. W. and Williams, D. R. Dynamics and control of high-Reynolds-number flow over open cavities. Annual Review of Fluid Mechanics, 38, 251-276(2006) |
| [6] | Tam, C. K. W. and Block, P. J. W. On the tones and pressure oscillations induced by flow over rectangular cavities. Journal of Fluid Mechanics, 89(2), 373-399(1978) |
| [7] | Colonius, T., Basu, A. J., and Rowley, C. W. Numerical investigation of the flow past a cavity. The 5th AIAA/CEAS Aeroacoustics Conference, American Institute of Aeronautics and Astronautics, Reston (1999) |
| [8] | Rowley, C. W., Colonius, T., and Basu, A. J. On self-sustained oscillations in two-dimensional compressible flow over rectangular cavities. Journal of Fluid Mechanics, 455, 315-346(2002) |
| [9] | Rubio, G., de Roeck, W., Baelmans, M., and Desmet, W. Numerical identification of flow-induced oscillation modes in rectangular cavities using large eddy simulation. International Journal for Numerical Methods in Fluids, 53, 851-866(2007) |
| [10] | Gharib, M. and Roshko, A. The effect of flow oscillations on cavity drag. Journal of Fluid Mechanics, 177, 501-530(1987) |
| [11] | Schmid, P. J. Dynamic mode decomposition of numerical and experimental data. Journal of Fluid Mechanics, 656, 5-28(2010) |
| [12] | Schmid, P. J., Li, L., Juniper, M. P., and Pust, O. Applications of the dynamic mode decomposition. Theoretical and Computational Fluid Dynamics, 25, 249-259(2011) |
| [13] | Wan, Z., Yang, H., Zhou, L., and Sun, D. Mode decomposition of a noise suppressed mixing layer. Theoretical and Applied Mechanics Letters, 3(4), 042007(2013) |
| [14] | Seena, A. and Sung, H. J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations. International Journal of Heat and Fluid Flow, 32, 1098-1110(2011) |
| [15] | Williams, D. R. and Rowley, C. W. Recent progress in closed-loop control of cavity tones. The 44th AIAA Aerospace Sciences Meeting and Exhibit, American Institute of Aeronautics and Astronautics, Reston (2006) |
| [16] | Cattafesta, L. N., Song, Q., Williams, D. R., Rowley, C. W., and Alvi, F. S. Active control of flow-induced cavity oscillations. Progress in Aerospace Sciences, 44, 479-502(2008) |
| [17] | Dudley, J. G. and Ukeiley, L. Detached eddy simulation of a supersonic cavity flow with and without passive flow control. The 20th AIAA Computational Fluid Dynamics Conference, American Institute of Aeronautics and Astronautics, Reston (2011) |
| [18] | Vikramaditya, N. S. and Kurian, J. Pressure oscillations from cavities with ramp. AIAA Journal, 47, 2974-2984(2009) |
| [19] | Vikramaditya, N. S. and Kurian, J. Experimental study of influence of trailing wall geometry on cavity oscillations in supersonic flow. Experimental Thermal and Fluid Science, 54, 102-109(2014) |
| [20] | Alam, M., Matsuo, S., Teramoto, K., Setoguchi, T., and Kim, H. D. A new method of controlling cavity-induced pressure oscillations using sub-cavity. Journal of Mechanical Science and Technology, 21, 1398-1407(2007) |
| [21] | Lee, Y. K., Kang, M. S., Kim, H. D., and Setoguchi, T. Passive control techniques to alleviate supersonic cavity flow oscillation. Journal of Propulsion and Power, 24, 697-703(2008) |
| [22] | Zhuang, N., Alvi, F. S., and Shih, C. Another look at supersonic cavity flows and their control. The 11th AIAA/CEAS Aeroacoustics Conference (26th AIAA Aeroacoustics Conference), American Institute of Aeronautics and Astronautics, Reston (2005) |
| [23] | Lusk, T., Cattafesta, L., and Ukeiley, L. Leading edge slot blowing on an open cavity in supersonic flow. Experiments in Fluids, 53, 187-199(2012) |
| [24] | Li, W., Nonomura, T., and Fujii, K. Mechanism of controlling supersonic cavity oscillations using upstream mass injection. Physics of Fluids, 25, 086101(2013) |
| [25] | Kurganov, A. and Tadmor, E. New High-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. Journal of Computational Physics, 160, 241-282(2000) |
| [26] | Zhang, X. and Edwards, J. A. An investigation of supersonic oscillatory cavity flows driven by thick shear layers. Aeronautical Journal, 94, 355-364(1990) |
| [27] | Nishioka, M., Asai, T., Sakaue, S., and Shirai, K. Some thoughts on the mechanism of supersonic cavity flow oscillation, part 2, a new formula for the oscillation frequency. Journal of Japan Society of Fluid Mechanics, 21, 368-378(2002) |
| [28] | Peng, S. H. Simulation of turbulent flow past a rectangular open cavity using DES and unsteady RANS. The 24th Applied Aerodynamics Conference, American Institute of Aeronautics and Astronautics, Reston (2006) |
| [29] | Sarohia, V. Experimental investigation of oscillations in flows over shallow cavities. AIAA Journal, 15, 984-991(1977) |
| [30] | Rockwell, D. and Knisely, C. Vortex-edge interaction:mechanisms for generating low frequency components. Physics of Fluids, 23(2), 239-240(1980) |
| [31] | Knisely, C. and Rockwell, D. Self-sustained low-frequency components in an impinging shear layer. Journal of Fluid Mechanics, 116, 157-186(1982) |
| [32] | Gloerfelt, X., Bailly, C., and Juvé, D. Direct computation of the noise radiated by a subsonic cavity flow and application of integral methods. Journal of Sound and Vibration, 266, 119-146(2003) |
 2016, Vol. 37
2016, Vol. 37














