Shanghai University
Article Information
- Wei KONG, Jisheng LUO
- Global instability of Stokes layer for whole wave numbers
- Applied Mathematics and Mechanics (English Edition), 2016, 37(8): 999-1012.
- http://dx.doi.org/10.1007/s10483-016-2113-8
Article History
- Received May. 18, 2015
- Revised Mar. 23, 2016
It has been known that the Stokes layer is one of the common unsteady flows which is induced in the condition of an infinite oscillating flat plate or oscillating pressure gradient. This flow can be usually observed in the undersea and the coast. Generally,it can be divided into two kinds. The one which is generated in an infinite flat plate oscillating in its own plane is called the semi-infinite Stokes layer,and the other which is driven by the periodic pressure gradient in channels or pipes is called the finite Stokes layer.
For many years,the Stokes layer is a classical model for understanding the instability of the unsteady flows. Generally,there are two approaches for investigating the instability of the Stokes layers. The first one is the global instability based on the Floquet theory which is used to derive those equations with multi-variables. The other is called the instantaneous instability,i.e.,the local instability. In this approach,the base flow is quasi-stationary for its insignificant variation in the temporal scale. For the given ‘freezing’ time,the local instability can be obtained by solving the Orr-Sommerfeld (O-S) equations. Then,the instability of the whole periodic flow can be obtained by integrating the local eigenvalue in the temporal direction. In most investigations,the Reynolds number is defined as Reδ = U0δ/ν,where U0 is the velocity amplitude of the oscillating plate(s) or the external flow,
In the early stages,the instability of the Stokes layer is analyzed by the energy method,but the critical Reynolds number obtained is quite small. Collins[1] considered the quasi-steady assumption by using a quite stable instantaneous ‘frozen’ profile,however,the critical Reynolds number is only 21.4. Later,the transient stability was considered by Davis and von Kerczek[2],however,the critical Reynolds number acquired is still low as O(10). Cowley[3] investigated the instability of the Stokes layer by using a multiple-scales method in the time. He found that the critical Reynolds number at the end of acceleration is larger than that at the beginning of acceleration. On the other hand,based on the Floquent theory,von Kerczek and Davis[4] and Hall[5] investigated the linear instability of the finite and semi-infinite Stokes layers,respectively. Their results indicate that no unstable disturbance can be found while the Reynolds number is up to 800 for the finite Stokes layer (h = 8) and 320 for the semi-infinite Stokes layer. Akhavan et al.[6] concerned the linear and nonlinear instabilities of the Stokes layer in a channel by using the direct numerical simulation (DNS). It was shown that the disturbances were all stable even as Reδ was up to 1000. In summary,the outcomes at that time suggest that the Stokes layers may be linearly stable for all Reynolds numbers.
In the recent years,the linear instability problem was reconcerned by many investigators,and the results were very interesting. In 2002,the linear instability of a flat Stokes layer was restudied with the Floquet theory by Blennerhassett and Bassom[7]. They gave the neutral curve of global instability in the range 0.2 ≤ α ≤ 0.5 and claimed that the critical Reynolds number was about 1 416,where α was the wave number. Later,Hall[8] concerned the inviscid instability of the Stokes layer by invoking the Floquet thoery and discussed the relationship between the Floquet mode and the instantaneous mode. Blennerhassett and Bassom[9] investigated the linear instability of the finite Stokes layers and found that the neutral curve of global instability would be close to the infinite one if the distance of the channel was large enough (h ≥ 14). Luo and Wu[10] investigated this problem by using the numerical methodology based on the instantaneous instability theory. They suggested that the global instability could be well predicted by the local instability theory,and the result obtained was found to be in excellent accord with the result of Ref. [7]. Thomas et al.[11] investigated the time evolutions of the disturbances by the numerical simulation of the velocity-vorticity formulation of the governing equations. The neutral curve obtained successfully matched the results of previous studies. Later,the three-dimensional linear instability of the Stokes layer in a long oscillating cylinder was also studied by means of the Floquet theory[12]. It was shown that the effect of three-dimensionality would be insignificant except that the radius was small enough. Recently,Thomas et al.[13] studied the evolutions of disturbances by introducing a spatially localised impulsive forcing. It was found that the spatial-temporal evolution of the flow displayed a family-tree-like structure. In 2015,they considered the linear instability problem of a Stokes layer[14],which superimposed large-frequency components,by using both the DNS and Floquet analyses. The results indicated that only 1% perturbation would be able to result in a reduction of the critical Reynolds number of nearly 60%,which was in excellent coincidence with the experiments[15-18].
Despite the fact that the linear instabilities of Stokes layers were studied by many investigators,the neutral curves obtained in previous works were presented for a rather limited range of wave numbers,α ∈ (0.2,0.5),i.e.,the neutral curves are incomplete. There are several questions which are not discussed in previous studies. What are the characteristics of the neutral curves for α > 0.5 and α < 0.2? Will the global instability be found at all wave numbers? What are the instability characteristics for different ranges of wave numbers?
The aim of this paper is to answer the above questions. The global instability of the semiinfinite Stokes layer is analyzed by the numerical methodology in detail. The characteristics of the evolutions of disturbances are described by means of the instantaneous instability theory.The neutral point is redefined in this paper,and the neutral curve of global instability including the added portion is presented with this new definition.
2 Formulation of linear perturbation equationIn this paper,an infinite Stokes layer generated by a synchronously oscillating flat plate is concerned. The oscillating velocity of the flat plate is U0 cos(Ωt*),where U0 is the maximum velocity of the oscillating flat plate,Ω and t* are the oscillating frequency and time,respectively. The thickness of the Stokes layer is defined as 

The equations are normalized by the boundary layer and the oscillating parameters. The coordinates (x*,y*) are scaled on δ,velocity components (u,v) on U0,the pressure P * on ρU0 2,where x* is the oscillation direction of the flow,y* is the normal direction,and ρ is the density. The time t* is normalized by 1/Ω.
Then,the base flow can be written as
The perturbance can be written as
where c.c. represents the complex conjugates,and α is the streamwise wave number. Insert Eq. (2) into the incompressible Navier-Stokes equations. When Є 
The boundary conditions are
In the Floquet theory,the disturbances can be written as
where u1,v1,and p1 are the time-periodic functions. σ is the Floquet exponent,which represents the net growth rate of a disturbance. A0 is the initial amplitude of a disturbance.
In order to study the instantaneous instability of the Stokes layer,a multiple-scale method is used by introducing an additional time parameter τ,which is normalized by δ/U0. Therefore,the time t is treated as a slow variable with τ,i.e.,τ = Re t. Then,the disturbances are written as
where ω(t) is the complex frequency of the disturbance. Inserting Eq. (6) into Eq. (3),the O-S equation is followed as
Equation (7) together with the boundary conditions
forms the eigenvalue problem to determine the instantaneous eigenvalue ω(t) = ωr(t) + iωi(t),where the imaginary part ωi(t) is the instantaneous growth rate of the disturbance.
At present,the numerical methodology is adopted to study the linear evolutions of the disturbances,which satisfies Eq. (3). The difference scheme suggested by Malik[19] is used in the y- direction. A 3rd-order difference scheme is adopted in the time in this form of
with the time step π × 10-5. The initial condition of Eq. (3) is followed as
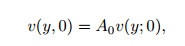 (10)
(10) where v(y; 0) is the initial eigenfunction obtained by Eq. (7),and the initial amplitude A0 = 10-9.
3 Results and discussion 3.1 Evolution of disturbances at 0.2 < α < 0.5It has been known that the previous studies focus on the global linear instability for 0.2 < α < 0.5,therefore,the present calculations are firstly conducted for the cases of α = 0.3 and α = 0.5. Figure 1 displays the evolutions of the disturbance amplitude |u| measured by the maximum streamwise velocity along the normal direction,i.e.,max|u|. It can be found that max|u| indicates the characteristic of a Floquet global mode,which has a peak value in one oscillation cycle. For a given wave number α,the net growth rate σ in the Floquet theory is only related to the Reynolds number Re. As shown in Fig. 1(a),which is for α = 0.3,the peak value of max|u| exhibits a net amplification at Re = 783,indicating the unstable mode of the Floquet theory. Similarly,the peak of max|u| experiences a net damping at Re = 780,which represents the stable mode. At Re = 781.4,the peak of max|u| is neither growing nor damping,corresponding to the global neutral mode. For α = 0.5,it is similar to the case of α = 0.3. The global neutral mode is found at around Re = 1 017,which can be observed in Fig. 1(b).

|
| Fig. 1 Evolution of max|u| |
|
|
Then,the neutral curve of the global instability in the α-Re plane can be obtained by this methodology for determining the neutral disturbances. Figure 2 shows the neutral curve at present and its comparison with the result of Ref. [7] by the Floquet theory. It can be seen that the present result agrees perfectly with the one in the pervious work,indicating that our methodology for obtaining the global instability is suitable.

|
| Fig. 2 Neutral curve of global instability in α-Re plane |
|
|
The above results indicate the evolution features for 0.2 < α < 0.5. Apparently,the neutral curve of global instability in this range of wave numbers can be obtained by the numerical simulation as well as solving the Floquet eigenvalue problem. However,for α < 0.2 and α > 0.5,the evolution behaviour is found to be quite different. Figure 3 shows the evolutions of the disturbances at α = 0.51 and α = 0.15,respectively. It can be found that the peak of max|u| appears twice in one cycle of base flow,no matter for α > 0.5 or α < 0.2. Moreover,the peaks display no monotonic development but the irregular fluctuations,not as expected by the Floquet theory. It is obvious that the assumption of the 2π-periodicity in the Floquet theory is irrelevant in these ranges of wave numbers. That is why the parts of global neutral curve for α > 0.5 and α < 0.2 cannot be obtained in the previous work.

|
| Fig. 3 Evolution of max|u| |
|
|
In order to interpret the above evolution characteristics,the disturbance with the large wave number (α > 0.5) is concerned below by the instantaneous theory,and a disturbance at α = 0.3 and Re = 780 is selected as a reference for the comparison. Figure 4(a) shows the instantaneous growth rates ωi(t) of the disturbance in one cycle,where the dashed black line represents the growth rates in the second half cycle. As illustrated in Fig. 4(a),the instantaneous growth rate ωi(t) replicates itself periodically for every π,due to the symmetry of the base flow in one cycle of base flow. For simplicity,the unstable mode which is generated in the first half cycle is called the mode 1,and the one which is generated in the second half cycle is called the mode 2. Figure 4(b) displays the eigenfunctions of the disturbance velocity u by the instantaneous theory at the typical time. According to the results of inviscid instability[3],the instantaneous growth rates can be divided into two distinct stages by the thick dashed line: the stage A and the stage B (marked in Fig. 4(a)). It can be seen in Fig. 4(a) that the stage A corresponds to the time interval 0 < t/(2π) < 0.25,and a disturbance in this stage exhibits a quick and transient growth. Moreover,the eigenfunction in the stage A is very close to the wall,which means that its effect on the whole flow is insignificant (see Fig. 4(b)). On the other hand,the stage B corresponds to the time interval t/(2π) > 0.25,and a disturbance in this stage exhibits a slow and continuous growth. Especially,when the Reynolds number is large enough,the unstable disturbance can be clearly examined in this stage. As found in Fig. 4(b),the eigenfunction in the stage B is far away from the wall,which indicates a significant effect on the whole flow.

|
| Fig. 4 Related results by instantaneous instability (α = 0.3 and Re = 780) |
|
|
Figure 5(a) displays the evolution of the disturbance velocity u over two cycles 0 ≤ t/(2π)≤2 at α = 0.3 and Re = 780,together with its instantaneous growth rates ωi(t) by the instantaneous theory. For the first cycle 0 ≤ t/(2π) ≤ 1,it can be clearly seen that the peak of max|u| experiences no decay until around t/(2π) = 0.6. Then,the disturbance keeps increasing till around t/(2π) = 1.4 where the flow enters the next cycle. It means that the maximum of the disturbance is dominated by the disturbances in the stage B which corresponds to the mode 1. Nevertheless,the mode 2 has experienced growth within the interval 0.53 < t/(2π) < 1.13,but is fully restrained and submerged because the mode 1 in this interval is still quite strong (see Fig. 5(a)). It is clearly observed that the mode 2 is only found at some specific times,such as t/(2π) = 2.0-2.4,t/(2π) = 3.0-3.4,but is restrained.

|
| Fig. 5 Evolution of disturbance velocity u for Re = 780 and α = 0.3 |
|
|
In order to further investigate the evolution behaviour of the mode 2,Fig. 6 shows the comparison of the normalized distribution of the disturbance |u| between the the local eigenfunctions by the linear instability theory (LIST) and the DNS at different time. As shown in Fig. 6,the numerical results are in excellent agreement with the local eigenfunctions. As the time t increases,the mode 1 gradually spreads away from the wall,but the mode 2 is found to concentrate in the wall region with the small amplitude. It means that there is only one peak in one cycle of base flow,which can be obviously observed.

|
| Fig. 6 Normalized distribution of disturbance |u| and comparison of DNS with LIST for α = 0.3 and Re = 780 |
|
|
However,it seems that the cases for α > 0.5 do not match the above discussion. The results of the case α = 0.51 and Re = 1 100 are selected as a typical example. Figure 7(a) shows the evolution of the disturbance and the instantaneous growth rates ωi(t). It can be seen that there is one peak of max|u| in every half cycle of the base flow instead of one cycle in the case α = 0.3. The mode 2 exhibits the rapid growth within the time interval 1 < t/(2π) < 1.4 and dominates the amplitude of the disturbance,i.e.,the first peak corresponds to the mode 1,the same as the case α = 0.3,and the second one corresponds to the mode 2. This phenomenon can also be easily seen form the contours of |u|(see Fig. 7(b)). It is obvious that the mode 2 has the same order of magnitude of the amplitude as the mode 1. It suggests that there is a “mode exchange” between the mode 1 and the mode 2 in one cycle of the base flow. Figure 8 displays the comparison of the normalized distribution of the disturbance |u| between the DNS and the LIST for α = 0.51 and Re = 1 100. The “mode exchange” can be clearly observed. The numerical results indicate that the mode 1 dominates the disturbance within the interval 0.8 < t/(2π) < 0.9 while the mode 2 exhibits the rapid growth and then becomes the dominant mode within 0.9 < t/(2π) < 1. However,the LIST results still suggest that the disturbance is dominated by the mode 1,and the mode 2 is not amplified. The divergence between the DNS and the LIST results may cause some confusions.

|
| Fig. 7 Evolution of disturbance velocity u for Re = 1 100 and α = 0.51 |
|
|

|
| Fig. 8 Normalized distribution of disturbance |u| and comparison of DNS with LIST for α = 0.51 and Re = 1 100 |
|
|
Actually,during the process of the“mode exchange” between the mode 1 and the mode 2,it is noted that the mode 2 is amplified by the projection of the mode 1 in the temporal direction. The mode 1 dominates the disturbance far away from the wall,and the disturbance close to the wall is very small. In contrast,the mode 2 dominates the disturbances close to the wall. Then,during the time interval of “the mode exchange”,it is a randomness that the decaying disturbances at the first half cycle project to the modes at the latter half cycle. This randomness induces the irregularity of the evolution in the whole cycle. Especially,when the disturbance is approximately neutral,this irregularity is quite significant,and then the evolution of disturbances is aperiodicity in the microscopic,which causes the failure of the global instability analysis.
The above results concentrate on the cases of α > 0.5. Actually,the characteristics of the evolution of the disturbances for α < 0.2 are quite similar. Therefore,the related results at small wave numbers are not given at present.
3.3 New definition of neutral pointAlthough the evolution of the disturbance is aperiodicity for α < 0.2 and α > 0.5,it is hoped that the instability of the flow can be obtained in this range. It is found that the peak value of max|u| is irregular only in a rather limited range of Reynolds numbers,outside of which the peak of max|u| exhibits the obvious growth or decay. Figure 9 shows the evolutions of the disturbances at α = 0.51 for different Reynolds numbers. It can be seen that the peak of max|u| exhibits the net decay for 1 080 < Re < 1 090 and the obvious global growth for 1 120 < Re < 1 130. It means that the irregularity of the global instability occurs only in a narrow range 1 090 < Re < 1 120 for α = 0.51. Therefore,the neutral is defined by a range of the Reynolds number rather than a given value,called “the range of approximately neutral Reynolds number”. For α = 0.51,this range is Re = 1 090-1 120. The similar phenomenon occurs at other wave numbers,such as α = 0.55,0.6,and 0.7. More results for α > 0.5 are displayed in Fig. 10,and the range of the approximately neutral Reynolds number can also be determined. As found,these ranges are 1 180 < Re < 1 220 for α = 0.55,1 340 < Re < 1 360 for α = 0.6,and 2 000 < Re < 2 040 for α = 0.7,respectively. It is obvious that these ranges are all quite narrow.

|
| Fig. 9 Evolutions of max|u| for α = 0.51 |
|
|

|
| Fig. 10 Evolutions of max|u| for (a)−(c) α = 0.55, (d)−(f) α = 0.6, and (g)−(i) α = 0.7 |
|
|
Similarly,the range of approximately neutral Reynolds number also can be found at α < 0.2. Figure 11 shows the evolutions of the disturbances at α = 0.1 and α = 0.15. It is easily found that these ranges are 3 200 < Re < 3 280 for α = 0.1 and 1 900 < Re < 1 960 for α = 0.15,respectively.

|
| Fig. 11 Evolutions of max|u| for (a)−(c) α = 0.1 and (d)−(f) α = 0.15 |
|
|
According to the concept of the range of approximately neutral Reynolds number,the theoretical neutral curve of the global instability can be expanded to the range of wave numbers 0.1 < α < 0.7. In order to prolong the above range of wave numbers,the instantaneous instability must be analyzed. Figure 12 shows the neutral curves of instantaneous instability at Re = ∞ and Re = 780. It can be seen that the unstable region can be divided into two stages: the stage A and the stage B. As found,the maximum and minimum wave numbers of the region A are related to the Reynolds number. For Re = ∞,this maximum value approximates α = 1.5,and the minimum value approximates zero. On the contrary,the maximum and the minimum wave numbers of the stage B are found to be independent of Re. The maximum one is about α = 0.8,and the minimum one always approximates zero. Moreover,it also can be seen that the unstable region of the stage B is limited but greater than one half of the cycle of base flow in the temporal scale at a small Reynolds number. As Re increases,the stage B will last for a quite long time.

|
| Fig. 12 Neutral curve of instantaneous instability in α-t plane |
|
|
As discussed in Subsection 3.2,the global growth of the disturbance is mainly dependent on the stage B. When α > 0.8,the disturbance displays the instability only in the stage A,and the amplification window is only in the interval 0.12 < t/(2π) < 0.22,i.e.,the growth of the disturbance is transient,indicating the strong intermittence of the disturbances. This is shown in Fig. 12. Therefore,the wave number α = 0.8 is a dividing line of the evolution of the disturbances. Figure 13 shows the evolutions of the disturbances at α = 0.76,0.78,and 0.8,respectively. When α = 0.76,there are two peaks in one cycle,indicating that the evolution behaviour of the disturbances is quite similar to the one for lower wave numbers,such as α = 0.51. However,many “spikes” can be observed at the specific time in the evolution (see Fig. 13(a)). These “spikes” are induced by the transient growth in the stage A. As the wave number α increases,the amplification rate of the stage B becomes even smaller. As a result,the main peak of the disturbance becomes smaller,and the spikes become more significant. When α = 0.78,these spikes are much higher than the main peaks because the contribution of the stage B on the disturbance amplitude is quite small. When the wave number α increases to 0.8,as shown in Fig. 13(c),only the spikes can be observed in the evolution of the disturbance. It means that the amplification window of the stage B is closed,and the disturbance only exhibits the transient growth in the stage A. Then,the disturbances are very sensitive to the external factors,such as the Reynolds number and the initial condition. Figure 14 shows the contours of |u| in the y-t plane for α = 0.8. As found,the disturbances exhibit the transient growth only in the stage A and the decay in the most time,indicating the quite significant intermittence.

|
| Fig. 13 Evolutions of max|u| for α > 0.75 |
|
|

|
| Fig. 14 Contours of |u| in y-t plane for α = 0.8 |
|
|
According to the neutral curve of the instantaneous instability,the disturbance is intermittent at 0.8 < α < 1.5,and the significant spikes can be observed in the flow. As the wave number increases,the amplitude of the spikes is damping. When α > 1.5,even the stage A is closed,indicating that no unstable disturbance can be found in the flow.
In summary,the neutral curve of global instability of the Stokes layer can be obtained (see Fig. 15),and it can be divided into five parts with four different characteristics. (Ⅰ) 0.2 < α < 0.5,the peak of the disturbance amplitude exhibits the exponential evolution,and the eigenfunction displays the periodicity,indicating the Floquet mode; (Ⅱ) 0 < α < 0.2 and 0.5 < α < 0.8,there are two peaks of the disturbance which can be found,and the evolution of the disturbance is not monotonous in a narrow Reynolds number range. Outside this range,the growth and the decay of the disturbances are quite clear. Then,this narrow range can be defined as the range of approximately neutral Reynolds numbers to determine the global neutral curve; (Ⅲ) 0.8 < α < 1.5,only the amplification window of the stage A is left,inducing the significant intermittence of the evolution; (Ⅳ) α > 1.5,all disturbances are globally stable.

|
| Fig. 15 Neutral curve of global instability for all wave numbers, where solid line is from Ref. [7], and symbols represent present results from numerical simulation, triangle symbols represent approximately critical Reynolds number Rec, and dashed points display intermittent region |
|
|
The Stokes layer is a classical model for investigating the instability of the unsteady flows. The traditional Floquet approach only gives the neutral curve of the global instability in a rather limited range of wave numbers,0.2 < α < 0.5. In this paper,the linear evolution of disturbances in an infinite Stokes layer is investigated numerically by invoking the instantaneous instability theory. The results indicate that the disturbances at large wave numbers (α > 0.5) and small wave numbers (α < 0.2) will display the irregular evolution. That is why the previous studies fail to seek the neutral point in these ranges of wave numbers. Moreover,the concept of “the range of approximately neutral Reynolds number” is introduced to delineate the evolution behaviour,and the neutral curve of the global instability is obtained to include the added portion by the new definition. It suggests that the neutral curve of the global instability of the Stokes layer can be divided into five regions:
(i) For 0 < α < 0.2,the evolution of the peak of the disturbances is irregular and nonmonotonic near “the range of approximately neutral Reynolds number”. Although the traditional Floquet theory cannot be used in this region,the neutral curve can be identified by the new definition.
(ii) For 0.2 < α < 0.5,the disturbance exhibits the evolution by the Floquet mode,and the normal distribution of disturbance displays the periodicity,then,the neutral curve of global instability can be obtained in this range of wave numbers.
(iii) For 0.5 < α < 0.8,the characteristics are nearly the same as the region (i),expect some “spikes” appearing at the large wave numbers.
(iv) For 0.8 < α < 1.5,the main peak of the evolution of the disturbances is insignificant. The evolution of the disturbances demonstrates the strong intermittence,indicating that the results are very sensitive to the numerical method,initial condition,etc.
(v) For α > 1.5,there is no unstable disturbance at any time,indicating the global stability of the flow.
The present work dispels the puzzle in the global instability of the Stokes layer and provides a deeper understanding of the global instability of the unsteady flow.
| [1] | Collins, J. I. Inception of turbulence at the bed under periodic gravity waves. J. Geophys. Res., 68, 6007-6014 (1963) |
| [2] | Davis, S. H.and von Kerczek C. A reformulation of energy stability theory. Arch. Rat. Mech. Anal., 52, 112-117 (1973) |
| [3] | Cowley, S. J. High frequency Rayleigh instability of Stokes layers. Stability of Time-Dependent and Spatially Varying Flows (eds. Dwoyer D. L., 1987, Hussaini M. Y..). Springer, New York, 261-275 (1987) |
| [4] | Von Kerczek, C., & Davis, S. H. Linear stability theory of oscillatory Stokes layers. J. Fluid Mech., 62, 753-773 (1974) |
| [5] | Hall, P. The linear instability of flat Stokes layers. J. Fluid Mech., A359, 151-166 (1978) |
| [6] | Akhavan, R., Kamm, R. D., & Shapiro, A. H. An investigation of transition to turbulence in bounded oscillatory Stokes flows:numerical simulations. J. Fluid Mech., 225, 423-444 (1991) |
| [7] | Blennerhassett, P. J., & Bassom, A. P. The linear stability of flat Stokes layers. J. Fluid Mech., 464, 393-410 (2002) |
| [8] | Hall, P. On the instability of Stokes layers at high Reynolds numbers. J. Fluid Mech., 482, 1-15 (2003) |
| [9] | Blennerhassett, P. J., & Bassom, A. P. The linear stability of high-frequency oscillatory flow in a channel. J. Fluid Mech., 556, 1-25 (2006) |
| [10] | Luo, J., & Wu, X. On the linear stability of a finite Stokes layer:instantaneous versus Floquet modes. Phys. Fluids, 22, 1-13 (2010) |
| [11] | Thomas, C., Bassom, A. P., Blennerhassett, P. J., & Davies, C. Direct numerical simulations of small disturbances in the classical Stokes layer. J. Eng. Math., 68, 327-338 (2010) |
| [12] | Thomas, C., Bassom, A. P., & Blennerhassett, P. J. The linear stability of oscillating pipe flow. Phys. Fluids, 24, 1-10 (2012) |
| [13] | Thomas, C., Davies, C., Bassom, A. P., & Blennerhassett, P. J. Evolution of disturbance wavepackets in an oscillatory Stokes layer. J. Fluid Mech., 752, 543-571 (2014) |
| [14] | Thomas, C., Bassom, A. P., Blennerhassett, P. J., & Davies, C. The linear stability of a Stokes layer subjected to high-frequency perturbations. J. Fluid Mech., 764, 193-218 (2015) |
| [15] | Hino, M., Sawamoto, M., & Takasu, S. Experiments on transition to turbulence in an oscillatory pipe flow. J. Fluid Mech., 75, 193-207 (1976) |
| [16] | Hino, M., Kasguwayanagi, M., Nakayama, A., & Hara, T. Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow. J. Fluid Mech., 131, 363-400 (1983) |
| [17] | Jensen, B. L., Sumer, B. M., & Fredsoe, J. Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech., 206, 265-297 (1989) |
| [18] | Akhavan, R., Kamm, R. D., & Shapiro, A. H. An investigation of transition to turbulence in bounded oscillatory Stokes flows:experiments. J. Fluid Mech., 225, 395-422 (1991) |
| [19] | Malik, M. R. Numerical methods for hypersonic boundary layer stability. J. Comput. Phys., 86, 376-413 (1990) |
 2016, Vol. 37
2016, Vol. 37











