Shanghai University
Article Information
- R. KANDASAMY, R. MOHAMMAD, I. MUHAIMIN
- Carbon nanotubes on unsteady MHD non-Darcy flow over porous wedge in presence of thermal radiation energy
- Applied Mathematics and Mechanics (English Edition), 2016, 37(8): 1031-1040.
- http://dx.doi.org/10.1007/s10483-016-2115-8
Article History
- Received May. 1, 2015
- Revised Apr. 6, 2015
The thermal radiation energy has been receiving more and more attention as governments are trying to shift from fossil fuel-based energy sources to more natural and renewable options. Nanofluidsengineered colloidal suspensions of nanoparticles in a base fluid are attracting a great deal of interest with their enormous potential to provide enhanced performance properties. Particularly,with respect to heat transfer,and compared with more conventional heat transfer fluids (i.e.,coolants) currently available,nanofluidic coolants exhibit the enhanced thermal conductivity. Attempts to increase the thermal conductivity of heat transfer fluids using nanoparticles have been an active research area over the past decade. However,these attempts have not resulted in a significant improvement in the conductivity due to the low thermal conductivity of nanoparticles and high thermal boundary resistance around the zero-dimensional nanoparticles. Therefore,the present paper decides to produce a nanofluid using single-walled carbon nanotubes (SWCNTs) because of their much higher thermal conductivity and their ability to form connected networks with the neighboring carbon nanotubes (CNTs),thereby increasing the heat transfer path. Lalwani et al.[1],Nield and Kuznetsov[2],Kuznetsov and Nield[3],and Khan and Pop[4] found that their SWCNT nanofluid exhibits an increase in the conductivity of up to almost 15%,a value significantly larger than what has been achieved with nanoparticle-based nanofluids. A CNT is a tube-shaped material,made of carbon,having a diameter measuring on the nanometer scale. CNTs have many structures,differing in the length,thickness,and in the type of helicity and the number of layers. SWCNTs have unique electronic and mechanical properties which can be used in numerous applications,such as field-emission displays,nanocomposite materials,nanosensors,and logic elements. These materials are on the leading-edge of electronic fabrication,and are expected to play a major role in the next generation of miniaturized electronics. Wang and Zhao[5] investigated that the slip boundary conditions were based on the kinetic theory and molecular dynamic simulations. The results predicted that the momentum transfer among the liquid layers and the bulk liquid must be considered according to the wetting conditions of the solid surface,which can interpret the contradictory published results of slip behavior at the high shear stress. Although the atomic density profile differs with the tube diameter,reflecting the change in the static microscopic structure of flow from the single file to the cylindrical tube,the tube diameter does not give a clear transition in the streaming velocity,temperature,or hydrogen bond lifetime over this diameter range. The results suggest that the water flow in CNTs of this size is more plug-like than the Poiseuille type,although the flow model/structure does not strictly depend on either plug-like or Poiseuille type.
Multi-walled carbon nanotubes (MWCNTs) consist of multiple rolled layers (concentric tubes) of graphene. Because of the statistical probability and restrictions on the relative diameters of the individual tubes,one of the shells,the whole MWCNT,is usually a zero-gap metal. Double-walled carbon nanotubes (DWCNTs) form a special class of nanotubes because their morphology and properties are similar to those of SWCNTs but their resistance to chemicals is significantly improved. This is especially important when the functionalization is required (this means grafting of chemical functions at the surface of the nanotubes) to add new properties to the CNT. In the case of SWCNTs,the covalent functionalization will break some carbon double bonds,leaving “holes” in the structure on the nanotube,thus modifying both mechanical and electrical properties. In the case of DWCNTs,only the outer wall is modified. The telescopic motion ability of inner shells and their unique mechanical properties will permit the use of multi-walled nanotubes as main movable arms in coming nanomechanical devices[6]. The retraction force occurs due to the telescopic motion caused by the Lennard-Jones interaction between shells,and its value is about 1.5 nN[7].
Yuan and Zhao[8-9] studied that the transport properties of confined water in an SWCNT are different from those of the bulk water in view of the configuration,the diffusion coefficient,the dipole orientation,and the density distribution. A voltage difference of several millivolts could be generated between the two ends of an SWCNT due to interactions between the water dipole chains and charge carriers in the tube. Hence,the structure of a water-filled SWCNT can be a dominant candidate for a synthetic nanoscale power cell as well as a practical nanopower harvesting device.
Based on the aforementioned introduction,it could be stated that little published literature exists regarding SWCNTs in water and their applications as the heat transfer fluid. Also,there is the inconsistency in the few reported studies on the convective heat behavior of CNT-nanofluids. Therefore,it was decided to study the convective heat transfer behavior of SWCNTs in water in laminar flow regimes.
2 Mathematical analysisLet us consider an unsteady laminar two-dimensional non-Darcy flow of an incompressible viscous nanofluid past a porous wedge in the presence of solar energy radiation (see Fig. 1). The fluid is a water based the nanofluid containing copper nanoparticles and SWCNTs. The working fluid is assumed to have heat absorption properties,and the porous medium absorbs the incident thermal radiation energy and transits it to the working fluid by convection. The thermophysical properties of the nanofluids are given in Tables 1−3. Under the same assumptions of Ref. [10],the boundary layer equations governing the flow and thermal field can be written in the dimensional form of
where 

|
| Fig. 1 Physical flow model over porous wedge sheet |
|
|
The boundary conditions of these equations are
where c1 and n1 (power index) are constants,and v0 and Tw are the suction ( > 0) or injection ( < 0) velocity and the fluid temperature at the plate,respectively. The potential flow velocity and the angle of the wedge can be written as 


In the limit of low particle volume concentration ϕ,the nanoparticle conductivity ks is much larger than the base liquid conductivity kf. μf is the viscosity of base fluid,ϕ is the nanoparticle fraction,(ρcp)nf is the effective heat capacity of a CNT,knf is the thermal conductivity of nanofluid,kf and kCNT are the thermal conductivities of the base fluid and CNT,respectively,while ρf and ρCNT are the thermal conductivities of the base fluid and CNT,respectively.
Following the lines of Ref. [13],the changes of variables are
By introducing the stream function ψ,defined as 

and the boundary conditions take the following form:
where 














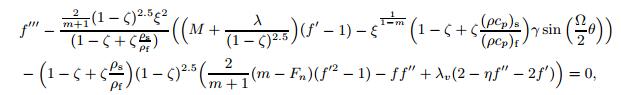 (10)
(10) 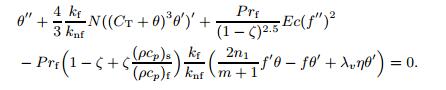 (11)
(11) The boundary conditions take the following form:
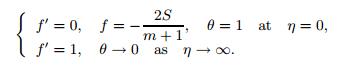 (12)
(12) Further,we suppose that 



For practical purposes,the functions f(η) and θ(η) allow us to determine the skin friction coefficient,
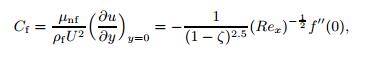 (13)
(13) and the Nusselt number
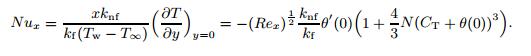 (14)
(14) Here,Rex = Ux νf is the local Reynolds number.
3 Results and discussionThe systems of Eqs. (10) and (11) are highly nonlinear coupled equations and cannot be solved analytically,and numerical solutions subject to the boundary conditions (12) are obtained by the very robust computer algebra software MAPLE 18. This software uses a fourth-fifth order Runge-KuttaFehlberg method as default to solve the boundary value problems numerically using the DSOLVE command. The numerical results are represented in the form of the dimensionless velocity and temperature in the presence of the SWCNT and copper nanoparticles.
Figure 2 presents typical profiles for velocity and temperature for different materials (Titania,Alumina,silver,copper,and SWCNTs) in the presence of base fluid (water). Due to the uniform convective radiation,it is clearly shown that the velocity and the temperature of the nanofluid accelerate with the increase of the water based nanoparticles (Titania,Alumina,silver,copper,and SWCNTs). It is observed that the temperature for water based SWCNTs is higher than that of other nanoparticles,which implies that the SWCNTs show a unique combination of stiffness,strength,and tenacity compared to other fiber materials which usually lack one or more of these properties. Thermal conductivity and electrical conductivity of SWCNTs are also very high,compared with other conductive materials. The increase of thermal boundary layer field due to the increase in the thermal conductivity shows that the temperature field increases gradually as we replace Titania by Alumina,silver,copper,and SWCNTs in the said sequence.

|
| Fig. 2 Effects of water based SWCNTs and nanoparticles on velocity and temperature profiles |
|
|
Figures 3 and 4 illustrate the characteristic velocity and temperature profiles for different values of the convective radiation N and nanoparticle volume fraction ζ in the presence of water based copper nanoparticles and SWCNTs. In both cases,it is noticed that the temperature of the nanofluid increases with the increase of the convective radiation and nanoparticle volume fraction parameters. It is also observed that the temperature for water based SWCNTs is stronger than that of copper nanofluid,because the combined effect of the thermal conductivity/density of the SWCNTs is stronger/weaker compared to the copper nanoparticles in the base fluid,respectively. From Figs. 5-9,it is predicted that the water based SWCNTs plays a dominant role on velocity and temperature profiles compared with the copper nanofluid with the increase of all the other parameters in this investigation. SWCNTs are expected to be very good thermal conductors along the tube,exhibiting a property known as “ballistic conduction”,and good insulators laterally along the tube axis. Measurements show that the water based SWCNT has a room-temperature thermal conductivity along its axis of about 3 500 W·m−1·K−1. Eric et al.[16] compared this with copper nanoparticles,a metal well known as its good thermal conductivity,which transmits 385 W·m−1·K−1. The strength and flexibility of SWCNTs make them of potential use in controlling other nanoscale structures,which suggests that they will have an important role on the renewable (solar) energy technology. The enhancement in the thermal conductivity of SWCNTs can lead to efficiency improvements,although small,via the more effective fluid heat transfer. In the convective heat transfer of the nanofluid,the heat transfer depends not only on the thermal conductivity but also on other properties,such as the specific heat,density,and dynamic viscosity of the nanofluid (water based SWCNTs). Changes in the size,shape,material,and volume fraction of the SWCNTs allow for tuning to maximize the spectral absorption of solar energy throughout the fluid volume,because the nanoparticle volume fraction parameter depends on the size of the particles. The enhancement in the thermal conductivity water based SWCNTs can lead to efficiency improvements,although small,via the more effective fluid heat transfer. From Fig. 10,it is found that the temperatures of water based SWCNTs and MWCNTs increase with the increase of thermal radiation but there is no significant difference between the temperature profiles. It is also observed that the rate of heat transfer for SWCNTs-water and MWCNTs-water decreases with the increase of thermal radiation (see Table 4).

|
| Fig. 3 Effects of convective radiation on velocity and temperature profiles |
|
|

|
| Fig. 4 Effects of nanoparticle volume fraction on velocity and temperature profiles |
|
|

|
| Fig. 5 Effects of magnetic strength on velocity and temperature profiles |
|
|

|
| Fig. 6 Effects of suction on velocity and temperature profiles |
|
|

|
| Fig. 7 Effects of Forchheimer number on velocity and temperature profiles |
|
|

|
| Fig. 8 Effects of porosity on velocity and temperature profiles |
|
|

|
| Fig. 9 Effects of unsteady parameter on velocity and temperature profiles |
|
|

|
| Fig. 10 Effects of thermal radiation on temperature profiles |
|
|

|
The thermal boundary layer thickness of water based SWCNTs is larger than that of the copper nanofluid as the strength of the convective radiation and the nanoparticle volume fraction increases because CNTs experience an increase in the temperature after being heated by the thermal radiation energy. It is observed that the temperature of water based SWCNTs is accelerated monotonically with the increase of convective radiation as compared with that of the copper nanofluid. It has been shown that mixing SWCNTs in a base fluid (water) has a dominant effect on the liquid thermophysical properties while the thermal conductivity of the water based SWCNTS is strongly dependent on the nanoparticle volume fraction. SWCNTs in the presence of base fluid flow over a porous wedge play a significant role on absorbing the incident solar radiation and transiting it to the working fluid by convection. It is interesting to note that the thermal boundary layer thickness for SWCNTs-water is significantly larger with the increase of thermal radiation,nanoparticle volume fraction,and unsteady parameters as compared with Cu-water because of the combined effects of thermal conductivity,diffusivity,size,and shape of the nanoparticles and CNTs. The strength of rate of heat transfer for MWCNTs-water is significantly larger than that of SWCNTs-water in the presence of thermal radiation energy due to the joined effects of specific heat with the thermal expansion and conductivity of MWCNTs. Water based SWCNTs have been proven to be excellent thermal and electrical conductors that can be used in the thermal radiation energy technology because the thermal conductivity of SWCNTs is significantly better than that of copper nanoparticles.
Acknowledgement The authors wish to express their cordial thanks to our beloved Vice Chancellor and Dean of Universiti Tun Hussein Onn Malaysia for their encouragements and acknowledge the financial support received from FRGS 1208/2013.| [1] | Lalwani, G., Kwaczala, A. T., Kanakia, S., Patel, S. C., Jude, S., & Sitharaman, B. Fabrication and characterization of three-dimensional macroscopic all-carbon scaffolds. Carbon, 53, 90-100 (2013) |
| [2] | Nield, D. A., & Kuznetsov, A. V. The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heat and Mass Transfer, 52, 792-795 (2009) |
| [3] | Kuznetsov, A. V., & Nield, D. A. Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 49, 243-247 (2010) |
| [4] | Khan, W. A., & Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer, 53, 2477-2483 (2010) |
| [5] | Wang, F. C., & Zhao, Y. P. Slip boundary conditions based on molecular kinetic theory:the critical shear stress and the energy dissipation at the liquid-solid interface. Soft Matter, 7, 8628-8634 (2011) |
| [6] | Reacy, M. M. J., Ebbesen, T. W., & Gibson, J. M. Exceptionally high Young's modulus observed for individual carbon nanotubes. Nature, 381, 678-680 (1996) |
| [7] | Zavalniuk, V., & Marchenko, S. Theoretical analysis of telescopic oscillations in multi-walled carbon nanotubes. Low Temperature Physics, 37, 337-343 (2011) |
| [8] | Yuan, Q. Z., & Zhao, Y. P. Transport properties and induced voltage in the structure of waterfilled single-walled boron-nitrogen nanotubes. Biomicrofluidics, 3, 022411 (2009) |
| [9] | Yuan, Q. Z., & Zhao, Y. P. Hydroelectric voltage generation based on water-filled single-walled carbon nanotubes. Journal of the American Chemical Society, 131, 6374-6376 (2009) |
| [10] | Kandasamy, R., Muhaimin, I., & Rosmila, A. K. The performance evaluation of unsteady MHD non-Darcy nanofluid flow over a porous wedge due to renewable (solar) energy. Renewable Energy, 64, 1-9 (2014) |
| [11] | Sparrow, E. M. and Cess, R. D. Radiation Heat Transfer, McGraw Hill Higher Education, Washington, D. C. (1978) |
| [12] | Sattar, M. A. Local similarity transformation for the unsteady two-dimensional hydrodynamic boundary layer equations of a flow past a wedge. International Journal of Applied Mathematics and Mechanics, 7, 15-28 (2011) |
| [13] | Kafoussias, N. G., & Nanousis, N. D. Magnetohydrodynamic laminar boundary layer flow over a wedge with suction or injection. Canadian Journal of Physics, 75, 733-741 (1997) |
| [14] | Kandasamy, R., Loganathan, P., & Arasu, P. P. Scaling group transformation for MHD boundary-layer flow of a nanofluid past a vertical stretching surface in the presence of suction/injection. Nuclear Engineering and Design, 241, 2053-2059 (2011) |
| [15] | Schlichting, H. and Gersten, K. Boundary-Layer Theory, McGraw Hill, New York (1979) |
| [16] | Eric, P., David, M., Qian, W., Kenneth, G., & Hongjie, D. Thermal conductance of an individual single-wall carbon nanotube above room temperature. Nano Letters, 6, 96-100 (2005) |
 2016, Vol. 37
2016, Vol. 37
















