Shanghai University
Article Information
- Jiusheng REN, Chengmin WANG
- Electromechanical responses and instability of electro-active polymer cylindrical shells
- Applied Mathematics and Mechanics (English Edition), 2016, 37(8): 1067-1076.
- http://dx.doi.org/10.1007/s10483-016-2118-9
Article History
- Received Sep. 18, 2015
- Revised Mar. 4, 2016
2. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
Electro-active polymers (EAPs) have many excellent mechanical properties in electric fields,such as large strain,fast response,and energy conversion efficient[1-2]. Along with their excellent characteristics,these polymers are lightweight,flexible,pliable,and cheap,which make them the preferred materials for transducers and artificial muscles[3]. These kinds of materials can be made into actuators,sensors,and energy collectors,and they play an important role in robotics,space technology,biomedical,energy harvesting field,and so on[1-3].
Research efforts are being put forward to correct the failures of electricity polymers associated with their wide-spread application[4]. It is found that dielectric elastomers actuators (DEAs) fail easily,which negatively affects their application[5]. An ideal DEA model was proposed to describe how the actuator fails[5]. In recent years,methods to study the electrical and mechanical stability of dielectric polymers were developed[6-8]. The dielectric polymers may produce electromechanical instability if the Hessian matrix of the free energy function is definite positive[7]. The instability of an EAP cylindrical shell under the static and dynamic voltage was studied[9-10],and the unstable deformation of EAP shells was observed in experiments[11-12]. There exists a critical voltage,and the EAP shell may be destructed when the voltage is greater than this critical value. One method for analyzing the stability of dielectric elastomers with the electromechanical coupling theory was explored by Liu et al.[13].
In this paper,electromechanical responses and the instability of an incompressible EAP cylindrical shell which is subjected to an internal pressure and a static electric field are studied. First,the control equation based on the finite deformation theory of elasticity is derived,and then the deformation curves and the distribution of stresses are obtained. The critical pressure,the critical thickness,and the critical voltage are given. The effects of the electric field,the axial stretch,and the thickness on the instability are discussed through exploring the deformation curves.
2 BasicequationsConsider a finite deformation cylindrical shell made of an incompressible dielectric elastomer with the inner radius A,the outer radius B,and the length L. Both the inner and outer surfaces of the shell are covered with thin electrodes with the negligible elastic modulus. With these electrodes,an electric field is induced across the wall. The shell may be inflated with an internal pressure p and electrically exited with the electric potential Φ between the two electrodes. The inner and outer radii turn into a and b separately,and the length changes into l. The cylindrical coordinates systems (R,Θ,Z) and (r,θ,z) with the co-origin at the center of the shell are used to describe the undeformed and the deformed configurations. Assume that the deformation function of the cylindrical shell is axially symmetric,namely,
where λz is the axial stretch. The corresponding deformation gradient tensor is
As the material is incompressible,
The principal stretch ratios are
Following the theory of the nonlinear electro-elasticity,the strain energy function of an ideal dielectric elastomer is introduced[14-15],
Here,the first part is the elastic strain energy,and the second part is the electrostatic energy induced by the electric field. D is the electric displacement in the radial direction,and ε is the permittivity of the elastomer. For common polymers,ε = 2.21×10−11 F/m[10]. Typical values of the elastic constants are[15]
The total non-zero stresses consist of the Cauchy stress and the Maxwell stress,i.e.,
where P(R) is the hydrostatic pressure to be determined. D = Q/(2πrλzL) is the radial electric displacement,in which Q is the electric charge. The electric voltage ϕ is
Here and thereafter,
The equilibrium equation of the shell in the absence of body forces is
The associated boundary conditions are
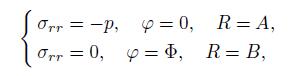 (10)
(10) where Φ is the electric voltage subjected between the two electrodes on the surfaces of the shell.
3 olutions and resultsIn order to seek the solutions,substituting Eq. (6) into Eq. (9),with the variable transformation r(R) = Rv(R),the equilibrium equation may be rewritten as
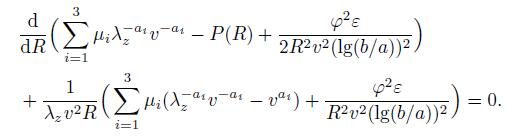 (11)
(11) Integrating Eq. (11),we have
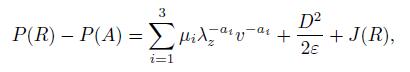 (12)
(12) where
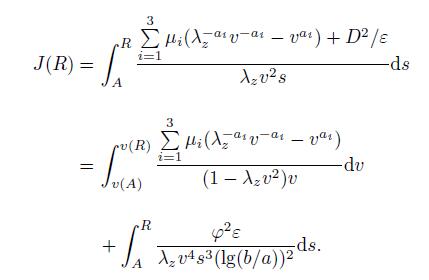 (13)
(13) Substituting Eqs. (12) and (13) into Eq. (10) yields
Then,
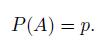 (14)
(14) Substituting Eq. (14) into Eq. (6) yields
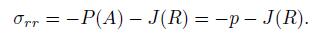 (15)
(15) Substituting Eq. (15) into Eq. (10) yields
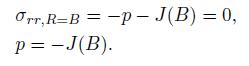 (16)
(16) Then,we have
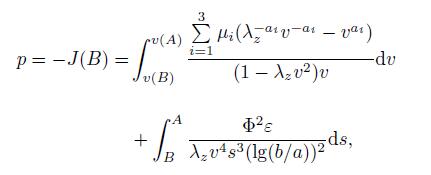 (17)
(17) where
λ = v(A) is used to express the corresponding deformation of the inner surface of the shell.
η = A/B is the ratio of the undeformed radii. The deformation of the external surface may be described as
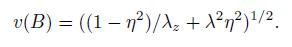 (18)
(18) The total stresses may be written as
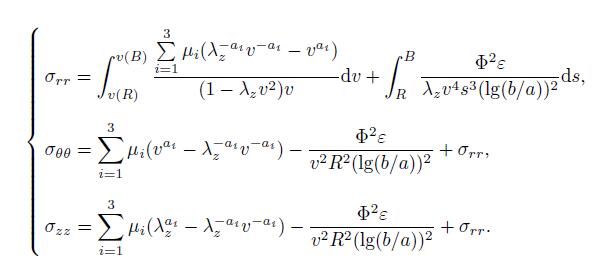 (19)
(19) For given values of the internal pressure and the electric voltage,exact values for the deformation of the shell may be obtained from Eq. (17),and the deformation of the shell may be described. The deformation curves of thin-walled shells,thick-walled shells,a thin-walled shell with different axial stretches,and a thin-walled shell with changing voltages are shown in Fig. 1. The deformation curves of a thin-walled shell with different voltages are shown in Fig. 2.

|
| Fig. 1 Deformation curves of thick-walled shells,thin-walled shells,thin-walled shell with different axial stretches,and thin-walled shell with changing voltages |
|
|

|
| Fig. 2 Deformation curves of thin-walled shell with positive and negative voltages |
|
|
For a thin-walled shell,the deformation curves of the shell are not monotonic,and there exists a maximum internal pressure pmax. When the internal pressure p is less than the maximum pressure pmax,the shell slowly expands with the increase of the inflation pressure. However,the deformation of the shell keeps increasing even if the pressure decreases when the internal pressure p is larger than the maximum pressure pmax. It suggests that the further increase of the pressure will lead to a sudden jump in the size of the shell in a certain place after the critical pressure is reached. After this “snap-through” phenomenon,the shell will get a second stable deformation state. Then,the further increase of the size of the shell will need further increase of the pressure.
It is also shown that it is easier for a thinner thin-walled shell to have an unstable deformation than a thicker one. Both the increases of the thickness and the axial stretch lead to the increases of the critical pressure pmax and the deformation λ which corresponds to the critical pressure. While for a thick-walled shell,the deformation always increases with the increase of the internal pressure. The deformation curve is always monotonic,and there is no unstable deformation for a thick-walled shell.
It is shown in Fig. 1(d) that there exists a maximum voltage Φmax on the deformation curve for the deformation versus the voltage of a thin-walled shell. Under a fixed pressure,the shell slowly expands with the increases of the voltage until a critical voltage Φmax is reached. The further increase in the voltage leads to a sudden jump in the size of the shell to a second stable state. When the voltage Φ is smaller than Φmax,the shell has a stable deformation. However,when the voltage Φ is larger than Φmax,the shell has an unstable deformation.
As it is shown in Fig. 2,for a thin-walled shell,the maximum pressure pmax decreases with the increase of the absolute value of the voltage. The curve of the critical pressure versus the voltage for a thin-walled shell is shown in Fig. 3. It is shown that the decrease of the maximum pressure pmax with the increase of the electric potential is nonlinear. This implies that the greater the voltage is,the more easily the shell is to be destructed.

|
| Fig. 3 Deformation curves of thin-walled shell with positive and negative voltages |
|
|
The results for the distribution of stresses of the shell obtained from Eq. (19) are shown in Fig. 4. It is shown that the absolute value of the radial stress decreases in the radius direction. It is zero at the outer surface,while it reaches the maximum value at the inner surface. The hoop stress and the axial stress decrease with the increase of the radius. Their maximum values occur at the inner surface. At the same time,all the stress components increase with the increase of the internal pressure or the voltage.

|
| Fig. 4 Distribution of radial stress,hoop stress,and axial stress of shell with different pressures |
|
|
From the above,the shell with different thicknesses may get different kinds of deformation. The thin-walled shell may get an unstable deformation,while there is no unstable deformation for the thick-walled shell. Thus,it is necessary to get the critical thickness of shell for the unstable deformation.
According to the deformation curves,there are non-monotonic curves for the unstable deformation. The relation between the pressure p and the deformation λ given by Eq. (17) should be non-monotonic. Assume that the general strain energy function is W = W(v). Hence,Eq. (17) may be written as
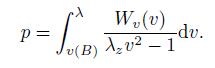 (20)
(20) The slope of the stress-strain curve at the internal surface is
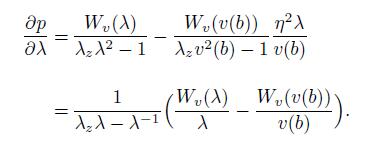 (21)
(21) According to Eq.(21),if Wv/v is a non-monotonic function of v,p is also a non-monotonic function of λ. Substituting the total strain energy function (5) into Wv/v,the (Wv/v)-v curve is shown in Fig. 5.

|
| Fig. 5 (Wv/v)-v curve |
|
|
As it is shown in Fig. 5,it is a non-monotonic curve actually. For the unstable deformation,λ is v2 = 3.5 (Φ = 1×105 V). Another point on the left of the same pressure is with a deformation value v1 = 1.47. Then,substitute λ = v2 = 3.5 and v(B) = v1 = 1.47 into Eq. (18). We have
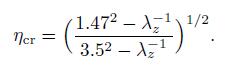 (22)
(22) It is shown in Eq. (22) that the critical thickness of a shell which may get an unstable deformation is determined when the axial stretch ratio is given. It is shown by the results that this critical thickness increases with the increase of the axial stretch ratio. When the thickness of the shell is smaller than this critical thickness,there may be an unstable deformation. For example,we get ηcr = 0.32 according to Eq. (22) if λz = 0.99 is specified. As it is shown in Fig. 6,the shell generates a stable deformation if η < 0.32 (η = 0.28),and it will generate an unstable deformation if η > 0.32 (η = 0.32 and η = 0.36).
5 ConclusionsThe cylindrical shell,made of an incompressible EAP which is subjected to an internal pressure and a static electric field,may have an unstable non-monotonic deformation. There is a critical value for the internal pressure. When the internal pressure is larger than this value,the shell may have a complex non-monotonic deformation. The critical internal pressure increases with the increase of the axial stretch and the thickness,while it decreases with the increase of the voltage. There is also a critical value for the voltage. When the voltage is larger than this value,the shell produces a complex non-monotonic deformation. At the same time,there is a critical thickness for the wall of the shell. When the thickness is smaller than this critical thickness,the shell may have an unstable deformation.

|
| Fig. 6 Deformation curves for η = 0.28,η = 0.32,and η = 0.36 |
|
|
| [1] | Pelrine, R. E., Kornbluh, R. D., & Joseph, J. P. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sensors and Actuators A:Physical, 64, 77-85 (1998) |
| [2] | Pelrine, R. E., Kornbluh, R. D., Pei, Q., & Joseph, J. P. High speed electrically actuated elastomers with stretch greater than 100%. Science, 287, 836-839 (2000) |
| [3] | Heydt, R., Pelrine, R., Joseph, J., Eckerle, J., & Kornbluh, R. Acoustical performance of an electrostrictive polymer film loudspeaker. Journal of the Acoustical Society of America, 107, 833-839 (2000) |
| [4] | Dorfmann, L., & Ogden, R. W. Nonlinear response of an electroelastic spherical shell. International Journal of Engineering Science, 85, 163-174 (2014) |
| [5] | Plante, J. S., & Dubowsky, S. Large-scale failure modes of dielectric elastomer actuators. International Journal of Solids and Structures, 43, 7727-7751 (2006) |
| [6] | Zhao, X. H., Hong, W., & Suo, Z. G. Electromechanical coexistent states and hysteresis in dielectric elastomers. Physical Review B, 76, 134113 (2007) |
| [7] | Zhao, X. H., & Suo, Z. G. Method to analyze electromechanical stability of dielectric elastomers. Applied Physics Letters, 91, 061921 (2007) |
| [8] | Zhao, X. H., & Suo, Z. G. Theory of dielectric elastomers capable of giant deformation of actuation. Physics Review Letter, 104, 178302 (2010) |
| [9] | He, X. Z., Yong, H. D., & Zhou, Y. H. The response and stability of electro-active polymer cylindrical shells under the static and dynamic voltage. Chinese Journal of Solid Mechanics, 33, 341-347 (2012) |
| [10] | Yong, H. D., He, X. Z., & Zhou, Y. H. Electromechanical instability of anisotropic dielectric elastomers. International Journal of Engineering Science, 50, 144-150 (2012) |
| [11] | Li, T. F., Keplinger, C., Baumgartner, R., Bauer, S., Yang, W., & Suo, Z. G. Giant voltageinduced deformation in dielectric elastomers near the verge of snap-through instability. Journal of the Mechanics and Physics of Solids, 61, 611-628 (2013) |
| [12] | Lu, T. Q., An, L., Li, J. G., Yuan, C., & Wang, T. J. Electro-mechanical coupling bifurcation and bulging propagation in a cylindrical dielectric elastomer tube. Journal of the Mechanics and Physics of Solids, 85, 160-175 (2015) |
| [13] | Liu, Y. J., Liu, L. W., Sun, S. H., Zhang, Z., & Leng, J. S. Stability analysis of dielectric elastomer film actuator. Science in China Series E:Technological Sciences, 52, 2715-2723 (2009) |
| [14] | Díaz-Calleja, R., Riande, E., & Sanchis, M. J. On electromechanical stability of dielectric elastomers. Applied Physics Letters, 93, 101902 (2008) |
| [15] | Rudykh, S., Bhattacharya, K., & de Botton, G. Snap-through actuation of thick-wall electroactive balloons. International Journal of Non-Linear Mechanics, 47, 206-209 (2012) |
 2016, Vol. 37
2016, Vol. 37














