Shanghai University
Article Information
- YANG Tiemei, YANG Weiyang, LI Junlin, ZHANG Xuexia
- Analysis on non-oscillatory singularity behaviors of mode Π interface crack tip in orthotropic bimaterial
- Applied Mathematics and Mechanics (English Edition), 2016, 37(9): 1177-1192.
- http://dx.doi.org/10.1007/s10483-016-2123-6
Article History
- Received Nov. 11, 2015
- Revised Apr. 1, 2016
The singularity behaviors near the interface crack tip for isotropic, orthotropic, or anisotropic bimaterial have been widely studied[1-28].
If the stress singularity exponent is a complex number, the stresses near the interface crack tip will show oscillatory singularity behaviors. The oscillatory singularity behaviors have been widely investigated by analytical methods, e.g., the complex function method, the eigenfunction expansion method, the stress function method, the weight function method, and the integral transformation method, numerical methods, e.g., the finite element method and the boundary element method, and experimental methods[1-12, 26-28]. The oscillatory character of the stress and interface overlapping of the displacement cannot give ideal interpretation in the physical sense. If the stress singularity exponent is a real number, then the stresses near the interface crack tip will show non-oscillatory singularity behaviors[16-23]. Zhou and Wang[19] obtained the displacement functions by the governing equation containing four undetermined functions by the Schmidt method. Li et al.[20] and Yang et al.[22] obtained the stress functions by the governing equations containing sixteen undetermined coefficients and two stress singularity exponents with the stress function method and the method of elimination unknowns, respectively. Zhang et al.[23] obtained the stress functions by the governing equations containing eight undetermined coefficients and a stress singularity exponents with the method of elimination unknowns. However, since the stress singularity exponent is one or two real numbers[16-23], the stress oscillation and the interface overlapping of displacement never occur. Both the oscillatory and non-oscillatory singularity behaviors are considered in Refs.[13], [14], [15], [24], and [25].
In this paper, the non-oscillatory singularity behaviors of the mode II interface crack subjected to the loading at infinity, i.e., $| y| \to + \infty$ for orthotropic bimaterial, are investigated. The new stress functions are structured to be with eight or ten undetermined coefficients and an unknown singularity exponent. The characteristic equation and the stress singularity exponent are derived by the existence theorem of the non-trival solution for the system of eight homogeneous linear equations. Solving the system of twelve non-homogeneous linear equations with ten unknowns and using the uniqueness of the solutions for this equation system, we can obtain the ten undermined coefficients. The theoretical formulae of the stress intensity factors and the analytic solutions of the stresses near the mode II interface crack tip are obtained.
2 Complex function method and undetermined coefficient methodSuppose that the part when $y>0$ is occupied by the upper orthotropic material $(j=1)$, the part when $y<0$ is occupied by the lower orthotropic material $(j=2)$, the parts when $y=0$ and $| x| < a$ are the crack surfaces, and the part when $y=0$ and $| x |> a$ is the bonded interface of two dissimilar materials with a central crack of the length $2a$. The elastic constants and the compliance coefficients of each orthotropic material $j\;(j=1, \, 2)$ are $(E_1 )_j $, $(E_2 )_j$, $(\nu _{12} )_j$, $(G_{12} )_j$ and $(b_{11} )_j$, $(b_{22} )_j$, $(b_{12} )_j$, $(b_{66} )_j$, respectively. The relationships of these quantities are given by
With the compatibility equation for a linear elastic plane of the orthotropic bimaterial, we can deduce the governing equation as follows[29-33]:
where $ j=1, \, 2$, $x$ and $y$ are the Cartesian coordinates, and $U_j = U_j (x, y)$ is the stress function.
The fracture behaviors near the mode II interface crack tip for orthotropic bimaterial are discussed in this paper. The stress functions $U_j = U_j (x, y)\; (j = 1, 2)$ for this problem satisfy the governing equation (2) and the following boundary conditions:
We solve the partial differential equation (2) by a complex function method. Let
Then, substituting (6) into (2) yields the following biquadratic equations:
whose discriminants are
For two different orthotropic materials $j=1$ and $j=2$, there exist three cases: (i) $\Delta _1>0$ and $\Delta _2>0$, (ii) $\Delta _1<0$ and $\Delta _2<0$, and (iii) $\Delta _1>0$ and $\Delta _2<0$. In this paper, only Case (i) will be considered. Similarly, we can also discuss Cases (ii) and (iii).
When $\Delta _j>0$, we can obtain the characteristic roots of Eq.(2) as follows:
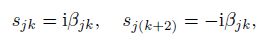 (9a)
(9a) 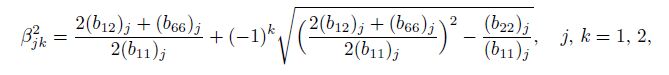 (9b)
(9b) where $\beta _{j2} > \beta _{j1} > 0.$
From Eqs.(7), (9), and (1), we have
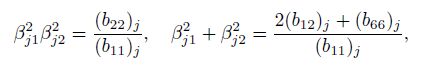 (10a)
(10a) 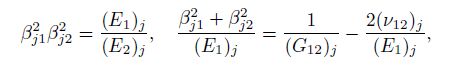 (10b)
(10b) where $j=1, \, 2.$ Introduce the following complex variables:
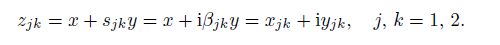 (11)
(11) Then, we have
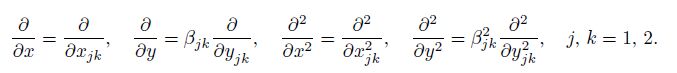 (12)
(12) From Eqs.(10a) and (12), we can reduce Eq.(2) to the generalized biharmonic equations as follows[29, 32-33]:
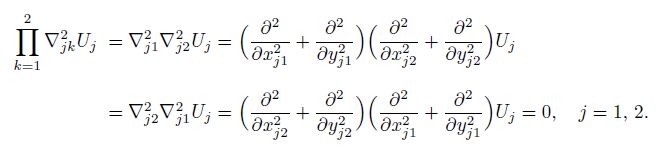 (13)
(13) By use of the undermined coefficient method, we can solve the fracture problem of the mode II interface crack tip in orthotropic bimaterial. The key lies in the determinations of the stress singularity exponent, the stress intensity factors, and the stresses.
The real part and the imaginary part of the analytic function of the complex variable $z_{jk}$ are both harmonic functions[34] and the solutions of Eq.(13), i.e., Eq.(2).
The stress singularity exponent of the mode II interface crack tip in the orthotropic bimaterial depends on the eight bimaterial self boundary conditions (3) and (4). It is not related to Eq.(5). Therefore, the special stress functions can be chosen as follows:
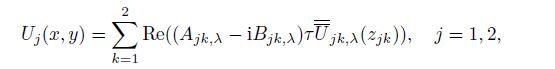 (14)
(14) where $A_{jk, \lambda }$ and $B_{jk, \lambda }\; (j, k = 1, 2)$ are eight undetermined coefficients. $\lambda$ is the stress singularity exponent, which sometimes is called eigenvalue. $z_{jk} \;(j, k = 1, 2)$ are given in Eq.(11). $\overline{\overline U} _{jk, \lambda } (z_{jk} )\;(j, k = 1, 2)$ are the analytic functions, and
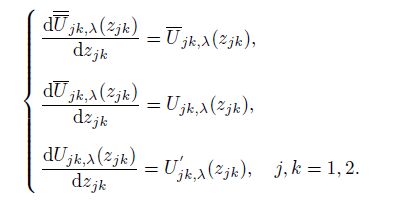 (15)
(15) Because Eq.(5) holds, the forward two conditions of Eq.(4) hold. Therefore, the boundary conditions (3), (4), and (5) have actually ten conditions. According to the similar reasons with Eq.(14), the solutions of the fracture problems (2), (3), (4), and (5) can be structured as follows:
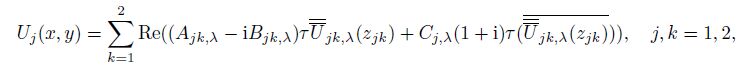 (16)
(16) where $A_{jk, \lambda }$, $B_{jk, \lambda }$, and $C_{j, \lambda }$ are ten undetermined coefficients. $\lambda$ is the stress singularity exponent. $z_{jk}\; (j, k = 1, 2)$ are given by Eq.(11). $\overline{\overline U} _{jk, \lambda } (z_{jk} )\;(j, k = 1, 2)$ are the analytic functions. $(\overline {\overline{\overline U} _{jk, \lambda } (z_{jk} )} )\;(j, k = 1, 2)$ denote the conjugate functions of $\overline{\overline U} _{jk, \lambda } (z_{jk} )\;(j, k = 1, 2)$.
3 Stress singularity exponent and existence of non-trivial solutionFrom Eqs.(14), (15), and(12), we can deduce the stresses of each material $j$$(j=1, \, 2)$ as follows[29-33]:
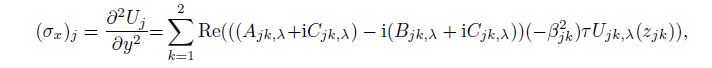 (17a)
(17a) 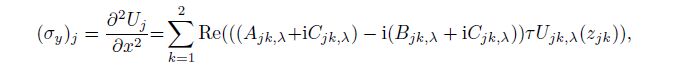 (17b)
(17b) 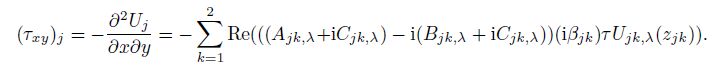 (17c)
(17c) Considering the boundary conditions (3) and (4), we choose $U_{jk, \lambda } (z_{jk} )$ of the right-side of Eq.(17) as follows:
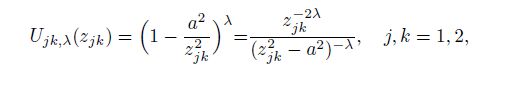 (18)
(18) where
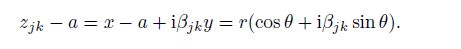 (19)
(19) In the above equation, $r$ and $\theta$ are the polar coordinates measured from the interface crack tip, and $z_{jk} \;(j, k = 1, 2)$ are expressed by Eq.(11).
From $- 1 = {\rm e}^{{\rm i}( - 1)^{j - 1} \pi} $, we know
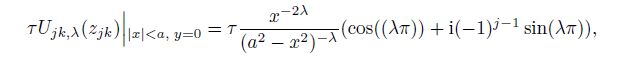 (20a)
(20a) 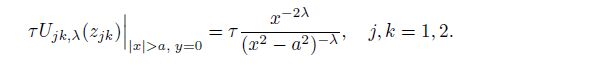 (20b)
(20b) Substituting Eqs.(20), (17b), and (17c) into Eqs.(3) and (4), after some calculations, we can obtain the eight equations as follows:
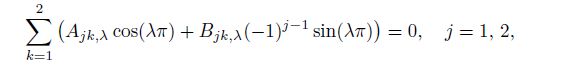 (21a)
(21a) 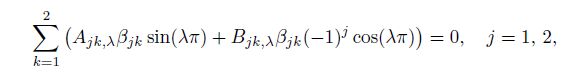 (21b)
(21b) 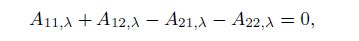 (22a)
(22a) 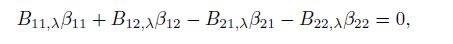 (22b)
(22b) 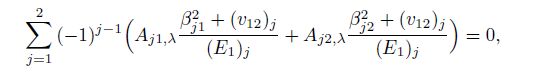 (22c)
(22c) 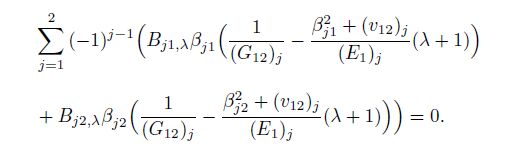 (22d)
(22d) We solve the system of the eight homogenous linear equations in Eqs.(21a)--(22d) by the successive elimination of the unknowns. The eight appropriate elementary transformations are made for the coefficient matrix $A_{8 \times 8}$ in Eqs.(21a)--(22d). Then, we can obtain the determinant as follows:
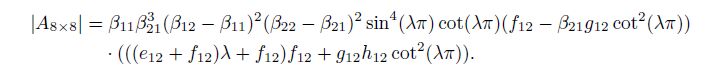 (23)
(23) The bimaterial parameters in Eq.(23) can be expressed by
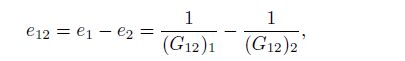 (24a)
(24a) 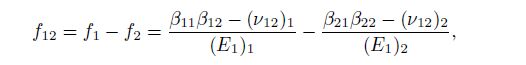 (24b)
(24b) 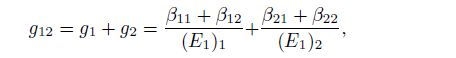 (24c)
(24c) 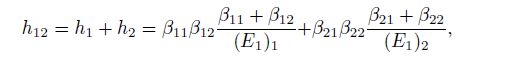 (24d)
(24d) where $e_j$, $f_j$, $g_j$, and $h_j$ are the parameters of each single material $j\;(j=1, \, 2)$.
By the existence theorem of the non-trivial solution for the equation system (21a)--(22d), from Eq.(23) and $| {A_{8 \times 8} } | = 0$, we can derive the characteristic equation of the mode II interface crack for the orthotropic bimaterial as follows:
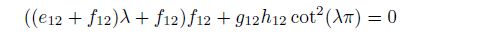 (25)
(25) or
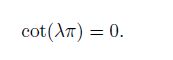 (26)
(26) Incidentally, from Eq.(23) and $| {A_{8 \times 8} } | = 0$, we have $\sin(\lambda\pi) = 0$, where $\lambda = n \;(n = 0, \, \pm 1, \, \pm 2, \, \cdots )$, in independent of $e_{12}$, $f_{12}$, $g_{12}$, and $h_{12}$, and they should be omitted.
Because the factor $\cot (\lambda\pi)$ can be included by Eq.(25), we can choose the stress singularity exponent as follows[16-24]:
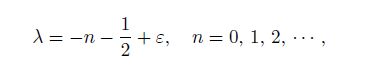 (27)
(27) where $\varepsilon$ is the positive real bielastic constant.
The fracture behavior at the crack tip for each material $j$ ($j=1, \, 2)$ directly affect the singularity state near the interface crack tip for the double materials, each of which is a single material. From the classical result for a single material, in the vicinity of the interface crack tip $(z_{jk} \to a, r \to 0) \;, n=0$ in Eq.(27), we have
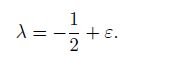 (28)
(28) Substituting Eq.(28) into Eq.(25), we obtain
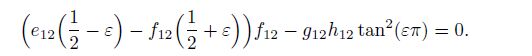 (29)
(29) Substituting the expansion of $\tan (\varepsilon \pi)$ in power series into Eq.(29), omitting the sufficiently small $\varepsilon$ at least the fourth degree, we can find the quadric characteristic equation as follows:
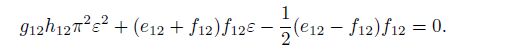 (30)
(30) When $e_{12} \ne 0$ and $f_{12} \ne 0$, in Eq.(24a) and (24b), the upper and lower materials are dissimilar. From Eq.(30), we can derive the following discrimination condition of the non-oscillatory singularity:
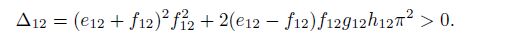 (31)
(31) If the parameters $e_{12}$, $f_{12}$, $g_{12}$, and $h_{12}$ satisfy the condition (31), then the bielastic constant $\varepsilon\; (\varepsilon > 0)$ can be determined by Eq.(30). Putting $\varepsilon$ into Eq.(28), we can obtain the real stress singularity exponent $\lambda$.
Solving Eq.(26), we can derive
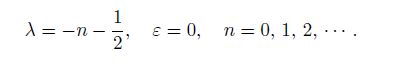 (32)
(32) By the same causes before Eq.(28), in the vicinity of the interface crack tip, we have $n=0$ in Eq.(32), and then
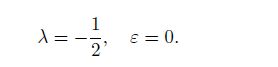 (33)
(33) The values of $\lambda$ in Eqs.(32) and (33) are independent of the bimaterial parameters in Eq.(24). Therefore, the stress singularity exponent of the orthotropic single material of the two orthotropic materials $j=1$ and $j=2$ are equal.
In fact, when the two orthotropic materials $j=1$ and $j=2$ are the same, the double materials will become a single material. Substituting $e_{12}=0$ and $f_{12}=0$ in Eq.(24) into Eq.(25), we can obtain the characteristic equation (26).
From the elastic constants in Refs.[23] and [36]--[38] and Eqs.(8) and (9), we can obtain the quantities $\Delta _j$ and $\beta _{jk} \;(j, k = 1, 2)$ of each orthotropic material (see Table 1). The mechanical parameters of each material in Table 1 are substituted into Eqs.(24), (28), (30), and (31). Then, we can obtain the bimaterial parameters, the discriminative conditions, the bielastic constant, and the real stress singularity exponent for the three orthotropic bimaterial (see Table 2).
Substituting Eq.(28) into Eq.(16), we can obtain the stress functions as follows:
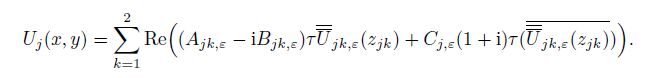 (34)
(34) From Eqs.(34), (15), (11), and (12), we can obtain $(\sigma _x )_j $, $(\sigma _y )_j$, and $(\tau _{xy} )_j$ of each material $j\;(j=1, \, 2)$ as follows[29-33]:
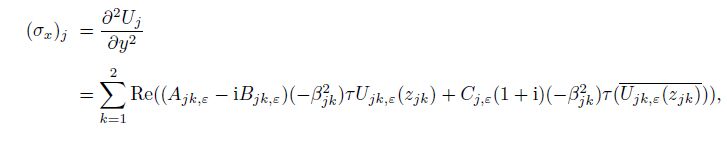 (35a)
(35a) 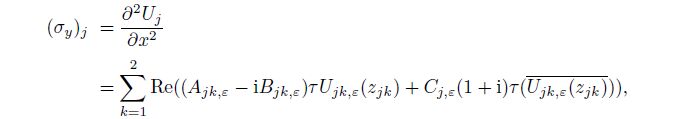 (35b)
(35b) 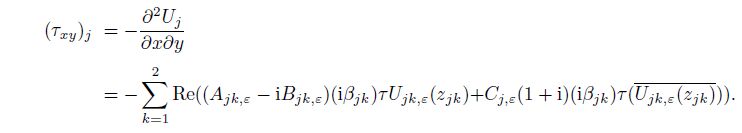 (35c)
(35c) Putting Eq.(28) into Eq.(18), we have
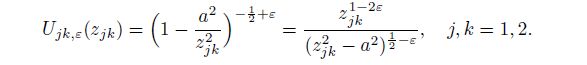 (36)
(36) From Eq.(36), Eq.(11), and $- 1 = {\rm e}^{{\rm i}( - 1)^{j - 1} \pi }$, we have
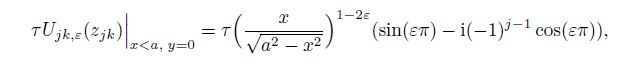 (37a)
(37a) 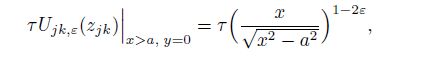 (37b)
(37b) 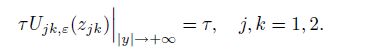 (37c)
(37c) Substituting Eqs.(37) and (35) into Eqs.(3), (4), and (5), and using the strain-stress relations and strain-displacement relations, we can derive the system of twelve non-homogeneous linear equations in ten unknowns as follows:
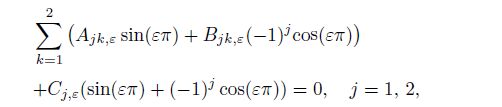 (38a)
(38a) 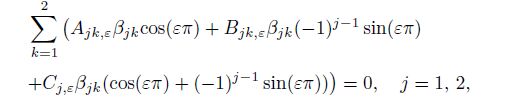 (38b)
(38b) 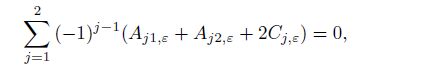 (39a)
(39a) 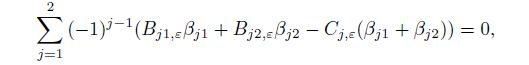 (39b)
(39b) 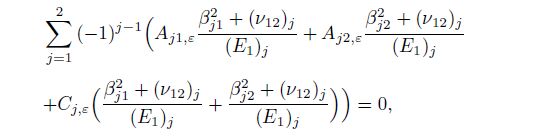 (39c)
(39c) 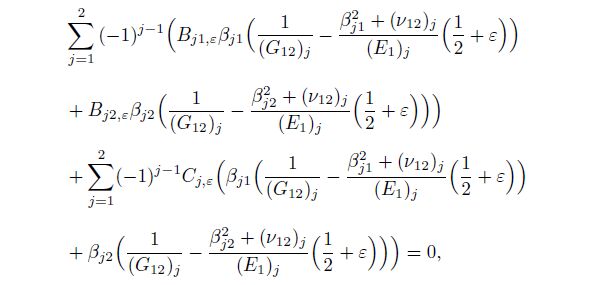 (39d)
(39d) 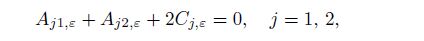 (40a)
(40a) 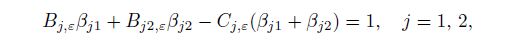 (40b)
(40b) where Eq.(40b) is non-homogeneous.
The coefficient matrix and the augmented matrix for the system of Eqs.(38a)--(40b) are denoted by $A_{12 \times 10}$ and $\overline{A}_{12 \times 11}=({A_{12\times 10} }$ $ b_{{\rm {II}}, 12\times1})$, respectively. Let $r_i$ and $c_j$ be the $i$th row and the $j$th column. To solve the system ${A_{12\times 10}X }=$ $ b_{{\rm {II}}, 12\times1}$ of Eqs.(38a)--(40b), we need to do the twelve elementary transformations for $\overline{A}_{12 \times 11}$. It is known that
where the number of the undetermined coefficients is 10. From this, the system of twelve non-homogeneous linear equations with the ten unknowns (38), (39) and (40) has and only has a unique solution[36], i.e., the ten undetermined coefficients are uniquely determined.
The augmented matrix for the system of the new ten nonzero rows is denoted by $\overline{A}_{10 \times 11} = (A_{10 \times 10} b_{{\rm {II}}, 10 \times 1} )$. The new system $A_{10 \times 10}X= b_{{\rm {II}}, 10 \times 1}$ of the non-homogeneous linear equations is solved by the inverse sequence back-substitution from down to up. The nine elementary transformations are taken for the new augmented matrix $\overline{A}_{10 \times 11}$. The expressions for the ten coefficients in the stress functions can be obtained as follows:
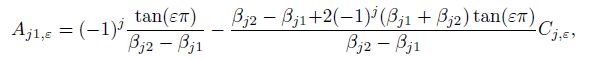 (41a)
(41a) 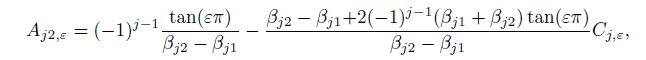 (41b)
(41b) 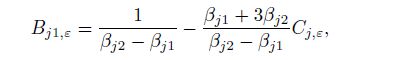 (41c)
(41c) 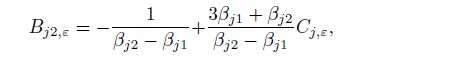 (41d)
(41d) 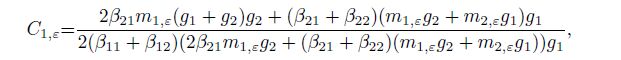 (41e)
(41e) 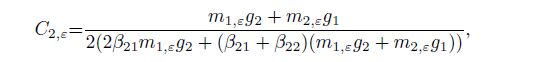 (41f)
(41f) where $j, k = 1, 2$, $\beta _{jk}$ are the imaginary parts of Eq.(9a) for Eq.(7), $e_j$, $f_j$, and $g_j$ are shown as Eq.(24), and
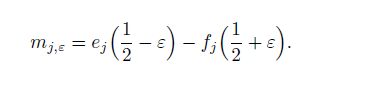 (42)
(42) The fracture problem of the mode II crack for the orthotropic single material can be reduced to solve the following boundary value problem:
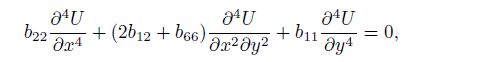 (43)
(43) 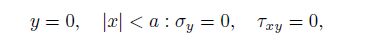 (44)
(44) 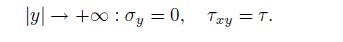 (45)
(45) Equation (43) can be converted into the generalized biharmonic equation[29, 32-33]. The boundary conditions (44) and (45) have four conditions. We can choose the stress function as follows:
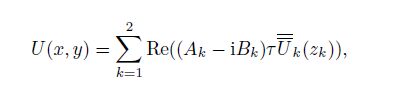 (46)
(46) where $A_k$ and $B_k$ are four undetermined coefficients, $\overline{\overline U} _k (z_k )$ are the analytic functions, and
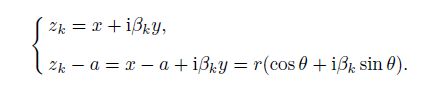 (47)
(47) From Eqs.(46) and (47), we can obtain the stresses as follows:
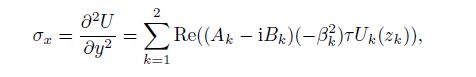 (48a)
(48a) 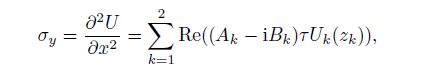 (48b)
(48b) 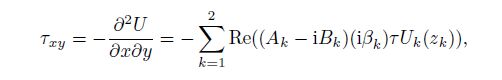 (48c)
(48c) where
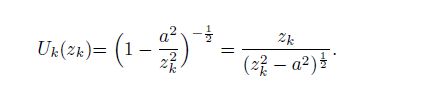 (49)
(49) From Eqs.(48) and (35), for the orthotropic single material, we have
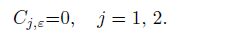 (50)
(50) We think that the single material is a special example of the double material. Putting $\varepsilon = 0$ in Eqs.(33) and (50) into Eq.(41), we have
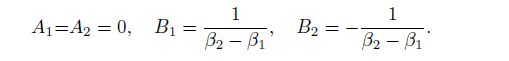 (51)
(51) Obviously, substituting Eqs.(49) and (48) into Eqs.(44) and (45), we can obtain the coefficient formulae (51).
5 Stress intensity factor and one-sided limitThe stress intensity factor depends on the stress, the stress function, the stress singularity exponent, and the applied outer load[5, 7, 9, 18]. Based on the stress expressions (35c) and (35b) and the one-sided limit, we can introduce the definitions on the stress intensity factors of the mode II interface crack in the orthotropic bimaterial for each material $j\;(j=1, \, 2)$ and the double material as follows:
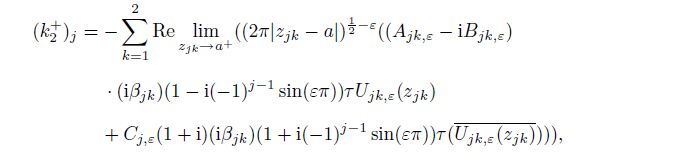 (52a)
(52a) 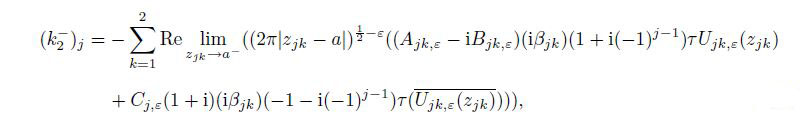 (52b)
(52b) 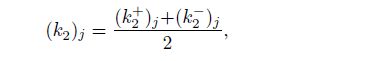 (52c)
(52c) 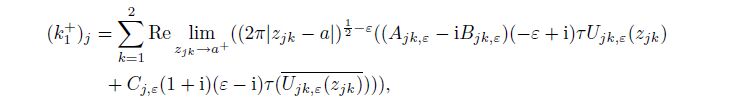 (53a)
(53a) 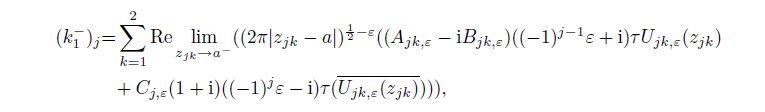 (53b)
(53b) 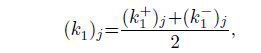 (53c)
(53c) where $j = 1, 2$, and
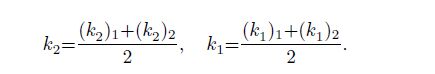 (54)
(54) By Eq.(19), we consider that $z_{jk} \to a^ +$ is the same as $r \to 0$ and $\theta \to ( - 1)^{j - 1} 0$, and $z_{jk} \to a^ -$ is the same as $r \to 0$ and $\theta \to ( - 1)^{j - 1} \pi$, where $j, k=1, 2$. From Eqs.(36) and (11), we have
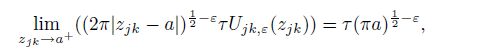 (55a)
(55a) 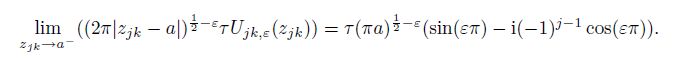 (55b)
(55b) 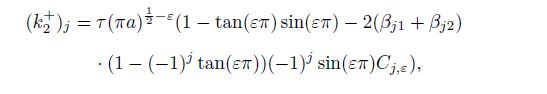 (56a)
(56a) 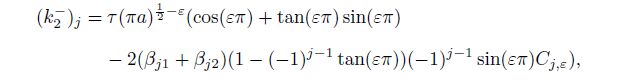 (56b)
(56b) 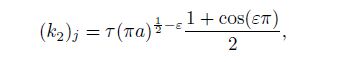 (56c)
(56c) 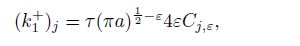 (57a)
(57a) 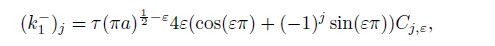 (57b)
(57b) 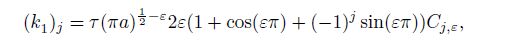 (57c)
(57c) 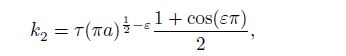 (58a)
(58a) 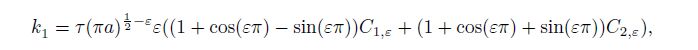 (58b)
(58b) where $C_{j, \varepsilon } \;(j = 1, 2)$ are given in Eqs.(41e) and (41f).
For the orthotropic single material, substituting $\varepsilon {\rm{ = }}0$ in Eq.(33) into Eq.(58), we can derive the stress intensity factor of the mode I crack as follows:
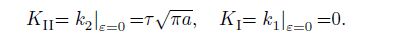 (59)
(59) With the data listed in Tables 1 and 2, From Eqs.(24) and (41e)--(42), we can obtain the related parameters of each orthotropic material (see Table 3).
From Eqs.(56c) and (57c), we can discover that the two one-sided limits create almost the same effects on the stress intensity factors of the materials $(k_2 )_j$ and $(k_1 )_j$ $(j=1, \, 2)$. Similarly, from Eq.(58), we can observe that the effects of the upper and lower materials on the stress intensity factors of the double material $k_2$ and $k_1$ are also nearly the same. These results occur because the coefficients (41) satisfy all the twelve boundary conditions in Eqs.(3), (4), and (5).
From Eqs.(58), (30), (41e), and (41f), we know that the variations of the normalized intensity factors $k_2 /\tau$ and $k_1 /\tau$ depend on the crack length $a$. The variations of the two factors for the mode II interface crack $k_2 /\tau$ and $k_1 /\tau$ with $a$ for the above three bimaterials are illustrated in Fig. 1. The minute variations of the factor $k_1 /\tau$ can be observed from the inner small figure of Fig. 1.

|
| Fig. 1 Normalized stress intensity factors of mode II interface crack as function of $a$ |
|
|
With Eq.(36), we have
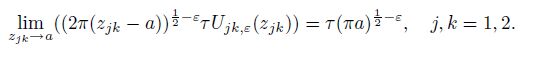 (60)
(60) With Eq.(60), we have
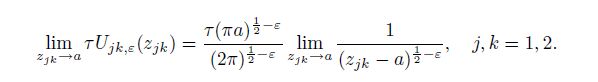 (61)
(61) Substituting Eqs.(41), (56c), (57c), (61), and (19) into Eq.(35), we can deduce the stresses in the vicinity of the mode II interface crack tip $(z_{jk} \to a, \;r \to 0, \;j, k = 1, 2)$ for the orthotropic bimaterial as follows:
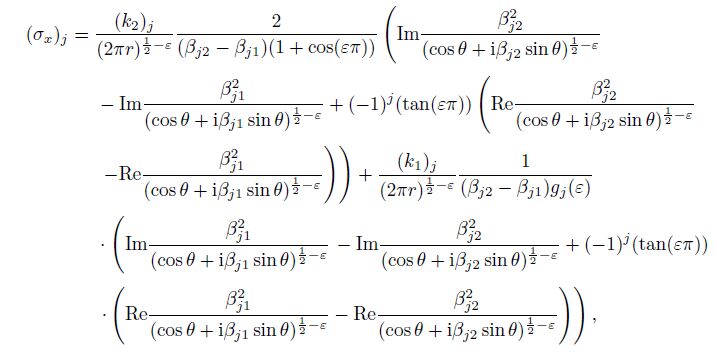 (62a)
(62a) 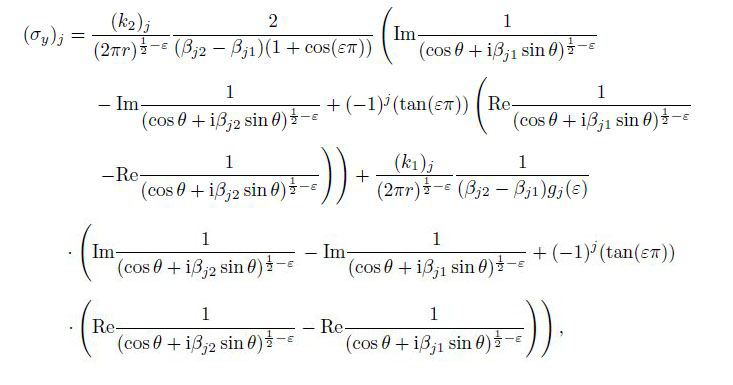 (62b)
(62b) 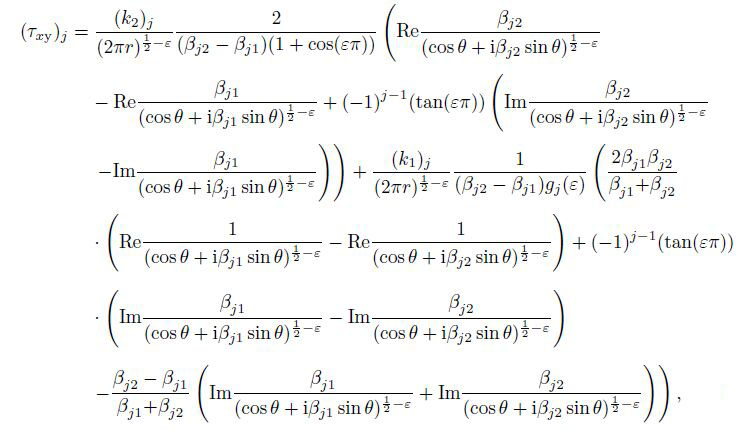 (62c)
(62c) where $j = 1, 2$, $0 < r \ll a, $ $j = 1: 0^ \circ < \theta < 180^ \circ$, $j = 2: -180^ \circ < \theta < 0^ \circ$, and $(k_2 )_j$ and $(k_1 )_j$ are the stress intensity factors of the orthotropic material $j$ shown in Eqs.(56c) and (57c), which can be rewritten as follows:
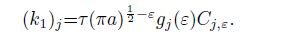 (63)
(63) Substituting Eqs.(56c), (63), and $\varepsilon {\rm{ = }}0$ in Eq.(33) into Eq.(62), considering Eqs.(50) and (59), we can obtain the analytic solutions of the stresses near the mode II crack tip $(z_{jk} \to a$, $r \to 0$, $j, k = 1, 2)$ for the orthotropic single material as follows:
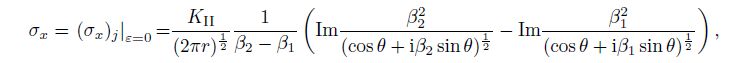 (64a)
(64a) 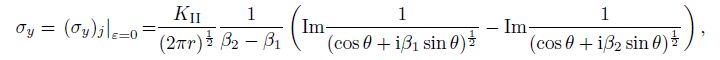 (64b)
(64b) 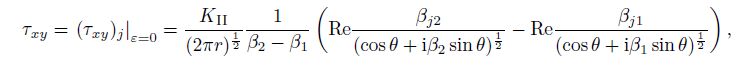 (64c)
(64c) where $0 < r \ll a$, and $- 180^ \circ < \theta <180^ \circ.$
The results of Eqs.(33), (59), and (64) agree well with the classical conclusions in Refs.[29]--[31]. This implies that the theoretical deductions are correct.
7 ConclusionsThe non-oscillatory singularity behaviors near the mode II interface crack tip for the orthotropic bimaterial are carefully studied. New special stress functions are constructed, containing ten undermined coefficients. The boundary conditions are transformed into the systems of eight homogeneous or twelve non-homogeneous linear equations. By the existence theorem of non-trivial solution for the system of the eight homogeneous linear equations, the characteristic equation and the stress singularity exponent of the orthotropic bimaterials are given, the discriminating condition of the non-oscillatory singularity is obtained. The uniqueness of the solution for the system of twelve non-homogeneous linear equations is proved, and the ten undermined coefficients in the stress function are uniquely determined. The stress intensity factors for the mode II interface crack are defined, and their theoretical formulae are derived. The analytic solutions of the stresses near the mode II interface crack tip for the orthotropic bimaterial are obtained. The results show that the stress intensity factors and the stresses possess mixed crack characteristics. The stress singularity exponent, the stress intensity factors, and the stresses of the mode II crack for the orthotropic single material are obtained. All of the results given in this paper have valuable significance in either academic researches or engineering applications.
| [1] | Williams, & M., L The stresses around a fault or crack in dissimilar media. Bulletin of the Seismological Society of America, 49, 199-204 (1959) |
| [2] | S, ih, & G., C Stress distribution near internal crack tips for longitudinal shear. Journal of Applied Mechanics, 32, 51-58 doi:10.1115/1.3625783 (1965) |
| [3] | England, & A., H A crack between dissimilar media. Journal of Applied Mechanics, 32, 400-402 doi:10.1115/1.3625813 (1965) |
| [4] | Erdogan, & F Stress distribution in bonded dissimilar materials with cracks. Journal of Applied Mechanics, 32(3), 403-410 (1965) |
| [5] | Ri, ce, J., R. and Sih, & G., C Plane problems of crack in dissimilar media. Journal of Applied Mechanics, 32, 418-423 doi:10.1115/1.3625816 (1965) |
| [6] | L, in, K., Y. and Mar, & J., W Finite element analysis of stress intensity factors for cracks at a bi-material interface. International Journal of Fracture, 12, 521-531 (1976) |
| [7] | S, un, C., T. and Jih, & C., J On stain energy release rates for interfactal cracks in bi-material media. Engineering Facture Mechanics, 28, 13-20 doi:10.1016/0013-7944(87)90115-9 (1987) |
| [8] | M, a, K., P. and Liu, & C., T Semi-weight function on computation of stress intensity factors in dissimilar materials. Applied Mathematics and Mechanics (English Edition), 25(11), 1241-1248 doi:10.1007/BF02438279 (2004) |
| [9] | Marsavina, L., and Sadowski, & T Stress intensity factors for an interface kinked crack in a bimaterial plate loaded normal to the interfaces. International Journal of Fracture, 145, 237-243 (2007) |
| [10] | Ch, en, Y, ., Qi, ao, P., Z., Jiang, H., D., and, Ren, & Q., W Review on experimental methods and fracture models for bi-material interfaces (in Chinese). Advances in Mechanics, 38, 53-61 (2008) |
| [11] | L, i, C, ., T, ie, Y, ., and, Zheng, & Y., P Influence of material characters on bimaterial interfacial crack energy release retes and stress intensity factors (in Chinese). Journal of Mechanical Engineering, 45, 104-108 doi:10.3901/JME.2009.03.104 (2009) |
| [12] | L, iu, Y., H., W, u, Z., G., Liang, Y., C., and, Liu, & X., M Numerical methods for determination of stress intensity factors of singular stress field. Engineering Fracture Mechanics, 75, 4793-4803 doi:10.1016/j.engfracmech.2008.06.007 (2008) |
| [13] | Chang, J., and Xu, & J., Q The singular stress field and stress intensity factors of a crack terminating at a bimaterial interface. International Journal of Mechanical Sciences, 49, 888-897 doi:10.1016/j.ijmecsci.2006.11.009 (2007) |
| [14] | D, ai, Y., and Ji, & X Researches on stress singulality of interface end and distributive law of interface stress (in Chinese). Science China, Physics, Mechanics & Astronomy, 37, 535-543 (2007) |
| [15] | Zhang, A., B. and Wang, & B., L An opportunistic analysis of the interface crack based on the modified interface dislocation method. International Journal of Solids and Structure, 50, 15-20 doi:10.1016/j.ijsolstr.2012.08.024 (2013) |
| [16] | Comininou, & M The interface crack. Journal of Applied Mechanics, 44, 631-637 doi:10.1115/1.3424148 (1977) |
| [17] | Dundurs, J., and Gautesen, & A., K An oppportunistic analysis of the interface crack. International Journal of Fracture, 36, 151-159 doi:10.1007/BF00017793 (1988) |
| [18] | Delale, F., and Erdogan, & F On the mechanical modeling of the interface region in bonded halfplane. Journal of Applied Mechanics, 55, 317-324 doi:10.1115/1.3173677 (1988) |
| [19] | Zh, ou, Z., G. and Wang, & B Investigation of the behavior of a Griffith crack at the interface between two dissimilar orthotropic elastic half-planes for the opening crack mode. Applied Mathematics and Mechanics (English Edition), 25(7), 730-740 (2004) |
| [20] | L, i, J., L., Zhang, S., Q., and, Yang, & W., Y Stress field near interface crack tip of double dissimilar orthotropic composite materials. Applied Mathematics and Mechanics (English Edition), 29(8), 1045-1051 (2008) |
| [21] | W, u, Z., G. and Liu, & Y., H Asymptotic fields near an interface corner in orthotropic bi-materials. International Journal of Fracture, 156, 37-51 doi:10.1007/s10704-009-9343-6 (2009) |
| [22] | Ya, ng, W., Y., Zhang, S., Q., L, i, J., L., and, Zhang, & X., X Interface crack problem for mode Π of double dissimilar orthotropic composite materials. Applied Mathematics and Mechanics (English Edition), 30(5), 585-594 (2009) |
| [23] | Zhang, X., X., C, ui, X., C., Ya, ng, W., Y., and, Li, & J., L Crack-tip field on mode Π interface crack of double dissimilar orthotropic composite materials. Applied Mathematics and Mechanics (English Edition), 30(12), 1489-1504 (2009) |
| [24] | Ya, ng, X., M., Ya, ng, W., Y., L, i, J., L., and, Zhang, & X., X Fracture analysis near the interface crack tip for mode I of orthotropic biomaterial. Science China Physics, Mechanics and Astronomy, 56, 785-797 doi:10.1007/s11433-013-5035-3 (2013) |
| [25] | S, uo, & Z Singularities, interfaces and cracks in dissimilar anisotropic media. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 427, 331-358 doi:10.1098/rspa.1990.0016 (1990) |
| [26] | Zhang, & X., S A central crack at the interface between two different orthotropic media for the mode I and mode Π. Engineering Fracture Mechanics, 32, 327-333 doi:10.1016/0013-7944(89)90304-4 (1989) |
| [27] | Erdogan, F., and Wu, & B., H Interface crack problems in layered orthotropic materials. Journal of the Mechanics and Physics of Solids, 41, 889-917 doi:10.1016/0022-5096(93)90004-Y (1993) |
| [28] | G, ao, H, ., Abbudi, M, ., and, Barnett, & D., M Interfacial crack-tip field in anisotropic elastic solids. Journal of the Mechanics and Physics of Solids, 40, 393-416 doi:10.1016/S0022-5096(05)80018-3 (1992) |
| [29] | Lekhnitskii, & S., G Theory of Elasticity of an Anisotropic Elastic Body (in Chinese). Science Press, Beijing, 1-33 (1963) |
| [30] | S, ih, G., C. and Liebowitz, & H Mathematical theories of brittle fracture. Mathematical Fundamentals of Fracture, Academic Press, New York, 89-131 (1971) |
| [31] | Corten, & H., T Fracture mechanics of composites. Fracture of Nonmetals and Composites, Academic Press, New York, 675-769 (1972) |
| [32] | S, ih, G., C. and Chen, & E., P Cracks in composite materials. Mechanics of Fracture, 7, 113-115 (1981) |
| [33] | Ya, ng, W., Y., L, i, J., L., and, Zhang, & X., X Method of a Complex Variable for Fracture in Composite Materials (in Chinese) (2005) |
| [34] | Ya, ng, W., Y. and Zhang, & S., Q The analysis about the stress field near model I crack tip in composite material (in Chinese). Journal of Taiyuan Heavy Mechinery Institute, 7, 46-53 (1986) |
| [35] | Y, u, & J., R Function of a Complex Variable (in Chinese) (1979) |
| [36] | R, en, & B., S Advanced Algebra (in Chinese) (2002) |
| [37] | Baldi, & A Full field methods and residual stress analysis in orthotropic material, Π:nonlinear approach. International Journal of Solids and Structures, 44, 8244-8258 doi:10.1016/j.ijsolstr.2007.06.002 (2007) |
| [38] | Zhang, S., Q. and Yang, & W., Y Prediction of mode I crack propagation direction in carbor-fiber reinforced composite plate. Applied Mathematics and Mechanics (English Edition), 25(6), 714-722 (2004) |
 2016, Vol. 37
2016, Vol. 37














