Shanghai University
Article Information
- HU Jun, HENRY D., BENHADID H., YIN Xieyuan
- Transient growth in Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect
- Applied Mathematics and Mechanics (English Edition), 2016, 37(9): 1203-1218.
- http://dx.doi.org/10.1007/s10483-016-2121-6
Article History
- Received Aug. 27, 2015
- Revised May. 7, 2016
2. Laboratoire de Mécanique des Fluides et d'Acoustique, CNRS/Universit éde Lyon, Ecole Centrale de Lyon/Université Lyon 1/INSA de Lyon, ECL, 36 avenue Guy de Collongue, 69134 Ecully Cedex, France;
3. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China
The mixed convection in binary mixtures with the Soret effecthas many practical applications,e.g.,chemical vapour deposition(CVD) in the electronic industry. It also leads to rich and complexspatiotemporal pattern formations,which have a great theoreticalinterest. In fact,the already rich spatiotemporal behavior of thedissipative structures occurring in binary mixtureconvection[1] may be affected by the externally imposedthrough-flow. It is why the Poiseuille-Rayleigh-Bénard flowshave been intensively studied for small Reynoldsnumbers[2-5] by linear,nonlinear,and transientbehaviors,dealing with either temporal or spatiotemporalinstabilities.
How a horizontal plane Poiseuille shear flow changes the linear convection properties in heated binary fluid layers was first investigated by Jung et al.[2]. They solved the full linear stability equations by a shooting method for realistic top and bottom boundary conditions,and found that the through-flow brokethe symmetrical left and right traveling waves (TW),and thefrequencies,bifurcation thresholds,and structural properties ofthe two symmetry degenerate TW solution branches as well as thestationary overturning convection (SOC) were changed dramatically.Later,Büchel and Lücke[3] studied the effect of a horizontal through-flow with small Reynolds numbers on stationary and traveling wave convective patterns with a Galerkin expansion anda finite difference numerical method. The bifurcation diagrams ofvarious quantities,e.g.,the Nusselt number,the frequency,and the mixing behavior,are determined as functions of the heating rate andthe wave number for several through-flow rates and the Soret coupling strengths for the ethanol-water parameters. They alsos tudied the growth dynamics of small convective perturbations into different and strongly nonlinear convective states and the transition between them.
Concerning the study of the absolute and convective instability,the boundary curves separating these two types of instabilities for both negative separation factors (corresponding to the two symmetry degenerate TW solutions) and positive separation factors (corresponding to the SOC solution) were first plotted as a function of the through-flow rate by Jung et al.[2]. Later,Büchel and Lücke[4] studied the spatiotemporal properties of the spatially localized convective perturbations in detail for heated binary fluid layers with or without a through-flow. The fronts and pulse-like wave packets formed out of the three relevant perturbations (two oscillatory perturbations and a stationary perturbation) were analyzed after evaluating the appropriate saddle points of the three respective dispersion relations of the linear stability equations over the complex wave number plane. Jung and Lücke[5] further compared the spatiotemporal properties of the fronts obtained from the saddle point analysis of the dispersion relation of the linear field equations with the numerical solutions of the full nonlinear hydrodynamical equations. Using the Chebyshev collocation method to solve the full linear stability equations,Hu et al.[6] investigated the temporal and spatiotemporal instabilities of the Poiseuille-Rayleigh-Bénard flows for much larger Reynolds numbers. For positive separation factors,they found that the critical thresholds strongly increased when the through-flow was used,and the boundary curves between the absolute instability (AI) and the convective instability (CI) increased as well,but more steeply. For enough large positive separation factors,there existed three local minima in the neutral curves Ra(k) (the Rayleigh number against the wavenumber) for moderate Reynolds numbers,resulting in the discontinuity of the critical wavenumber curve and the non-smoothness of the critical Rayleigh number curve when the Reynolds number varied. For negative separation factors,there existed a contact point between the critical Rayleigh number curve and the AI/CI boundary curve,at which the fluid system directly changed from stable to absolutely unstable without crossing the convectively unstable region. Through an energy budget analysis for the binary fluid system,it was found that,when the separation was positive (negative),the solutal buoyancy contribution would make the system unstable (stable).
It is well-known that the effect of the non-normality in plane Poiseuille,Couette,or other channel flows can enable large transient growth prior to eventual exponential decay[7-11]. For optimal disturbances for plane Poiseuille flows,the Orr-mechanism and lift-up mechanism have been revealed to be responsible for the two-dimensional and three-dimensional optimal disturbances,respectively. For optimal disturbances for the Poiseuille-Rayleigh-Bénard flows of pure fluids,it has also been found[12] that streamwise-uniform perturbations can produce large streamwise streaks and Rayleigh-Bénard convection rolls at moderately large Reynolds numbers for all Rayleigh numbers and Prandtl numbers. The transient growth of linearly stable disturbances is believed to play an important role in the subcritical transition of many flow systems,especially for shear flows. It has already been revealed that the Poiseuille-Rayleigh-Bénard flows are subcritically unstable for negative separation factors[3],while their non-normal transient growth has not been intensively studied. This constitutes the main content of this paper.
2 FormulationWe consider a non-reactive binary fluid mixture contained in an infinite horizontal channel of the height H (see Fig. 1). The binary mixture is heated as follows. The horizontal boundaries are isothermal and held at different temperatures. The temperature at the top wall (z=H) is T2,the temperature at the bottom wall (z=0) is T1,and T1 > T2. A through-flow in the x-direction is also driven by imposing a constant pressure gradient along the channel. The resulting global flow is usually called the Poiseuille-Rayleigh-Bénard flow. Due to the gravitational effect,the binary mixture may become unstable when the vertical temperature and concentration gradients exist. To take this into account,the Boussinesq approximation is used such that the density variations are restricted to the buoyancy term,and are expressed as a linear law,i.e.,

|
| Fig. 1 Schematic representation of Poiseuille-Rayleigh-Bénard model |
|
|
where βT and βC are the thermal and solutal expansion coefficients,respectively,p0,T0,and C0 are the reference values for the density,temperature,and concentration,respectively,which are taken as mean values.
The Soret effect,which arises as the contribution of the increase in the temperature gradient to the mass flux,is considered here,whereas the Dufour effect,which arises as the contribution of the increase in the concentration gradient to the heat flux,is neglected. The mass flux J C and the heat flux J Tare
where D C,DS,and DT are the solutal diffusion coefficient,the Soret diffusion coefficient,and the thermal conductivity,respectively. The conductive steady state will then correspond to the linear variations along the z-direction for both the temperature and the concentration,leading to a concentration difference
where ΔT = T1 − T2.
The flow in this system is modelled by the Navier-Stokes equations coupled to an energy equation and a concentration equation. In these equations,the length,velocity,time,and pressure are scaled by H,k/H,H2/k,and p0k2/H2,respectively,where k is the thermal diffusivity. The dimensionless temperature θ and concentration c are,respectively,defined by
Thus,the dimensionless governing equations of the three-dimensional Poiseuille-Rayleigh-Bénard flow are
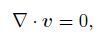 (3a)
(3a) 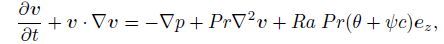 (3b)
(3b) 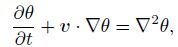 (3c)
(3c) 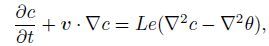 (3d)
(3d) where v=(u,v,w) is the three-dimensional dimensionless velocity vector,ez is the unit vector in the vertical direction,and the operators are
The dimensionless parameters appearing in Eq.(3) are the Prandtl number Pr,the Rayleigh number Ra,the separation factor ψ,and the Lewis number Le defined by
where v is the kinematic viscosity. The corresponding boundary conditions are
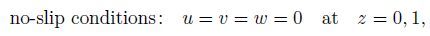 (4a)
(4a) 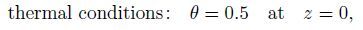 (4b)
(4b) 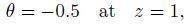 (4c)
(4c) 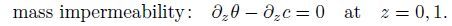 (4d)
(4d) The non-dimensional basic steady state can easily be obtained,and corresponds to a parabolic z-profile for the x-component of the velocity vector (throughflow),a constant pressure gradient responsible for this throughflow,and a vertical pressure gradient to balance the vertical density variations and to linearize the conductive z-profiles for the temperature and concentration,i.e.,
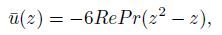 (5a)
(5a) 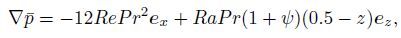 (5b)
(5b) 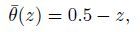 (5c)
(5c) 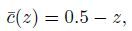 (5d)
(5d) where Re=U0H/v is the Reynolds number,and U0 is the dimensional mean velocity obtained by integration over the channel height.
The disturbed three-dimensional Poiseuille-Rayleigh-Bénard flow with the Soret effect can be decomposed as follows:
Then,the perturbations u′,v′,w′,p′, θ′,and c′ are the solutions of the following equations:
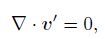 (6a)
(6a) 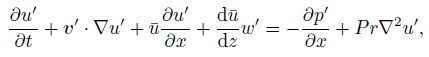 (6b)
(6b) 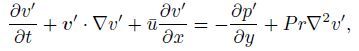 (6c)
(6c) 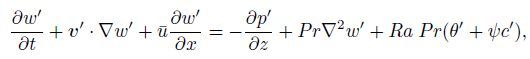 (6d)
(6d) 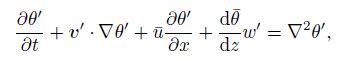 (6e)
(6e) 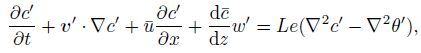 (6f)
(6f) where v′=(u′,v′,w′). Furthermore,by neglecting the quadratic term with respect to small disturbance,we can obtain the following linearized perturbation equations:
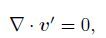 (7a)
(7a) 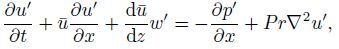 (7b)
(7b) 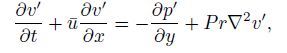 (7c)
(7c) 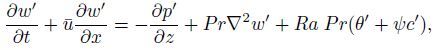 (7d)
(7d) 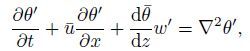 (7e)
(7e) 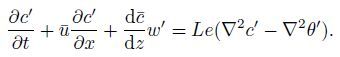 (7f)
(7f) The corresponding boundary conditions are
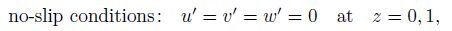 (8a)
(8a) 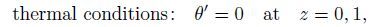 (8b)
(8b) 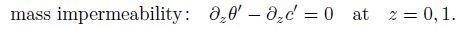 (8c)
(8c) Taking the divergence of the linearized momentum equations (7b),(7c),and (7d) and using Eq.(7a) yield an equation for the pressure perturbation as follows:
This equation may be used with Eq.(7d) to eliminate p′,resulting in an equation for the normal velocity as follows:
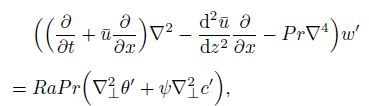 (10)
(10) where
To describe the complete three-dimensional flow field,an additional equation is needed. The most convenient way is to write the equation for the vorticity perturbation along z,i.e.,
Then,we can obtain
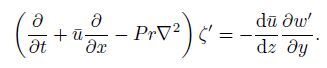 (11)
(11) Thus,the linearized perturbation equations can be written as follows:
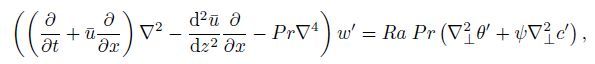 (12a)
(12a) 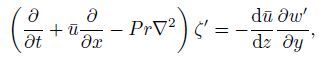 (12b)
(12b) 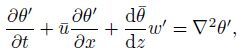 (12c)
(12c) 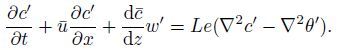 (12d)
(12d) These equations associated with the boundary conditions
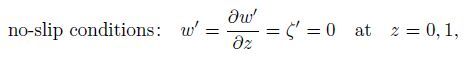 (13a)
(13a) 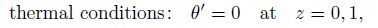 (13b)
(13b) 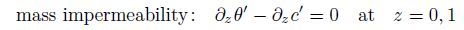 (13c)
(13c) and the initial conditions
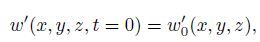 (14a)
(14a) 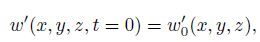 (14b)
(14b) 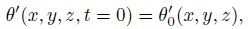 (14c)
(14c) 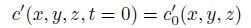 (14d)
(14d) provide a complete description for the evolution of an arbitrary small disturbance in both space and time.
The perturbation quantities can further be expanded as exponential functions of time and the following streamwise and spanwise coordinates:
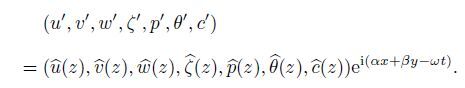 (15)
(15) From Eqs.(12a)--(13c),we can see that 



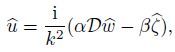 (16a)
(16a) 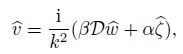 (16b)
(16b) 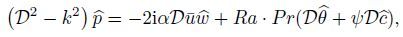 (16c)
(16c) where
After substituting Eq.(15) into Eqs.(12a)--(13c),the independent eigenfunctions can be obtained by solving the following eigenvalue problem:
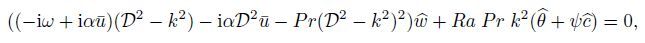 (17a)
(17a) 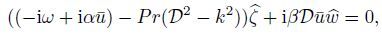 (17b)
(17b) 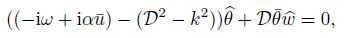 (17c)
(17c) 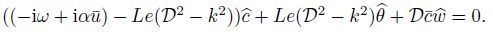 (17d)
(17d) Introduce
Then,the above linear stability equations can be rewritten as follows:
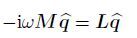 (18)
(18) with the boundary conditions
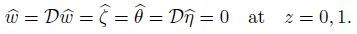 (19)
(19) The expressions of the matrices are
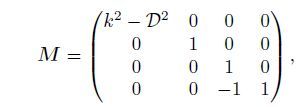 (20)
(20) 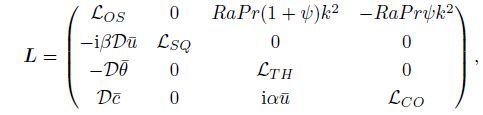 (21)
(21) 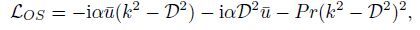 (22)
(22) 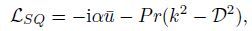 (23)
(23) 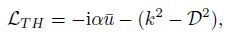 (24)
(24) 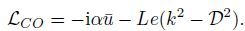 (25)
(25) Equation (17a)--(17d) are ordinary differential equations
in terms of 

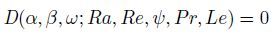 (26)
(26) should be satisfied. We need to solve an eigenvalue problem. Because it is impossible to find the explicit analytical dispersion relation if there is no further simplification,the dispersion relation has to be obtained numerically. A shooting method has been adopted for this problem in the paper of Jung et al.[2]. In this paper,the pseudospectral Chebyshev method[13] is used to discretize the eigenvalue problem,and the QZ algorithm is used to solve the resulting general eigenvalue problem.
In order to study the transient growth of the Poiseuille-Rayleigh-Bénard flows for binary fluids,we need to derive a physically meaningful way to measure the size of the perturbation. Thus,we define a modified kinetic energy of the perturbation by
 (27)
(27) where the superscript H indicates the conjugate transpose. The involved matrix is a positive defined weight matrix,so that a norm and inner product can be defined by
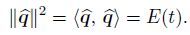 (28)
(28) The initial linearized problem (12) can also be written as follows:
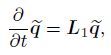 (29)
(29) where
The solution qn can be expressed as follows:
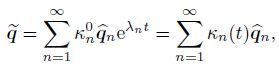 (30)
(30) where 
The approximated solution q is obtained from the truncation of the exact series solution (30). Then,we can write
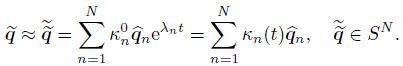 (31)
(31) If we define
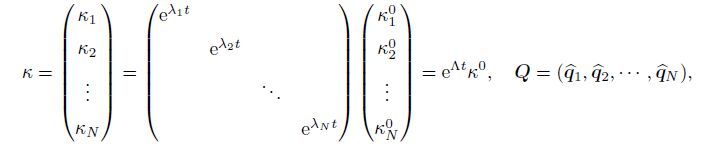 (32)
(32) then
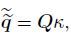 (33)
(33) and
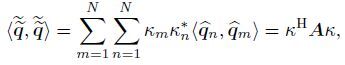 (34)
(34) where A,in which Anm=
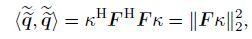 (35)
(35) where ||.||2 is the L2-norm (sum of squares). From Eq.(28),we can approximate the energy of the perturbation as follows:
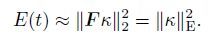 (36)
(36) We want to estimate the growth of a perturbation initially given by k^0 as a function of time. We define the energy amplification factor g(t) as the ratio between the energy of the perturbation at the time t and its initial energy,i.e.,
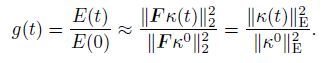 (37)
(37) For a fixed time t,we want to maximize g(t) over the set of all possible initial conditions k0. This maximization leads to the optimal energy amplification factor G(t) as follows:
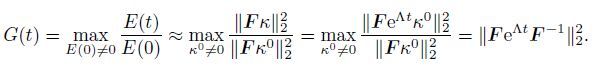 (38)
(38) The quantity G(t) gives the maximum amplification optimized over all possible initial conditions. In general,each point on the curve G(t) is arrived at by an independent initial condition,and G(t) represents the envelope of the individual growth curves. For the computation of G(t),the key step is to use a singular value decomposition of the matrix A to obtain the matrix F,and then a singular value decomposition of the matrix F eΛt F-1 is performed at each chosen time t. The concrete arithmetic for the plane Poiseuille flow can be found in Ref.[11].
3 Numerical resultsWe first consider the transient growth for the negative separation factor ψ=-0.1 and the small Reynolds number Re=0.15 (see Fig. 2),which shows the optimal energy amplification factor G(t) for the optimal disturbances to the linearly stable and unstable Poiseuille-Rayleigh-Bénard flows with the stream-wise wave number α=3.14 and β=0.

|
| Fig. 2 Optimal energy amplification factor G(t) as function of time t for Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect and Ra=1800 (linearly stable),1950 (linearly unstable),where α=3.14,β=0.0,ψ=-0.1, Re=0.15,Pr=10,and Le=0.01 |
|
|
From Fig. 2,we can see that the initial transient growth can achieve a large amplification with the order 102~103. The maximum amplification occurring at t≈ 0.233 can be obtained only by the two least-stable modes (N=2),i.e.,the upstream and downstream modes,and it has little change when the number of the least-stable modes increases from N=2 to N=4,8. After the initial transient growth,a global cycle appears with a period T,and finally exponentially damps or amplifies for the linearly stable or unstable flow due to the dominated effect of the least-stable mode. Interestingly,it is found that the cycle period is connected to the angular frequency difference of the upstream and downstream modes with T ≈ 2 π / |w1r -w2r|. For Ra=1800,the angular frequencies of the upstream and downstream modes are w1r = -0.10294646,and w2r = 12.61900485,and the period T is about 0.494,agreeing with Fig. 2(a). While for Ra=1950,the angular frequencies are w1r = -0.35549672,and w2r = 12.85576413,and the period T is about 0.4756,agreeing with Fig. 2(b). It is thus verified that the global periodic cycle of the optimal energy amplification is only determined by the non-normal interaction of the upstream and downstream modes. The addition of the least-stable modes affects the optimal growth only slightly for long time.
For the positive separation factor ψ=0.1 with the same Reynolds number and stream-wise wave number,we plot Fig. 3 to present the optimal energy amplification factor G(t) for the optimal disturbances to the linearly stable and unstable flows. It is easily found that the initial transient growth achieves only when the maximum amplification of the order O(1) is near t=1,which is far smaller than that for the negative separation factor ψ=-0.1. In addition,it is clearly seen that the least-stable mode will govern the exponential behavior of the optimal growth function for long time (t >2) without the existence of the periodic cycle like ψ=-0.1. Furthermore,with the increase in the number in the least-stable modes to plot the optimal energy amplification,the characteristics of the transient growth change significantly,and obviously,the optimal energy amplification for N=14 is nearly three times larger than that for N=9.

|
| Fig. 3 Optimal energy amplification factor G(t) as function of time t for Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect and Ra=300 (linearly stable),350 (linearly unstable),where α=3.14,β=0.0,ψ=0.1, Re=0.15,Pr=10,and Le=0.01 |
|
|
Let us now further examine the maximum growth function Gmax=maxt G(t) in the αβ-plane for Poiseuille-Rayleigh-Bénard flows of binary fluids with the Soret effect (see Fig. 4). It is found that,for the negative separation factor ψ=-0.1 and the Rayleigh number Ra=1800 shown in Fig. 4(a),the distributions of the maximum growth function are like concentric circles,while the optimum of Gmax is about 885. This growth is achieved for α=0.0 and β≈ 4.0.In addition,we find that it occurs at the time t≈ 0.174. For the positive separation factor ψ=0.1 and the Rayleigh number Ra=300 shown in to the squire transformation for the least-stable OS mode,there exists a large unstable eigenvalue region in the αβ-plane,where Gmax==∞ for t→∞. It is bounded by the bold solid neutral curve shown in Fig. 4(b). The optimum of Gmax is near the contour line Gmax=11,and exactly occurs at the neutral curve. For the pure stream-wise disturbance,it is found that the optimum of Gmax is located at α≈ 5.4.

|
| Fig. 4 Contours of maximum transient growth Gmax in αβ-plane for Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect and negative separation factor (ψ=-0.1,Ra=1800) or positive separation factor (ψ=0.1,Ra=300),where Re=0.15,Pr=10,and Le=0.01 (N=31 least-stable spectra are used) |
|
|
So far,only a small Reynolds number Re=0.15 has been investigated for the optimal transient growth of the Poiseuille-Rayleigh-Bénard flows. It is necessary to study the Reynolds number dependence of the optimal transient growth with pure streamwise disturbance for the negative separation factor ψ=-0.1 (Ra=1800) and positive separation factor ψ=0.1 (Ra=300) (see Fig. 5). Figure 5(a) shows that,for the stream-wise disturbances with long or moderate wavelength (α <3),the Reynolds number effect on the optimal transient growth is very weak,while for large stream-wise wave numbers (α >3),with the increase in the Reynolds number,the maximum growth function decreases,showing that the inertial effect has a stabilized effect on the transient growth. Furthermore,it is clearly seen that the stabilizing role of the inertia is the most significant for the wavenumber α≈ 4.0. Thus,the optimum of Gmax occurs at Re=0 and α≈ 4.0. In Fig. 5(b),there exists an unstable region for small Reynolds numbers,beyond which the characteristics of the transient growth are similar to those in Fig. 5(a),i.e.,with the increase in the Reynolds number,the maximum growth function decreases. This stabilization effect also occurs at much larger wave number region.

|
| Fig. 5 Contours of maximum transient growth G max in α Re-plane for Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect and negative separation factor (ψ=-0.1,Ra=1800) or positive separation factor (ψ=0.1,Ra=300),where β=0.0,Pr=10,and Le=0.01 (N=31 least-stable spectra are used) |
|
|
As mentioned above,for the stream-wise disturbance with α=3.14,the variation of small Reynolds numbers has a slight effect on the maximum transient growth. Therefore,under this situation,it is convenient to study the combined effects of the separation factor and Rayleigh number on the optimal transient growth with the small Reynolds number Re=0.15. For this purpose,the contours of the maximum transient growth Gmax= are plotted in Fig. 6 for both negative and positive separation factors. Figure 6(a) shows an unstable region on the upper right corner,beyond which the maximum growth function increases to the order O(103) with the increase in the Rayleigh number and the decrease in the separation factor. This reveals an important fact that small negative separation factors can make very large transient amplification though the flow system needs a large Rayleigh number to become linearly unstable. From Fig. 6(b),it is found that the contour curve of the maximum transient growth is parallel to the ψ-Ra neutral curve,and the increases in the Rayleigh number and the positive separation factor can produce larger transient amplification with the order O(1).

|
| Fig. 6 Contours of maximum transient growth G max in ψ Ra-plane for Poiseuille-Rayleigh-Bénard flows of binary fluids with Soret effect and negative or positive separation factor, where α=3.14,β=0.0,Re=0.15,Pr=10,and Le=0.01 (N=31 least-stable spectra are used) |
|
|
Similar to our usual understanding of the perturbation pattern at the critical points of the flow instability onset,it is also instructive and interesting to exhibit the pattern of the initial disturbance that gives the largest amplification for a given time. From the definition (38) of the optimal energy amplification factor, a singular value decomposition (SVD) should be performed,i.e.,
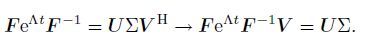 (39)
(39) Obviously,the largest singular value is just the square root of G(t),and the the singular vectors in V and U associated with the largest singular value are,respectively,the desired optimal initial condition and the maximum amplified spatial pattern at a given time. Usually,the singular values are ordered in a decreasing manner. Therefore,the first columns of V and U are our desired singular vectors,and we denote them as v_1 and U,respectively. Then,the optimal initial condition can be obtained from
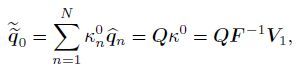 (40)
(40) and the spatial pattern at the given time t spec evolved from the above initial optimal disturbance can be obtained by
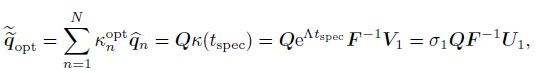 (41)
(41) where σ1 is the largest(principal) singular value.
As we have already known,a large transient growth can be obtained by the two-dimensional pure optimal stream-wise disturbance for the negative separation factor ψ=-0.1 (see Fig. 2(a)). The maximum optimal amplification occurs at tmax≈ 0.233. Thus,we can perform the singular value decomposition of FeΛtmaxF-1 to get v_1 and U1 for this maximum optimal amplification. Then,from Eqs.(40) and (41),we can obtain the optimal initial and evolutionary spatial patterns,whose velocity vector (u,w), spanwise vorticity ξ,temperature θ,and concentration c fields are plotted in Fig. 7.

|
| Fig. 7 Spatial patterns for initial optimal disturbance (left column) and maximum optimal amplification at t max}≈ 0.233 (right columns) for velocity vector (u,w) (see (a) and (b)),spanwise vorticity $\xi$ (see (c) and (d)),temperature θ (see (e) and (f)),and concentration c fields (see (g) and (h)),where α=3.14,β=0.0,ψ=-0.1, Ra=1800,Re=0.15,Pr=10,and Le=0.01 (N=31 least-stable spectra are used) |
|
|
It is clearly seen from these two subfigures that the spanwise vorticity achieves a large amplification with the order O(10^2). Moreover,it is found that the largest spanwise vorticities occur near the upper and lower rigid walls.
Furthermore,for the temperature and concentration fields shown in Figs. 7(e),7(f),7(g),and 7(h),after the transient growth from the optimal disturbance,the amplitude of the temperature field magnifies three times and that of the concentration field decreases to one-eighth of the initial amplitude. It is also seen that the contour of the concentration field has a complex distort shape at the time of the maximum optimal amplification.
4 ConclusionsIn this paper,a large transient growth with the order O(102) is revealed for the Poiseuille-Rayleigh-Bénard flows of binary fluids with the Soret effect for negative separation factors due to the subcritical unstable characteristic. It is interesting that this large transient growth can be produced only by the two least-stable modes for small Reynolds numbers. Large Reynolds numbers even have an obvious stabilization effect on the transient growth for moderate wave numbers. Thus,the negative separation factor and the Rayleigh number play a key role for the large amplification of energy norm.
The spatial patterns of the optimal disturbances for the large transient growth are plotted for two-dimensional pure streamwise disturbances. For the velocity vector field,the initial three-layer cell vorticity structure is found and developed into one cell at the time t max when the maximum optimal amplification with the order O(102) is obtained.
Finally,it should be noticed that,based on the thorough understanding of the linear transient mechanism,the work in this paper can be further extended to the study of the optimal control on the Poiseuille-Rayleigh-Bénard flows with the Soret effect. This will be our future research object.
| [1] | Cross, M., C. and Hohenberg, & P., C Pattern formation outside of equilibrium. Reviews of Modern Physics, 65, 851-1112 (1993) |
| [2] | Ju, ng, C, ., Lücke, M, ., and, Büchel, & P Influence of through-flow on linear pattern formation properties in binary mixture convection. Physical Review E, 54, 1510-1529 (1996) |
| [3] | Büchel, P., and Lücke, & M Influence of throughflow on binary fluid convection. Physical Review E, 61, 3793-3810 (2000) |
| [4] | Büchel, P., and Lücke, & M Localized perturbations in binary fluid convection with and without throughflow. Physical Review E, 63, 63, 026307 (2001) |
| [5] | Ju, ng, D., and Lücke, & M Traveling wave fronts and localized traveling wave convection in binary fluid mixtures. Physical Review E, 72, 72, 026307 (2005) |
| [6] | H, u, J, ., Benhadid, H, ., and, Henry, & D Linear stability analysis of Poiseuille-Rayleigh-Bénard flows in binary fluids with Soret effect. Physics of Fluids, 19, 19, 034101 (2007) |
| [7] | Butler, K., M. and Farrell, & B., F Three-dimensional optimal perturbations in viscous shear flow. Physics of Fluids, 4, 1637-1650 (1992) |
| [8] | Trefethen, L., N., Trefethen, A., E., Reddy, S., C., and, Driscoll, & T., A Hydrodynamic stability without eigenvalues. Science, 261, 578-584 (1993) |
| [9] | Reddy, S., C., Schmid, P., J., and, Henningson, & D., S Pseudospectra of the Orr-Sommerfeld operator. SIAM Journal on Applied Mathematics, 53, 15-47 (1993) |
| [10] | Reddy, S., C. and Henningson, & D., S Energy growth in viscous channel flow. Journal of Fluid Mechanics, 252, 209-238 (1993) |
| [11] | Schmid, P. J. and Henningson, D. S. Stability and Transition in Shear Flows, Springer-Verlag, New York ,2001 |
| [12] | Jerome, J., J. S., Chomaz, J., M., and, Huerre, & P Transient growth in Rayleigh-Bénard Poiseuille/Couette convection. Physics of Fluids, 24, 044103 (2012) |
| [13] | Canuto, C., Hussaini, M., Quarteroni, A., and Zang, T. Spectral Methods in Fluid Dynamics, Springer-Verlag, Berlin ,1988 |
 2016, Vol. 37
2016, Vol. 37
















