Shanghai University
Article Information
- P. RANA, M.J. UDDIN, Y. GUPTA, A.I.M. ISMAIL
- Two-component modeling for non-Newtonian nanofluid slip flow and heat transfer over sheet: Lie group approach
- Applied Mathematics and Mechanics (English Edition), 2016, 37(10): 1325-1340.
- http://dx.doi.org/10.1007/s10483-016-2140-9
Article History
- Received Mar. 17, 2016
- Revised Jun. 1, 2016
2. School of Mathematical Sciences, Universiti Sains Malaysia, Penang 11800, Malaysia;
3. Department of Mathematics, American International University-Bangladesh, Dhaka 1213, Bangladesh
The behavior of nanofluids[1-4] in various heat transfer processes of different engineering, industrial[5], and biomedical[6] applications led us to rethink the development of appropriate mathematical models. The two-component nanofluid model based on seven slip mechanisms suggested by Buongiorno[7] has attracted attention among various researchers and highlighted the importance of Brownian motion of nanoparticle and thermophoretic velocity due to temperature gradient. The problems of flow and heat transfer over stretching[8] and shrinking[9-11] sheet due to their various practical applications in plastic and wire industries, paper technology, polymer engineering, and polyethylene industries have been studied by many researchers. Khan and Pop[12] and Rana and Bhargava[13] extended these problems to nanofluid flow and heat transfer with linear and nonlinear stretching models, respectively. Kuznetsov and Nield[14] studied natural convective boundary layer flow of a nanofluid past a vertical plate. The steady state problems on nanofluid have also been extended to magneto-hydrodynamics[15-17], unsteady solution[16, 18-20], and non-Newtonian nanofluids[17, 21-24] by various scientists and researchers.
In recent studies, many authors have found multiple solutions for different flow models. Earlier, Merkin[25], Weidman et al.[26], and Harris et al.[27] found the two solutions in their respective studies. Stability analysis has been used on the basis of eigenvalues which predict physically realizable solutions. If the minimum eigenvalue is positive, then the solution is stable or physically possible, otherwise it is unstable. Moreover, the critical values calculated in these analyses tell us the existence of second solution. In recent studies of nanofluids, many authors have already found multiple solutions. Bachok et al.[28] studied stagnation point nanofluid flow over the stretching/shrinking sheet using a single component based nanofluid transport model. They concluded that the critical values for the shrinking sheet ($\varepsilon \approx -1.246 5$) remain invariant with the inclusion of Cu, Al$_{2}$O$_{3}$, and TiO$_{2}$ nanoparticles. Later, the same authors extended their work for the exponentially stretching/shrinking sheet[29]. Zaimi et al.[30-31] studied the above problem in nanofluid using two-component Buongiorno' model both for linear and nonlinear stretching/shrinking sheets. The problem of bio-convection with gyrotactic micro-organisms in nanofluids was also studied by the same authors[32]. Dhanai et al.[17] extended the problem of Zaimi et al.[31] using magnetohydrodynamic boundary layer flow and viscous dissipation effect. Later, Dhanai et al.[23] extended the work to non-Newtonian power-law fluid under slip conditions and heat source/sink and found the critical value of power-law \linebreak index.
Recently, several authors introduced the existence of spin of nanoparticle which led them to extend the two-component nanofluid model on the basis of Eringen theory[33-34] of micro-rotation which could potentially explain theoretical and experimental results. Gorla and Kuma- ri[35] investigated the Eringen theory based micropolar nanofluid model for nonlinear stretching sheet. Hussain et al.[36] implemented the different correlations for silver and copper nanoparticles considering the homogenous model using the Eringen micropolar model. Under these assumpti-ons[37-39], we extend the paper of micropolar fluid by Yacob and Ishak[40] to the nanofluid model. The passively controlled boundary conditions on nanoparticle which is coupled with temperature proposed by Kuznetsov and Nield[41] are also taken in consideration so that we can have a more realistic model. The main focus is on finding the critical values for suction and shrinking parameters by taking multiple-slip effects[42-43] and, further, the stability analysis is also performed. To the authors' best knowledge, this analysis has not been done before.
2 Mathematical formulationConsider the flow of viscous incompressible micropolar nanofluid in the region $\overline{y}>0$ driven by a shrinking sheet of uniform temperature $T_{\mathrm w} $. The sheet velocity is assumed to vary linearly with the distance $\overline{x}$ from the fixed point on the sheet, i.e., $U_{\mathrm w} (\overline{x})=a_{1}\chi\overline{x}$, where $a_{1} $ is a positive constant. The flow model for the present problem is described in Fig. 1. The simplified two-dimensional equations governing the flow in the boundary layer of a steady, laminar, and incompressible micropolar nanofluid are[7, 44]

|
| Fig. 1 Physical model and coordinate system |
|
|
The boundary conditions for the model obtained from Karniadakis et al.[45] are given as
Here, $\overline{u}$ and $\overline{v}$ are the velocity components along the $\overline{x}$- and $\overline{y}$-axes, $\overline{N}$ is the micro-rotation/ angular velocity, $\rho $ is the fluid density, $U_{\mathrm w}$ and $T_{\mathrm w}$ are the velocity and the temperature of the sheet, respectively, $T_\infty$ is the ambient temperature (less than $T_{\mathrm w}$), $\nu $ is the kinematic viscosity, $T$ is the temperature, $C$ is the nanoparticle volume fraction concentration, $\mu $ is the dynamic viscosity, $j$ is the microinertia density, $\alpha $ is the thermal diffusivity, m is a constant, $\gamma $ is the micropolar spin gradient viscosity, $D_{1} $ is the thermal slip factor, $N_{1} $ is the hydrodynamic slip factor, $\kappa $ is the vortex viscosity, $D_{\mathrm B} $ is the Brownian diffusion coefficient, $D_{\mathrm T} $ is the thermophoretic diffusion coefficient, $\tau =\frac{(\rho c)_{\mathrm p} }{(\rho c)_{\mathrm f} } $ is the ratio of heat capacity of the nanoparticle and fluid, $(\rho c)_{\mathrm f} $ is the heat effective heat capacity of the fluid, and $(\rho c)_{\mathrm p} $ is the effective heat capacity of the nanoparticle material. Further, $V_{\mathrm w} $ is the mass flux through the permeable sheet with $V_{\mathrm w} <0$ for suction and $V_{\mathrm w}>0$ for injection. We notice that $m$ is a constant such that $0\le m\le 1$. Following Ahmadi[46], we assume that $\gamma $ is given by
2.1 Boundary layer equations in dimensionless formWe consider the steady state flow and introducing the following dimensionless variables:
and hence introducing the dimensionless stream function $\psi$ defined by $u=\frac{\partial \psi }{\partial y}$ and $v=-\frac{\partial \psi }{\partial x} $ into Eqs. (2)-(5) , we derive
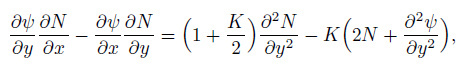 (10)
(10) 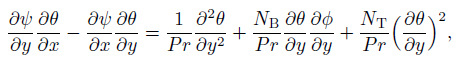 (11)
(11) 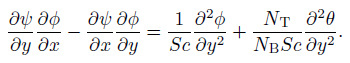 (12)
(12) The boundary conditions become
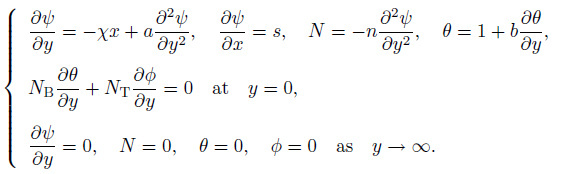 (13)
(13) The dimensionless parameters defined in Eqs. (9) -(13) are as follows. $\chi$ is the shrinking parameter, $K=\frac{\kappa }{\mu } $ is the micropolar parameter, $Pr =\frac{\nu }{\alpha } $ is the Prandtl number, $a=N_{1} \sqrt{a_{1} \nu } $ is the velocity slip parameter, $b=D_{1} \sqrt{\frac{a_{1} }{\nu } } $ is the thermal slip, $N_{\mathrm B}=\frac{\tau D_{\mathrm B} \Delta C}{\alpha } $ is the Brownian motion parameter, $N_{\mathrm T}=\frac{\tau D_{\rm T} \Delta T}{\alpha } $ is the thermophoresis parameter, $Sc=\frac{\nu }{D_{\mathrm B} } $ is the Schmidt number, and $s=-\frac{V_{\mathrm w} }{\sqrt{a_{1} \nu } } $ is the suction/injection parameter.
2.2 Search for similarity transformations using Lie group analysisThe solution of the system of partial differential equations (9) -(12) with the boundary conditions (13) is extremely difficult and computationally expensive. Hence, we transform them into a corresponding ordinary differential equations system using the scaling group of transformations. We define the scaling group of transformations as follows[47]:
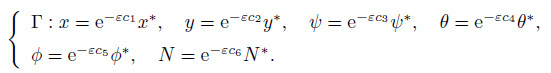 (14)
(14) Here, $\varepsilon$ is the parameter of the group $\Gamma $, and $c_{i} (i=1, 2, \cdots, 6) $ are arbitrary real numbers not all zero, simultaneously. Equations (9) -(12) will remain invariant under the group of transformations in Eq. (14) if $c_i$ for different values of $i$ can be related as
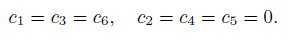 (15)
(15) Note that $y^{*} =y, ~\theta ^{*} =\theta , ~\phi ^{*} =\phi, $ i.e., $y, ~\theta$, and $\phi$ are invariants. Let us denote them by $\eta =y, ~ \theta =\theta (\eta )$, and $\phi =\phi(\eta)$. The characteristic equation is
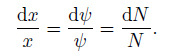 (16)
(16) Solving Eq. (16) , we obtain
Hence, the similarity transformations are
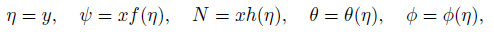 (17)
(17) where $\eta $ is the similarity independent variable, $f(\eta )$ is the dimensionless velocity function, and $h(\eta)$ is the dimensionless angular velocity.
2.3 Similarity equationsUsing Eq. (17) , from Eqs. (9) -(12) , we have
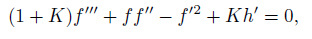 (18)
(18) 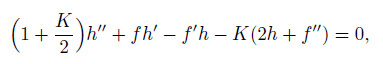 (19)
(19) 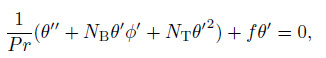 (20)
(20) 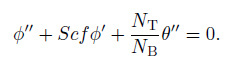 (21)
(21) The boundary conditions (13) now become
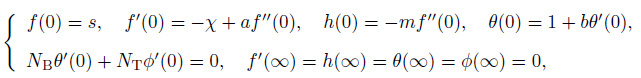 (22)
(22) where primes denote ordinary differentiation with respect to $\eta $.
2.4 Quantities of engineering interestThe physical quantities for this study are the dimensionless friction factor and the rate of heat and mass transfer. The non-dimensional friction factor is defined as
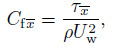 (23)
(23) where
Using Eqs. (8) and (17) in Eq. (23) , we deduce
We finally obtain
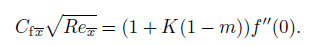 (24)
(24) The non-dimensional Nusselt number $Nu_{\overline{x}} $ and the Sherwood number $Sh_{\overline{x}} $ are defined as
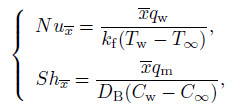 (25)
(25) where $q_{\mathrm w} $ and $q_{\mathrm m} $ are the wall heat and mass flux due to combined effect of Brownian motion and thermophoresis, respectively. Thus, $q_{\mathrm w} $ and $q_{\mathrm m} $ are described as
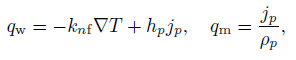 (26)
(26) where
Using Eqs. (8) and (17) in Eqs. (25) and (26) , we have
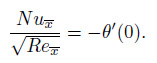 (27)
(27) In the above expressions, $Re_{\overline{x}} =\frac{U_{\mathrm w} \overline{x}}{\nu } $ is the local Reynolds number. The Sherwood number is calculated as zero due to the revised boundary condition
3 Flow stability analysisTo investigate the stability of the both branches (upper and lower), we consider the unsteady governing equations (1) -(5) . We introduce the following transformations:
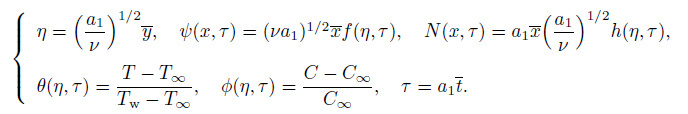 (28)
(28) Using Eq. (28) , the system of Eqs. (1) -(5) is reduced into the following dimensionless partial differential equations:
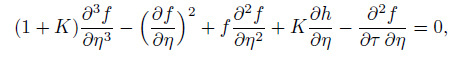 (29)
(29) 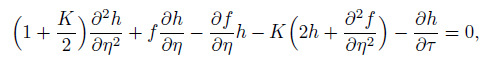 (30)
(30) 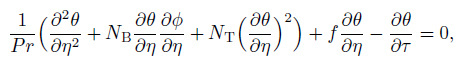 (31)
(31) 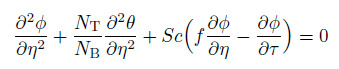 (32)
(32) subject to the boundary conditions
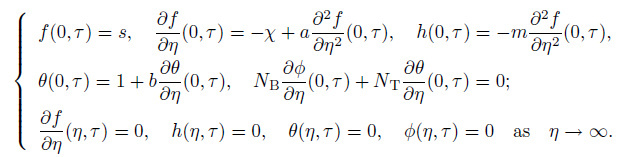 (33)
(33) To test the stability of the steady state solutions $f(\eta )=f_{0} (\eta)$, $h(\eta)=h_{0} (\eta)$, $\theta(\eta)=\theta _{0} (\eta )$, and $\phi (\eta )=\phi _{0} (\eta)$ satisfying the given boundary value problem, we have to consider[23, 25-27]
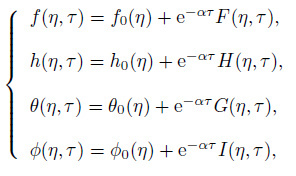 (34)
(34) where $\alpha $ is an unknown eigenvalue parameter, and $F(\eta , \tau )$, $H(\eta , \tau )$, $G(\eta , \tau )$, and $I(\eta , \tau )$ are small relative to $f_{0} (\eta )$, $h_{0} (\eta )$, $\theta _{0} (\eta )$, and $\phi _{0} (\eta )$, respectively. We obtain the following linearized problem:
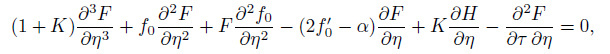 (35)
(35) 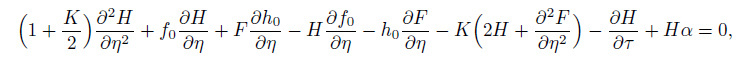 (36)
(36) 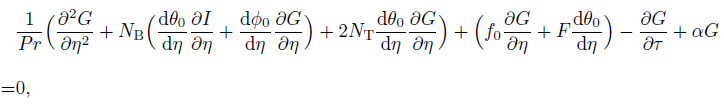 (37)
(37) 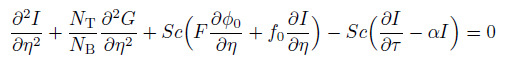 (38)
(38) along with the boundary conditions
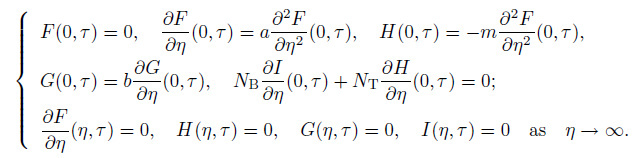 (39)
(39) The stability of the steady state solutions $f(\eta)=f_{0} (\eta )$, $h(\eta)=h_{0} (\eta)$, $\theta(\eta)=\theta _{0}(\eta)$, and $\phi (\eta)=\phi _{0} (\eta)$ can be done by setting $\tau =0$ and $F=F_{0} (\eta )$, $G=G_{0} (\eta )$, $H=H_{0} (\eta )$, and $I=I_{0} (\eta )$. The following linear eigenvalue problems are obtained:
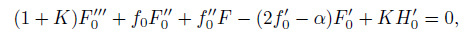 (40)
(40) 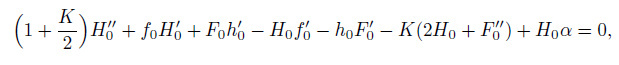 (41)
(41) 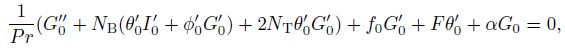 (42)
(42) 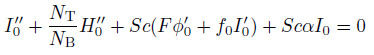 (43)
(43) with the boundary conditions
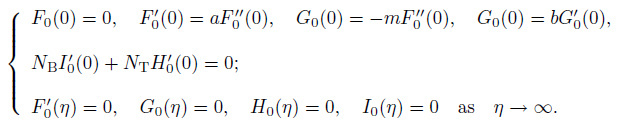 (44)
(44) The stability of physical realizable solution either first solution (solid line) or second solution (dashed line) for the steady flow $f_{0}(\eta )$, $h_{0}(\eta)$, $\theta _{0}(\eta)$, and $\phi _{0} (\eta)$ is determined by the smallest eigenvalue $\alpha $ for fixed values of governing parameters. The range of possible eigenvalues can be obtained by relaxing a suitable boundary condition on $F_{0} (\eta)$, $G_{0} (\eta )$, $H_{0}(\eta)$, or $I_{0} (\eta)$. For the present problem, we relax the condition that $F'_{0}(\eta)\to 0$ as $\eta \to \infty $. Hence, for a fixed value of $\alpha $, we solve the final system (40) -(44) with the new boundary condition $F"_{0}=1$.
4 Results and discussionIn the present analysis, the system of ordinary differential equations (18) -(21) with the boundary conditions (22) is solved using the RKF45 method[17, 19, 23, 43, 48-49], and the results are validated with the ode solver in MATLAB. The calculations throughout the paper are carried out with the default set of governing parameter as $K$=1, $m$ = 0.5, $Pr$ = 6.2, $Sc$ = 10, $s$ = 3.0, $\chi =-1$, $N_{\mathrm B}=N_{\mathrm T}$ = 0.5, $a=b$ = 0.5, unless otherwise stated. The two solution branches are captured for different sets of controlling parameters, and the critical values ($s_{\mathrm c}, \chi _{\mathrm c} $) are determined for the micropolar nanofluid. The critical value for any parameter tells us the existence of no solution ($-\infty <s_{\mathrm c} , \chi _{\mathrm c} $), unique solution ($s_{\mathrm c} , \chi _{\mathrm c} $), and multiple solutions ($s_{\mathrm c}, \chi _{\mathrm c}>\infty $) in its domain. The linear regression analysis is also carried out for finding the overall impact of dominant parameters on the reduced Nusselt number for both no-slip and multiple-slip conditions. Under the no-flux boundary condition as suggested by Kuznetsov and Nield[41] in their revised publications, we develop the correlations with the set of parametric values $K$=[0.1, 0.6, 1.3, 1.9], [$N_{\mathrm T}$, $N_{\mathrm B}$]=[0.1, 0.2, 0.3, 0.4, 0.5] as follows:
(i) For $a=b=0$ (no-slip)
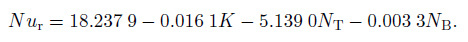 (45)
(45) (ii) For $a=b=0.5$ (multiple-slip)
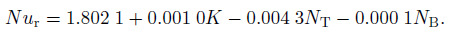 (46)
(46) The maximum errors in the above correlations for no-slip and multiple-slip are calculated to be 1.5% and 0.1%, respectively. Owing to this acceptable small error, the quadratic regression analysis is not required for the sake of brevity. It is clear from the correlations that the thermophoresis parameter is the key parameter to control the heat transfer. The behavior of the micropolar parameter is no longer the same as we go on increasing the slip parameters. With the slip parameters, the heat transfer drastically falls from 18.237 9 to 1.802 1 keeping other parameters zero. Both the Brownian motion and thermophoresis parameters are decreasing functions of the reduced Nusselt number. The contribution of Brownian motion to thermal boundary layer (which is proportional to nanoparticle concentration gradient) now tends to zero as the wall is approached, due to a passively controlled no-flux boundary condition. Moreover, the thermophoresis controls the migration of nanoparticle arises due to the temperature difference which has significant impact on the rate of heat transfer. Some of the results are presented in Table 1.
 |
The multiple solutions (two branches) for the present shrinking sheet problem containing micropolar nanofluids are evaluated numerically. The first solution (upper branch) is easy to capture, while the second solution (lower branch) requires proper choice of the maximum boundary layer thickness during numerical computations. Out of these solutions, the physical realizable solution can only be determined by stability analysis. From the solution of linear eigenvalue problem (30) -(43) with the condition (44) , we construct a table for finding the minimum eigenvalues ($\alpha $) for different values of suction parameter and slip conditions. The positive eigenvalue reveals that the solution is physically possible, whereas the negative eigenvalue corresponds to unrealizable solution. Moreover, the eigenvalues are tending to zero as we are approaching to the critical value of suction in all selected cases (see Tables 2 and 3). Thus, it strongly validates the accuracy of the solution of eigenvalue problem.
 |
 |
In Fig. 2, the skin friction is plotted against the suction parameter for $a=b=0$ and $a=b=0.5$. The solid and dashed lines correspond to upper (stable) and lower branch (unstable), respectively. According to Miklavcic and Wang[9] and Fang[11], the flow induced by the shrinking sheet can be maintained by an adequate value of suction. From the solution of flow equations, they reported that only one solution exits at s=2, but the flow will generate into two solutions when $s>2$ and no solution for $s<2$. We obtain similar results. The result obtained for $K$=0 (no-slip) strongly validates our numerical solution. As we increase the value of K from 0 to 2, the critical value for suction increases from 2.000 0 to 2.827 4. This is because of the negative contribution of rotation of nanoparticles to the velocity of fluid. There is an increase in the skin friction. However, with the consideration of both momentum and thermal slips, the critical values of suction decrease for each case of micropolar parameter ($K$=0, 1, 2) . The momentum slip at the boundary provides extra velocity which in turn decreases the skin friction.

|
| Fig. 2 Effect of micropolar parameter and critical values of suction for skin friction with both no-slip ($a=b=0$) and multiple-slip ($a=b=0.5$): first solution (solid line) and second solution (dashed line) |
|
|
Figures 3 and 4 depict the behavior of the critical value of the shrinking parameter for the skin friction and the Nusselt number, respectively. For the fixed value of suction which is taken as 3, the values of $\chi _{\mathrm c}<\chi $ are $-$2.252 0, $-$1.150 2, and $-$1.125 5 for $K$=0, 1, and 2, respectively. Beyond that, there is no solution for the given boundary value problem. With the incorporation of slip conditions, the critical values rise to $-$2.971 5, $-$1.812 5, and $-$1.300 6 which reveal the opposite behavior for the shrinking parameter as compared with the suction parameter. At $\chi =-1$ and $s=3$, we can easily interpret that for the upper branch, the skin friction first decreases and then increases with $K$, but for the lower branch, the skin friction decreases with $K$. With the implication of slip conditions, the skin friction continuously increases from $K$ = 0 to 2 for first solution. The Nusselt number is found to decrease for both no-slip and multiple-slip conditions with the increase of the particle spin (micropolar parameter).

|
| Fig. 3 Critical values of shrinking parameter with both no-slip ($a$=$b$=0) and multiple-slips ($a$=$b$=0.2) |
|
|

|
| Fig. 4 Critical values of shrinking parameter for Nusselt number with both no-slip ($a$=$b$=0) and multiple-slips ($a$=$b$=0.2) |
|
|
In Fig. 5, the velocity profile is established for different values of micropolar parameter. Both the branches upper and lower show opposite trend with the enhancement of particle rotation. The physically realizable upper branch for the velocity profile is detected to be diminishing with the increment of $K$. The slip conditions decrease the shrinking velocity at the boundary, but the pattern of velocity profile is the same as for the no-slip flow and thermal conditions. In Figs. 6-8, the velocity, temperature, and concentration profiles are analyzed under the effect of suction parameter. The upper branch slows down with the increase of suction, but the reverse effect is observed for lower branch. The increase in the suction parameter decreases the thermal boundary layer thickness for both cases. There is negligible difference for both the branches for temperature and concentration profiles. With the no-flux and no-slip conditions, the concentration first boosts up near the sheet which is higher for larger suction parameter, and later after $\eta \approx 0.05$, the concentration also tends to ambient concentration much faster for higher suction values. It should be kept in mind that the pore size is sufficiently large as compared with the nanoparticle diameter to prevent clogging of these particles and necessary surfactant should be added to avoid settling. Finally in Figs. 9(a) and 9(b), the streamlines are plotted for both solutions (upper and lower) with the default set of parameters. For both cases, the flows are symmetric about the $y$-axis. Due to high value of suction, the streamlines slightly bend towards the center for upper branch, and this impact is prominent for the case of lower branch.

|
| Fig. 5 Both upper and lower branches of velocity profile with different values of K for different slip conditions |
|
|

|
| Fig. 6 Both upper (solid) and lower (dashed) branches of velocity profile with different suction values and slip conditions |
|
|

|
| Fig. 7 Both upper (solid) and lower (dashed) branches of temperature profile with selected set of parameters |
|
|

|
| Fig. 8 Both upper (solid) and lower (dashed) branches of concentration profile with selected set of parameters |
|
|

|
| Fig. 9 Streamline plots for default set of values |
|
|
In the present framework, the multiple solutions are captured for the problem of flow over a shrinking sheet. The non-Newtonian micropolar nanofluids are utilized for the present analysis which considers the particle spin of base fluid. With the implementation of physically realistic passively controlled boundary conditions, the Brownian motion parameter becomes insignificant to heat transfer. Multiple regression analysis shows that thermophoresis is now a key parameter to heat transfer. It is found to be a decreasing function of the reduced Nusselt number. Evaluation of critical values and stability analysis for realizable solution is performed.
| [1] | Eastman, J.A., Choi, S.U.S., Li, S., Yu, W., & Thompson, L.J Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Applied Physics Letters, 78, 718-720 doi:10.1063/1.1341218 (2001) |
| [2] | Keblinski, P., Prasher, R., & Eapen, J Thermal conductance of nanofluids:is the controversy over?. Journal of Nanoparticle Research, 10, 1089-1097 doi:10.1007/s11051-007-9352-1 (2008) |
| [3] | Chen, H., Ding, Y., & Tan, C Rheological behaviour of nanofluids. New Journal of Physics, 9, 367(1-24), 9(367), 1-24 (2007) |
| [4] | Lee, J.H., Lee, S.H., Choi, C., Jang, S., & Choi, S A review of thermal conductivity data, mechanisms and models for nanofluids. International Journal of Micro-Nano Scale Transport, 1, 269-322 doi:10.1260/1759-3093.1.4.269 (2010) |
| [5] | Wong, K.V., & Leon, O Applications of nanofluids:current and future. Advances in Mechanical Engineering, 2, 2, 519659 (2010) |
| [6] | Tombcz, E., Bica, D., Hajdu, A., Ills, E., Majzik, A., & Vks, L Surfactant double layer stabilized magnetic nanofluids for biomedical application. Journal of Physics:Condensed Matter, 20, 20, 204103 doi:10.1088/0953-8984/20/20/204103 (2008) |
| [7] | Buongiorno, J Convective transport in nanofluids. Journal of Heat Transfer, 128, 240-250 doi:10.1115/1.2150834 (2006) |
| [8] | Crane, L.J Flow past a stretching plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 645-647 doi:10.1007/BF01587695 (1970) |
| [9] | Miklavcic, M., & Wang, C.Y Viscous flow due to a shrinking sheet. Quarterly of Applied Mathematics, 64, 283-290 doi:10.1090/qam/2006-64-02 (2006) |
| [10] | Wang, C.Y Stagnation flow towards a shrinking sheet. International Journal of Non-Linear Mechanics, 43, 377-382 doi:10.1016/j.ijnonlinmec.2007.12.021 (2008) |
| [11] | Fang, T., & Zhang, J Closed-form exact solutions of MHD viscous flow over a shrinking sheet. Communications in Nonlinear Science and Numerical Simulation, 14, 2853-2857 doi:10.1016/j.cnsns.2008.10.005 (2009) |
| [12] | Khan, W.A., & Pop, I Boundary layer flow of a nanofluid past a stretching sheet. International Journal of Heat and Mass Transfer, 53, 2477-2483 doi:10.1016/j.ijheatmasstransfer.2010.01.032 (2010) |
| [13] | Rana, P., & Bhargava, R Flow and heat transfer of a nanofluid over a nonlinearly stretching sheet:a numerical study. Communications in Nonlinear Science and Numerical Simulation, 17, 212-226 doi:10.1016/j.cnsns.2011.05.009 (2012) |
| [14] | Kuznetsov, A.V., & Nield, D.A Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 49, 243-247 doi:10.1016/j.ijthermalsci.2009.07.015 (2010) |
| [15] | Sheikholeslami, M., Gorji-Bandpy, M., Ganji, D.D., Rana, P., & Soleimani, S Magnetohydrodynamic free convection of Al2O3-water nanofluid considering thermophoresis and Brownian motion effects. Computers and Fluids, 94, 147-160 doi:10.1016/j.compfluid.2014.01.036 (2014) |
| [16] | Rana, P., Bhargava, R., & Bég, O.A Finite element simulation of unsteady magnetohydrodynamic transport phenomena on a stretching sheet in a rotating nanofluid. Proceedings of the Institution of Mechanical Engineers, Part N:Journal of Nanoengineering and Nanosystems, 227, 77-99 doi:10.1177/1740349912463312 (2013) |
| [17] | Dhanai, R., Rana, P., & Kumar, L Multiple solutions of MHD boundary layer flow and heat transfer behavior of nanofluids induced by a power-law stretching/shrinking permeable sheet with viscous dissipation. Powder Technology, 273, 62-70 doi:10.1016/j.powtec.2014.12.035 (2015) |
| [18] | Bachok, N., Ishak, A., & Pop, I Unsteady boundary-layer flow and heat transfer of a nanofluid over a permeable stretching/shrinking sheet. International Journal of Heat and Mass Transfer, 55, 2102-2109 doi:10.1016/j.ijheatmasstransfer.2011.12.013 (2012) |
| [19] | Malvandi, A., Hedayati, F., & Ganji, D.D Slip effects on unsteady stagnation point flow of a nanofluid over a stretching sheet. Powder Technology, 253, 377-384 doi:10.1016/j.powtec.2013.11.049 (2014) |
| [20] | Freidoonimehr, N., Rashidi, M.M., & Mahmud, S Unsteady MHD free convective flow past a permeable stretching vertical surface in a nanofluid. International Journal of Thermal Sciences, 87, 136-145 doi:10.1016/j.ijthermalsci.2014.08.009 (2015) |
| [21] | Ellahi, R The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe:analytical solutions. Applied Mathematical Modelling, 37, 1451-1467 doi:10.1016/j.apm.2012.04.004 (2013) |
| [22] | Uddin, M.J., Yusoff, N.M., Bg, O.A., & Ismail, A.I. M Lie group analysis and numerical solutions for non-Newtonian nanofluid flow in a porous medium with internal heat generation. Physica Scripta, 87, 87, 025401 doi:10.1088/0031-8949/87/02/025401 (2013) |
| [23] | Dhanai, R., Rana, P., & Kumar, L Critical values in slip flow and heat transfer analysis of nonNewtonian nanofluid utilizing heat source/sink and variable magnetic field:multiple solutions. Journal of Taiwan Institute of Chemical Engineers, 58, 155-164 doi:10.1016/j.jtice.2015.06.026 (2016) |
| [24] | Cao, L., Si, X., & Zheng, L Convection of Maxwell fluid over stretching porous surface with heat source/sink in presence of nanoparticles:Lie group analysis. Applied Mathematics and Mechanics (English Edition), 37(4), 433-442 doi:10.1007/s10483-016-2052-9 (2016) |
| [25] | Merkin, J.H On dual solutions occurring in mixed convection in a porous medium. Journal of Engineering Mathematics, 20, 171-179 doi:10.1007/BF00042775 (1986) |
| [26] | Weidman, P.D., Kubitschek, D.G., & Davis, A.M. J The effect of transpiration on selfsimilar boundary layer flow over moving surfaces. International Journal of Engineering Science, 44, 730-737 doi:10.1016/j.ijengsci.2006.04.005 (2006) |
| [27] | Harris, S.D., Ingham, D.B., & Pop, I Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium:Brinkman model with slip. Transport in Porous Media, 77, 267-285 doi:10.1007/s11242-008-9309-6 (2009) |
| [28] | Bachok, N., Ishak, A., & Pop, I Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Research Letters, 6, 1-10 (2011) |
| [29] | Bachok, N., Ishak, A., & Pop, I Boundary layer stagnation-point flow and heat transfer over an exponentially stretching/shrinking sheet in a nanofluid. International Journal of Heat and Mass Transfer, 55, 8122-8128 doi:10.1016/j.ijheatmasstransfer.2012.08.051 (2012) |
| [30] | Zaimi, K., Ishak, A., & Pop, I Flow past a permeable stretching/shrinking sheet in a nanofluid using two-phase model. PLoS One, 9, e111743, 9, e111743 doi:10.1371/journal.pone.0111743 (2014) |
| [31] | Zaimi, K., Ishak, A., & Pop, I Boundary layer flow and heat transfer over a nonlinearly permeable stretching/shrinking sheet in a nanofluid. Scientific Reports, 4, 4(4404), 1-8 (2014) |
| [32] | Zaimi, K., Ishak, A., & Pop, I Stagnation-point flow toward a stretching/shrinking sheet in a nanofluid containing both nanoparticles and gyrotactic microorganisms. Journal of Heat Transfer, 136, 136, 041705 doi:10.1115/1.4026011 (2014) |
| [33] | Eringen, A. C Simple microfluids. International Journal of Engineering Science, 2, 205-217 doi:10.1016/0020-7225(64)90005-9 (1964) |
| [34] | Eringen, A. Theory of thermomicrofluids. Journal of Mathematical Analysis and Applications, 38, 480-496 doi:10.1016/0022-247X(72)90106-0 (1972) |
| [35] | Gorla, R.S.R., & Kumari, M Mixed convection flow of a non-Newtonian nanofluid over a non-linearly stretching sheet. Journal of Nanofluids, 1, 186-195 doi:10.1166/jon.2012.1026 (2012) |
| [36] | Hussain, S.T., Nadeem, S., & Haq, R.U Model-based analysis of micropolar nanofluid flow over a stretching surface. The European Physical Journal Plus, 129, 1-10 doi:10.1140/epjp/i2014-14001-y (2014) |
| [37] | Bourantas, G.C., & Loukopoulos, V.C Modeling the natural convective flow of micropolar nanofluids. International Journal of Heat and Mass Transfer, 68, 35-41 doi:10.1016/j.ijheatmasstransfer.2013.09.006 (2014) |
| [38] | Nadeem, S., Rehman, A., Vajravelu, K., Lee, J., & Lee, C Axisymmetric stagnation flow of a micropolar nanofluid in a moving cylinder. Mathematical Problems in Engineering, 378259 (2012) |
| [39] | Rehman, A., & Nadeem, S Mixed convection heat transfer in micropolar nanofluid over a vertical slender cylinder. Chinese Physics Letters, 29, 29, 124701 doi:10.1088/0256-307X/29/12/124701 (2012) |
| [40] | Yacob, N.A., & Ishak, A Micropolar fluid flow over a shrinking sheet. Meccanica, 47, 293-299 doi:10.1007/s11012-011-9439-8 (2012) |
| [41] | Kuznetsov, A.V., & Nield, D.A Natural convective boundary-layer flow of a nanofluid past a vertical plate:a revised model. International Journal of Thermal Sciences, 77, 126-129 doi:10.1016/j.ijthermalsci.2013.10.007 (2014) |
| [42] | Khan, W.A., Uddin, M.J., & Ismail, A.I.M Effect of multiple slips and dissipation on boundary layer flow of nanofluid over a porous flat plate in porous media. Journal of Porous Media, 18, 1-14 doi:10.1615/JPorMedia.v18.i1 (2015) |
| [43] | Uddin, M.J., Bg, O.A., & Ismail, A.I.M Radiative convective nanofluid flow past a stretching/shrinking sheet with slip effects. Journal of Thermophysics and Heat Transfer, 29, 513-523 doi:10.2514/1.T4372 (2015) |
| [44] | Uddin, M.J., Kabir, M.N., & Alginahi, Y.M , Lie group analysis and numerical solution of magnetohydrodynamic free convective slip flow of micropolar fluid over a moving plate with heat transfer. Computers and Mathematics with Applications, 70, 846-856 doi:10.1016/j.camwa.2015.06.002 (2015) |
| [45] | Karniadakis, G.E.M., Beskok, A., & Gad-el-Hak, M Micro flows:fundamentals and simulation. Applied Mechanics Reviews, 55, B76, 55, B76 (2002) |
| [46] | Ahmadi, G Self-similar solution of incompressible micropolar boundary layer flow over a semiinfinite plate. International Journal of Engineering Science, 14, 639-646 doi:10.1016/0020-7225(76)90006-9 (1976) |
| [47] | Bluman, G., & Anco, S Symmetry and Integration Methods for Differential Equations, Vol. 154, Springer Science & Business Media, New York (2008) |
| [48] | Dhanai, R., Rana, P., & Kumar, L Multiple solutions in MHD flow and heat transfer of Sisko fluid containing nanoparticles migration with a convective boundary condition:critical points. The European Physical Journal Plus, 131, 142(1-14), 131(142), 1-14 (2016) |
| [49] | Dhanai, R., Rana, P., & Kumar, L MHD mixed convection nanofluid flow and heat transfer over an inclined cylinder due to velocity and thermal slip effects:Buongiorno's model. Powder Technology, 288, 140-150 doi:10.1016/j.powtec.2015.11.004 (2016) |
 2016, Vol. 37
2016, Vol. 37

















