Shanghai University
Article Information
- Yiqiang CHEN, Wenjuan YAO
- Mechanical model of round window membrane under reverse excitation
- Applied Mathematics and Mechanics (English Edition), 2016, 37(10): 1341-1348.
- http://dx.doi.org/10.1007/s10483-016-2136-9
Article History
- Received Mar. 1, 2016
- Revised Apr. 25, 2016
Conductive hearing loss is a kind of disease that is because of the congenital or acquired diseases in the external auditory canal or middle ear, which block the way that the acoustic wave transmits from external auditory canal to inner ear. The clinical application of treatment, for now, is mainly through reconstruction of different kinds of ossicular chain[1]. Since the 1990s, studies have showed that when the ossicular chain and the oval window are damaged because of lesions, in order to treat the conduction deafness, the external excitation can be directly applied to the round window, which can cause the basilar membrane to vibrate through reverse incentives[2-3]. In the early research, Nakajima et al.[4] measured differential pressures of the basilar membrane in cadaveric human temporal bones with laser vibrometry and proposed driving force equivalent calculation method which assumed that the movement of basilar membrane was equivalent under different driving forms that are the round window and the oval window. Since the coupling mechanism between the round window and the inner ear is not clear, many problems such as the size of the coupling surface and whether the soft tissue is added between the round window and the inner ear are studied, which provide the basis for implantation of the prosthesis exerted from the round window[5-11]. However, these methods all have some interference factors. In view of this, based on the success analysis of the ear structure by the analytic theory and method[12-13], a more direct and effective method, i.e., the variational principle is used to analyze the movement of round window membrane of the cochlea.
In this paper, the effect of the reverse excitation on hearing is studied from the perspective of mechanics. In the reverse excitation, the round window membrane is a key component to convert external excitation to vibration. Therefore, the mechanical model of the round window membrane is established. According to the vibration law of the sound conduction of the ear structure, the Euler equation and the corresponding complementary boundary conditions of the round window membrane are obtained by the variational principle. Combined with the Bessel function, the analytical solution of the round window membrane displacement is achieved by MATHEMATICA. Combined with clinical characteristics of the round window membrane lesion, the effect of sound transmission made by thickening of the round window membrane caused by the otitis media, shrinkage of the round window membrane area caused by otosclerosis, and hardening of the round window membrane itself is analyzed.
2 Mechanical model of round window membrane 2.1 ModelThe round window membrane model is assumed as follows:
(i) The round window membrane is homogeneous, isotropic, and in accordance with Hooke's law.
(ii) The support for the cochlear round window is hinge support.
(iii) Artificial excitation on the round window membrane acts as a uniform pressure that plays a leading role in the model.
(iv) The vibration is undamped, steady, and forced.
(v) Cochlear endolymph is an incompressible fluid.
(vi) The support of oval window to round window is equivalent to elastic support.
According to the above six points, the mechanical model of the round window membrane can be established, as shown in Fig. 1.

|
| Fig. 1 Mechanical model of round window membrane |
|
|
According to the assumption, at a certain moment $t$, the functional function $w$ is equal to $w (x, y)\times f (t)$ in a stable mode, in which $w$ is related to $w (x, y)$ and has nothing to do with $t$. $f (t)$ has nothing to do with $(x, y)$ and is related to $t$. When $t$ is fixed, $f(t)$ is constant which is remembered as $C$. $C$ can be larger than, smaller than, or equal to 1. In order to simplify the calculation, $f (t)$ is assumed to 1, and then $w=w (x, y)$. $f$ is the function. $f(t)$ means the functions of time. $w(x, y)$ means the functions of $(x, y)$. $C$ is the constant.
(i) The strain energy of the round window membrane $E_\mathrm s $ is
(ii) The elastic potential energy equation on the displacement boundary condition is
(iii) The work $q$ done by an external force is
(iv) The structural strain energy $U$ is
(v) The kinetic energy of the round window membrane $T_\mathrm {rw} $ is
(vi) The kinetic energy of fluid $T_l $ is
(vii) The structural functional $\varphi$ is
Substituting Eqs.(1)-(6) into Eq.(7) leads to
Then, $w$ takes the first-order variational,
$T$ is the total kinetic energy, $E_{ku} $ is the elastic potential energy, $w$ is the displacement of the round window membrane, $h$ is the thickness of the round window membrane, $h_\mathrm l $ is the length of the fluid, $\rho _\mathrm l $ is the density of the fluid, $\rho _\mathrm {rw} $ is the density of the round window membrane, $k_u $ is the elastic coefficient of the round window membrane, $\nu$ is Poisson's ratio, and $p$ is the sound pressure on the round window membrane at a certain moment $t$. $\omega $ is the frequency of the sound pressure, $s_\sigma $ is the area of the outer boundary, $s_u $ is the area of the inner boundary, and $D$ is the flexural stiffness that $D=\frac{Eh^3}{12(1-\nu^2)}$.
$p$ is the sound pressure on the round window membrane at a certain moment $t$ which can be expressed as
where $L_p$ is the sound pressure level (dB). The unit of $p$ is Pa. $p_0 $ is the reference acoustic pressure, which is about $2\times 10^{-5}$ Pa.
Assume that
where $F$ is the function.
Then, the Euler equation is
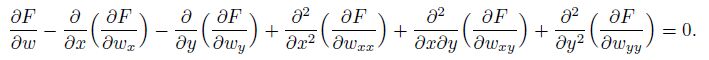 (10)
(10) Substituting Eq.(9) into Eq.(10) leads to
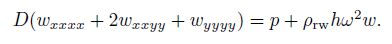 (11)
(11) The complementary boundary condition is as follows:
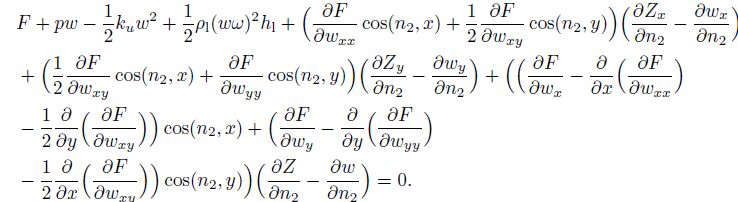 (12)
(12) The equation is held at $r=R_0 $ which is the inner boundary, where $r$ is the radius.
$n$ is the normal direction of the inner boundary, $s$ is the arc length of the inner boundary, $Z$ is the curve of the outer boundary, and $\cos(n, x)$ and $\cos(n, y)$ are the direction cosines. Other symbols are the same as Eq.(8). $R_0 $ is the inner radius.
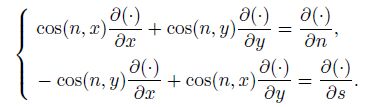 (13)
(13) According to Eq.(13), Eq.(12) can be simplified as
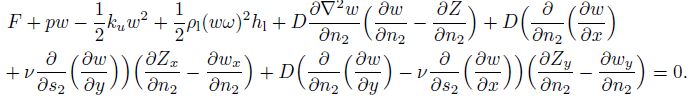 (14)
(14) According to the assumption and the simplified mechanics model, it can be seen that $\frac{\partial Z}{\partial n_2 }=0$. Since the circle has the axial symmetry, $\frac{\partial (\cdot)}{\partial s_2 }=0$. In the meantime, it is assumed that $w=w(r)$.
The boundary conditions are $w(R)=0, w(R{)}''=0$ when $r=R$ and $w(R_0 )''=0$ when $r=R_0 $.
Substitute $w=w(r)$ into Eq.(9) and then into Eq.(10) and Eq.(12). The Euler equation is simplified as
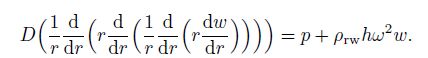 (15)
(15) The complementary boundary condition is as follows:
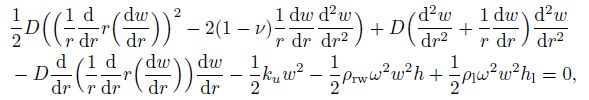 (16)
(16) where
In order to solve Eq.(15), it is assumed that
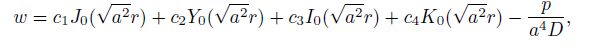 (17)
(17)
where $a=\sqrt[4]{\frac{\rho {{\omega }^{2}}h}{D}}$. J0 , Y0 , I0 , and
K0 are the Bessel functions. c1 , c2 , c3 , and c
According to the boundary condition and complementary condition, the
values of c1 , c2 , c3 , and c
Using MATHEMSTICA, Eq.(17) can be solved, and the displacement of the round window membrane mainly caused by reverse excitation can be achieved. The results are in good agreement with the experimental results, which confirms the validity of the analytic solutions. The corresponding parameters are shown in Table 1.
Figure 2 shows the variation of the displacement of round window membrane with the frequencies under 80 dB. As shown in the figure, the results from the solution have the same trend as those from the experiment[14]. At the low frequency (less than 500 Hz), the maximum displacement of round window membrane is between 34 nm-68 nm, and the average resonance frequency is at 1 818±193 Hz. The values of the displacement of the round window membrane in this paper are 53 nm-57 nm at the low frequency, and the resonance frequency is at 1 700 Hz, which are in good agreement with the experimental data. It indicates that the formula in this paper can well describe the vibration of the round window membrane.

|
| Fig. 2 Displacement of round window membrane with frequencies under 80 dB |
|
|
The acute otitis media of round window membrane thicken because of edema, inflammatory cell infiltration, and vascular proliferation in clinic. 1 time, 1.5 times and 2 times of round window membrane thickness ($h$) are compared and analyzed in Fig. 3. It can seen in Fig. 3 that the displacement of round window membrane increases first and then decreases with the increase of frequency. The maximum displacement of round window membrane decreases gradually with the increase of the thickness. It indicates that the performance of sound transmission decreases with the thickness increasing. Figure 4 shows the relationship that at 200 Hz-8 000 Hz, the difference of different thicknesses between the maximum and minimum displacements of round window membrane with the increase of the thickness. As shown in the figure, with the increase of the thickness, the difference between the maximum and the minimum displacements of round window membrane is gradually reduced. In the meantime, the difference between the maximum and minimum displacements of round window membrane changes slow as the thickness increases. It indicates that if the thickness of round window membrane increases continuously, the difference between the maximum and minimum displacements of round window membrane will be gradually reduced and be eventually close, which makes the performance of sound transmission loss gradually.

|
| Fig. 3 Different thicknesses of round window membrane with frequency under 80 dB |
|
|

|
| Fig. 4 Difference between maximum and minimum displacements at 200 Hz-8 000 Hz |
|
|
In clinic, otosclerosis is that round window niche is part or all closed because of the sclerosis. The wall of round window niche is narrowed due to erosion of the sclerosis. In this paper, changing the area of round window membrane reflects the influence made by the otosclerosis, which is roughly 0.8 times of the original area that compared with the original area, as shown in Fig. 5. It can be seen in the figure that with the decrease of round window area, the maximum displacement decreases. However, the resonance frequency is not changed and is at about 1 700 Hz. The trends of the displacements of different areas that change with frequencies are nearly the same.

|
| Fig. 5 Different areas of round window membrane with frequency under 80 dB |
|
|
Figure 6 shows the effect of round window membrane hardening on the sound transmission under 80 dB. According to the relevant literature[15-16] of ossicular ligaments hardening in clinic, 100 times of the elastic modulus larger than the normal physiological state is selected in this paper. As shown in the figure, after hardening the displacement of round window membrane does not change much with the increase of the frequency. On the whole, the trend of the displacement first increases and then decreases with a maximum at 1 700 Hz. At the same time, as the hardening of the round window membrane, the displacement of round window membrane reduces, which reveals that the performance of sound transmission decreases as the round window membrane hardens.

|
| Fig. 6 Effect of round window membrane hardening on sound transmission under 80 dB |
|
|
According to the properties of the round window membrane, six points are assumed to simplify the structure of the model, and the mechanical model of round window membrane is established. Using the variational principle, the structural vibration equation is established, and the analytical expression of the displacement in the steady state is obtained by the Bessel function. The correctness of Eq.(17) is verified by comparison with the experimental data. The use of analytical analysis can avoid the interference of environment and technical level of personnel and can evaluate the transmission performance of the round window membrane efficiently.
Combined with clinical characteristics of the round window membrane lesion, the results show that the maximum displacement of the round window membrane decreases with thickening of the round window membrane caused by the otitis media. In the meantime, with the increase of the thickness, the difference between the maximum and minimum displacements of the round window membrane is gradually reduced. Moreover, with hardening of the round window membrane and shrinkage of the membrane area, the maximum displacement of the round window membrane is reduced. It indicates that thickening of the round window membrane, shrinkage of the round window membrane area, and hardening of the round window membrane can cause the performance of the sound transmission to decrease and affect the human hearing. It reveals the effect that otitis media and otosclerosis made on hearing. Therefore, the method is simple and easy to be used. The displacement of the round window membrane can be obtained by the related parameters, which can provide a theoretical basis for the reverse excitation and clinical medicine.
| [1] | Ogale, S.B., Mabajan, S.B., Dutt, S., & Sheode, J.H Fate of middle ear implants. Auris Nasus Larynx, 24(2), 151-157 doi:10.1016/S0385-8146(96)00016-8 (1997) |
| [2] | Colletti, V., Soli, S.D., Carner, M., & Colletti, L Treatment of mixed hearing losses via implantation of a vibratory transducer on the round window. International Journal of Audiology, 45(10), 600-608 doi:10.1080/14992020600840903 (2006) |
| [3] | Voss, S.E., Rosowski, J.J., & Peake, W.T Is the pressure difference between the oval and round windows the effective acoustic stimulus for the cochlea. Journal of the Acoustical Society of America, 100(3), 1602-1616 doi:10.1121/1.416062 (1996) |
| [4] | Nakajima, H.H., Merchant, S.N., & Rosowski, J.J Performance consideration of prosthetic actuators for round-window stimulation. Hearing Research, 263(1/2), 263(1/2), 114-119 (2010) |
| [5] | Eric, L.J., Kanthaiah, K., Hyde, B.J., Jenkins, H.A., & Tollin, D.J Physiological assessment of active middle ear implant coupling to the round window in Chinchilla lanigera. Otolaryngology Head and Neck Surgery, 145(145), 641-647 (2011) |
| [6] | Tringali, S., Koka, K., Deveze, A., Holland, N.J., Jenkins, H.A., & Tollin, D.J Round window membrane implantation with an active middle ear implant:a study of the effects on the performance of round window exposure and transducer tip diameter in human cadaveric temporal bones. Audiology and Neurotology, 15(5), 291-302 doi:10.1159/000283006 (2010) |
| [7] | Schraven, S.P., Hirt, B., Gummer, A.W., Zenner, H.P., & Dalhoff, E Controlled roundwindow stimulation in human temporal bones yielding reproducible and functionally relevant stapedial responses. Hearing Research, 282(1/2), 282(1/2), 272-282 (2011) |
| [8] | Schraven, S.P., Hirt, B., Goll, E., Gummer, A.W., Zenner, H.D., & Dalhoff, E Conditions for highly efficient and reproducible round-window stimulation in humans. Audiology and Neurotology, 17(2), 133-138 doi:10.1159/000333807 (2012) |
| [9] | Wang, X., Wang, L., Zhou, J., & Hu, Y.J Finite element modelling of human auditory periphery including a feedforward amplification of the cochlea. Computer Methods in Biomechanics and Biomedical Engineering, 17(10), 1096-1107 (2012) |
| [10] | Koka, K., Holland, N.J., Lupo, J.E., Jenkins, H.A., & Tollin, D.J Electrocochleographic and mechanical assessment of round window stimulation with an active middle ear prosthesis. Hearing Research, 263(1/2), 263(1/2), 128-137 (2010) |
| [11] | Rajan, G.P., Lampacher, P., Ambett, R., Dittrich, G., Kuthubutheen, J., Wood, B., McArthur, A., & Marino, R Impact of floating mass transducer coupling and positioning in round window vibroplasty. Otology and Neurotology, 32(2), 271-277 doi:10.1097/MAO.0b013e318206fda1 (2011) |
| [12] | Li, W., Yao, W.J., Huang, X.S., & Li, X.Q Mechanical model of an artificial middle ear. Journal of Vibration and Shock, 28(3), 55-58 (2009) |
| [13] | Yao, W.J., Li, W., Huang, X.S., & Li, X.Q Constructing and solving of vibrating equation for human beings' tympanic membrane. Journal of Vibration and Shock, 27(3), 63-66 (2008) |
| [14] | Zhang, X., & Gan, R.Z Dynamic properties of human round window membrane in auditory frequencies running head:dynamic properties of round window membrane. Medical Engineering and Physics, 35(3), 310-318 doi:10.1016/j.medengphy.2012.05.003 (2013) |
| [15] | Nakajima, H.H., Ravicz, M.E., Rosowski, J.J., Peake, W.T., & Merchant, S.N Experimental and clinical studies of malleus fixation. Laryngoscope, 115, 147-154 doi:10.1097/01.mlg.0000150692.23506.b7 (2005) |
| [16] | Dai, C.K., Cheng, T., Wood, M.W., & Gan, R.Z Fixation and detachment of superior and anterior malleolar ligaments in human middle ear:experiment and modeling. Hearing Research, 230(1/2), 230(1/2), 24-33 (2007) |
 2016, Vol. 37
2016, Vol. 37
















