Shanghai University
Article Information
- M. GRYGOROWICZ, E. MAGNUCKA-BLANDZI
- Mathematical modeling for dynamic stability of sandwich beam with variable mechanical properties of core
- Applied Mathematics and Mechanics (English Edition), 2016, 37(10): 1361-1374.
- http://dx.doi.org/10.1007/s10483-016-2137-9
Article History
- Received Jan. 4, 2016
- Revised May. 5, 2016
2. Institute of Mathematics, Poznan University of Technology, Poznań 60-965, Poland
Different types of sandwich structure are well known in mechanical and civil engineering. These structures are fabricated from two thin but stiff layers named faces and a thick core. Very popular are composite structures. The most commonly used materials for the core are honeycombs, synthetic, or metal foams sometimes wood. The type of used materials for the core depend on application of whole structure. Advantages of several layer structures are lower weight, novel physical and mechanical properties, a high level of impact energy absorption, heat dissipation, electrical conductivity, and acoustic shielding. Such properties are possible to achieve through the development of manufacturing technology of porous material among other metal foams. Popularity of such structures is also evident in the rising number of publications on this topic. The authors describe the study of such structures in many directions. In the literature, one might find the statement that the first mathematician who described the low relating to mentione structures was Archimedes. He described the way how to calculate density. Considering the last century, the foundations of theory of that kind of structures after War World II were presented in the literature by Libove and Butdorf[1], Plantema[2], and Reissner[3]. They concerned on modelling of the three-layered structure taking into account the change in the shape of a normal straight to the middle surface after deformation. Manufacture, characterization, and application of cellular metals and metal foams were described by Banhart[4]. Magnucki and Szyc[5] and Magnucki et al.[6] investigated the strength, stability, and deflection of sandwich structures with an aluminum foam core. Dynamic stability of a sandwich plate was studied by Dębowski et al.[7]. Cao and Zhong[8] investigated dynamic response of an infinite beam placed on a Pasternak foundation when the system was subjected to a moving load. The similar problem was investigated by Pradhan et al.[9]. They analyzed the static and dynamic stability of an asymmetric sandwich beam with viscoelastic core lying on a variable Pasternak foundation under the action of a pulsating axial load subjected to one-dimensional thermal gradient under three different boundary conditions by the computational method. Global and local buckling of sandwich beams was investigated by Douville and Le Grognec[10], Huang and Kardomateas[11], Jasion et al.[12-13], and Jasion and Magnucki[14], Javidinejad[15], Magnucki and Stasiewicz[16], and Magnucki[17]. Grygorowicz et al.[18] described elastic buckling of a sandwich beam with variable mechanical properties of the core. They also presented analytical and finite element method (FEM) studies on buckling of sandwich beams[19].
Dynamic buckling of foam stabilized composite skin was described by Rivallant et al.[20]. Tagarielli et al.[21] investigated the dynamic response of composite sandwich beams to transverse impact. Wang et al.[22] led research on structural response of clamped sandwich beams subjected to impact loading. A similar investigation was conducted by Tan et al.[23]. They presented dynamic response of clamped sandwich beam with aluminium alloy foam core subjected to impact loading. The behavior of structural fibre composite sandwich beams made up of glass fibre composite skins and phenolic core material was investigated by Manalo[24] under three-point short beam and asymmetrical beam shear tests. Grygorowicz and Magnucka-Blandzi[25] studied stability of sandwich beams with variable properties of the core with dynamic loads. Aly et al.[26] described parametric models for design optimization and material selection of sandwich panels with the objective of weight and cost minimization subject to structural integrity constraints such as strength, stiffness, and buckling resistance. Ashjari and Khoshravan[27] developed a method for the single-objective optimization of material distribution of simply supported functionally graded isotropic plates. Brighenti[28] presented smart behavior of layered plates through the use of auxetic materials. Zingoni[29] described the group-theoretic insights on the vibration of symmetric structures in engineering. Hadji et al.[30] used the four-variable refined plate theory for the free vibration analysis of functionally graded material sandwich rectangular plates. The purpose of this paper is a mathematical description of the behavior of three-layered beam with the metal foam core dynamically loaded. The discussion is adopted variable mechanical properties of the core, which is a new approach.
The object of investigations is a three-layered beam with the metal foam core and a rectangular cross-section (see Fig. 1(a)). The beam is simply supported and axially compressed. The scheme of a considered sandwich beam, its geometry, the load, and supports are shown in Fig. 1(b). The beam is compressed by the load $F_0$. The buckling problem is considered in the elastic range. The influence of the core porosity (the parameter $k_0$) on the critical load, static and dynamic paths (if the load is changed linearly in time), and two unstable regions (if the load is pulsating) is studied. The analytical results are verified numerically with the FEM and the ANSYS system.

|
| Fig. 1 Scheme of three-layered beam |
|
|
The considered beam is three-layered. The isotropic facings are made of metal sheets, and their thickness equals $h_{\rm f}$. Young's modulus $E_{\rm f}$ and the density $\rho_{\rm f}$ of facings are constant. The isotropic but not homogeneous core is made of metal alloy foam. The density $\rho_{\rm c}$ in the middle surface of the core is ten times smaller than that in the facings. Poisson's ratio $\nu_{\rm c}$ is kept constant. The thickness of the core is $h_{\rm c}$, and the length of the beam is $L$. The mechanical properties are variable through the thickness of the core (along the $z$-direction). The biggest value of Young's modulus occurs in the middle plane of the beam (see Fig. 2) in its symmetry plane.

|
| Fig. 2 Young's modulus of core |
|
|
The minimal values occur at the top and bottom surfaces of the core. Young's modulus decreases in the direction to the facings according to the function
where $k_0$ is the parameter, and $k_0\geq 0$.
If the parameter $k_0$ equals 0, then Young's modulus of the core is constant and equals $E_{\rm c0}$. Otherwise, if this parameter increases ($0<k_0$), the mechanical properties vary. Its nonlinear characteristic is presented in Fig. 3. The density of the core is also variable through its thickness, i.e.,

|
| Fig. 3 Nonlinear characteristic of Young's modulus for different values of parameter $k_0$ |
|
|
The density of the beam core is changing with Young's modulus. However, the densities of the facings $\rho_{\rm f}$ are constant.
3 Displacements, stresses, and strainsThe stability problem of three-layered beams with variable mechanical properties of the core is studied with the use of two different hypotheses of deformation of the flat cross-section. The first one is the classical broken line hypothesis (see Fig. 4(a)). The second one is the nonlinear hypothesis (see Fig. 4(b)), which is a generalization of the classical one. Magnucka-Blandzi[31] presented detailed description of this hypothesis.

|
| Fig. 4 Scheme of deformation of beam's cross-section |
|
|
The field of displacements for each layer according to the assumed hypotheses (see Fig. 4) is formulated as follows.
(i) For the upper and lower sheet-faces $-(\frac{1}{2}+x_1)\leq\zeta\leq -\frac{1}{2}$ and $ \frac{1}{2}\leq \zeta\leq \frac{1}{2}+x_1$,
where "-" denotes the upper sheet-face and "+" denotes the lower sheet-face.
(ii) For the metal foam core $-\frac{1}{2}\leq \zeta\leq \frac{1}{2}$,
where $x$ and $z$ are the coordinates, $t$ is the time, $\zeta=z/h_{\rm c}$ is the dimensionless coordinate, $w$ is the deflection, $\psi_1(x, t)=u_{\rm f}(x, t)/h_{\rm c}$ and $\psi_2$ are the dimensionless functions, and $x_1=h_{\rm f}/h_{\rm c}$ is the dimensionless parameter.
The classical broken line hypothesis is a particular case of the above nonlinear hypothesis (when $\psi_2(x)\equiv 0$).
The relations between the strains and the displacements are nonlinear.
(i) For the upper and lower sheet-faces $-(\frac{1}{2}+x_1)\leq\zeta\leq -\frac{1}{2}$ and $\frac{1}{2}\leq \zeta\leq \frac{1}{2}+x_1$,
(ii) For the metal foam core $-\frac{1}{2}\leq \zeta\leq \frac{1}{2}$,
The stresses in the facings are defined according to Hooke's law.
(i) For the upper and lower sheet-faces $-(\frac{1}{2}+x_1)\leq\zeta\leq -\frac{1}{2}$ and $\frac{1}{2}\leq \zeta\leq \frac{1}{2}+x_1$,
(ii) For the metal foam core $-\frac{1}{2}\leq \zeta\leq \frac{1}{2}$,
4 Equations of motionOn the basis of the Hamilton principle
the system of equations of motion is derived for the considered problem. If the time is not considered, the equations of static equilibrium are obtained. The limits of integration $t_1$ and $t_2$ indicate the start and end of time.
The kinetic energy of the beam is
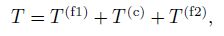 (10)
(10) where f1 and f2 denote the upper and lower facings of the sandwich beam, respectively.
The kinetic energy of the upper sheet is
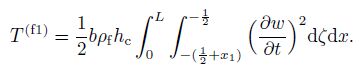 (11)
(11) The kinetic energy of the core is
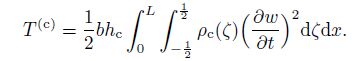 (12)
(12) The kinetic energy of the lower sheet is
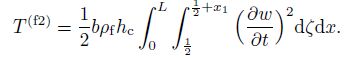 (13)
(13) The elastic strain energy of the beam is
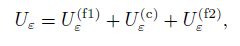 (14)
(14) where
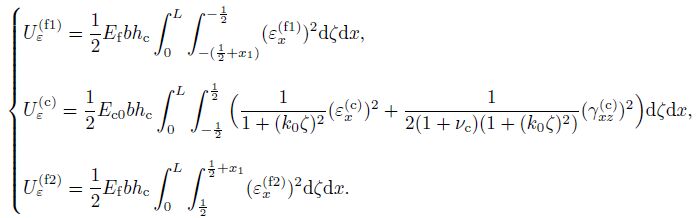 (15)
(15) Therefore, the elastic strain energy is
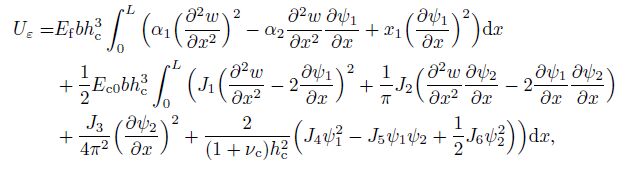 (16)
(16) where
The work of the external load is
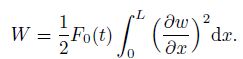 (17)
(17) Based on the principle (9), three partial differential equations are obtained as follows:
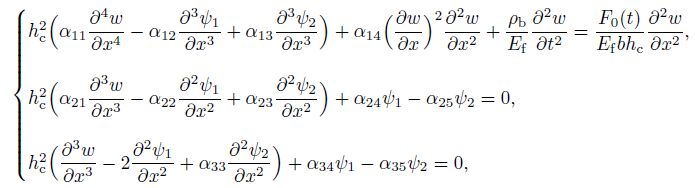 (18)
(18) where $\rho_{\rm c0}$ is the mass density in the middle surface of the beam (for $\zeta=0$), $\rho_{\rm f}$ is the mass density of the facings, and $\rho_{\rm b}=2\rho_{\rm f}x_1+\rho_{\rm c0}J_4.$
5 Static and dynamic equilibrium pathsThe system of static equilibrium is obtained, if the dependency on time in the system (18) is omitted. Then, the system can be written as follows:
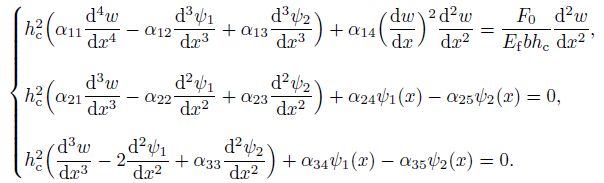 (19)
(19) The equations for unknown functions are assumed as follows:
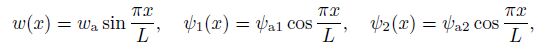 (20)
(20) which identically satisfy the boundary conditions
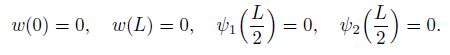 (21)
(21) The parameters $\psi_{\rm a1}$ and $\psi_{\rm a2}$ are calculated from the second and third equations of the system (19),
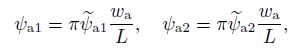 (22)
(22) where
and
After substituting the functions of $\psi_{\rm a1}$ and $\psi_{\rm a2}$ into the first equation of the system (19) and using the Bubnov-Galerkin method, the static equilibrium path is obtained,
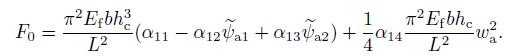 (23)
(23) The static critical load $F_{\rm cr}$ follows from the above equation (if $w_{\rm a}=0$ which means that the deflection equals zero)
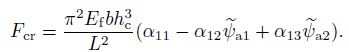 (24)
(24) Therefore, the static equilibrium path is
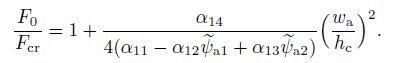 (25)
(25) If the dependency of time is taken into account for the unknown functions in Eq.(20), i.e.,
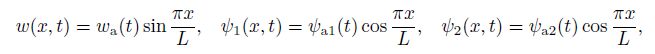 (26)
(26) then the system (18) may be reduced to one ordinary differential equation of second-order,
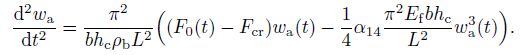 (27)
(27) For the sandwich beam subjected to the load linearly variable in time,
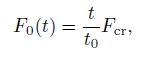 (28)
(28) where $t_0$ is the base time. The dynamic equilibrium path is obtained. Equation (27) is solved with the use of Runge-Kutta method of fourth-order.
6 Unstable regionsIn the case of linear analysis, i.e., if the relationships between the strains and the displacements are linear, the system (18) is
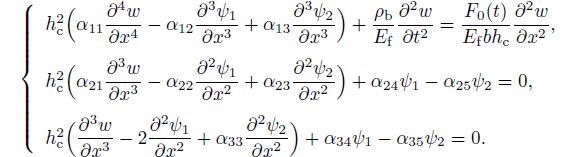 (29)
(29) In this case, the external load is assumed as the pulsating force,
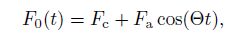 (30)
(30) where $F_{\rm c}$ is an average value of the load, $F_{\rm a}$ is an amplitude of the load, and $\Theta$ is a frequency of the load. Assuming Eq.(26) for the unknown functions, the system (29) may be reduced to the Mathieu equation,
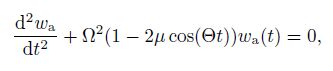 (31)
(31) where
and the angular frequency
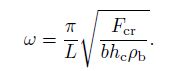 (32)
(32) Therefore, the natural frequency (in Herz) is
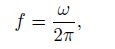 (33)
(33) and two unstable regions, according to the monograph[32], may be written as follows.
(i) The first unstable region is
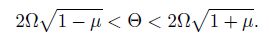 (34)
(34) (ii) The second unstable region is
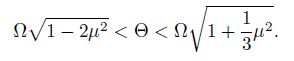 (35)
(35) Numerical calculations are performed for the family of the sandwich beams with the dimensions and mechanical properties given in Table 1.
The total hight of the beam equals 20 mm. Using the formula for the critical loads (24), their values for the family of beams are determined (see Table 2).
Moreover, to verify analytical results, the finite element model of the beam is performed. The numerical results are also given in Table 2. The numerical calculations are done with use of the ANSYS software version 14.5. Because of symmetry of the problem, only a half of the beam is considered in the FEM models with proper boundary conditions imposed on the symmetry planes (see Fig. 5). The ANSYS analysis is performed using static structural analysis and linear buckling and dynamic modal analysis. The beam is supported at the ends by displacement. Support is defined by the coordinates $x$ (along the neutral axis), $y$, and $z$. The displacement is possible only along the $x$-axis, and other coordinates are constant. The force is loaded to the edge of the beam. The facings are modeled using shell element (SHELL 181) with 4-node with six degrees of freedom at each node: translations in the $x$-, $y$-, and $z$-directions, and rotations about the $x$-, $y$-, and $z$-axes. The core is modeled using solid element (SOLID 186), a higher order three-dimensional 20-node solid element that exhibits quadratic displacement behavior. The element is defined by 20 nodes with three degrees of freedom per node: translations in the nodal $x$-, $y$-, and $z$-directions. The ANSYS FEM model of the sandwich beam consists of 20.010 rectangular elements. Bigger number of elements has no influence on the results of calculations. The buckled beam is shown in Fig. 6.

|
| Fig. 5 Finite element model of beam |
|
|

|
| Fig. 6 Buckled beam in ANSYS |
|
|
The influence of the parameter $k_0$ on the critical load is shown in Fig. 7. With the increase of the parameter $k_0$, the value of critical load decreases.

|
| Fig. 7 Critical loads |
|
|
According to Eqs.(34) and (35), two unstable regions are determined (see Fig. 8). The pulsating load is assumed as follows:

|
| Fig. 8 Unstable regions for $F_0(t)=F_{\rm cr}\big(\frac{2}{5}+\frac{3}{5}\cos(\Theta t)\big)$ |
|
|
Therefore, the maximal value of the load does not exceed the critical load. The natural frequencies are also verified numerically using the FEM. For example, for $k_0=1$, the natural frequency obtained analytically according to Eq.(33) is equal to $54.80$ Hz and numerically $51.21$ Hz.
To determine static and dynamic paths of equilibrium, the load linear variable in time is assumed as it is written in Eq.(28). These paths are presented in Fig. 9 for two different values of the parameter $k_0$.

|
| Fig. 9 Static and dynamic equilibrium paths, where continuous lines denote paths of dynamic equilibrium and dashed lines denote paths of static equilibrium |
|
|
The paths of dynamic equilibrium (continuous lines) oscillate around the paths of static equilibrium (dashed lines).
8 ConclusionsIn the design process, the structures are adopt for convenience and safety of man and not vice versa. For this reason, new solutions are sought. This is why the popularity of sandwich structure with the metal foam core increased last decades. Sandwich constructions are not only beams or plates used in mechanical engineering. They are also parts used in medicine or dentistry as spinal vertebrae or other implants. The exact mathematical description, supported by numerical and experimental studies of behavior mentioned structures dynamically loaded, is very important. Dynamic stability of a family of sandwich aluminum alloy beams with the foam core is investigated in the paper. The structure is loaded with an axial pulsating force. The variable mechanical properties of the core are taken to calculations. The deformation of flat cross-section is analyzed with use of two hypotheses: the classical broken line and the proposed nonlinear hypothesis. Strains and stresses of each layer of the beam are described. The Hamilton principle is used to derive the system of equations of motion. The bending of the beam is assumed as a function of time. The use of Galerkin method conducts to the second-order differential equation of motion for dimensionless bending. Solving this equation numerically with use of the Runge-Kutta method, the dynamic equilibrium path is obtained. Finally, the system of equations of motion is reduced to one equation known as the Mathieu equation. At last, numerical calculations for family of beams are done. Firstly, the critical load $F_\mathrm {cr}$ is calculated for selected values of $k_0$ parameter. As a reminder, this parameter is responsible for mechanical properties of the core. For the beams with a length of $1~000$ mm, the critical load changes from 5.81 kN (for $k_0=1$) to 3.16 kN (for $k_0=20$). Secondly, two unstable regions for the pulsating load $F_0(t)$ for selected $k_0$ are also calculated. It should be mentioned here that the pulsating load does not exceed the critical load. Finally, the dynamic equilibrium path is achieved in the shape of the curve oscillating around the parabola-equilibrium path for the static load.
| [1] | Libove, C. and Butdorf, S. B. A General Small-Deflection Theory for Flat Sandwich Plates, NASA TN 1526, NASA, Washington, D. C. (1948) |
| [2] | Plantema, F. J. Sandwich Construction:the Bending and Buckling of Sandwich Beams, Plates and Shells, John Wiley and Sons, New York (1966) |
| [3] | Reissner, E. Finite deflections of sandwich plates. Journal of the Aeronautical Science, 15(7), 435-440 doi:10.2514/8.11610 (1948) |
| [4] | Banhart, J. Manufacture, characterization and application of cellular metals and metal foams. Progress in Material Science, 46, 559-632 doi:10.1016/S0079-6425(00)00002-5 (2001) |
| [5] | Magnucki, K. and Szyc, W. Strength and Stability of Sandwich Beams and Plates with Aluminum Foam Core (in Polish), Poznan University of Technology Publishing House, Pozná n (2012) |
| [6] | Magnucki, K., Smyczyński, M., & Jasion, P Deflection and strength of a sandwich beam with thin binding layers between faces and a core. Archives of Mechanics, 65(4), 301-311 (2013) |
| [7] | Dębowski, D., Magnucki, K., & Malinowski, M Dynamic stability of a metal foam rectangular plate. Steel Composite Structures, 10(2), 151-168 doi:10.12989/scs.2010.10.2.151 (2010) |
| [8] | Cao, C.Y., & Zhong, Y Dynamic response of a beam on a Pasternak foundation and under a moving load. Journal of Chongqing University (English Edition), 7(4), 311-316 (2008) |
| [9] | Pradhan, M., Dash, P.R., & Pradhan, P.K Static and dynamic stability analysis of an asymmetric sandwich beam resting on a variable Pasternak foundation subjected to thermal gradient. Meccanica, 51, 725-739 (2015) |
| [10] | Douville, M. A, & Le Grognec, P. Exact analysis solutions for the local and global buckling of sandwich beam-columns under various loadings. International Journal of Solids and Structures, 50, 2597-2609 doi:10.1016/j.ijsolstr.2013.04.013 (2013) |
| [11] | Huang, H., & Kardomateas, G.A Buckling and initial post buckling behavior of sandwich beams including transverse shear. AIAA Journal, 40, 2331-2335 doi:10.2514/2.1571 (2002) |
| [12] | Jasion, P., Magnucka-Blandzi, E., Szyc, W., & Magnucki, K Global and local buckling of sandwich circular and beam-rectangular plates with metal foam core. Thin-Walled Structures, 61, 154-161 doi:10.1016/j.tws.2012.04.013 (2012) |
| [13] | Jasion, P., Magnucki, K., & Wasilewicz, P Global Buckling of Sandwich Beam-Column with Physically Nonlinear Core, Stability of structures XⅢth symposium, Department of Strength of Materials and Structures, . Technical University of Lodz, Lodź, 301-308 (2012) |
| [14] | Jasion, P., & Magnucki, K Global buckling of sandwich column with metal foam core. Journal of Sandwich Structures and Materials, 15(6), 718-732 doi:10.1177/1099636213499339 (2013) |
| [15] | Javidinejad, A Buckling of beams and columns under combined axial and horizontal loading with various axial load in application locations. Journal of Theoretical and Applied Mechanics, 42(4), 19-30 (2012) |
| [16] | Magnucki, K., & Stasiewicz, P Elastic buckling of a porous beam. Journal of Theoretical and Applied Mechanics, 42(4), 859-868 (2004) |
| [17] | Magnucki, K Strength and buckling of sandwich beams-columns (in Polish). Modelowanie Inżynierskie, 42, 249-258 (2011) |
| [18] | Grygorowicz, M., Magnucki, K., & Malinowski, M Elastic buckling of a sandwich beam with variable mechanical properties of the core. Thin-Walled Structures, 87, 127-132 doi:10.1016/j.tws.2014.11.014 (2015) |
| [19] | Grygorowicz, M. Analytical and FEM studies on buckling of sandwich beams. Proceedings of 23rd Australasian Conference on the Mechanics of Structures and Materials (ACMSM23) (ed., Smith, S. T.), Byron Bay, Australia (2014) |
| [20] | Rivallant, S., Ferrero, J.F., & Barrau, J.J Dynamic buckling of foam stabilized composite skin. Composite Structures, 72, 486-493 doi:10.1016/j.compstruct.2005.01.032 (2006) |
| [21] | Tagarielli, V.L., Deshpande, V.S., & Fleck, N.A The dynamic response of composite sandwich beams to transverse impact. International Journal of Solid and Structures, 44, 2442-2457 doi:10.1016/j.ijsolstr.2006.07.015 (2007) |
| [22] | Wang, Z., Jing, L., Ning, J., & Zhao, L The structural response of clamped sandwich beams subjected to impact loading. Composite Structures, 93, 1300-1308 doi:10.1016/j.compstruct.2010.05.011 (2011) |
| [23] | Tan, Z.H., Luo, H.H., Long, W.G., & Han, X Dynamic response of clamped sandwich beam with aluminum alloy foam core subjected to impact loading. Composites:Part B, 46, 39-45 doi:10.1016/j.compositesb.2012.10.044 (2013) |
| [24] | Manalo, A.C Behaviour of fibre composite sandwich structures under short and asymmetrical beam shear tests. Composite Structures, 99, 339-349 doi:10.1016/j.compstruct.2012.12.010 (2013) |
| [25] | Grygorowicz, M. and Magnucka-Blandzi, E. Stability of sandwich beams with variable properties of the core with dynamic loads. Proceedings of BIT's 3rd Annual World Congress of Advanced Materials-2014, World Science Press, Chongqing (2014) |
| [26] | Aly, M.F., Hamza, K.T., & Farag, M.M A materials selection procedure for sandwiched beams via parametric optimization with applications in automotive industry. Materials and Design, 56, 219-226 doi:10.1016/j.matdes.2013.10.075 (2014) |
| [27] | Ashjari, M. , & Khoshravan, M.R Mass optimization of functionally graded plate for mechanical loading in the presence of deflection and stress constraints. Composite Structures, 110, 118-132 doi:10.1016/j.compstruct.2013.11.025 (2014) |
| [28] | Brighenti, R Smart behaviour of layered plates through the use of auxetic materials. Thin-Walled Structures, 84, 432-442 doi:10.1016/j.tws.2014.07.017 (2014) |
| [29] | Zingoni, A Group-theoretic insights on the vibration of symmetric structures in engineering. Philosophical Transaction of Royal Society A, 372, 1-24 (2014) |
| [30] | Hadji, L., Atmane, H.A., Tounsi, A., Mechab, I., & Adda Bedia, E.A Free vibration of functionally graded sandwich plates using four-variable refined plate theory. Applied Mathematics and Mechanics (English Edition), 32(7), 925-942 (2011) |
| [31] | Magnucka-Blandzi, E Dynamic stability and static stress state of a sandwich beam with a metal foam core using three modified timoshenko hypotheses. Mechanics of Advanced Materials and Structures, 18(2), 147-158 doi:10.1080/15376494.2010.496065 (2011) |
| [32] | Życzkowski, M. Technical Mechanics, Strength of Construction Elements (in Polish), Publishing PWN, Warszawa (1988) |
 2016, Vol. 37
2016, Vol. 37



















