Shanghai University
Article Information
- M. MOHAMMADIMEHR, M.J. FARAHI, S. ALIMIRZAEI
- Vibration and wave propagation analysis of twisted micro-beam using strain gradient theory
- Applied Mathematics and Mechanics (English Edition), 2016, 37(10): 1375-1392.
- http://dx.doi.org/10.1007/s10483-016-2138-9
Article History
- Received Jan. 26, 2016
- Revised May. 10, 2016
Vibration and wave propagation analysis of the twisted beam structures has been an excellent research topic in many engineering fields and plays an important role in the design of turbine blades, helicopter blades, propeller blades, drill bits, and fluted cutters. These structures are used in aircraft industry and electronic packaging technology due to the complex behavior and modelling requirement of them. In practice, the twisted structures are usually modelled as Euler or Timoshenko beam. The design of micro-and nano-electro-mechanical systems (MEMS/NEMS) at micro-or nano-scale requires widespread use of micro-rods, micro-beam, and micro-plate with different complex behaviors. The important applications of twisted micro-beams are in micro-turbo machines, ultrasonic piezoelectric micro-motor design, and medical micro-devices.
Many researchers investigated the buckling and vibration analysis of twisted beam as follows.
Giannakopoulos et al.[1] illustrated a structural gradient theory of torsion, the effects of pre-twist, and the tension of pre-twisted desoxyribonucleic acid (DNA). They obtained that the complete unwinding of DNA triggers the deboning of its strands. Ho and Chen[2] studied vibrations of non-uniform rotational twisted Timoshenko beam under an axial load. At first, using the Timoshenko beam theory and Hamilton's principle, they achieved governing equations and boundary conditions and then solved these equations using the differential quadrature method (DQM). In addition, they examined the effects of the screw angle, the rotation speed, and the axial forces on the natural frequency of twisted Timoshenko beam. Leung and Fan[3] illustrated free vibrations and buckling of twisted beams under initial stress that the use of this is for designing of wind turbines and helicopter rotors blade. They examined the initial stress caused by pressure, shear force, and bending and torsional moments on the twisted Timoshenko beam frequency. The obtained equations were started using the Green strain tensor, the nonlinear part was also considered, and finally the governing equations were derived using the energy method. They concluded that the natural frequency of releasing wave increases by increasing the angle of twisted beam. Yu et al.[4] presented an effective method for curved and twisted beams with different geometric shapes. They investigated curved cantilever beam stresses and displacements under desired load and showed that the numerical results were very close to the results of the finite element method (FEM). Wang and Yu[5] achieved a modified model for the thermoelastic analysis of steady state of twisted composite beams with the initial curve. At first, they converted a three-dimensional conduction heat transfer problem into two-dimensional, and for a Timoshenko beam, they solved simultaneously these equations. Mustafa and Zhong[6] examined analytically wave propagation properties such as the cut-off frequency, the wave speed, and the wave number in a twisted micro-beam using the modified couple stress theory. They concluded that by increasing the material length scale parameter, the wave velocity increases. They also showed that the cut-off frequency depends on the material length scale parameter and the rate of twist bifurcates. Cšarek et al.[7] presented kinematically exact curved and twisted strain-based three-dimensional beam. They used the FEM to solve the equations and concluded that the convergence of discrete solution with the increasing number of finite element to the exact solution is proven. Chen[8] studied the effect of local Kelvin-Voigt damping on the natural frequencies of cantilevered twisted Timoshenko beams. He used the FEM to derive the equations of motion. Moreover, he examined the effect of twisting angle, size, and location of damper on the natural frequency of the beam. This study showed that an increase in the twist angle leads to an increase in the virtual part of first mode and reduces the virtual part of second mode. He also showed that by increasing the length of the damped part of beam, the absolute value of the real part of the frequency increases. Subrahmanyam and Rao[9] examined bending vibrations in twisted cantilever beam of variable cross. They used the Reissner method to obtain the frequency and vibrational mode shapes and obtained the effects of twists angle on modes. Chen[10] investigated the vibrations and stability of the rotation axis in Timoshenko beam twisted under an axial load. He studied the effects of thickness-to-width ratio, angle of twist, spin rate, and axial force on the buckle force and natural frequency. He found that by reducing the thickness-to-width ratio of the beam, the buckling force increases. Sinha and Turner[11] analyzed the dynamic and natural frequencies of twisted blade in a turbo machine under centrifugal force. They used the thin shell theory for blades and used the Rayleigh-Ritz method to solve governing differential equations of motion. In their study, the first five modes, including torsional and bending modes, were calculated for a wide range of blade parameters, such as the angle of twist and the ratio of beam length to its width. Their obtained results were in a good accordance with the relating studies. They concluded that as the twisting angle increases, the frequency decreases and is directly related with the angular velocity. Chen et al.[12] assessed the vibration analysis of twisted Timoshenko beams with internal Kelvin-Voigt damping. They reduced governing differential equations to second-order linear equations using the FEM. Their results showed that by increasing the damping coefficient of Kelvin-Voigt, the frequency of the imaginary part increases, while the frequency of the real part reduces. Moreover, increasing the angle of twist is always along with an increase in the imaginary part in the first mode and a decrease in the imaginary part in the second mode. Banerjee[13] analyzed the free vibration analysis of a twisted beam using the dynamic stiffness method. He achieved equations using Hamilton's principle. Then, he calculated the general solutions of equations in the case that the oscillating motion of the beam is in the harmonic mode using dynamic soft matrix achieved by applying force boundary conditions and displacement. Sabuncu and Evran[14] investigated dynamic stability of a rotating twisted Timoshenko beam with asymmetrical cross-sectional area under adverse disturbances using the FEM. They investigated the effects of shear deformation shape, rotary inertia, and shear coefficient on dynamic stability of twisted beam.
Many studies about buckling, vibration, and wave propagation of micro-and nano-structures have been done in the last decade. Mohammadimehr et al.[15] investigated the free vibration of viscoelastic double-bonded polymeric nanocomposite plate reinforced by functionally graded single-walled carbon nanotubes (FG-SWCNTs) embedded in viscoelastic foundation based on the modified strain gradient theory (MSGT) and considered various distributions of SWCNTs such as UD, FG-V, FG-X, and FG-O. Also, they obtained material properties of viscoelastic nanocomposite plates by the extended mixture rule and derived the governing equations of motion using Hamilton's principle and the sinusoidal shear deformation theory. Wang et al.[16] studied the free vibration of micro- and nano-beam models using Eringen's nonlocal theory for Timoshenko beam. The governing equations and boundary conditions were extracted using Hamilton's principle, and the analytical equations were solved for the vibrational frequencies of beams with different boundary conditions. Mohammadimehr et al.[17] studied the Reddy rectangular plate theory for biaxial buckling and bending analysis of double-coupled polymeric nanocomposite plates reinforced by functionally graded single-walled boron nitride nanotubes (FG-SWBNNTs) and FG-SWCNTs. They observed good agreement between their results and the literature result. They also investigated the effects of material length scale parameters, applied voltage, elastic foundation coefficients, aspect ratio, and van der Waals interaction on the dimensionless critical biaxial buckling load and deflection of the double-coupled nanocomposite rectangular plates. Ghorbanpour-Arani et al.[18] studied the releasing wave in a double walled boron-nitride nano-beam conveying fluid flow. The Euler-Bernoulli beam theory models were used to analyze the strain gradient theory (SGT). Their numerical results showed that the effect of nonlinear terms of motion on the phase velocity cannot be ignored in the low wave number. Narendar et al.[19] investigated wave propagation in an SWCNT under axial magnetic field using the nonlocal Euler-Bernoulli theory. They found that by increasing the magnetic force for all frequencies, the wave velocity increases. Aydogdu[20] analyzed the wave propagation of longitudinal waves in the multi-walled carbon nanotubes using the nonlocal theory. He studied the effects of van der Waals force, material length scale parameter, and radius on the wave propagation. Wang[21] analyzed wave propagation of SWCNT conveying fluid flow using the SGT. He indicated that at lower wave numbers, the fluid flow reduces phase velocity of upstream flow. Also, by increasing the flow speed, the downstream flow phase speed increases at the lower flow rate and vice versa at the higher flow rate. Liew and Wang[22] studied wave propagation in CNTs using elastic shell theories such as Love's thin cylindrical shell theory and the Cooper-Naghdi thick cylindrical shell theory. The elastic thick shell theory, in which the shear and inertia effects were considered, was developed first to investigate the wave propagations of CNTs to provide more accurate wave dispersions for higher modes. Mohammadimehr et al.[23] indicated the size-dependent effect on biaxial and shear nonlinear buckling analysis of nonlocal isotropic and orthotropic micro-plate based on surface stress and modified couple stress theories using the DQM. It is shown that the nonlinear biaxial buckling ratio decreases as the aspect ratio increases and vice versa for the buckling amplitude.
In the present research, vibration and wave propagation analysis of twisted micro-beam on Pasternak elastic foundation is studied using the SGT. Finally, the equations of motion of twisted micro-beam are obtained using the energy method and Hamilton's principle. The novelty of this article is fact that the size-dependent effects such as three material length scale parameters based on the SGT on natural frequency and wave propagation of twisted micro-beam are investigated. Basically, the use of micro in structures leads to increasing the flexural rigidity which is predicted by the SGT. Using analytical methods, the natural frequencies and speed of wave propagation of twisted micro-beam are calculated. Finally, the natural frequency, the phase speed, the cut-off frequency, and the wave number of the twisted micro-beam are affected by three parameters of the length small-scale, the speed of the twist angle, the thickness, the length of the twisted micro-beam, and the elastic foundation.
2 Governing equationsFigure 1 shows a schematic view of a uniformly twisted micro-beam with respect to the local and global coordinate axes.

|
| Fig. 1 Schematic view of uniformly twisted micro-beam as well as coordinate systems |
|
|
For the twisted micro-beam as shown in Fig. 2, the coordinate system of $O(X, Y, Z)$ is considered constant at the left end of the micro-beam that its $OZ$-axis is along the micro-beam and passes through its center, $G$ point is assumed at $Z=z$, and the local coordinate system of $G(x, y, z)$ is formed at this point, where $oz$ is in accordance with the $OZ$-axis and turns around a constant coordinate system with the angle $\varphi$. $\varphi$ is the twist angle of micro-beam at this point around the $OZ$-axis.

|
| Fig. 2 Position of local and global coordinate axes |
|
|
The displacements of $G$ point in directions of $G_x$ and $G_y $ are indicated as $u$ and $\nu$, respectively. The rotations around the axis of $G_x$ and $G_y$ are shown as $\theta_x$ and $\theta _y $. $\gamma =\frac{{\rm d}\varphi}{{\rm d}z}$ is the rate of twist angle for the twisted micro-beam. The position of the coordinate system of $\overline{G}(\overline {x}, \overline {y})$ to the coordinate system of $G(x, y)$ is shown in Fig. 3.

|
| Fig. 3 Displacement points $G$ and $\overline {G}$ of elemental length d$z$ for twisted micro-beam in local coordinate axes |
|
|
The following assumptions for this research are considered:
(i) The twisted micro-beam theory is used to obtain the displacement fields.
(ii) It is assumed that the displacement changes are constant at the $xy$-plane ($\varepsilon _{xx} =\varepsilon _{yy} =\gamma _{xy} =0)$.
(iii) The cross section of twisted micro-beam is assumed to be rectangular.
The details to obtain the longitudinal displacement ($W$) of the twisted micro-beam are given in Appendix A.
Substituting Eq.(A7c) into Eq.(A6) yields the following equation:
The longitudinal strain of $\varepsilon _{zz}$ is also calculated by derivation of $W$ in Eq.(1) with respect to $z$ as follows:
Using Eq.(A7c), Eq.(2) is simplified as follows:
The shear strains of $\gamma _{xz} $ and $\gamma _{yz}$ are also obtained as the following relations in the local coordinates:
Using Eq.(4), the shear strains of $\varepsilon _{xz} $ and $\varepsilon _{yz}$ are considered as follows:
The normal and shear strains in the $xy$-plane are calculated as follows:
2.1 Strain energy of twisted micro-beam using SGTAccording to the SGT proposed by Wang et al.[24], the strain energy $U$ for a linear elastic material is
Based on the SGT, the dilatation gradient $\gamma _i $, the deviatoric stretch gradient $\eta _{ijk}^{(1)}$, and the symmetric rotation gradient tensors $\chi _{ij}$ are defined as[24]
According to the constitutive equations for a linear isotropic elastic material, the components of stresses and higher-order stresses based on the SGT are considered as follows:
where $L_{0}$, $L_{1}$, and $L_{2 }$ are three material length scale parameters. Moreover, the parameters $p_i $, $\tau _{ijk}^{(1)} $, and $m_{ij}$ represent the higher-order stresses. Also, $\sigma _{ij} $ and $\varepsilon _{ij}$ are the normal stress and strain, respectively.
The Lame constants can be written in terms of Young's modulus $E$ and the Poisson ratio $\nu$ as follows:
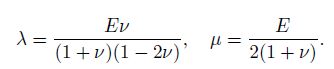 (10)
(10) Substituting Eqs.(3) and (5) into Eqs.(8) and (9), the non-zero components of the dilation gradient vector, the deviatoric stretch gradient tensor, the symmetric part of the rotation gradient tensor, and the shear and normal stresses and the higher-order stresses are obtained, as shown in Appendix B.
Substituting Eqs.(B1)-(B5) into Eq.(7), the strain energy of twisted micro-beam based on the SGT is obtained as follows:
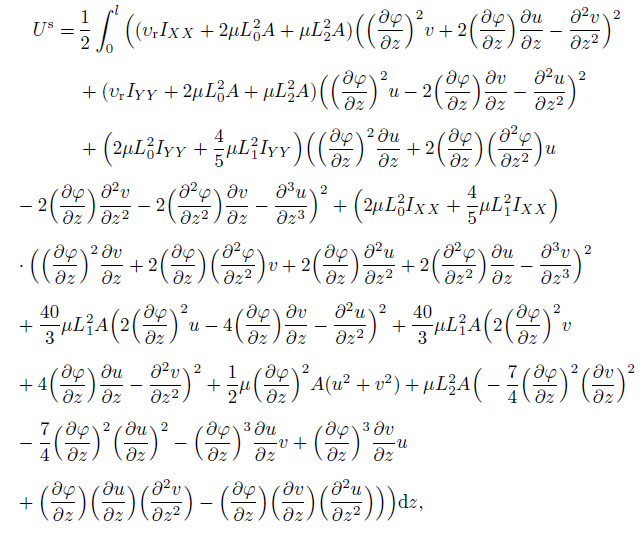 (11)
(11) where
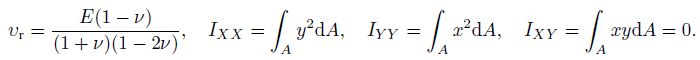 (12)
(12) Using the variational method, Eq.(11) can be written as follows:
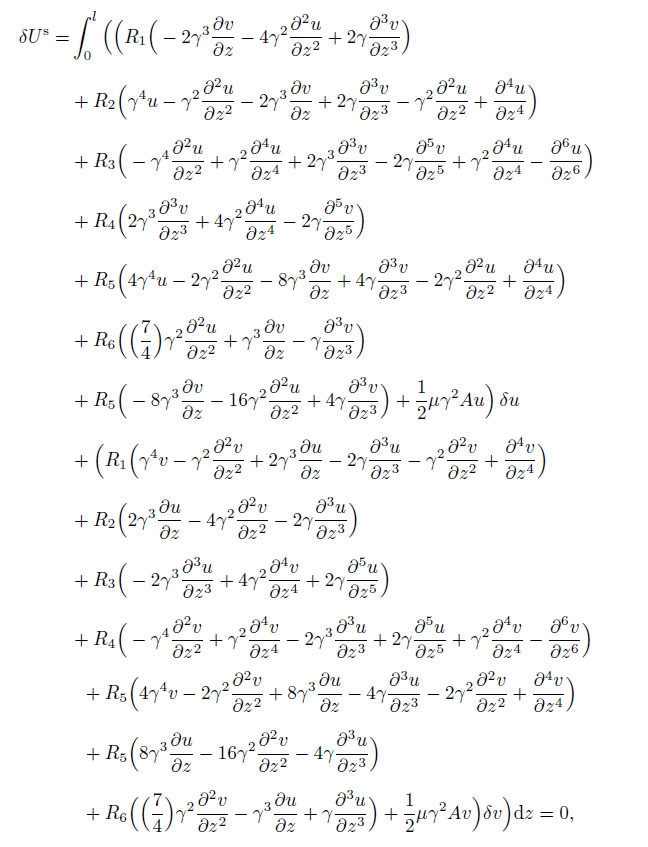 (13)
(13) where
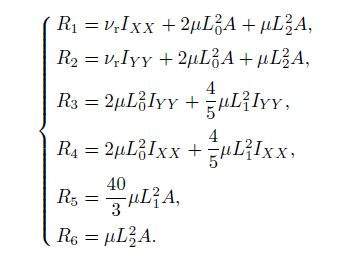 (14)
(14) The kinetic energy $T$ of the twisted micro-beam can be expressed as
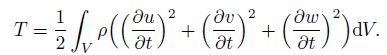 (15)
(15) The variation of the kinetic energy for the twisted micro-beam is obtained as follows:
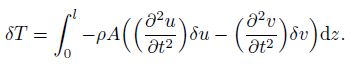 (16)
(16) The work done due to the external load such as the elastic medium for the twisted micro-beam is described by[25]
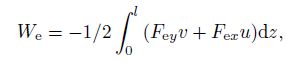 (17a)
(17a) where the forces of elastic medium in the $x$-and $y$-directions are defined as follows:
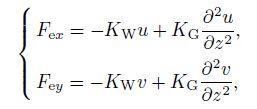 (17b)
(17b) where $K_{\rm W} $ and $K_{\rm G} $ are the spring constant of the Winkler type and the shear constant of the Pasternak type, respectively. It is noted that in this research, the elastic medium considers in two directions $x$ and $y$.
The variation of the work done due to the external load for the twisted micro-beam is taken into account as follows:
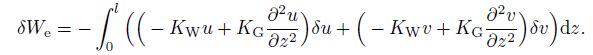 (18)
(18) To obtain the governing equations of the twisted micro-beam, Hamilton's principle is considered as follows[26]:
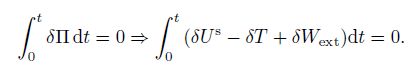 (19)
(19) Here, $U^{\rm s}$, $T$, and $W_{\rm ext} $ are the strain energy, the kinetic energy, and the virtual work done by the external forces of the twisted micro-beam. Substituting the expressions for $\delta U^{\rm s}$, $\delta T$, and $\delta W_{\rm ext}$ from Eqs.(13), (16), and (18) into Eq.(19) yields the following governing equations of the twisted micro-beam for the SGT:
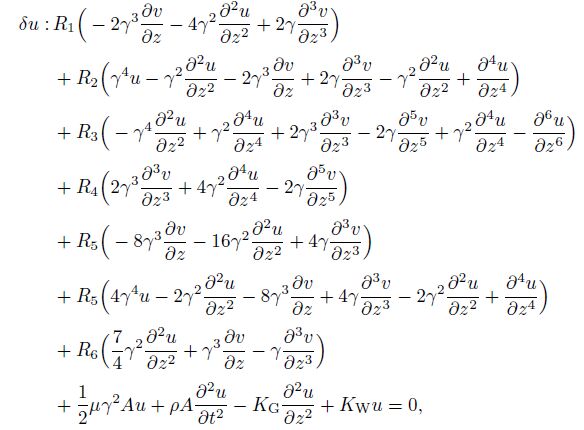 (20a)
(20a) 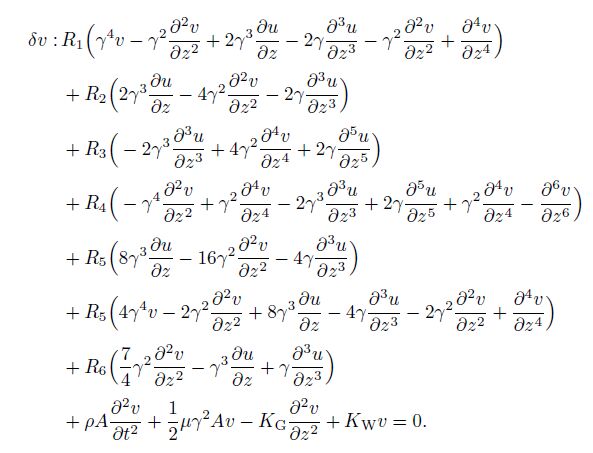 (20b)
(20b) In this section, the wave propagation and vibration analysis of the twisted micro-beam is investigated.
3.1 Wave propagation analysisThe wave propagation of the twisted micro-beam is written as follows[6]:
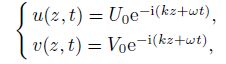 (21)
(21) where $U_0 $ and $V_0 $ are the frequency domain amplitudes of the flexural deformation of the twisted micro-beam in the $xz$-and $yz $-planes, respectively. $k$ and $\omega $ represent the wave numbers in the longitudinal direction and the frequency, respectively. Substituting Eq.(21) into Eq.(20) leads to two homogenous algebraic equations in terms of $U_0$ and $V_0$ as follows:
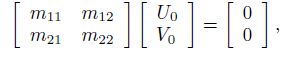 (22)
(22) where the elements of coefficient matrix are given in Appendix C with details.
To set the non-trivial solution of Eq.(22), the determinant of the coefficient matrix should be equal to zero,
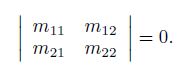 (23)
(23) Using Eq.(23), we have
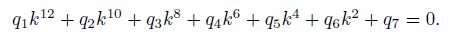 (24)
(24) The harmonic vibration of the twisted micro-beam is considered as follows:
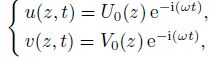 (25)
(25) where $\omega$ is the angular frequency of the twisted micro-beam[27].
By substituting Eq.(25) into Eq.(20), two algebraic equations for two cases such as the SGT can be obtained as follows:
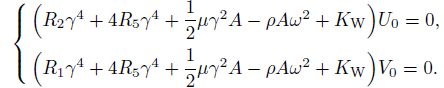 (26)
(26) The matrix form of equations can be stated as follows:
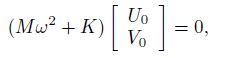 (27)
(27) where the details of the stiffness and mass matrices for the SGT can be described as follows:
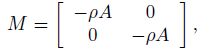 (28a)
(28a) 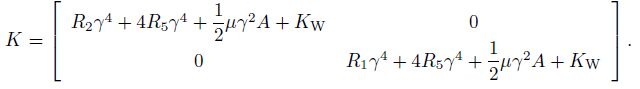 (28b)
(28b) In this section, the numerical results for the vibration and wave propagation of the twisted micro-beam on elastic foundation are presented. Mechanical properties of twisted micro-beam are given in Table 1[6].
The height of the twisted micro-beam ($h)$ is considered in the range of 17.6$\mu $m≤h≤100$\mu $m. Moreover, the width of micro-beam ($b$) and the length of micro-beam ($L)$ are considered as $2h$ and $20h$, respectively. In Fig. 4, the length scale parameters ($L_0, L_1, L_2)$ of the three materials are equal to $h/4$, while for Fig. 5, they are equal to $h/2$. In Figs. 6-13, the parameters are equal to $h/4$.

|
| Fig. 4 Phase speed ratio versus wave propagation frequency at different twist angles based on SGT |
|
|

|
| Fig. 5 Effect of material length scale parameter on phase speed based on classical theory, modified couple stress theory, and SGT |
|
|

|
| Fig. 6 Effects of thickness of twisted micro-beam on group velocity based on SGT |
|
|
In Figs. 4-6, the phase speed of the twisted micro-beam is studied. The phase speed is shown with $C_{\rm p}$ and is obtained using the equation $C_{\rm p}=\omega /k$. $\omega$ is the wave propagation frequency, and $k$ is the wave number which is inversely related with the wave length, $k=2\pi/\lambda$. In fact, the phase speed is the wave propagation speed in the environment.
Figure 4 shows the phase speed ratio versus the wave propagation frequency in different twist angles based on the SGT for $L_0 =L_1 =L_2 =h/4$. It can be seen that the phase speed in the twisted micro-beam increases by increasing the twist angle. Furthermore, by increasing the wave propagation frequency, the phase speed ratio decreases, and it remains nearly constant after the frequency of 0.6 MHz.
Figure 5 shows the effect of the material length scale parameter on the phase speed based on the classical theory ($L_0 =L_1 =L_2 =0)$, the modified couple stress theory ($L_0 =L_1 =0, L_2 =h/2)$, and the SGT ($L_0 =L_1 =L_2 =h/2)$. It is seen from Fig. 5 that the phase speed for the SGT is higher than that for the MCST and the classical theory. Three material length scale parameters increase the stiffness of twisted micro-beam. Moreover, the results of modified couple stress and classical theories are close to each other.
The group velocity is obtained from $C_{\rm g}\frac{\partial \omega }{\partial k}$, where $\omega $ is the frequency of propagation, and $k$ is the wave number. Figure 6 shows the effect of thickness of twisted micro-beam based on the SGT for $L_0=L_1=L_2 =h/4$. It is seen from Fig. 6 that by increasing the thickness of twisted micro-beam, the group velocity increases. In other words, as the thickness increases, the transfer rate of energy by wave increases.
Figure 7 illustrates the group velocity for different twist angle rates based on the SGT. The effect of twist angle rate on the group velocity is observed at lower wave propagation frequency. By increasing the propagating frequency for the propagating frequency $<0.04$, the difference of the group velocities between three cases increases, and it cannot be ignored, while for the propagating frequency $>0.04$, this result is not noticeable. Moreover, the propagating frequency is independent of the twist angle rate for higher values.

|
| Fig. 7 Effect of twist angle rate on group velocity based on SGT |
|
|
Finally, the effect of elastic foundation on the group velocity using the SGT is shown in Fig. 8. It is observed that the group velocity of twisted micro-beam increases by increasing the spring constant of Winkler type. Also, the differences of the group velocities converge at larger spring constant of Winkler type based on the SGT. Moreover, the increasing spring constant of Winkler type leads to increasing the stiffness of twisted micro-beam, and then the group velocity enhances.

|
| Fig. 8 Effect of elastic foundation on group velocity using SGT |
|
|
The lowest frequency that can be propagated in a specific condition is called the cut-off frequency. In this case, the wave number is equal to zero. Figure 9 shows the effect of the spring constant of Winkler type and the twist angle rate on the cut-off frequency based on the SGT. By increasing the twist angle rate, the cut-off frequency decreases, while vice versa for the Winkler coefficient. The elastic foundation increases the stability of system.

|
| Fig. 9 Effect of spring constant of Winkler type and twist angle rate on cut-off frequency based on SGT |
|
|
The escape frequency is the maximum frequency that can be propagated in an environment, in which the wave number has the maximum value. In Fig. 10, the effect of the material length scale parameter on the escape frequency is shown. It is observed that the escape frequency of twisted micro-beam increases by increasing the thickness of micro-beam. Moreover, the increasing thickness of twisted micro-beam leads to increasing the stiffness of micro-structure, and then the value of maximum frequency or escape frequency enhances.

|
| Fig. 10 Effect of material length scale parameter on escape frequency |
|
|
Figure 11 depicts the wave number versus the frequency of wave propagation in different thicknesses of twisted micro-beam based on the SGT. It is shown that by increasing the thickness of the twisted micro-beam, the wave number reduces. Furthermore, by increasing the frequency of wave propagation, the wave number of twisted micro-beam increases.

|
| Fig. 11 Wave number versus frequency of wave propagation in different thicknesses of twisted micro-beam based on SGT |
|
|
Figures 12, 13, and 14 show the natural frequency versus the thickness of twisted micro-beam for various rate of twist angle, Winkler spring coefficient, and three material length scale parameters of micro-structure, respectively. According to Fig. 12, with an increase in the rate of twist angle, the natural frequency of the system increases that this increase in the higher thickness of twisted micro-beam is more obvious.

|
| Fig. 12 Effect of the twist angle rate on natural frequency in various thicknesses |
|
|
In Fig. 13, with an increase in the Winkler spring coefficient, the stiffness of system increases. Thus, the natural frequency enhances. It is shown that in higher thickness of twisted micro-beam, the graphs are converged approximately. Moreover, in higher thickness, the stiffness of twisted micro-beam is higher than the stiffness of elastic medium, and then the stability of system enhances and decreases the natural frequency.

|
| Fig. 13 Effect of Winkler spring coefficient on natural frequency |
|
|
Figure 14 shows the effect of three material length scale parameters on the natural frequency of the system in different thicknesses. In this figure, three parameters of $L_0 $, $L_1$, and $L_2 $ are considered as $L_2 =L_1 =L_0 =L$. Increasing the material length scale parameter leads to increasing the stiffness of twisted micro-beam, and then the natural frequency of twisted micro-beam increases.

|
| Fig. 14 Effect of length scale parameters of three materials on natural frequency |
|
|
In this study, vibration and wave propagation analysis of the twisted micro-beam on the Pasternak foundation is presented. The displacement field and deflection of twisted micro-beam are demonstrated. The strain-displacement relations (kinematic equations) are calculated using the obtained displacement fields. The SGT is used to implement the size dependent effect at the micro-scale. Finally, the governing equations of motion for the twisted micro-beam are obtained using the energy method and Hamilton's principle. The natural frequencies and the wave propagation speed of twisted micro-beam are calculated by the analytical method. Also, the natural frequency, the phase speed, the cut-off frequency, and the wave number of twisted micro-beam are obtained by considering three material length scale parameters, the rate of twist angle, the thickness, the length of twisted micro-beam, and the elastic medium. The results of this work can be expressed as follows:
(i) The phase speed in the twisted micro-beam increases with an increase in the rate of twist angle.
(ii) The wave number is inversely related with the thickness of micro-beam. Meanwhile, it is directly related to the wave propagation frequency.
(iii) By increasing the Winkler coefficients of the twisted micro-beam, the cut-off frequency increases, while vice versa for the rate of twist angle. Also, the elastic foundation increases the stability of system.
(iv) The effect of the twist angle rate on the group velocity is presented at a lower wave propagation frequency. Also, by increasing the propagation frequency, the curves become convergent.
(v) The values of phase speed and group velocity based on the SGT are higher than those based on the modified couple stress and classical theories. However, the results of the modified couple stress and classic theories are near to each other.
(vi) Increasing the rate of twist angle leads to increasing the natural frequency which is more obvious at higher thickness.
(vii) With the increase in the Winkler spring coefficient, the stiffness of system increases. Thus, the natural frequency enhances. Moreover, in higher thickness, the stiffness of the twisted micro-beam is higher than the stiffness of the elastic medium, and then the stability of system enhances and decreases the natural frequency.
(viii) Increasing the material length scale parameter leads to increasing the stiffness of twisted micro-beam, and then the natural frequency of twisted micro-beam increases.
Appendix AThe relative displacements of $\overline {G}$ with respect to $G$ along $G_x$ and $G_y$ are written as follows[13]:
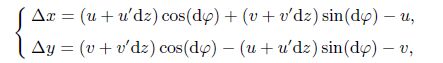 (A1)
(A1) where $u$ and $v$ are horizontal and vertical displacements of the twisted micro-beam in the local coordinates according to Fig. 3. d$\varphi $ shows the twist angle between the local and global coordinate axes. In addition, the parameters of ${u}'$ and $v'$ are given by
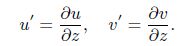 (A2)
(A2) Assuming small deformations ($\cos ({\rm d}\varphi)=1$ and $\sin ({\rm d}\varphi)={\rm d}\varphi )$ and using the equation d$\varphi =\gamma {\rm d}z$, Eq.(A1) is simplified as follows:
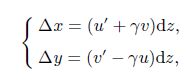 (A3)
(A3) where $\gamma $ is the rate of the twist angle with respect to the $z$-axis.
Therefore, the rotations around the axes of $G_x $ and $G_y$ at any section of the twisted micro-beam are
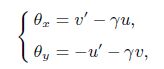 (A4)
(A4) where $\theta _x$ and $\theta _y$ represent the rotation about $x$ and $y$, respectively.
At any point of the cross section for the local coordinate $(x, y, z)$, it has displacement $(u, v, w)$. $W$ or $w$, the displacement in the $Z$-direction or in the $z$-direction, is given by
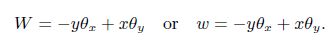 (A5)
(A5) By replacing the values of $\theta _x $ and $\theta _y$ from Eq.(A4) into Eq.(A5), we have
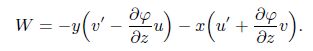 (A6)
(A6) To translate a vector including a vector displacement from the local coordinate to the global coordinate, the rotation matrix is defined as follows:
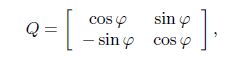 (A7a)
(A7a) 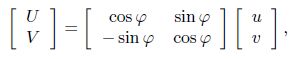 (A7b)
(A7b) 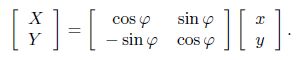 (A7c)
(A7c) Using Eq.(A7b), we have
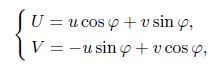 (A8)
(A8) where $U$ and $V$ are the displacements along the $X$-and $Y$-axes in the global coordinate, respectively.
Appendix BSubstituting Eqs.(3) and (5) into Eqs.(8) and (9), the non-zero components of the dilation gradient vector, the deviatoric stretch gradient tensor, the symmetric part of the rotation gradient tensor, the shear and normal stresses, and the higher-order stresses are obtained as follows:
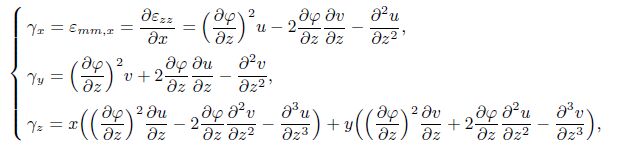 (B1)
(B1) 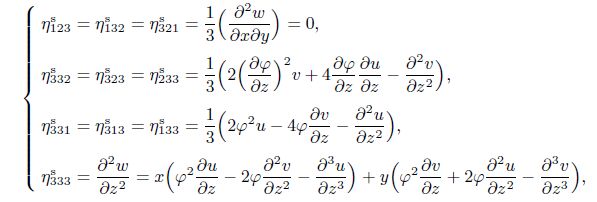 (B2)
(B2) 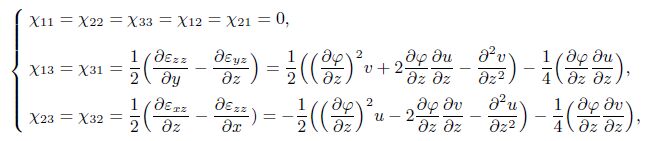 (B3)
(B3) 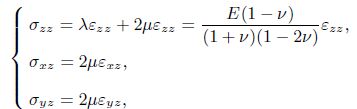 (B4)
(B4) 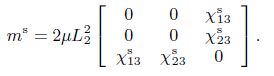 (B5)
(B5) In Eq.(22), the elements of the coefficient matrix ($m_{ij})$ are given by
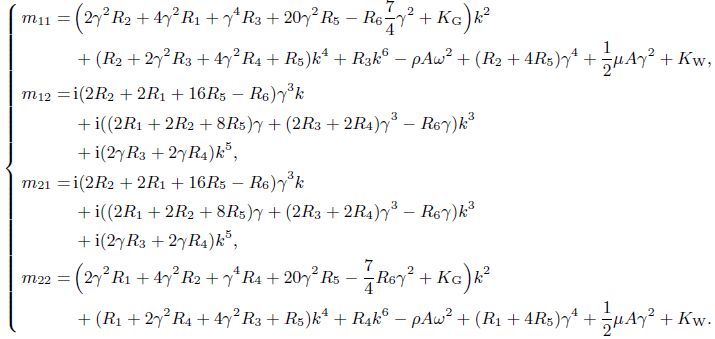 (C1)
(C1) | [1] | Giannakopoulos, A.W., Aravas, N., & Vardoulakis, P.A A structural gradient theory of torsion, the effects of pretwist, and the tension of pre-twisted DNA. International Journal of Solids and Structures, 50, 3922-3933 doi:10.1016/j.ijsolstr.2013.08.003 (2013) |
| [2] | Ho, S.H., & Chen, C.K Free transverse vibration of an axially loaded non-uniform spinning twisted Timoshenko beam using differential transform. International Journal of Mechanical Sciences, 48, 1323-1331 doi:10.1016/j.ijmecsci.2006.05.002 (2006) |
| [3] | Leung, A. Y. T, & Fan, J Natural vibration of pre-twisted shear deformable beam systems subject to multiple kinds of initial stresses. Journal of Sound and Vibration, 329, 1901-1923 doi:10.1016/j.jsv.2009.12.002 (2010) |
| [4] | Yu, A.M., Yang, X.G., & Nie, G.H Generalized coordinate for warping of naturally curved and twisted beams with general cross-sectional shapes. International Journal of Solids and Structures, 43, 2853-2876 doi:10.1016/j.ijsolstr.2005.05.045 (2006) |
| [5] | Wang, Q., & Yu, W A refined model for thermo elastic analysis of initially curved and twisted composite beams. Engineering Structures, 48, 233-244 doi:10.1016/j.engstruct.2012.09.007 (2013) |
| [6] | Mustapha, K.B., & Zhong, Z.W Wave propagation characteristics of a twisted micro scale beam. International Journal of Engineering Science, 53, 46-57 doi:10.1016/j.ijengsci.2011.12.006 (2012) |
| [7] | Cšarek, P., Saje, M., & Zupan, D. Kinematically exact curved and twisted strain-based beam. International Journal of Solids and Structures, 49, 1802-1817 doi:10.1016/j.ijsolstr.2012.03.033 (2012) |
| [8] | Chen, W.R Effect of local Kelvin-Voigt damping on eigen frequencies of cantilevered twisted Timoshenko beams. Procedia Engineering, 79, 160-165 doi:10.1016/j.proeng.2014.06.325 (2014) |
| [9] | Subrahmanyam, K.B., & Rao, J.S Coupled bending-bending vibrations of pre-twisted tapered cantilever beams treated by the Reissner method. Journal of Sound and Vibration, 82, 577-592 doi:10.1016/0022-460X(82)90408-4 (1982) |
| [10] | Chen, W.R On the vibration and stability of spinning axially loaded pre-twisted Timoshenko beams. Finite Elements in Analysis and Design, 46, 1037-1047 doi:10.1016/j.finel.2010.07.020 (2010) |
| [11] | Sinha, S.K., & Turner, K.E Natural frequencies of a pre-twisted blade in a centrifugal force field. Journal of Sound and Vibration, 330, 2655-2681 doi:10.1016/j.jsv.2010.12.017 (2011) |
| [12] | Chen, W.R., Hsin, S.W., & Chu, T.H Vibration analysis of twisted Timoshenko beams with internal Kelvin-Voigt damping. Procedia Engineering, 67, 525-532 doi:10.1016/j.proeng.2013.12.053 (2013) |
| [13] | Banerjee, J.R Free vibration analysis of a twisted beam using the dynamic stiffness method. International Journal of Solids Structures, 38, 6703-6722 doi:10.1016/S0020-7683(01)00119-6 (2001) |
| [14] | Sabuncu, M., & Evran, K The dynamic stability of a rotating pre-twisted asymmetric crosssection Timoshenko beam subjected to lateral parametric excitation. International Journal of Mechanical Sciences, 48, 878-888 doi:10.1016/j.ijmecsci.2006.01.019 (2006) |
| [15] | Mohammadimehr, M., Rousta-Navi, B., & Ghorbanpour-Arani, A Free vibration of viscoelastic double-bonded polymeric nanocomposite plates reinforced by FG-SWCNTs using MSGT, sinusoidal shear deformation theory and meshless method. Composite Structures, 131, 654-671 doi:10.1016/j.compstruct.2015.05.077 (2015) |
| [16] | Wang, C.M., Zhang, Y.Y., & He, X.Q Vibration of nonlocal Timoshenko beams. Nanotechnology, 18, 9-18 (2007) |
| [17] | Mohammadimehr, M., Rousta-Navi, B., & Ghorbanpour-Arani, A Modified strain gradient Reddy rectangular plate model for biaxial buckling and bending analysis of double-coupled piezoelectric polymeric nanocomposite reinforced by FG-SWNT. Composite Part B:Engineering, 87, 132-148 doi:10.1016/j.compositesb.2015.10.007 (2016) |
| [18] | Ghorbanpour-Arani, A., Kolahchi, R., & Vossough, H Nonlocal wave propagation in an embedded DWBNNT conveying fluid via strain gradient theory. Physica B, 407, 4281-4286 doi:10.1016/j.physb.2012.07.018 (2012) |
| [19] | Narendar, S., Gupta, S.S., & Gopalakrishnan, S Wave propagation in single-walled carbon nanotube under longitudinal magnetic field using nonlocal Euler-Bernoulli beam theory. Applied Mathematical Modelling, 36, 4529-4538 doi:10.1016/j.apm.2011.11.073 (2012) |
| [20] | Aydogdu, M Longitudinal wave propagation in multi-walled carbon nanotubes. Composite Structures, 107, 578-584 doi:10.1016/j.compstruct.2013.08.031 (2014) |
| [21] | Wang, L Wave propagation of fluid-conveying single-walled carbon nanotubes via gradient elasticity theory. Computational Materials Science, 49, 761-766 doi:10.1016/j.commatsci.2010.06.019 (2010) |
| [22] | Liew, K.M., & Wang, Q Analysis of wave propagation in carbon nanotubes via elastic shell theories. International Journal of Engineering Science, 45, 227-241 doi:10.1016/j.ijengsci.2007.04.001 (2007) |
| [23] | Mohammadimehr, M., Mohammadimehr, M.A., & Dashti, P Size-dependent effect on biaxial and shear nonlinear buckling analysis of nonlocal isotropic and orthotropic micro-plate based on surface stress and modified couple stress theories using differential quadrature method (DQM). Applied Mathematics and Mechanics (English Edition), 37(4), 529-554 (2016) |
| [24] | Wang, B., Zhou, S.H., Zhao, J., & Chen, X A size-dependent Kirchhoff micro-plate model based on strain gradient elasticity theory. European Journal of Mechanics A/Solids, 30, 517-524 doi:10.1016/j.euromechsol.2011.04.001 (2011) |
| [25] | Paliwal, D.N., Pendey, R.K., & Nath, T Free vibrations of circular cylindrical shell on Winkler and Pasternak foundations. International Journal of Pressure Vessels and Piping, 69, 79-89 doi:10.1016/0308-0161(95)00010-0 (1996) |
| [26] | Reddy J. N. Energy Principles and Variational Methods in Applied Mechanic, John Wiley and Sons, New York (2002) |
| [27] | Li, X.Y., Zhao, X., & Li, Y.H Green's functions of the forced vibration of Timoshenko beams with damping effect. Journal of Sound and Vibration, 333, 1781-1795 doi:10.1016/j.jsv.2013.11.007 (2014) |
 2016, Vol. 37
2016, Vol. 37












